福建省莆田第八中学高一上学期(人教版)数学必修一课件:1-2函数的概念(共28张PPT)
文档属性
| 名称 | 福建省莆田第八中学高一上学期(人教版)数学必修一课件:1-2函数的概念(共28张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 553.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-09-21 20:29:35 | ||
图片预览







文档简介
课件28张PPT。 1.2 函数及其表示1.2.1 函数的概念 莆田八中 数学组 魏国宝 借助大量的实际例题和视频让学生在具体问题中感受函数的概念。由于高中函数的定义是基于映射原理,但是映射却后面才学,所以在讲解定义的时候是从具体事例中体会函数概念的定义 ,切记直接从理论的高度讲解函数的定义。再结合实例进一步体会定义的准确性,把握定义中的关键词,再顺势得出函数的三要素。
本届课的重点是函数的定义和三要素中的定义域,不要拓展太多,后面一节就是函数的表示法,其实就是三要素中的对应关系,所以本节课不要把对应关系和值域也拓展开来讲。
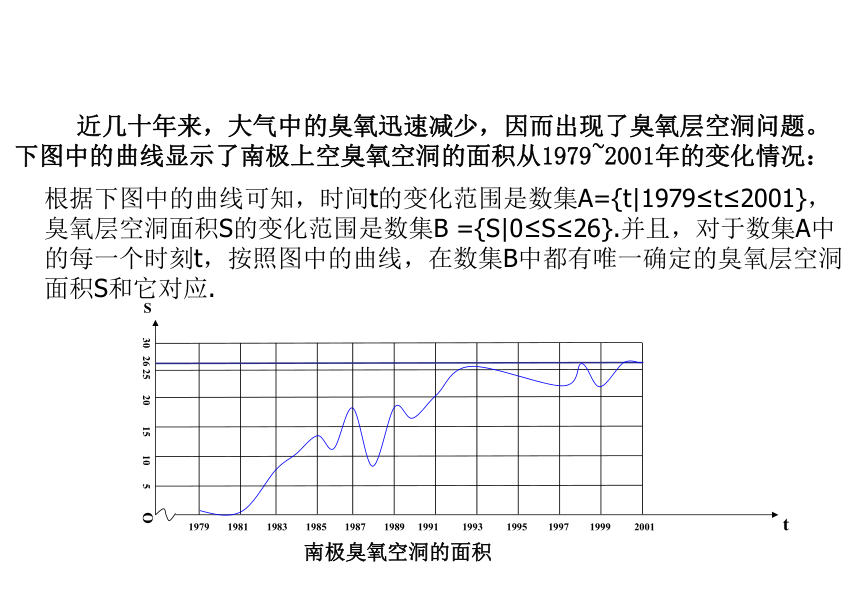
地 球 臭 氧 层 空 洞 图 片 该视频呈现了臭氧层空洞被破坏后产生的灾害 近几十年来,大气中的臭氧迅速减少,因而出现了臭氧层空洞问题。下图中的曲线显示了南极上空臭氧空洞的面积从1979~2001年的变化情况:根据下图中的曲线可知,时间t的变化范围是数集A={t|1979≤t≤2001},臭氧层空洞面积S的变化范围是数集B ={S|0≤S≤26}.并且,对于数集A中的每一个时刻t,按照图中的曲线,在数集B中都有唯一确定的臭氧层空洞面积S和它对应.1979 1981 1983 1985 1987 1989 1991 1993 1995 1997 1999 2001 t南极臭氧空洞的面积 30 26 25 20 15 10 5 OS同学们,在上例中有没体会出臭氧层空洞面积与时间之间的变化关系?再看到书本上的那几个例题,请同学们仔细阅读,思考一下这些例题中变量之间有什么共同点.目标 归纳以上实例,我们看到,实例中变量之间的关系可以描述为:
对于数集A中的每一个x,按照某种对应关系f,在数集B中都有唯一确定的y和它对应,记作 f: A→B.
设A、B ,如果按照某种对应关系f,使对于集合A中的 ,在集合B中
都有 ,那么就称
f: A→B为从集合A到集合B的一个函数,记作 y=f(x),x∈A.
函数的概念 是非空数集 任意一个数x唯一确定的数f(x)和它对应设A,B是___________,如果按照某种确定的对应关
系f,使对于集合A中的____________,在集合B中都
有_____确定的数f(x)和它对应,那么就称f:A→B为
从_____________的一个函数,记作y=f(x),x∈A.
其中,x叫做_______,x的取值范围A叫做函数的
_______;与x的值相对应的y值叫做_______,函数
值的集合{f(x)|x∈A}叫做函数的_____.非空的数集任意一个数x唯一集合A到集合B自变量定义域函数值值域思考:如果构成一个函数,需要具备几个条件?函数的三要素定义域值域对应关系练习:1.判断下列对应是否为数集A到数集B的一个函数:不是不是记C= {f(x)|x∈A},则C____B是是2. 下列图象能表示函数图象的是( )D0初中各类函数的定义域分别是什么?RRR例题展示例2 已知函数 ,求函数的定义域.
解 : 有意义的实数x的集合是{x|x≥ -3}
有意义的实数x的集合是{x|x≠2}
所以这个函数的定义域就是
求定义域的几种情况: (1)如果f(x)是整式,那么函数的定义域是实数R.
(2)如果f(x)是分式,那么函数的定义域是使分母不等于0的实数的集合.
(3)如果f(x)是二次根式,那么函数的定义域是使根号内的式子大于或等于0的实数的集合.
(4)如果f(x)是由几个部分的数学式子构成的,那么函数的定义域是使各部分式子都有意义的实数集合.(即求各集合的交集)规律总结B如果两个函数定义域相同,并且对应关系完全一致,我们就称这两个函数相等(或为同一函数)关注函数的三要素函数相等思考2:如何判断两个函数是否为同一函数?下列两个函数是否表示同一个函数?(1)(2)(3)是不是,定义域不同不是,对应关系不同【变式练习】1. 对于函数y=f(x),以下说法正确的有( )
①y是x的函数
②对于不同的x,y的值也不同
③ f(a)表示当x=a时函数f(x)的值,是一个常量
A、1个 B、2个 C、3个 D、0个B跟踪训练2.下列图象中不能作为函数的是( ).ABCDB设a,b是两个实数,而且a为_______.⒉满足不等式a_______.⒊满足不等式a≤x半闭区间,分别表示为_________________,这里的_________都叫做相应区间的端点.[a,b](a,b)[a,b),(a,b]实数a与b实数集R可以用区间表示为 读作“无穷大”,“ ”读作“负无穷大”,“ ”读作“正无穷大”。
我们可以把满足 的实数x的集合分别表示为 数轴上所有的点思考:区间可以表示数集,数集一定可以用区间表示吗?
提示:区间可以表示数集,但只能表示一些连续的实数集的子集,一些孤立的数集不一定可以用区间表示,如集合{1,2,3}不能用区间表示.例3: 把下列数集用区间表示:
(1){x|x≥-2}.
(2){x|x<0}.
(3){x|-1<x<1或2≤x<6}.
解析:(1){x|x≥-2}用区间表示为[-2,+∞).
(2){x|x<0}用区间表示为(-∞,0).
(3){x|-1<x<1或2≤x<6}用区间表示为 (-1,1)∪[2,6).练习:试用区间表示下列实数集
(1){x|2≤x<3}
(2){x|x≥15}
(3){x|x≤0}∩{x|-3 ≤x<8}
(4){x|x<-10}∪{x|3
本届课的重点是函数的定义和三要素中的定义域,不要拓展太多,后面一节就是函数的表示法,其实就是三要素中的对应关系,所以本节课不要把对应关系和值域也拓展开来讲。
地 球 臭 氧 层 空 洞 图 片 该视频呈现了臭氧层空洞被破坏后产生的灾害 近几十年来,大气中的臭氧迅速减少,因而出现了臭氧层空洞问题。下图中的曲线显示了南极上空臭氧空洞的面积从1979~2001年的变化情况:根据下图中的曲线可知,时间t的变化范围是数集A={t|1979≤t≤2001},臭氧层空洞面积S的变化范围是数集B ={S|0≤S≤26}.并且,对于数集A中的每一个时刻t,按照图中的曲线,在数集B中都有唯一确定的臭氧层空洞面积S和它对应.1979 1981 1983 1985 1987 1989 1991 1993 1995 1997 1999 2001 t南极臭氧空洞的面积 30 26 25 20 15 10 5 OS同学们,在上例中有没体会出臭氧层空洞面积与时间之间的变化关系?再看到书本上的那几个例题,请同学们仔细阅读,思考一下这些例题中变量之间有什么共同点.目标 归纳以上实例,我们看到,实例中变量之间的关系可以描述为:
对于数集A中的每一个x,按照某种对应关系f,在数集B中都有唯一确定的y和它对应,记作 f: A→B.
设A、B ,如果按照某种对应关系f,使对于集合A中的 ,在集合B中
都有 ,那么就称
f: A→B为从集合A到集合B的一个函数,记作 y=f(x),x∈A.
函数的概念 是非空数集 任意一个数x唯一确定的数f(x)和它对应设A,B是___________,如果按照某种确定的对应关
系f,使对于集合A中的____________,在集合B中都
有_____确定的数f(x)和它对应,那么就称f:A→B为
从_____________的一个函数,记作y=f(x),x∈A.
其中,x叫做_______,x的取值范围A叫做函数的
_______;与x的值相对应的y值叫做_______,函数
值的集合{f(x)|x∈A}叫做函数的_____.非空的数集任意一个数x唯一集合A到集合B自变量定义域函数值值域思考:如果构成一个函数,需要具备几个条件?函数的三要素定义域值域对应关系练习:1.判断下列对应是否为数集A到数集B的一个函数:不是不是记C= {f(x)|x∈A},则C____B是是2. 下列图象能表示函数图象的是( )D0初中各类函数的定义域分别是什么?RRR例题展示例2 已知函数 ,求函数的定义域.
解 : 有意义的实数x的集合是{x|x≥ -3}
有意义的实数x的集合是{x|x≠2}
所以这个函数的定义域就是
求定义域的几种情况: (1)如果f(x)是整式,那么函数的定义域是实数R.
(2)如果f(x)是分式,那么函数的定义域是使分母不等于0的实数的集合.
(3)如果f(x)是二次根式,那么函数的定义域是使根号内的式子大于或等于0的实数的集合.
(4)如果f(x)是由几个部分的数学式子构成的,那么函数的定义域是使各部分式子都有意义的实数集合.(即求各集合的交集)规律总结B如果两个函数定义域相同,并且对应关系完全一致,我们就称这两个函数相等(或为同一函数)关注函数的三要素函数相等思考2:如何判断两个函数是否为同一函数?下列两个函数是否表示同一个函数?(1)(2)(3)是不是,定义域不同不是,对应关系不同【变式练习】1. 对于函数y=f(x),以下说法正确的有( )
①y是x的函数
②对于不同的x,y的值也不同
③ f(a)表示当x=a时函数f(x)的值,是一个常量
A、1个 B、2个 C、3个 D、0个B跟踪训练2.下列图象中不能作为函数的是( ).ABCDB设a,b是两个实数,而且a
我们可以把满足 的实数x的集合分别表示为 数轴上所有的点思考:区间可以表示数集,数集一定可以用区间表示吗?
提示:区间可以表示数集,但只能表示一些连续的实数集的子集,一些孤立的数集不一定可以用区间表示,如集合{1,2,3}不能用区间表示.例3: 把下列数集用区间表示:
(1){x|x≥-2}.
(2){x|x<0}.
(3){x|-1<x<1或2≤x<6}.
解析:(1){x|x≥-2}用区间表示为[-2,+∞).
(2){x|x<0}用区间表示为(-∞,0).
(3){x|-1<x<1或2≤x<6}用区间表示为 (-1,1)∪[2,6).练习:试用区间表示下列实数集
(1){x|2≤x<3}
(2){x|x≥15}
(3){x|x≤0}∩{x|-3 ≤x<8}
(4){x|x<-10}∪{x|3
