福建省莆田第八中学高一上学期(人教版)数学必修一课件:1-3函数的基本性质-单调性(共27张PPT)
文档属性
| 名称 | 福建省莆田第八中学高一上学期(人教版)数学必修一课件:1-3函数的基本性质-单调性(共27张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 968.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-09-21 20:32:08 | ||
图片预览

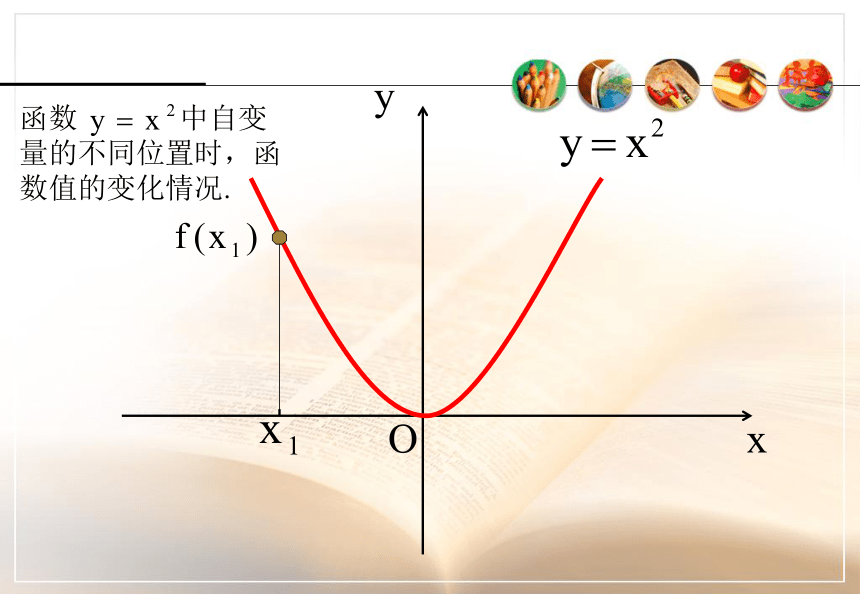
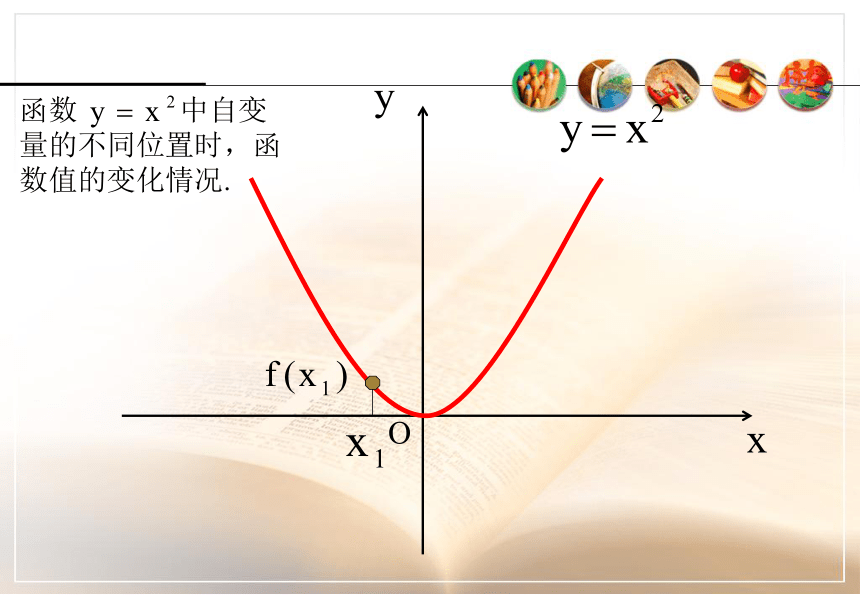
文档简介
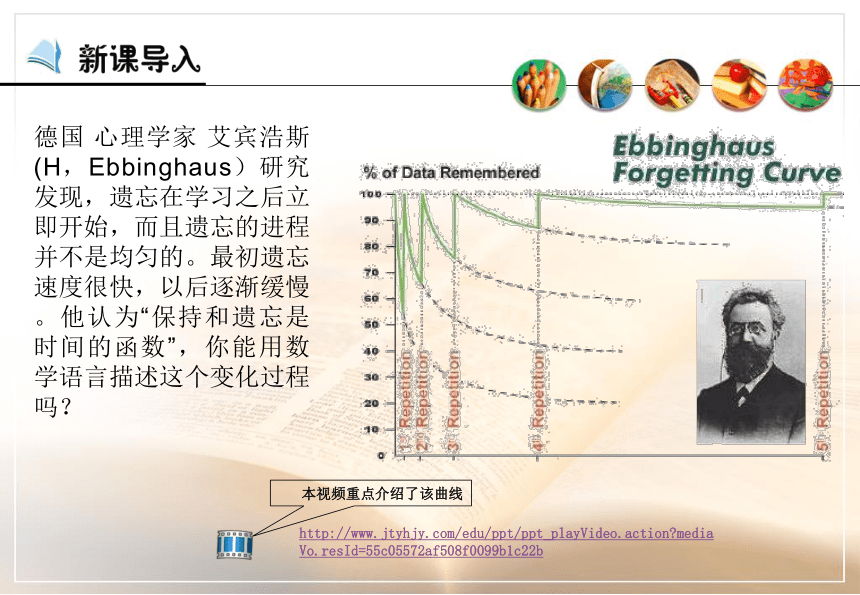
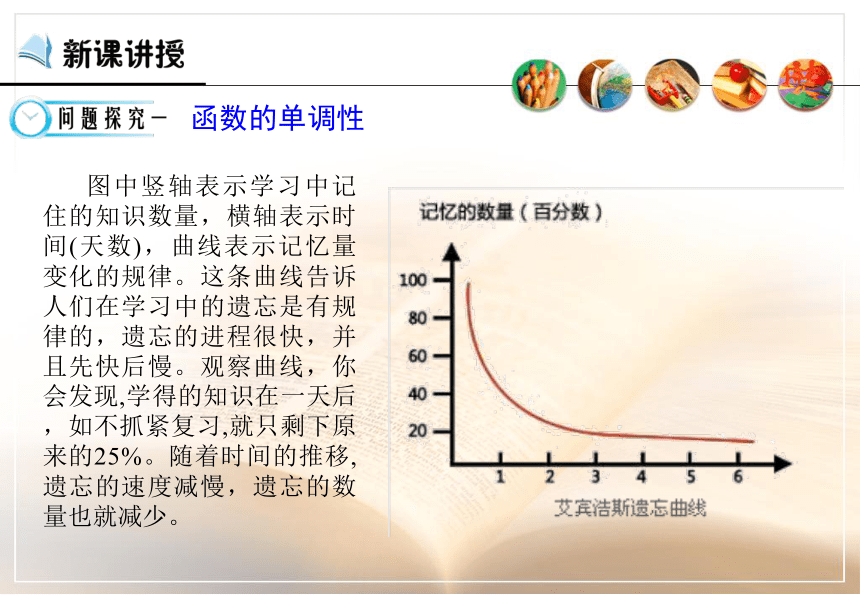
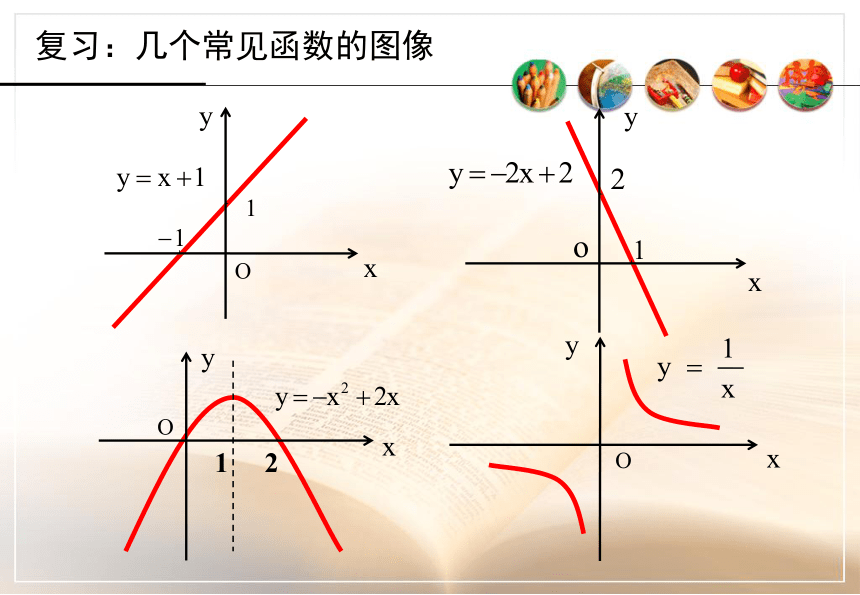
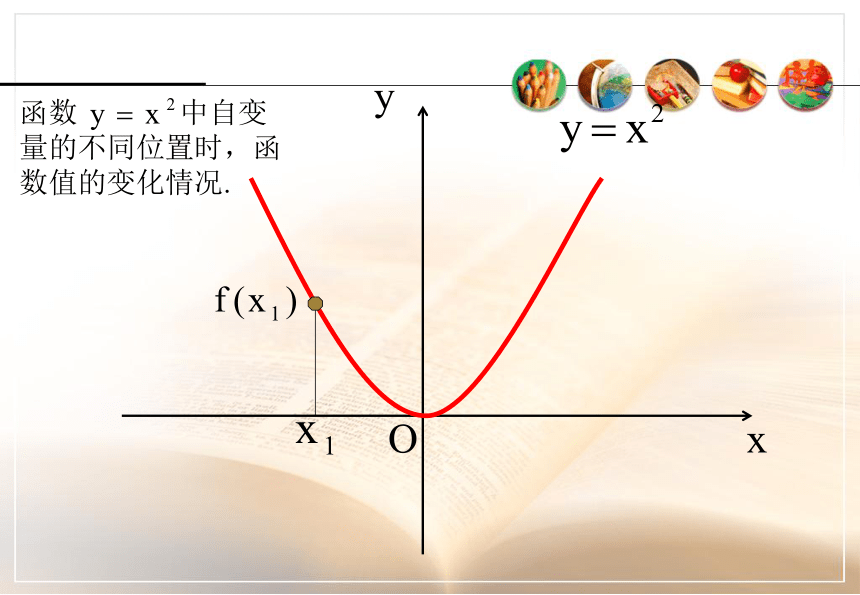
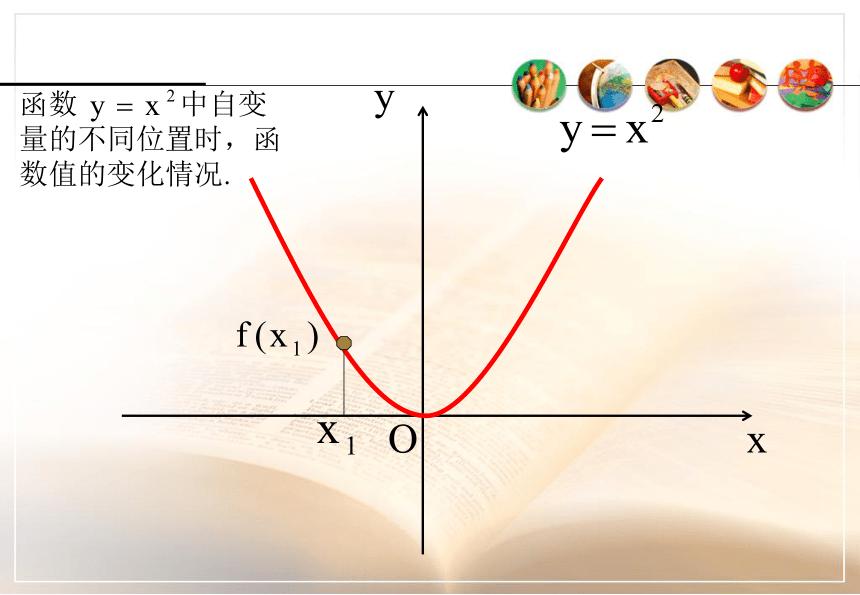
课件27张PPT。函数的基本性质---单调性复习函数的表示方法2常见的函数图象:正比例函数、反比例函数、一次函数、二次函数3课前复习德国 心理学家 艾宾浩斯(H,Ebbinghaus)研究发现,遗忘在学习之后立即开始,而且遗忘的进程并不是均匀的。最初遗忘速度很快,以后逐渐缓慢。他认为“保持和遗忘是时间的函数”,你能用数学语言描述这个变化过程吗? 本视频重点介绍了该曲线http://www.jtyhjy.com/edu/ppt/ppt_playVideo.action?mediaVo.resId=55c05572af508f0099b1c22b 图中竖轴表示学习中记住的知识数量,横轴表示时间(天数),曲线表示记忆量变化的规律。这条曲线告诉人们在学习中的遗忘是有规律的,遗忘的进程很快,并且先快后慢。观察曲线,你会发现,学得的知识在一天后,如不抓紧复习,就只剩下原来的25%。随着时间的推移,遗忘的速度减慢,遗忘的数量也就减少。 函数的单调性o复习:几个常见函数的图像Oxy函数 中自变量的不同位置时,函数值的变化情况.Oxy函数 中自变量的不同位置时,函数值的变化情况.Oxy函数 中自变量的不同位置时,函数值的变化情况.Oxy函数 中自变量的不同位置时,函数值的变化情况.Oxy函数 中自变量的不同位置时,函数值的变化情况.Oxy函数 中自变量的不同位置时,函数值的变化情况.Oxy函数 中自变量的不同位置时,函数值的变化情况.Oxy函数 中自变量的不同位置时,函数值的变化情况.Oxy函数 中自变量的不同位置时,函数值的变化情况.能用图象上动点P(x,y)的横、纵坐标关系来说明上升或下降趋势吗?先下降后上升下降上升一般地,设函数f(x)的定义域为I: 如果对于定义域I内某个区间D上的任意两个自变量的
值 ,当 时,都有 ,那么就说函数
在区间D上是增函数.如果对于定义域I内某个区间D上的任意两个自变量的值 ,当 时,都有 ,那么就说函数
在区间D上是减函数.如果函数 在区间D上是增函数或减函数,那么就说函数 在这一区间具有(严格的)单调性,区间D叫做 的单调区间.例1、(1) 下图是定义在[-5,5]上的函数y=f(x)的图象,根据图象说出y=f(x)的单调区间,以及在每一单调区间上, y=f(x)是增函数还是减函数.解:单调递增区间:[-2,1],[3,5]单调递减区间:[-5,-2),(-3,3)例题展示-5 -4 -3 -2 -1 O 1 2 3 4 5 XY?例2 证明函数f(x)=3x+2在R上是增函数.证明:例3.物理学中的玻意耳定律 (k为正常数)告诉我们,对于
一定量的气体,当其体积减小时,压强 p将增大,试用函数的单调性证明之。
取值定号结论练习1:证明函数 在区间 是增函数。2:证明函数 在(1,+∞)上为增函数. 用定义证明函数单调性的步骤:
1.取值
2.作差变形
3.定号
4.判断 (1)当 时,
则 在区间上是增函数
(2)当 时,
则 在区间上是减函数
规律总结确定还是2、函数单调性的定义;3、证明函数单调性的步骤;1、单调函数的图象特征;思考:讨论函数
在(-2,2)内的单调性.2、 证明函数f(x)=x 在(-∞,+∞)上是增函数.3
值 ,当 时,都有 ,那么就说函数
在区间D上是增函数.如果对于定义域I内某个区间D上的任意两个自变量的值 ,当 时,都有 ,那么就说函数
在区间D上是减函数.如果函数 在区间D上是增函数或减函数,那么就说函数 在这一区间具有(严格的)单调性,区间D叫做 的单调区间.例1、(1) 下图是定义在[-5,5]上的函数y=f(x)的图象,根据图象说出y=f(x)的单调区间,以及在每一单调区间上, y=f(x)是增函数还是减函数.解:单调递增区间:[-2,1],[3,5]单调递减区间:[-5,-2),(-3,3)例题展示-5 -4 -3 -2 -1 O 1 2 3 4 5 XY?例2 证明函数f(x)=3x+2在R上是增函数.证明:例3.物理学中的玻意耳定律 (k为正常数)告诉我们,对于
一定量的气体,当其体积减小时,压强 p将增大,试用函数的单调性证明之。
取值定号结论练习1:证明函数 在区间 是增函数。2:证明函数 在(1,+∞)上为增函数. 用定义证明函数单调性的步骤:
1.取值
2.作差变形
3.定号
4.判断 (1)当 时,
则 在区间上是增函数
(2)当 时,
则 在区间上是减函数
规律总结确定还是2、函数单调性的定义;3、证明函数单调性的步骤;1、单调函数的图象特征;思考:讨论函数
在(-2,2)内的单调性.2、 证明函数f(x)=x 在(-∞,+∞)上是增函数.3
