5.3概率 同步练习(含解析)2023——2024学年人教B版(2019)高中数学必修第二册
文档属性
| 名称 | 5.3概率 同步练习(含解析)2023——2024学年人教B版(2019)高中数学必修第二册 |

|
|
| 格式 | docx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-21 21:28:41 | ||
图片预览




文档简介
5.3概率同步练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.从甲袋中摸出一个红球的概率是,从乙袋中摸出一个红球的概率是,现从两袋各摸出一个球,记事件A:2个球都是红球,事件B:2个球中恰有1个红球,事件C:2个球至少有1个红球,事件D:2个球不都是红球,则下列说法正确的是( )
A.事件A与事件互斥 B.
C.事件A与事件D对立 D.
2.在素数研究中,华裔数学家张益唐证明了孪生素数猜想的一个弱化形式,孪生素数是指相差为2的素数对,例如3和5,11和13等.从不超过10的正奇数中随机抽取2个,则这2个奇数是孪生素数的概率为( )
A. B. C. D.
3.在一次考试中有一道4个选项的双选题,其中B和C是正确选项,A和D是错误选项,甲、乙两名同学都完全不会这道题目,只能在4个选项中随机选取两个选项.设事件“甲、乙两人所选选项恰有一个相同”,事件“甲、乙两人所选选项完全不同”,事件“甲、乙两人所选选项完全相同”,事件“甲、乙两人均未选择B选项”,则( )
A.事件M与事件N相互独立 B.事件X与事件Y相互独立
C.事件M与事件Y相互独立 D.事件N与事件Y相互独立
4.端午节是我国传统节日,随着淄博烧烤的示范作用,徐州烧烤也备受游客欢迎,经过随机发放并回收调查问卷,在连云港、宿迁、淮安三个淮海经济圈城市中对广大市民的端午短途游进行了解,每个城市回收300份调查问卷,其中连云港市有100份勾选去徐州旅游,宿迁市有120份勾选去徐州旅游,淮安市有75份勾选去徐州旅游.端午节期间,连云港游客甲,宿迁游客乙,淮安游客丙打算外出旅游,假定3人的行动相互之间没有影响,那么这段时间内三个人中至少有1人来徐州旅游的概率约为( )
A. B. C. D.
5.有一批货物需要用汽车从生产商所在城市甲运至销售商所在城市乙,已知从城市甲到城市乙只有两条公路,据调查统计,通过这两条公路从城市甲到城市乙的200辆汽车所用时间的频数分布情况如下表所示
所用时间天数 10 11 12 13
通过公路1的频数 20 40 20 20
通过公路2的频数 10 40 40 10
假设汽车A只能在约定日期某月某日的前11天出发,汽车B只能在约定日期的前12天出发将频率视为概率,为了在各自允许的时间内将货物运至城市乙,汽车A和汽车B选择的最佳路径分别为( )
A.公路1和公路2 B.公路2和公路1 C.公路2和公路2 D.公路1和公路1
6.某单位有职工450人,其中男职工150人,现为了解职工健康情况,该单位采取分层随机抽样的方法抽取了一个容量为90的样本,得出体重情况:男性平均体重为63千克;女性平均体重为54千克.则下列说法不正确的是( )
A.抽查的样本中女职工人数为60
B.该单位男职工的体重普遍比女职工较重
C.估计该单位职工平均体重为58.5
D.每一位男或女职工被抽中的可能性均为
7.一次课外活动中,某班60名同学均参加了羽毛球或乒乓球运动,其中37人参加了羽毛球运动,38人参加了乒乓球运动.若从该班随机抽取一名同学,则该同学既参加了羽毛球运动又参加了乒乓球运动的概率为( ).
A. B. C. D.
8.信宜市是广东省首个“中国慈孝文化之乡”.为弘扬传统慈孝文化,信宜某小学开展为父母捶背活动,要求同学们在某周的周一至周五任选两天为父母捶背,则该校的同学甲连续两天为父母捶背的概率为( )
A. B. C. D.
二、多选题
9.有个相同的球,分别标有数字,,,,,,从中有放回的随机取两次,每次取个球,甲表示事件“第一次取出的球的数字是”,乙表示事件“第二次取出的球的数字是”,丙表示事件“两次取出的球的数字之和是”,丁表示事件“两次取出的球的数字之和是”,则( )
A.(丙) B.(丁) C.乙与丙相互独立 D.甲与丁相互独立
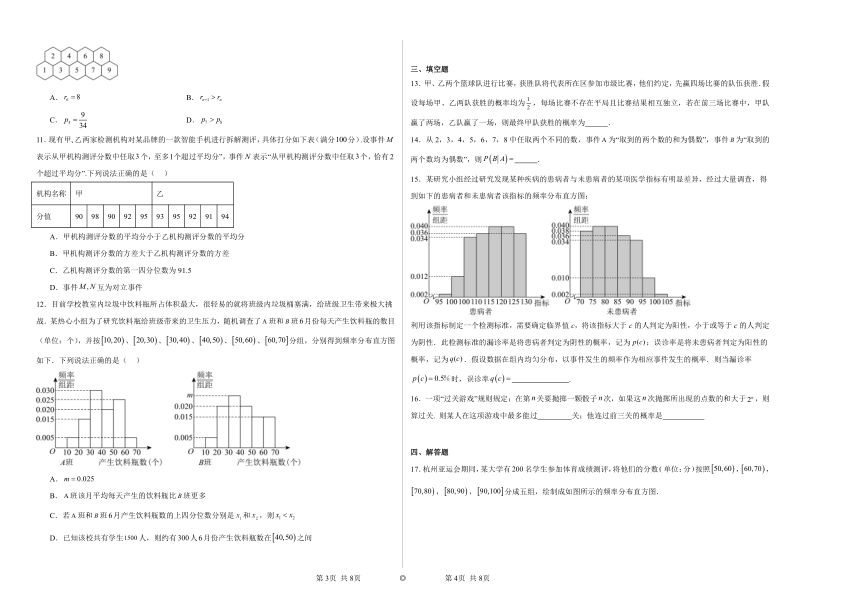
10.如图,从1开始出发,一次移动是指:从某一格开始只能移动到邻近的一格,并且总是向右或右上或右下移动,而一条移动路线由若干次移动构成,如从1移动到9,就是一条移动路线.从1移动到数字的不同路线条数记为,从1移动到9的事件中,跳过数字的概率记为,则下列结论正确的是( )
A. B.
C. D.
11.现有甲 乙两家检测机构对某品牌的一款智能手机进行拆解测评,具体打分如下表(满分分).设事件表示从甲机构测评分数中任取个,至多个超过平均分”,事件表示“从甲机构测评分数中任取个,恰有个超过平均分”.下列说法正确的是( )
机构名称 甲 乙
分值 90 98 90 92 95 93 95 92 91 94
A.甲机构测评分数的平均分小于乙机构测评分数的平均分
B.甲机构测评分数的方差大于乙机构测评分数的方差
C.乙机构测评分数的第一四分位数为91.5
D.事件互为对立事件
12.目前学校教室内垃圾中饮料瓶所占体积最大,很轻易的就将班级内垃圾桶塞满,给班级卫生带来极大挑战.某热心小组为了研究饮料瓶给班级带来的卫生压力,随机调查了班和班月份每天产生饮料瓶的数目(单位:个),并按、、、、、分组,分别得到频率分布直方图如下.下列说法正确的是( )
A.
B.班该月平均每天产生的饮料瓶比班更多
C.若班和班月产生饮料瓶数的上四分位数分别是和,则
D.已知该校共有学生人,则约有人月份产生饮料瓶数在之间
三、填空题
13.甲、乙两个篮球队进行比赛,获胜队将代表所在区参加市级比赛,他们约定,先赢四场比赛的队伍获胜.假设每场甲、乙两队获胜的概率均为,每场比赛不存在平局且比赛结果相互独立,若在前三场比赛中,甲队赢了两场,乙队赢了一场,则最终甲队获胜的概率为 .
14.从2,3,4,5,6,7,8中任取两个不同的数,事件为“取到的两个数的和为偶数”,事件为“取到的两个数均为偶数”,则 .
15.某研究小组经过研究发现某种疾病的患病者与未患病者的某项医学指标有明显差异,经过大量调查,得到如下的患病者和未患病者该指标的频率分布直方图:
利用该指标制定一个检测标准,需要确定临界值c,将该指标大于c的人判定为阳性,小于或等于c的人判定为阴性.此检测标准的漏诊率是将患病者判定为阴性的概率,记为;误诊率是将未患病者判定为阳性的概率,记为.假设数据在组内均匀分布,以事件发生的频率作为相应事件发生的概率.则当漏诊率时,误诊率 .
16.一项“过关游戏”规则规定:在第关要抛掷一颗骰子次,如果这次抛掷所出现的点数的和大于,则算过关. 则某人在这项游戏中最多能过 关;他连过前三关的概率是
四、解答题
17.杭州亚运会期同,某大学有名学生参加体育成绩测评,将他们的分数单位:分按照,,,,分成五组,绘制成如图所示的频率分布直方图.
(1)求的值及这组数据的第百分位数;
(2)按分层陆机抽样的方法从分数在和内的学生中抽取人,再从这人中任选人,求这人成绩之差的绝对值大于分的概率.
18.为了营造浓厚的读书氛围,激发学生的阅读兴趣,净化学生的精神世界,赤峰市教育局组织了书香校园知识大赛,全市共有名学生参加知识大赛初赛,所有学生的成绩均在区间内,组委会将初赛成绩分成组:加以统计,得到如图所示的频率分布直方图.
(1)试估计这名学生初赛成绩的平均数及中位数(同一组的数据以该组区间的中间值作为代表);(中位数精确到0.01)
(2)组委会在成绩为的学生中用分层抽样的方法随机抽取人,然后再从抽取的人中任选取人进行调查,求选取的人中恰有人成绩在内的概率.
19.某学校为了解本校历史 物理方向学生的学业水平模拟测试数学成绩情况,分别从物理方向的学生中随机抽取60人的成绩得到样本甲,从历史方向的学生中随机抽取人的成绩得到样本乙,根据两个样本数据分别得到如下直方图:
已知乙样本中数据在的有10个.
(1)求和乙样本直方图中的值;
(2)试估计该校物理方向的学生本次模拟测试数学成绩的平均值和历史方向的学生本次模拟测试数学成绩的中位数(同一组中的数据用该组区间中点值为代表).
(3)采用分层抽样的方法从甲样本数据中分数在和的学生中抽取6人,并从这6人中任取2人,求这两人分数都在中的概率.
20.2023年为普及航天知识,某校开展了“航天知识竞赛”活动,现从参加该竞赛的学生中随机抽取了80名,统计他们的成绩(满分100分),其中成绩不低于80分的学生被评为“航天达人”,将数据整理后绘制成如图所示的频率分布直方图.
(1)若该中学参加这次竞赛的共有3000名学生,试估计全校这次竞赛中“航天达人”的人数;
(2)估计参加这次竞赛的学生成绩的第75百分位数;
(3)若在抽取的80名学生中,利用分层随机抽样的方法从成绩不低于70分的学生中随机抽取6人,再从6人中选择2人作为学生代表,求被选中的2人均为航天达人的概率.
21.某中学高三年级某班50名学生期中考试数学成绩的频率分布直方图如图所示,成绩分组区间为:,,,,,,.其中,且.物理成绩统计如表.(说明:数学满分150分,物理满分100分)
物理成绩统计表
分组
频数 6 9 20 10 5
(1)根据频率分布直方图,请估计数学成绩的平均分(同一组数据用该区间的中点值代表);
(2)若数学成绩不低于140分的为“优”,物理成绩不低于90分的为“优”,已知本班中至少有一个“优”的同学总数为6人,从数学成绩为“优”的同学中随机抽取2人,求两人恰好均为物理成绩为“优”的概率.
第1页 共4页 ◎ 第2页 共4页
第1页 共4页 ◎ 第2页 共4页
参考答案:
1.C
【分析】记从甲袋中摸出一个红球的事件为,从乙袋中摸出一个红球的事件为,根据互斥和对立事件的定义分析判断AC;根据独立事件概率乘法公式以及互斥事件概率求法分析判断BD.
【详解】记从甲袋中摸出一个红球的事件为,从乙袋中摸出一个红球的事件为,
可知,相互独立,
于是:,
由此可得:可能同时发生,A错误;互为对立事件,C正确;
因为,所以,B错误;
因为,所以,D错误.
故选:C.
2.C
【分析】利用古典概型计算公式先列举出所有基本事件数,再求出是孪生素数的事件数即可求得结果.
【详解】不超过10的正奇数有,共5个,从中随机抽取2个,
共有,10种情况,
其中孪生素数有,共2种情况,
由古典概型可得这2个奇数是孪生素数的概率为.
故选:C.
3.C
【分析】根据互斥、相互独立事件的乘法公式对选项一一判断即可得出答案.
【详解】依题意甲、乙两人所选选项有如下情形:
①有一个选项相同,②两个选项相同,③两个选项不相同,
所以,,,,
因为事件与事件互斥,所以,又,
所以事件M与事件N不相互独立,故A错误;
,故B错误;
由,则事件M与事件Y相互独立,故C正确;
因为事件N与事件Y互斥,所以,又,
所以事件N与事件Y不相互独立,故D错误.
故选:C.
【点睛】关键点点睛:本题的关键点在于先求出,,,,再根据互斥、相互独立事件的乘法公式对选项一一判断即可.
4.B
【分析】借助频率估计概率后,结合相互独立事件的概率公式计算即可得.
【详解】甲来徐州旅游的概率约为,乙来徐州旅游的概率约为,
丙来徐州旅游的概率约为,
则三人都没有来徐州旅游的概率约为,
故三个人中至少有1人来徐州旅游的概率约为.
故选:B.
5.A
【分析】将频率视为概率,分别计算汽车,选择公路1和公路2按时到达的概率,以此判断最佳路径.
【详解】频率分布表如下:
所用时间天数 10 11 12 13
通过公路1的频率
通过公路2的频率
设,分别表示事件“汽车A选择公路1时在约定时间内将货物运至城市乙”和“汽车A选择公路2时在约定时间内将货物运至城市乙”,
,分别表示事件“汽车B选择公路1时在约定时间内将货物运至城市乙”和“汽车B选择公路2时在定时间内将货物运至城市乙”,
以频率估计概率得,,,,
所以汽车A和汽车B选择的最佳路径分别为公路1和公路2.
故选:.
6.C
【分析】根据分层抽样、平均数、古典概率等知识确定正确答案.
【详解】A选项,抽查的样本中女职工人数为,A选项正确.
B选项,男性平均体重为63千克;女性平均体重为54千克,
所以该单位男职工的体重普遍比女职工较重,B选项正确.
C选项,估计该单位职工平均体重为,C选项错误.
D选项,每一位男或女职工被抽中的可能性均为,D选项正确.
故选:C
7.A
【分析】计算出该班学生中既参加了羽毛球运动又参加了乒乓球运动的人数,利用古典概型概率计算公式计算即可.
【详解】依题意,该班学生中既参加了羽毛球运动又参加了乒乓球运动有:
(名),
故从该班随机抽取一名同学,
该同学既参加了羽毛球运动又参加了乒乓球运动的概率为,
故选:A.
8.C
【分析】根据给定条件,求出周一至周五任选两天的试验的样本空间,再求出连续两天的事件含有的样本点,进而求出古典概率.
【详解】令周一至周五的5天依次为1,2,3,4,5,
则周一至周五任选两天的样本空间,共10个样本点,
连续两天的事件,共4个样本点,
所以该校的同学甲连续两天为父母捶背的概率为.
故选:C
9.AD
【分析】
利用古典概型的概率计算各事件概率,再根据独立事件概率的关系依次判断即可.
【详解】依题意基本事件总数为个,
“第一次取出的球的数字是”的基本事件有个,
“第二次取出的球的数字是”的基本事件有个,
“两次取出的球的数字之和为”的基本事件有共个,
“两次取出的球的数字之和为”的基本事件有共个,
所以(丙),(丁);(甲)(乙),故A正确,B错误;
又同时满足事件甲、丁的基本事件有共个,同时满足事件乙、丙的基本事件有共个,
所以(乙丙)(乙)(丙),所以乙与丙不相互独立,故C错误;
所以(甲丁)(甲)(丁),所以甲与丁相互独立,故D正确;
故选:AD.
10.ABC
【分析】画出树状图,结合图形及古典概型逐项分析判断.
【详解】画出树状图,结合图形
结合树状图可知:,
对于选项A:可知,故A正确;
对于选项B: 均有,故B正确;
对于选项C:因为,不经过数字5的路线有9条,所以,故C正确;
对于选项D:因为,所以,故D错误;
故选:ABC.
11.BD
【分析】直接由平均数、方差、百分位数及对立事件的概念,逐一对各个选项分析判断,即可得出结果.
【详解】对于选项A,甲机构测评分数的平均分,
乙机构测评分数的平均分,所以选项A错误,
对于选项B,甲机构测评分数的方差,
,所以选项B正确,
对于选项C,乙机构测评分数从小排到大为:91,92,93,94,95,
又,所以乙机构测评分数的第一四分位数为92,所以选项C错误,
对于选项D,因为甲机构测评分数中有且仅有2个测评分数超过平均分,由对立事件的定义知,事件互为对立事件,所以选项D正确,
故选:BD.
12.ACD
【分析】A选项,根据频率之和为列出方程,求出;B选项,用中间值作代表,求出班和B班该月平均每天产生的饮料瓶个数估计值,比较出结果;C选项,利用百分位数的定义求出,,故C正确;D选项,结合频率分布直方图得到该校学生月份产生饮料瓶数在的频率为0.2,从而求出D正确.
【详解】对于A选项,由,解得,A正确;
对于B选项,班该月平均每天产生的饮料瓶个数估计为,
班该月平均每天产生的饮料瓶个数估计为,
因为,所以班该月平均每天产生的饮料瓶比班更少,B错误;
对于C选项,,,
故班月产生饮料瓶数的上四分位数位于内,
故,解得,
,
,
故班月产生饮料瓶数的上四分位数位于内,
故,解得,故,C正确;
对于D选项,班和班月产生饮料瓶数在的频率均为,
故该校学生月份产生饮料瓶数在的频率也为,
,所以该校约有人月份产生饮料瓶数在之间,D正确.
故选:ACD
13./
【分析】
考虑先赢四场比赛的队伍获胜,甲队已经赢了两场,故只需再先赢两场则获胜,分析得到甲在随后进行的场次可以有两场连胜,也可输一场赢两场(含两种情况),还可以输两场赢两场(含三种情况),分别计算概率,再利用互斥事件的概率加法公式即得.
【详解】
由题意得甲、乙两队获胜的概率均为,且最多再进行四场比赛,最少再进行两场比赛.
则①再进行两场比赛甲队获胜的概率为;
②再进行三场比赛甲队获胜的概率为;
③再进行四场比赛甲队获胜的概率为,
由互斥事件的概率加法公式,可得最终甲队获胜的概率为.
故答案为.
14.
【分析】
利用条件概率的计算公式可求
【详解】表示“取到的两个数为偶数且和为偶数”,,
而,故,
故答案为:.
15.
【分析】先根据左边的频率分布直方图得到,再根据右边的频率分布直方图可得.
【详解】依题可知,左边图形第一个小矩形的面积为,所以,
所以,解得:,
由右边的频率分布直方图可得.
故答案为:
16.
【分析】每关得到的最大点数为,令,利用作差法可求得数列单调性,由此可确定当时,,从而得到结论;分别计算该人通过第一、第二和第三关的概率,根据独立事件概率乘法公式可求得结果.
【详解】若每次抛掷一颗骰子都能得到最大点数点,则第关抛掷的点数和为,
令,则,
则当时,数列单调递增;当时,数列单调递减;
又,,,
当时,,则某人在这项游戏中最多能过关;
该人第一关所有可能的结果为,则通过第一关的概率;
该人第二关所有可能的结果有种,则不能过关的基本事件个数为的正整数解的个数,则有种,
通过第二关的概率;
该人第三关所有可能的结果有种,则不能过关的基本事件个数为的正整数解得个数,则有种,
通过第三关的概率;
连过前三关的概率.
故答案为:;.
17.(1),
(2)
【分析】
(1)利用频率分布直方图中各个小矩形的面积之和为可求出的值,再利用百分位数的定义求这组数据的第百分位数即可;
(2)利用古典概型的概率公式求解.
【详解】(1)
由频率分布直方图可知,,
解得,
因为,,
所以这组数据的第百分位数位于,设其为,
则,
解得,即这组数据的第百分位数为;
(2)
由题可知,从分数在内的学生中抽取人,记为,,
则分数在内的学生中抽取人,记为,,,,
从中任选人,则所有可能结果有:,,,,,,,,
,,,,,,共个,
满足这人成绩之差的绝对值大于分的有,,,,,,,共个,
故所求的概率.
18.(1)平均数76,中位数约为76.67.
(2).
【分析】
(1)利用频率分布直方图,根据平均数和中位数的计算方法即可求得答案;
(2)确定成绩为的学生中成绩在和内的人数比例,即可确定抽查的5人中各组抽的人数,列举出抽取的人中任选取人的所有可能情况,再列出选取的人中恰有人成绩在内的情况,根据古典概型的概率公式即可求得答案.
【详解】(1)
,
设中位数为,因为前组的频率之和为,
而前2组的频率之和为,所以,
由,
解得:,
故可估计这500名学生初赛成绩的中位数约为;
(2)
根据分层抽样,由频率分布直方图知成绩在和内的人数比例为,
所以抽取的5人中,成绩在内的有人,记为,;
成绩在内的有人,记为,,,
从5人中任意选取2人,有,,,,,,,,,,共10种可能;
其中选取的2人中恰有1人成绩在区间内的有,,,,,,共6种可能;
故所求的概率为.
19.(1);;
(2)平均值81.5,中位数82;
(3)
【分析】
(1)根据频率定义即可求出,再根据小矩形面积和为1即可求出值;
(2)根据平均数和中位数定义计算即可;
(3)列出所有情况和满足题意的情况,再利用古典概率公式即可.
【详解】(1)由直方图可知,乙样本中数据在的频率为,
则,解得;
由乙样本数据直方图可知,,
解得;
(2)甲样本数据的平均值估计值为
,
乙样本数据直方图中前3组的频率之和为,
前4组的频率之和为,
所以乙样本数据的中位数在第4组,设中位数为,
,
解得,所以乙样本数据的中位数为82.
(3)由频率分布直方图可知从分数在和的学生中分别抽取2人和4人,
将从分数在中抽取的2名学生分别记为,从分数在中抽取的4名学生分别记为,
则从这6人中随机抽取2人的基本事件有
,共15个,
所抽取的两人分数都在中的基本事件有6个,所以所求概率为.
20.(1)
(2)
(3)
【分析】(1)由频率分布直方图求出成绩在内的频率,即可估计人数;
(2)根据百分位数计算规则计算可得;
(3)先按照分层抽样求出各层人数,再利用列举法结合古典概型即可得解.
【详解】(1)由频率分布直方图可知,
成绩在内的频率为,
则估计全校这次竞赛中“航天达人”的人数约为人;
(2)由频率分布直方图可知,成绩在内的频率为,
成绩在内的频率为,
成绩在内的频率为,
成绩在内的频率为,
成绩在内的频率为,
所以成绩在分以下的学生所占的比例为,
成绩在分以下的学生所占的比例为,
所以成绩的分位数一定在内,即,
因此估计参加这次竞赛的学生成绩的分位数为;
(3)因为,,,
所以从成绩在,,内的学生中分别抽取了人,人,人,
其中有人为航天达人,设为,
有人不是航天达人,设为,
则从6人中选择2人作为学生代表,
有,
共种,
其中2人均为航天达人为共种,
所以被选中的2人均为航天达人的概率为.
21.(1)117.8分;
(2).
【分析】(1)计算,再利用频率分布直方图估计平均数.
(2)计算得到两科均为“优”的人数为3人,设两科均为“优”的同学为,物理成绩不是“优”的同学为B,列出所有情况,统计满足条件的情况,得到概率.
【详解】(1)依题意,,
解得,
所以数学成绩的平均分:
.
(2)数学成绩为“优”的同学有人,物理成绩为“优”有5人,
因为至少有一个“优”的同学总数为6名同学,则两科均为“优”的人数为3人.
设两科均为“优”的同学为,物理成绩不是“优”的同学为B,
则从4人中随机抽取2人的所有情况有:,
符合题意的情况有:,
故两人恰好均为物理成绩“优”的概率.
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.从甲袋中摸出一个红球的概率是,从乙袋中摸出一个红球的概率是,现从两袋各摸出一个球,记事件A:2个球都是红球,事件B:2个球中恰有1个红球,事件C:2个球至少有1个红球,事件D:2个球不都是红球,则下列说法正确的是( )
A.事件A与事件互斥 B.
C.事件A与事件D对立 D.
2.在素数研究中,华裔数学家张益唐证明了孪生素数猜想的一个弱化形式,孪生素数是指相差为2的素数对,例如3和5,11和13等.从不超过10的正奇数中随机抽取2个,则这2个奇数是孪生素数的概率为( )
A. B. C. D.
3.在一次考试中有一道4个选项的双选题,其中B和C是正确选项,A和D是错误选项,甲、乙两名同学都完全不会这道题目,只能在4个选项中随机选取两个选项.设事件“甲、乙两人所选选项恰有一个相同”,事件“甲、乙两人所选选项完全不同”,事件“甲、乙两人所选选项完全相同”,事件“甲、乙两人均未选择B选项”,则( )
A.事件M与事件N相互独立 B.事件X与事件Y相互独立
C.事件M与事件Y相互独立 D.事件N与事件Y相互独立
4.端午节是我国传统节日,随着淄博烧烤的示范作用,徐州烧烤也备受游客欢迎,经过随机发放并回收调查问卷,在连云港、宿迁、淮安三个淮海经济圈城市中对广大市民的端午短途游进行了解,每个城市回收300份调查问卷,其中连云港市有100份勾选去徐州旅游,宿迁市有120份勾选去徐州旅游,淮安市有75份勾选去徐州旅游.端午节期间,连云港游客甲,宿迁游客乙,淮安游客丙打算外出旅游,假定3人的行动相互之间没有影响,那么这段时间内三个人中至少有1人来徐州旅游的概率约为( )
A. B. C. D.
5.有一批货物需要用汽车从生产商所在城市甲运至销售商所在城市乙,已知从城市甲到城市乙只有两条公路,据调查统计,通过这两条公路从城市甲到城市乙的200辆汽车所用时间的频数分布情况如下表所示
所用时间天数 10 11 12 13
通过公路1的频数 20 40 20 20
通过公路2的频数 10 40 40 10
假设汽车A只能在约定日期某月某日的前11天出发,汽车B只能在约定日期的前12天出发将频率视为概率,为了在各自允许的时间内将货物运至城市乙,汽车A和汽车B选择的最佳路径分别为( )
A.公路1和公路2 B.公路2和公路1 C.公路2和公路2 D.公路1和公路1
6.某单位有职工450人,其中男职工150人,现为了解职工健康情况,该单位采取分层随机抽样的方法抽取了一个容量为90的样本,得出体重情况:男性平均体重为63千克;女性平均体重为54千克.则下列说法不正确的是( )
A.抽查的样本中女职工人数为60
B.该单位男职工的体重普遍比女职工较重
C.估计该单位职工平均体重为58.5
D.每一位男或女职工被抽中的可能性均为
7.一次课外活动中,某班60名同学均参加了羽毛球或乒乓球运动,其中37人参加了羽毛球运动,38人参加了乒乓球运动.若从该班随机抽取一名同学,则该同学既参加了羽毛球运动又参加了乒乓球运动的概率为( ).
A. B. C. D.
8.信宜市是广东省首个“中国慈孝文化之乡”.为弘扬传统慈孝文化,信宜某小学开展为父母捶背活动,要求同学们在某周的周一至周五任选两天为父母捶背,则该校的同学甲连续两天为父母捶背的概率为( )
A. B. C. D.
二、多选题
9.有个相同的球,分别标有数字,,,,,,从中有放回的随机取两次,每次取个球,甲表示事件“第一次取出的球的数字是”,乙表示事件“第二次取出的球的数字是”,丙表示事件“两次取出的球的数字之和是”,丁表示事件“两次取出的球的数字之和是”,则( )
A.(丙) B.(丁) C.乙与丙相互独立 D.甲与丁相互独立
10.如图,从1开始出发,一次移动是指:从某一格开始只能移动到邻近的一格,并且总是向右或右上或右下移动,而一条移动路线由若干次移动构成,如从1移动到9,就是一条移动路线.从1移动到数字的不同路线条数记为,从1移动到9的事件中,跳过数字的概率记为,则下列结论正确的是( )
A. B.
C. D.
11.现有甲 乙两家检测机构对某品牌的一款智能手机进行拆解测评,具体打分如下表(满分分).设事件表示从甲机构测评分数中任取个,至多个超过平均分”,事件表示“从甲机构测评分数中任取个,恰有个超过平均分”.下列说法正确的是( )
机构名称 甲 乙
分值 90 98 90 92 95 93 95 92 91 94
A.甲机构测评分数的平均分小于乙机构测评分数的平均分
B.甲机构测评分数的方差大于乙机构测评分数的方差
C.乙机构测评分数的第一四分位数为91.5
D.事件互为对立事件
12.目前学校教室内垃圾中饮料瓶所占体积最大,很轻易的就将班级内垃圾桶塞满,给班级卫生带来极大挑战.某热心小组为了研究饮料瓶给班级带来的卫生压力,随机调查了班和班月份每天产生饮料瓶的数目(单位:个),并按、、、、、分组,分别得到频率分布直方图如下.下列说法正确的是( )
A.
B.班该月平均每天产生的饮料瓶比班更多
C.若班和班月产生饮料瓶数的上四分位数分别是和,则
D.已知该校共有学生人,则约有人月份产生饮料瓶数在之间
三、填空题
13.甲、乙两个篮球队进行比赛,获胜队将代表所在区参加市级比赛,他们约定,先赢四场比赛的队伍获胜.假设每场甲、乙两队获胜的概率均为,每场比赛不存在平局且比赛结果相互独立,若在前三场比赛中,甲队赢了两场,乙队赢了一场,则最终甲队获胜的概率为 .
14.从2,3,4,5,6,7,8中任取两个不同的数,事件为“取到的两个数的和为偶数”,事件为“取到的两个数均为偶数”,则 .
15.某研究小组经过研究发现某种疾病的患病者与未患病者的某项医学指标有明显差异,经过大量调查,得到如下的患病者和未患病者该指标的频率分布直方图:
利用该指标制定一个检测标准,需要确定临界值c,将该指标大于c的人判定为阳性,小于或等于c的人判定为阴性.此检测标准的漏诊率是将患病者判定为阴性的概率,记为;误诊率是将未患病者判定为阳性的概率,记为.假设数据在组内均匀分布,以事件发生的频率作为相应事件发生的概率.则当漏诊率时,误诊率 .
16.一项“过关游戏”规则规定:在第关要抛掷一颗骰子次,如果这次抛掷所出现的点数的和大于,则算过关. 则某人在这项游戏中最多能过 关;他连过前三关的概率是
四、解答题
17.杭州亚运会期同,某大学有名学生参加体育成绩测评,将他们的分数单位:分按照,,,,分成五组,绘制成如图所示的频率分布直方图.
(1)求的值及这组数据的第百分位数;
(2)按分层陆机抽样的方法从分数在和内的学生中抽取人,再从这人中任选人,求这人成绩之差的绝对值大于分的概率.
18.为了营造浓厚的读书氛围,激发学生的阅读兴趣,净化学生的精神世界,赤峰市教育局组织了书香校园知识大赛,全市共有名学生参加知识大赛初赛,所有学生的成绩均在区间内,组委会将初赛成绩分成组:加以统计,得到如图所示的频率分布直方图.
(1)试估计这名学生初赛成绩的平均数及中位数(同一组的数据以该组区间的中间值作为代表);(中位数精确到0.01)
(2)组委会在成绩为的学生中用分层抽样的方法随机抽取人,然后再从抽取的人中任选取人进行调查,求选取的人中恰有人成绩在内的概率.
19.某学校为了解本校历史 物理方向学生的学业水平模拟测试数学成绩情况,分别从物理方向的学生中随机抽取60人的成绩得到样本甲,从历史方向的学生中随机抽取人的成绩得到样本乙,根据两个样本数据分别得到如下直方图:
已知乙样本中数据在的有10个.
(1)求和乙样本直方图中的值;
(2)试估计该校物理方向的学生本次模拟测试数学成绩的平均值和历史方向的学生本次模拟测试数学成绩的中位数(同一组中的数据用该组区间中点值为代表).
(3)采用分层抽样的方法从甲样本数据中分数在和的学生中抽取6人,并从这6人中任取2人,求这两人分数都在中的概率.
20.2023年为普及航天知识,某校开展了“航天知识竞赛”活动,现从参加该竞赛的学生中随机抽取了80名,统计他们的成绩(满分100分),其中成绩不低于80分的学生被评为“航天达人”,将数据整理后绘制成如图所示的频率分布直方图.
(1)若该中学参加这次竞赛的共有3000名学生,试估计全校这次竞赛中“航天达人”的人数;
(2)估计参加这次竞赛的学生成绩的第75百分位数;
(3)若在抽取的80名学生中,利用分层随机抽样的方法从成绩不低于70分的学生中随机抽取6人,再从6人中选择2人作为学生代表,求被选中的2人均为航天达人的概率.
21.某中学高三年级某班50名学生期中考试数学成绩的频率分布直方图如图所示,成绩分组区间为:,,,,,,.其中,且.物理成绩统计如表.(说明:数学满分150分,物理满分100分)
物理成绩统计表
分组
频数 6 9 20 10 5
(1)根据频率分布直方图,请估计数学成绩的平均分(同一组数据用该区间的中点值代表);
(2)若数学成绩不低于140分的为“优”,物理成绩不低于90分的为“优”,已知本班中至少有一个“优”的同学总数为6人,从数学成绩为“优”的同学中随机抽取2人,求两人恰好均为物理成绩为“优”的概率.
第1页 共4页 ◎ 第2页 共4页
第1页 共4页 ◎ 第2页 共4页
参考答案:
1.C
【分析】记从甲袋中摸出一个红球的事件为,从乙袋中摸出一个红球的事件为,根据互斥和对立事件的定义分析判断AC;根据独立事件概率乘法公式以及互斥事件概率求法分析判断BD.
【详解】记从甲袋中摸出一个红球的事件为,从乙袋中摸出一个红球的事件为,
可知,相互独立,
于是:,
由此可得:可能同时发生,A错误;互为对立事件,C正确;
因为,所以,B错误;
因为,所以,D错误.
故选:C.
2.C
【分析】利用古典概型计算公式先列举出所有基本事件数,再求出是孪生素数的事件数即可求得结果.
【详解】不超过10的正奇数有,共5个,从中随机抽取2个,
共有,10种情况,
其中孪生素数有,共2种情况,
由古典概型可得这2个奇数是孪生素数的概率为.
故选:C.
3.C
【分析】根据互斥、相互独立事件的乘法公式对选项一一判断即可得出答案.
【详解】依题意甲、乙两人所选选项有如下情形:
①有一个选项相同,②两个选项相同,③两个选项不相同,
所以,,,,
因为事件与事件互斥,所以,又,
所以事件M与事件N不相互独立,故A错误;
,故B错误;
由,则事件M与事件Y相互独立,故C正确;
因为事件N与事件Y互斥,所以,又,
所以事件N与事件Y不相互独立,故D错误.
故选:C.
【点睛】关键点点睛:本题的关键点在于先求出,,,,再根据互斥、相互独立事件的乘法公式对选项一一判断即可.
4.B
【分析】借助频率估计概率后,结合相互独立事件的概率公式计算即可得.
【详解】甲来徐州旅游的概率约为,乙来徐州旅游的概率约为,
丙来徐州旅游的概率约为,
则三人都没有来徐州旅游的概率约为,
故三个人中至少有1人来徐州旅游的概率约为.
故选:B.
5.A
【分析】将频率视为概率,分别计算汽车,选择公路1和公路2按时到达的概率,以此判断最佳路径.
【详解】频率分布表如下:
所用时间天数 10 11 12 13
通过公路1的频率
通过公路2的频率
设,分别表示事件“汽车A选择公路1时在约定时间内将货物运至城市乙”和“汽车A选择公路2时在约定时间内将货物运至城市乙”,
,分别表示事件“汽车B选择公路1时在约定时间内将货物运至城市乙”和“汽车B选择公路2时在定时间内将货物运至城市乙”,
以频率估计概率得,,,,
所以汽车A和汽车B选择的最佳路径分别为公路1和公路2.
故选:.
6.C
【分析】根据分层抽样、平均数、古典概率等知识确定正确答案.
【详解】A选项,抽查的样本中女职工人数为,A选项正确.
B选项,男性平均体重为63千克;女性平均体重为54千克,
所以该单位男职工的体重普遍比女职工较重,B选项正确.
C选项,估计该单位职工平均体重为,C选项错误.
D选项,每一位男或女职工被抽中的可能性均为,D选项正确.
故选:C
7.A
【分析】计算出该班学生中既参加了羽毛球运动又参加了乒乓球运动的人数,利用古典概型概率计算公式计算即可.
【详解】依题意,该班学生中既参加了羽毛球运动又参加了乒乓球运动有:
(名),
故从该班随机抽取一名同学,
该同学既参加了羽毛球运动又参加了乒乓球运动的概率为,
故选:A.
8.C
【分析】根据给定条件,求出周一至周五任选两天的试验的样本空间,再求出连续两天的事件含有的样本点,进而求出古典概率.
【详解】令周一至周五的5天依次为1,2,3,4,5,
则周一至周五任选两天的样本空间,共10个样本点,
连续两天的事件,共4个样本点,
所以该校的同学甲连续两天为父母捶背的概率为.
故选:C
9.AD
【分析】
利用古典概型的概率计算各事件概率,再根据独立事件概率的关系依次判断即可.
【详解】依题意基本事件总数为个,
“第一次取出的球的数字是”的基本事件有个,
“第二次取出的球的数字是”的基本事件有个,
“两次取出的球的数字之和为”的基本事件有共个,
“两次取出的球的数字之和为”的基本事件有共个,
所以(丙),(丁);(甲)(乙),故A正确,B错误;
又同时满足事件甲、丁的基本事件有共个,同时满足事件乙、丙的基本事件有共个,
所以(乙丙)(乙)(丙),所以乙与丙不相互独立,故C错误;
所以(甲丁)(甲)(丁),所以甲与丁相互独立,故D正确;
故选:AD.
10.ABC
【分析】画出树状图,结合图形及古典概型逐项分析判断.
【详解】画出树状图,结合图形
结合树状图可知:,
对于选项A:可知,故A正确;
对于选项B: 均有,故B正确;
对于选项C:因为,不经过数字5的路线有9条,所以,故C正确;
对于选项D:因为,所以,故D错误;
故选:ABC.
11.BD
【分析】直接由平均数、方差、百分位数及对立事件的概念,逐一对各个选项分析判断,即可得出结果.
【详解】对于选项A,甲机构测评分数的平均分,
乙机构测评分数的平均分,所以选项A错误,
对于选项B,甲机构测评分数的方差,
,所以选项B正确,
对于选项C,乙机构测评分数从小排到大为:91,92,93,94,95,
又,所以乙机构测评分数的第一四分位数为92,所以选项C错误,
对于选项D,因为甲机构测评分数中有且仅有2个测评分数超过平均分,由对立事件的定义知,事件互为对立事件,所以选项D正确,
故选:BD.
12.ACD
【分析】A选项,根据频率之和为列出方程,求出;B选项,用中间值作代表,求出班和B班该月平均每天产生的饮料瓶个数估计值,比较出结果;C选项,利用百分位数的定义求出,,故C正确;D选项,结合频率分布直方图得到该校学生月份产生饮料瓶数在的频率为0.2,从而求出D正确.
【详解】对于A选项,由,解得,A正确;
对于B选项,班该月平均每天产生的饮料瓶个数估计为,
班该月平均每天产生的饮料瓶个数估计为,
因为,所以班该月平均每天产生的饮料瓶比班更少,B错误;
对于C选项,,,
故班月产生饮料瓶数的上四分位数位于内,
故,解得,
,
,
故班月产生饮料瓶数的上四分位数位于内,
故,解得,故,C正确;
对于D选项,班和班月产生饮料瓶数在的频率均为,
故该校学生月份产生饮料瓶数在的频率也为,
,所以该校约有人月份产生饮料瓶数在之间,D正确.
故选:ACD
13./
【分析】
考虑先赢四场比赛的队伍获胜,甲队已经赢了两场,故只需再先赢两场则获胜,分析得到甲在随后进行的场次可以有两场连胜,也可输一场赢两场(含两种情况),还可以输两场赢两场(含三种情况),分别计算概率,再利用互斥事件的概率加法公式即得.
【详解】
由题意得甲、乙两队获胜的概率均为,且最多再进行四场比赛,最少再进行两场比赛.
则①再进行两场比赛甲队获胜的概率为;
②再进行三场比赛甲队获胜的概率为;
③再进行四场比赛甲队获胜的概率为,
由互斥事件的概率加法公式,可得最终甲队获胜的概率为.
故答案为.
14.
【分析】
利用条件概率的计算公式可求
【详解】表示“取到的两个数为偶数且和为偶数”,,
而,故,
故答案为:.
15.
【分析】先根据左边的频率分布直方图得到,再根据右边的频率分布直方图可得.
【详解】依题可知,左边图形第一个小矩形的面积为,所以,
所以,解得:,
由右边的频率分布直方图可得.
故答案为:
16.
【分析】每关得到的最大点数为,令,利用作差法可求得数列单调性,由此可确定当时,,从而得到结论;分别计算该人通过第一、第二和第三关的概率,根据独立事件概率乘法公式可求得结果.
【详解】若每次抛掷一颗骰子都能得到最大点数点,则第关抛掷的点数和为,
令,则,
则当时,数列单调递增;当时,数列单调递减;
又,,,
当时,,则某人在这项游戏中最多能过关;
该人第一关所有可能的结果为,则通过第一关的概率;
该人第二关所有可能的结果有种,则不能过关的基本事件个数为的正整数解的个数,则有种,
通过第二关的概率;
该人第三关所有可能的结果有种,则不能过关的基本事件个数为的正整数解得个数,则有种,
通过第三关的概率;
连过前三关的概率.
故答案为:;.
17.(1),
(2)
【分析】
(1)利用频率分布直方图中各个小矩形的面积之和为可求出的值,再利用百分位数的定义求这组数据的第百分位数即可;
(2)利用古典概型的概率公式求解.
【详解】(1)
由频率分布直方图可知,,
解得,
因为,,
所以这组数据的第百分位数位于,设其为,
则,
解得,即这组数据的第百分位数为;
(2)
由题可知,从分数在内的学生中抽取人,记为,,
则分数在内的学生中抽取人,记为,,,,
从中任选人,则所有可能结果有:,,,,,,,,
,,,,,,共个,
满足这人成绩之差的绝对值大于分的有,,,,,,,共个,
故所求的概率.
18.(1)平均数76,中位数约为76.67.
(2).
【分析】
(1)利用频率分布直方图,根据平均数和中位数的计算方法即可求得答案;
(2)确定成绩为的学生中成绩在和内的人数比例,即可确定抽查的5人中各组抽的人数,列举出抽取的人中任选取人的所有可能情况,再列出选取的人中恰有人成绩在内的情况,根据古典概型的概率公式即可求得答案.
【详解】(1)
,
设中位数为,因为前组的频率之和为,
而前2组的频率之和为,所以,
由,
解得:,
故可估计这500名学生初赛成绩的中位数约为;
(2)
根据分层抽样,由频率分布直方图知成绩在和内的人数比例为,
所以抽取的5人中,成绩在内的有人,记为,;
成绩在内的有人,记为,,,
从5人中任意选取2人,有,,,,,,,,,,共10种可能;
其中选取的2人中恰有1人成绩在区间内的有,,,,,,共6种可能;
故所求的概率为.
19.(1);;
(2)平均值81.5,中位数82;
(3)
【分析】
(1)根据频率定义即可求出,再根据小矩形面积和为1即可求出值;
(2)根据平均数和中位数定义计算即可;
(3)列出所有情况和满足题意的情况,再利用古典概率公式即可.
【详解】(1)由直方图可知,乙样本中数据在的频率为,
则,解得;
由乙样本数据直方图可知,,
解得;
(2)甲样本数据的平均值估计值为
,
乙样本数据直方图中前3组的频率之和为,
前4组的频率之和为,
所以乙样本数据的中位数在第4组,设中位数为,
,
解得,所以乙样本数据的中位数为82.
(3)由频率分布直方图可知从分数在和的学生中分别抽取2人和4人,
将从分数在中抽取的2名学生分别记为,从分数在中抽取的4名学生分别记为,
则从这6人中随机抽取2人的基本事件有
,共15个,
所抽取的两人分数都在中的基本事件有6个,所以所求概率为.
20.(1)
(2)
(3)
【分析】(1)由频率分布直方图求出成绩在内的频率,即可估计人数;
(2)根据百分位数计算规则计算可得;
(3)先按照分层抽样求出各层人数,再利用列举法结合古典概型即可得解.
【详解】(1)由频率分布直方图可知,
成绩在内的频率为,
则估计全校这次竞赛中“航天达人”的人数约为人;
(2)由频率分布直方图可知,成绩在内的频率为,
成绩在内的频率为,
成绩在内的频率为,
成绩在内的频率为,
成绩在内的频率为,
所以成绩在分以下的学生所占的比例为,
成绩在分以下的学生所占的比例为,
所以成绩的分位数一定在内,即,
因此估计参加这次竞赛的学生成绩的分位数为;
(3)因为,,,
所以从成绩在,,内的学生中分别抽取了人,人,人,
其中有人为航天达人,设为,
有人不是航天达人,设为,
则从6人中选择2人作为学生代表,
有,
共种,
其中2人均为航天达人为共种,
所以被选中的2人均为航天达人的概率为.
21.(1)117.8分;
(2).
【分析】(1)计算,再利用频率分布直方图估计平均数.
(2)计算得到两科均为“优”的人数为3人,设两科均为“优”的同学为,物理成绩不是“优”的同学为B,列出所有情况,统计满足条件的情况,得到概率.
【详解】(1)依题意,,
解得,
所以数学成绩的平均分:
.
(2)数学成绩为“优”的同学有人,物理成绩为“优”有5人,
因为至少有一个“优”的同学总数为6名同学,则两科均为“优”的人数为3人.
设两科均为“优”的同学为,物理成绩不是“优”的同学为B,
则从4人中随机抽取2人的所有情况有:,
符合题意的情况有:,
故两人恰好均为物理成绩“优”的概率.
答案第1页,共2页
答案第1页,共2页
