江苏省苏州高新区实验初级中学2023-2024学年九年级下学期3月月考数学试题(PDF版无答案)
文档属性
| 名称 | 江苏省苏州高新区实验初级中学2023-2024学年九年级下学期3月月考数学试题(PDF版无答案) |  | |
| 格式 | |||
| 文件大小 | 334.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-21 19:06:32 | ||
图片预览

文档简介
2023- 2024学年苏州新区实验九年级下学期月考数学试题
本试卷由单选题、填空题和解答题三大题组成,共 27题,满分 130分,考试用时 120分钟.
一、单选题 (本题满分 24分,共 8小题,每小题 3分)
1.-5的相反数是 ( )
A. - 5 B. 5 C. 15 D. -
1
5
2.若把一个数用科学记数法表示后为-3.96× 105,则这个数是 ( )
A. - 39600 B. - 396000 C. 0.0000396 D. 0.00000396
3.下列计算正确的是 ( )
A. 2m+ 3n= 5mn B. - a2b+ ba2= 0 C. x2+ 2x2= 3x4 D. 3(a+ b) = 3a+ b
4.学校篮球队队员进行定点投篮训练,每人投篮 10次,其中 5名队员投中的次数分别是:6,7,6,9,8,则这组数
据的众数和中位数分别是 ( )
A. 6,6 B. 7,6 C. 6,7 D. 7,8
5.将抛物线 y=-x2向右平移 3个单位,再向上平移 4个单位,得到的抛物线是 ( )
A. y=- (x- 3)2+ 4 B. y=- (x- 3)2+ 4 C. y=- (x+ 3)2- 4 D. y=- (x+ 3)2- 4
6.如图,⊙O是ΔABC的外接圆,∠A= 72°.过点O作BC的垂线交BC于点D,连接BD,则∠D的度数为
( )
A. 64° B. 54° C. 46° D. 36°
7.若一元二次方程 x2- 2x-m= 0无实数根,则二次函数 y= (m+ 1)x2+m- 1的图象必经过第 ( )象限.
A.一、二象限 B.三、四象限 C.一、二、三象限 D.一、三、四象限
8.若一个点的坐标满足 (k,2k),我们将这样的点定义为“倍值点”.若关于 x的二次函数 y= (t+ 1)x2+ (t+ 2)x
+ s(s,t为常数,t≠-1)总有两个不同的倍值点,则 s的取值范围是 ( )
A. s<-1 B. s< 0 C. 0< s< 1 D. - 1< s< 0
二、填空题 (本题满分 24分,共 8小题,每小题 3分)
9. y= x-1函数 x-2 在实数范围内有意义的条件是 .
10.分解因式:xy2- 4x= .
11.一个圆锥的底面圆半径是 1,母线长是 3,则此圆锥的侧面积为 .
12.如图,抛物线 y= ax2+ bx+ c与 x轴相交于点A(1,0)、点 B(3,0),与 y轴相交于点 C,点D在抛物线上,当
CD x轴时,CD= .
6 (第12题图) (第13题图)(第 题图)
13.如图,一次函数 y1=
k
k1x+ b与反比例函数 y = 22 x 的图象相交于A,B两点,点A的横坐标为 2,点B的横坐标
- k为 1,则不等式 k1x+ b< 2x 的解集是 .
初三数学 第1页 共1页
{#{QQABbYwAggiIAIAAAQgCAQEiCkIQkAGCAIoORBAMIAAAyRFABAA=}#}
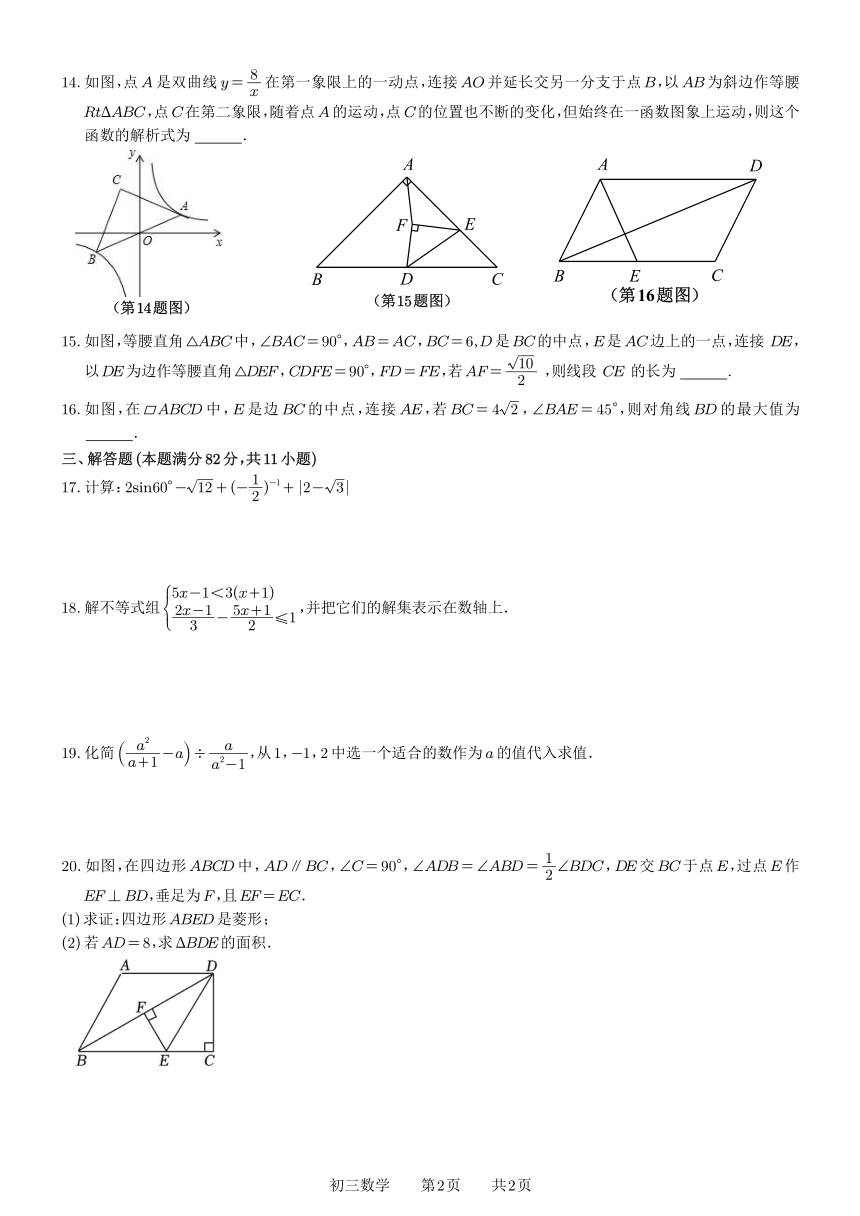
14.如图,点A是双曲线 y= 8x 在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰
RtΔABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个
函数的解析式为 .
A A D
F E
B D C B E C
(第14题图) (第15题图)
(第16题图)
15.如图,等腰直角△ABC中,∠BAC= 90°,AB=AC,BC= 6,D是BC的中点,E是AC边上的一点,连接 DE,
以DE为边作等腰直角△DEF,CDFE= 90° FD=FE 10, ,若AF= 2 ,则线段 CE 的长为 .
16.如图,在 ABCD中,E是边 BC的中点,连接 AE,若 BC = 4 2,∠BAE = 45°,则对角线 BD的最大值为
.
三、解答题 (本题满分 82分,共 11小题)
17.计算:2sin60° - 12+ (- 1 )-12 + 2- 3
18.解不等式组 5x-1<3(x+1) 2x-1 - 5x+1 ≤ ,并把它们的解集表示在数轴上.3 2 1
2
19. a化简 a+1 -a ÷
a
,从 1,-1,2中选一个适合的数作为 a的值代入求值.
a2-1
20. 1如图,在四边形ABCD中,AD BC,∠C= 90°,∠ADB=∠ABD= 2 ∠BDC,DE交 BC于点 E,过点 E作
EF⊥BD,垂足为F,且EF=EC.
(1)求证:四边形ABED是菱形;
(2)若AD= 8,求ΔBDE的面积.
初三数学 第2页 共2页
{#{QQABbYwAggiIAIAAAQgCAQEiCkIQkAGCAIoORBAMIAAAyRFABAA=}#}
21.一个不透明的箱子里装有 1个白色小球和若干个红色小球,每个小球除颜色外其他完全相同,每次把箱子里的
小球摇匀后随机摸出一个小球,记下颜色后再放回箱子里,通过大量重复实验后,发现摸到白色小球的频率稳
定于 0.25左右.
(1)请你估计箱子里红色小球的个数;
(2)现从该箱子里摸出 1个小球,记下颜色后放回箱子里,摇匀后,再摸出 1个小球,求两次摸出的小球颜色恰好不
同的概率 (用画树状图或列表的方法).
22.快递使我们的生活更加便捷,可以说,快递改变了我们的生活.为了解我国的快递业务情况,我们收集了 2022
年 11月全国 31个省的快递业务数量 (单位:亿件)的数据,并对数据进行了整理、描述和分析,给出如下信息:
a. 2022年 11月快递业务量排在前 3位的省的数据分别为:275.2,225,74.8,
b.其余 28个省份 2022年 11月的快递业务数量的数据的频数分布图如图:
c.2022年 11月的快递业务数量的数据在 10≤ x< 20这一组的是:10.3,11,15.5,16.3,17.8,根据以上信息,回答
下列问题:
(1)补全条形统计图;
(2)2022年 11月的 31个省的快递业务数量的中位数为 ;
(3) 若设图中 28个省份平均数为 x1,方差为 s2 2 2 21;设 31个省份的平均数为 x,方差为 s ,则 x1 x,s1 s
(填“>”“ =”或“<”).
23. k k如图,直线 y= x与双曲线 y= x (x> 0)交于点A.将直线 y= x向右平移 4个单位长度后,与双曲线 y= x
(x> 0)交于点B,与 x轴交于点C.
(1)若OA= 2BC,则 k的值;
(2) 8在(1)的条件下,若点A的横坐标为 3 ,求S△AOB.
初三数学 第3页 共3页
{#{QQABbYwAggiIAIAAAQgCAQEiCkIQkAGCAIoORBAMIAAAyRFABAA=}#}
24.加强劳动教育,落实五育并举.某中学在当地政府的支持下,建成了一处劳动实践基地. 2024年计划将其中
1000m2的土地全部种植甲乙两种蔬菜.经调查发现:甲种蔬菜种植成本 y(单位:元 /m2)与其种植面积 x(单
位:m2)的函数关系如图所示,其中 200≤ x≤ 700,乙种蔬菜的种植成本为 50元 /m2.
(1)当 x为多少m2时,y是 35元 /m2;
(2)设 2024年甲乙两种蔬菜总种植成本为W元,如何分配两种蔬菜的种植面积,使W最小?
25.本题满分 8分)如图,⊙O是等腰三角形ABC的外接圆,AB=AC,延长BC到点D,使CD=AC,连接AD
交⊙O于点E,连接BE与AC 交于点F.
(1)判断BE是否平分∠ABC,并说明理由:
(2)若AE= 6,BE= 8,求EF的长,
初三数学 第4页 共4页
{#{QQABbYwAggiIAIAAAQgCAQEiCkIQkAGCAIoORBAMIAAAyRFABAA=}#}
26.综合与实践:
数学模型可以用来解决一类问题,是数学应用的基本途径.通过探究图形的变化规律,再结合其他数学知识的内
在联系,最终可以获得宝贵的数学经验,并将其运用到更广阔的数学天地.
(1)发现问题:如图 1,在 ΔABC和 ΔAEF中,AB=AC,AE=AF,∠BAC=∠EAF= 30°,连接 BE,CF,延长
BE交CF于点D.则BE与CF的数量关系: ,∠BDC= °;
(2)类比探究:如图 2,在 ΔABC和 ΔAEF中,AB=AC,AE=AF,∠BAC=∠EAF= 120°,连接BE,CF,延长
BE,FC交于点D.请猜想BE与CF的数量关系及∠BDC的度数,并说明理由;
(3)拓展延伸:如图 3,ΔABC和ΔAEF均为等腰直角三角形,∠BAC=∠EAF= 90°,连接BE,CF,且点B,E,F
在一条直线上,过点A作AM⊥BF,垂足为点M.则BF,CF,AM之间的数量关系: ;
(4)实践应用:正方形ABCD中,AB= 4,若平面内存在点P满足∠BPD= 90°,PD= 2,则SΔABP= .
27.已知 (x1,y1),(x2,y2)是抛物线C1:y=- 1 24 x + bx(b为常数)上的两点,当 x1+ x2= 0时,总有 y1= y2.
(1)求 b的值;
(2)将抛物线C1平移后得到抛物线C :y=- 12 4 (x-m)
2+ 1(m> 0).
当 0≤ x≤ 2时,探究下列问题:
①若抛物线C1与抛物线C2有一个交点,求m的取值范围;
②设抛物线C2与 x轴交于A,B两点,与 y轴交于点C,抛物线C2的顶点为点E,ΔABC外接圆的圆心为点F.如
果对抛物线C1上的任意一点P,在抛物线C2上总存在一点Q,使得点P、Q的纵坐标相等.求EF长的取值范围.
初三数学 第5页 共5页
{#{QQABbYwAggiIAIAAAQgCAQEiCkIQkAGCAIoORBAMIAAAyRFABAA=}#}
本试卷由单选题、填空题和解答题三大题组成,共 27题,满分 130分,考试用时 120分钟.
一、单选题 (本题满分 24分,共 8小题,每小题 3分)
1.-5的相反数是 ( )
A. - 5 B. 5 C. 15 D. -
1
5
2.若把一个数用科学记数法表示后为-3.96× 105,则这个数是 ( )
A. - 39600 B. - 396000 C. 0.0000396 D. 0.00000396
3.下列计算正确的是 ( )
A. 2m+ 3n= 5mn B. - a2b+ ba2= 0 C. x2+ 2x2= 3x4 D. 3(a+ b) = 3a+ b
4.学校篮球队队员进行定点投篮训练,每人投篮 10次,其中 5名队员投中的次数分别是:6,7,6,9,8,则这组数
据的众数和中位数分别是 ( )
A. 6,6 B. 7,6 C. 6,7 D. 7,8
5.将抛物线 y=-x2向右平移 3个单位,再向上平移 4个单位,得到的抛物线是 ( )
A. y=- (x- 3)2+ 4 B. y=- (x- 3)2+ 4 C. y=- (x+ 3)2- 4 D. y=- (x+ 3)2- 4
6.如图,⊙O是ΔABC的外接圆,∠A= 72°.过点O作BC的垂线交BC于点D,连接BD,则∠D的度数为
( )
A. 64° B. 54° C. 46° D. 36°
7.若一元二次方程 x2- 2x-m= 0无实数根,则二次函数 y= (m+ 1)x2+m- 1的图象必经过第 ( )象限.
A.一、二象限 B.三、四象限 C.一、二、三象限 D.一、三、四象限
8.若一个点的坐标满足 (k,2k),我们将这样的点定义为“倍值点”.若关于 x的二次函数 y= (t+ 1)x2+ (t+ 2)x
+ s(s,t为常数,t≠-1)总有两个不同的倍值点,则 s的取值范围是 ( )
A. s<-1 B. s< 0 C. 0< s< 1 D. - 1< s< 0
二、填空题 (本题满分 24分,共 8小题,每小题 3分)
9. y= x-1函数 x-2 在实数范围内有意义的条件是 .
10.分解因式:xy2- 4x= .
11.一个圆锥的底面圆半径是 1,母线长是 3,则此圆锥的侧面积为 .
12.如图,抛物线 y= ax2+ bx+ c与 x轴相交于点A(1,0)、点 B(3,0),与 y轴相交于点 C,点D在抛物线上,当
CD x轴时,CD= .
6 (第12题图) (第13题图)(第 题图)
13.如图,一次函数 y1=
k
k1x+ b与反比例函数 y = 22 x 的图象相交于A,B两点,点A的横坐标为 2,点B的横坐标
- k为 1,则不等式 k1x+ b< 2x 的解集是 .
初三数学 第1页 共1页
{#{QQABbYwAggiIAIAAAQgCAQEiCkIQkAGCAIoORBAMIAAAyRFABAA=}#}
14.如图,点A是双曲线 y= 8x 在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰
RtΔABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个
函数的解析式为 .
A A D
F E
B D C B E C
(第14题图) (第15题图)
(第16题图)
15.如图,等腰直角△ABC中,∠BAC= 90°,AB=AC,BC= 6,D是BC的中点,E是AC边上的一点,连接 DE,
以DE为边作等腰直角△DEF,CDFE= 90° FD=FE 10, ,若AF= 2 ,则线段 CE 的长为 .
16.如图,在 ABCD中,E是边 BC的中点,连接 AE,若 BC = 4 2,∠BAE = 45°,则对角线 BD的最大值为
.
三、解答题 (本题满分 82分,共 11小题)
17.计算:2sin60° - 12+ (- 1 )-12 + 2- 3
18.解不等式组 5x-1<3(x+1) 2x-1 - 5x+1 ≤ ,并把它们的解集表示在数轴上.3 2 1
2
19. a化简 a+1 -a ÷
a
,从 1,-1,2中选一个适合的数作为 a的值代入求值.
a2-1
20. 1如图,在四边形ABCD中,AD BC,∠C= 90°,∠ADB=∠ABD= 2 ∠BDC,DE交 BC于点 E,过点 E作
EF⊥BD,垂足为F,且EF=EC.
(1)求证:四边形ABED是菱形;
(2)若AD= 8,求ΔBDE的面积.
初三数学 第2页 共2页
{#{QQABbYwAggiIAIAAAQgCAQEiCkIQkAGCAIoORBAMIAAAyRFABAA=}#}
21.一个不透明的箱子里装有 1个白色小球和若干个红色小球,每个小球除颜色外其他完全相同,每次把箱子里的
小球摇匀后随机摸出一个小球,记下颜色后再放回箱子里,通过大量重复实验后,发现摸到白色小球的频率稳
定于 0.25左右.
(1)请你估计箱子里红色小球的个数;
(2)现从该箱子里摸出 1个小球,记下颜色后放回箱子里,摇匀后,再摸出 1个小球,求两次摸出的小球颜色恰好不
同的概率 (用画树状图或列表的方法).
22.快递使我们的生活更加便捷,可以说,快递改变了我们的生活.为了解我国的快递业务情况,我们收集了 2022
年 11月全国 31个省的快递业务数量 (单位:亿件)的数据,并对数据进行了整理、描述和分析,给出如下信息:
a. 2022年 11月快递业务量排在前 3位的省的数据分别为:275.2,225,74.8,
b.其余 28个省份 2022年 11月的快递业务数量的数据的频数分布图如图:
c.2022年 11月的快递业务数量的数据在 10≤ x< 20这一组的是:10.3,11,15.5,16.3,17.8,根据以上信息,回答
下列问题:
(1)补全条形统计图;
(2)2022年 11月的 31个省的快递业务数量的中位数为 ;
(3) 若设图中 28个省份平均数为 x1,方差为 s2 2 2 21;设 31个省份的平均数为 x,方差为 s ,则 x1 x,s1 s
(填“>”“ =”或“<”).
23. k k如图,直线 y= x与双曲线 y= x (x> 0)交于点A.将直线 y= x向右平移 4个单位长度后,与双曲线 y= x
(x> 0)交于点B,与 x轴交于点C.
(1)若OA= 2BC,则 k的值;
(2) 8在(1)的条件下,若点A的横坐标为 3 ,求S△AOB.
初三数学 第3页 共3页
{#{QQABbYwAggiIAIAAAQgCAQEiCkIQkAGCAIoORBAMIAAAyRFABAA=}#}
24.加强劳动教育,落实五育并举.某中学在当地政府的支持下,建成了一处劳动实践基地. 2024年计划将其中
1000m2的土地全部种植甲乙两种蔬菜.经调查发现:甲种蔬菜种植成本 y(单位:元 /m2)与其种植面积 x(单
位:m2)的函数关系如图所示,其中 200≤ x≤ 700,乙种蔬菜的种植成本为 50元 /m2.
(1)当 x为多少m2时,y是 35元 /m2;
(2)设 2024年甲乙两种蔬菜总种植成本为W元,如何分配两种蔬菜的种植面积,使W最小?
25.本题满分 8分)如图,⊙O是等腰三角形ABC的外接圆,AB=AC,延长BC到点D,使CD=AC,连接AD
交⊙O于点E,连接BE与AC 交于点F.
(1)判断BE是否平分∠ABC,并说明理由:
(2)若AE= 6,BE= 8,求EF的长,
初三数学 第4页 共4页
{#{QQABbYwAggiIAIAAAQgCAQEiCkIQkAGCAIoORBAMIAAAyRFABAA=}#}
26.综合与实践:
数学模型可以用来解决一类问题,是数学应用的基本途径.通过探究图形的变化规律,再结合其他数学知识的内
在联系,最终可以获得宝贵的数学经验,并将其运用到更广阔的数学天地.
(1)发现问题:如图 1,在 ΔABC和 ΔAEF中,AB=AC,AE=AF,∠BAC=∠EAF= 30°,连接 BE,CF,延长
BE交CF于点D.则BE与CF的数量关系: ,∠BDC= °;
(2)类比探究:如图 2,在 ΔABC和 ΔAEF中,AB=AC,AE=AF,∠BAC=∠EAF= 120°,连接BE,CF,延长
BE,FC交于点D.请猜想BE与CF的数量关系及∠BDC的度数,并说明理由;
(3)拓展延伸:如图 3,ΔABC和ΔAEF均为等腰直角三角形,∠BAC=∠EAF= 90°,连接BE,CF,且点B,E,F
在一条直线上,过点A作AM⊥BF,垂足为点M.则BF,CF,AM之间的数量关系: ;
(4)实践应用:正方形ABCD中,AB= 4,若平面内存在点P满足∠BPD= 90°,PD= 2,则SΔABP= .
27.已知 (x1,y1),(x2,y2)是抛物线C1:y=- 1 24 x + bx(b为常数)上的两点,当 x1+ x2= 0时,总有 y1= y2.
(1)求 b的值;
(2)将抛物线C1平移后得到抛物线C :y=- 12 4 (x-m)
2+ 1(m> 0).
当 0≤ x≤ 2时,探究下列问题:
①若抛物线C1与抛物线C2有一个交点,求m的取值范围;
②设抛物线C2与 x轴交于A,B两点,与 y轴交于点C,抛物线C2的顶点为点E,ΔABC外接圆的圆心为点F.如
果对抛物线C1上的任意一点P,在抛物线C2上总存在一点Q,使得点P、Q的纵坐标相等.求EF长的取值范围.
初三数学 第5页 共5页
{#{QQABbYwAggiIAIAAAQgCAQEiCkIQkAGCAIoORBAMIAAAyRFABAA=}#}
同课章节目录
