2024学年浙江省温州市瑞安塘下片区六校九年级下学期入学检测 数学试卷(含答案)
文档属性
| 名称 | 2024学年浙江省温州市瑞安塘下片区六校九年级下学期入学检测 数学试卷(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-21 19:42:38 | ||
图片预览



文档简介
2023学年第二学期九年级入学检测
数学试卷
亲爱的同学:
欢迎你参加考试!做题时要认真审题,积极思考,细心答题,发挥你的最佳水平.
答卷时,请注意以下几点:
1.全卷满分为120分,考试时间120分钟.
2.全卷由试题卷和答题卷两部分组成,请将答案写在答题卷相应的位置,写在试题卷上无效.
3.书写时字迹要工整,清晰,请勿使用涂改液、修正带、计算器等.祝你成功!
一、选择题(本题有10小题,每小题3分,共30分.每小题只有一个选项是正确的,不选、多选、错选均不给分)
1.如图,数轴上点表示的数绝对值最小的是( )
(第1题)
A. B. C. D.
阅读下列材料,完成第2,3题.
【材料】随着新媒体的发展,更好地推动了全民阅读,一些学者、作家、文化文艺名人等担任“领读人”,通过直播、短视频以及图文等形式,利用新媒体平台助力大众阅读.经典名著依旧是大众推崇的书目,经统计四大名著相关读书视频总播放量已超过3亿,具体数据如图1所示.
图1
2.四大名著中,哪一本名著的相关视频最受欢迎( )
A.《红楼梦》 B.《西游记》 C.《三国演义》 D.《水浒传》
3.四大名著相关读书视频总播放量中,《西游记》的播放量为93000000,请将这个数字用科学记数法表示为( )
A. B. C. D.
4.下列计算正确的是( )
A. B. C. D.
5.剪纸是中国古代最古老的民间艺术之一,其中蕴含着图形的变换.如图是一张蕴含着轴对称变换的蝴蝶剪纸,点与点对称,点与点对称,将其放置在直角坐标系中,点,,的坐标分别为,,,则点的坐标为( )
(第5题)
A. B. C. D.
6.如图,点是的重心,过点作的平行线,分别交,于点,若,则的长为( )
(第6题)
A.2 B.3 C.4 D.5
7.某人买了甲、乙两个品牌的衬衣共件,其中甲品牌衬衣比乙品牌衬衣多5件.已知甲品牌衬衣的单价为120元,乙品牌衬衣的单价为90元,则买这件衬衣共需付款( )
A. B. C. D.
8.一组7个数据分别为,,,,,,.若去掉一个数据,平均数不变,则下列说法正确的是( )
A.中位数与众数都不变 B.众数与方差都不变
C.中位数与极差都不变 D.众数与极差都不变
9.已知二次函数,当时,则( )
A.若时,函数有最小值 B.若时,函数有最小值
C.若时,函数有最小值 D.若时,函数有最小值
10.由四个全等的直角三角形和一个小正方形组成的大正方形如图所示.点是正方形的中心,连结并延长交于点,连结,记的面积为,正方形的面积为.若,则的值为( )
(第10题)
A. B. C. D.
二、填空题(本题有6小题,每小题4分,共24分)
11.计算:______.
12.不等式的解是______.
13.某班45名学生体重达标情况(单位:人)如下表所示,在该班中随机抽取一名学生,其体重为标准的概率是______.
体重 偏瘦 标准 超重 肥胖
人数 3 36 4 2
14.一扇形的圆心角为,弧长为,则该扇形的半径为______.
15.如图,内有一Rt,,,点在圆上,边经过圆心.是平移后的图像,点,的对应点,在上,点的对应点在外,若与相切,连结,则______ .
(第15题)
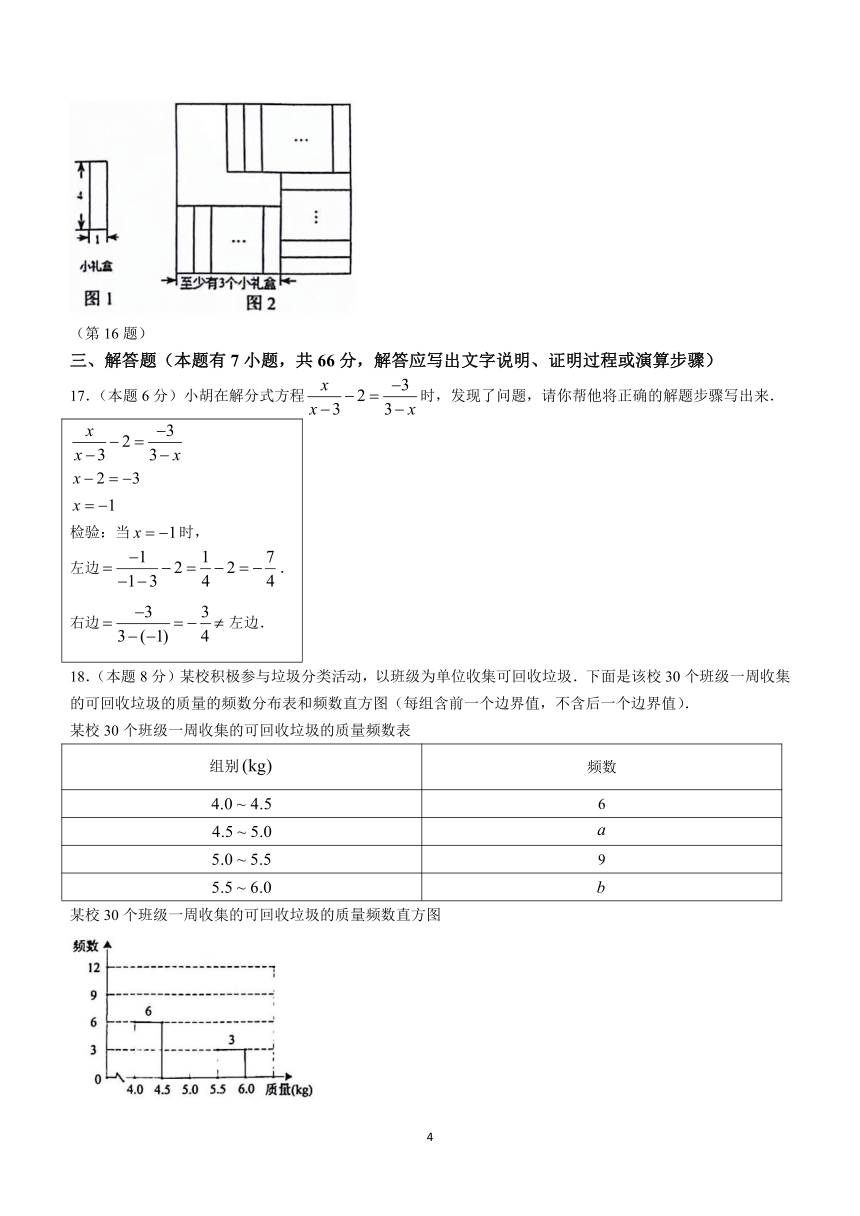
16.如图1所示的长方形是一种小礼盒的俯视图,其长为4,宽为1.现将若干个小礼盒如图2所示摆放到一个俯视图为正方形的大礼盒中,若留空的部分(阴影部分)的面积是整个正方形面积的,则大正方形边长最小是______.
(第16题)
三、解答题(本题有7小题,共66分,解答应写出文字说明、证明过程或演算步骤)
17.(本题6分)小胡在解分式方程时,发现了问题,请你帮他将正确的解题步骤写出来.
检验:当时,左边.右边左边.
18.(本题8分)某校积极参与垃圾分类活动,以班级为单位收集可回收垃圾.下面是该校30个班级一周收集的可回收垃圾的质量的频数分布表和频数直方图(每组含前一个边界值,不含后一个边界值).
某校30个班级一周收集的可回收垃圾的质量频数表
组别 频数
6
9
某校30个班级一周收集的可回收垃圾的质量频数直方图
(1)求和的值,并补全频数直方图.
(2)已知收集的可回收垃圾以0.8元被回收,该校这周收集的可回收垃圾被回收后所得金额能否达到150元?
19.(本题8分)如图,测得两幢楼之间的距离为,从楼顶观测点的俯视角为,点的俯视角为.求这两幢楼的高度(精确到)
(参考数据:)
(第19题)
20.(本题10分)已知一次函数的图像经过两点.
(第20题)
(1)求该一次函数的解析式.
(2)如图,点是该一次函数的图像上一点,过作轴的垂线分别交经过点的反比函数图像于点和点,以为边的的顶点在轴上,求出点的坐标.
21.(本题10分)如图,在矩形中,是边上一点,的角平分线交的延长线于点,交于点.
(第21题)
(1)求证.
(2)连结,若时,求的长.
22.(本题12分)阅读材料,完成任务.
知识条目 定义:如图1,抛物线与抛物线的图像只有一个公共点,即方程联立有两个相同的解,则称这两条抛物线紧密衔接于点.
图形应用 在景观设计中,无论是在传统亦或是现代,东方亦或是西方,弧线在各类设计作品中都大量的存在,并被人们赋予了更多丰富的内涵,具有运动的美感。
知识延伸 任务一:在图1中,分别是这两段抛物线的顶点,请证明,且三点共线.
知识应用 如图3,长方形是一处景观,米,米,分别是边的中点,是上的点,设计了两段抛物线和抛物线紧密衔接于点分别是两条抛物线的顶点,点落在边上.分别是的中点,以为圆心,为半径,和以为圆心,的一半长度为半径设计两个圆形花坛.任务二:如图3,当与相切于点时,请建立合适的直角坐标系,求出这两段抛物线的解析式.任务三:为了设计整体感观更加和谐,使三点共线,求出此时上的点到边最小长度.
23.(本题12分)如图,在Rt中,是斜边上一点,以为圆心,以为半径的圆与边相切于点,交于点,是下半圆弧上的中点,连结交于点.已知.
(第23题)
(1)证明:.
(2)求的半径和的长.
(3)是上一点,连结,若直线与四边形的某一边所在的直线垂直,请求出所有满足条件时的的长.
2023学年第二学期九年级入学检测
数学卷参考评分标准
一、选择题(本题有10小题,每小题3分,共30分.每小题只有一个选项是正确的,不选、多选、错选,均不给分)
题号 1 2 3 4 5 6 7 8 9 10
答案 B A B C B C D D A D
二、填空题(本题有6题,每小题4分,共24分)
11. 12. 13. 14. 15.16° 16.10
三、解答题(本题有7小题,共66分,解答需写出必要的文字说明、演算步骤或证明过程)
17.(本题6分)解:
经检验:是原方程的增根,舍去
∴原方程无解.
18.(本题8分)(1)由直方图可知b=3,∴a=30 6 9 3=12.
(2)∵该校这周收集的可回收垃圾的质量小于4.5×6+5×12+5.5×9+6×3=154.5(kg),
∴该校这周收集的可回收垃圾被回收后所得金额小于154.5×0.8=123.6元,
∴该校这周收集的可回收垃圾被回收后所得金额不能达到150元.
19.(本题8分)
过点D作DF⊥AB于F点,
在Rt△ABC中,∠ACB=∠CAE=45°,
∴AB=BC×tan∠ACB=25.4×tan45°=25.4(m).
在Rt△ADF中,∠ADF=∠DAE=35°,DF=BC=25.4(m)
∴AF=DF×tan∠ADF=25.4×tan35°≈25.4×0.70=17.78(m).
∴CD=AB AF=25.4 17.78=7.62≈7.6(m).
20.(本题10分)
解:(1)将A(1,2),B(4, 1)代入得,
,解得,
∴该一次函数的解析式为.
(2)设P(m, m+3),
∵经过A(1,2)的反比例函数解析式为,
经过B(4, 1)的反比例函数解析式为,
∴C(m,),D(m,),
∴CD=.
∵在□ACDE中,AE∥CD,CD⊥x轴,
∴AE⊥x轴,∴AE=CD=2,
∴=2,∴m=3,∴P(3,0)
21.(本题10分)
(1)∵在矩形ABCD中,AD∥BC即AD∥BF,
∴∠DAF=∠F.
∵AF平分∠DAE,
∴∠DAF=∠EAF,
∴∠EAF=∠F,
∴EF=AE.
(2)∵EG⊥AE,∴∠AEG=90°.
∵在矩形ABCD中,∠D=90°,
∴∠AEG=∠D.
∵∠DAF=∠EAF,AG=AG,
∴△AEG≌△ADG,
∴AE=AD=10.
∵在Rt△ABE中,AB=8,
∴BE=.
∵EF=AE=AD=BC,
∴EC+CF=EC+BE,∴CF=BE=6.
22.(本题12分)
任务一:由定义可知有两个相同的解,
即有两个相同的解,
∴,
∴,即.
过M,N分别作x轴的垂线,交x轴于点P,Q,连结OM,ON
∵M,N分别是这两段抛物线的顶点,
∴M(m,),N(n,)
∴MP=,NQ=,OP=,OQ=n
∴tan∠POM=,tan∠QON=
∴tan∠POM=tan∠QON,∴∠POM=∠QON,
∴M,O,N三点共线.
任务二:以G为原点,直线EF为x轴建立直角坐标系,
∴两段抛物线解析式可设为()与()
连结MN,由任务一可知MN经过G点,且
,
∵⊙O2与BC相切,∴NO2=.
∵GF=4NO2=16,∴F(16,0),N(8, 4)代入得,
,,∴.
∵EG=EF GF=24 16=8,∴GO1=,E( 8,0),
∴,∴M( 4,2)
将E( 8,0),M( 4,2)代入得,
,,∴.
任务三:
设,
∵A,M,F三点共线,∴△MFO1∽△AFE,
∴,∴,
∴,
∴.
∵,∴解得或(舍去)
∴,∴⊙O2的半径为,
∴⊙O2上的点到BC边最小长度为(m).
23.(本题12分)
(1)如图,连结OD,OF,
∵⊙O与AC相切于D,
∴OD⊥AC,∴∠ADO=∠ADG+∠ODG=90°.
∵F是下半圆弧上的中点,
∴∠FOG=90°即∠OGF+∠F=90°.
∵OD=OF,∴∠ODG=∠F,
∴∠ADG=∠OGF.
又∵∠OGF=∠DGA,∴∠ADG=∠DGA,
∴AG=AD.
(2)设⊙O的半径为r,
∵OG=1,∴EG=r 1.
∵AE=2,∴AG=r+1,OA=r+2,
∴AD=AG=r+1.
在Rt△ADO中,有勾股定理可知,
,解得,
∴AD=r+1=4,AO=r+2=5,AB=2r+2=8,
∴cos∠A=,,
∴CD=.
(3)①如图1,当M为BC与⊙O相交的点时,则BM⊥AC,
图1
连结EM,
∵BE是直径,
∴∠BME=90°=∠C,
∴EM∥AC,
∴∠MEB=∠A,
∴sin∠A=,∴.
②如图2,设BC与⊙O的交点为N,当MN为直径时,BM⊥BC,
图2
由①可知,
∵MN=2r=6,则BM=.
③如图3,当BM⊥DF时,记垂足为H,连结BD,BF,
∵F是下半圆弧上的中点,
∴=90°,∴∠BDF=45°,
∴∠DBM=45°,
∴=90°=,
∴,即,
∴BM=DF.
∵易得,∴BD=,
∴DH=BH=.
∵BF=,∴HF=,
∴BM=DF=DH+HF=.
综上所述,直线BM与四边形BCDG的某一边所在的直线垂直时,
BM的长度为,或.
数学试卷
亲爱的同学:
欢迎你参加考试!做题时要认真审题,积极思考,细心答题,发挥你的最佳水平.
答卷时,请注意以下几点:
1.全卷满分为120分,考试时间120分钟.
2.全卷由试题卷和答题卷两部分组成,请将答案写在答题卷相应的位置,写在试题卷上无效.
3.书写时字迹要工整,清晰,请勿使用涂改液、修正带、计算器等.祝你成功!
一、选择题(本题有10小题,每小题3分,共30分.每小题只有一个选项是正确的,不选、多选、错选均不给分)
1.如图,数轴上点表示的数绝对值最小的是( )
(第1题)
A. B. C. D.
阅读下列材料,完成第2,3题.
【材料】随着新媒体的发展,更好地推动了全民阅读,一些学者、作家、文化文艺名人等担任“领读人”,通过直播、短视频以及图文等形式,利用新媒体平台助力大众阅读.经典名著依旧是大众推崇的书目,经统计四大名著相关读书视频总播放量已超过3亿,具体数据如图1所示.
图1
2.四大名著中,哪一本名著的相关视频最受欢迎( )
A.《红楼梦》 B.《西游记》 C.《三国演义》 D.《水浒传》
3.四大名著相关读书视频总播放量中,《西游记》的播放量为93000000,请将这个数字用科学记数法表示为( )
A. B. C. D.
4.下列计算正确的是( )
A. B. C. D.
5.剪纸是中国古代最古老的民间艺术之一,其中蕴含着图形的变换.如图是一张蕴含着轴对称变换的蝴蝶剪纸,点与点对称,点与点对称,将其放置在直角坐标系中,点,,的坐标分别为,,,则点的坐标为( )
(第5题)
A. B. C. D.
6.如图,点是的重心,过点作的平行线,分别交,于点,若,则的长为( )
(第6题)
A.2 B.3 C.4 D.5
7.某人买了甲、乙两个品牌的衬衣共件,其中甲品牌衬衣比乙品牌衬衣多5件.已知甲品牌衬衣的单价为120元,乙品牌衬衣的单价为90元,则买这件衬衣共需付款( )
A. B. C. D.
8.一组7个数据分别为,,,,,,.若去掉一个数据,平均数不变,则下列说法正确的是( )
A.中位数与众数都不变 B.众数与方差都不变
C.中位数与极差都不变 D.众数与极差都不变
9.已知二次函数,当时,则( )
A.若时,函数有最小值 B.若时,函数有最小值
C.若时,函数有最小值 D.若时,函数有最小值
10.由四个全等的直角三角形和一个小正方形组成的大正方形如图所示.点是正方形的中心,连结并延长交于点,连结,记的面积为,正方形的面积为.若,则的值为( )
(第10题)
A. B. C. D.
二、填空题(本题有6小题,每小题4分,共24分)
11.计算:______.
12.不等式的解是______.
13.某班45名学生体重达标情况(单位:人)如下表所示,在该班中随机抽取一名学生,其体重为标准的概率是______.
体重 偏瘦 标准 超重 肥胖
人数 3 36 4 2
14.一扇形的圆心角为,弧长为,则该扇形的半径为______.
15.如图,内有一Rt,,,点在圆上,边经过圆心.是平移后的图像,点,的对应点,在上,点的对应点在外,若与相切,连结,则______ .
(第15题)
16.如图1所示的长方形是一种小礼盒的俯视图,其长为4,宽为1.现将若干个小礼盒如图2所示摆放到一个俯视图为正方形的大礼盒中,若留空的部分(阴影部分)的面积是整个正方形面积的,则大正方形边长最小是______.
(第16题)
三、解答题(本题有7小题,共66分,解答应写出文字说明、证明过程或演算步骤)
17.(本题6分)小胡在解分式方程时,发现了问题,请你帮他将正确的解题步骤写出来.
检验:当时,左边.右边左边.
18.(本题8分)某校积极参与垃圾分类活动,以班级为单位收集可回收垃圾.下面是该校30个班级一周收集的可回收垃圾的质量的频数分布表和频数直方图(每组含前一个边界值,不含后一个边界值).
某校30个班级一周收集的可回收垃圾的质量频数表
组别 频数
6
9
某校30个班级一周收集的可回收垃圾的质量频数直方图
(1)求和的值,并补全频数直方图.
(2)已知收集的可回收垃圾以0.8元被回收,该校这周收集的可回收垃圾被回收后所得金额能否达到150元?
19.(本题8分)如图,测得两幢楼之间的距离为,从楼顶观测点的俯视角为,点的俯视角为.求这两幢楼的高度(精确到)
(参考数据:)
(第19题)
20.(本题10分)已知一次函数的图像经过两点.
(第20题)
(1)求该一次函数的解析式.
(2)如图,点是该一次函数的图像上一点,过作轴的垂线分别交经过点的反比函数图像于点和点,以为边的的顶点在轴上,求出点的坐标.
21.(本题10分)如图,在矩形中,是边上一点,的角平分线交的延长线于点,交于点.
(第21题)
(1)求证.
(2)连结,若时,求的长.
22.(本题12分)阅读材料,完成任务.
知识条目 定义:如图1,抛物线与抛物线的图像只有一个公共点,即方程联立有两个相同的解,则称这两条抛物线紧密衔接于点.
图形应用 在景观设计中,无论是在传统亦或是现代,东方亦或是西方,弧线在各类设计作品中都大量的存在,并被人们赋予了更多丰富的内涵,具有运动的美感。
知识延伸 任务一:在图1中,分别是这两段抛物线的顶点,请证明,且三点共线.
知识应用 如图3,长方形是一处景观,米,米,分别是边的中点,是上的点,设计了两段抛物线和抛物线紧密衔接于点分别是两条抛物线的顶点,点落在边上.分别是的中点,以为圆心,为半径,和以为圆心,的一半长度为半径设计两个圆形花坛.任务二:如图3,当与相切于点时,请建立合适的直角坐标系,求出这两段抛物线的解析式.任务三:为了设计整体感观更加和谐,使三点共线,求出此时上的点到边最小长度.
23.(本题12分)如图,在Rt中,是斜边上一点,以为圆心,以为半径的圆与边相切于点,交于点,是下半圆弧上的中点,连结交于点.已知.
(第23题)
(1)证明:.
(2)求的半径和的长.
(3)是上一点,连结,若直线与四边形的某一边所在的直线垂直,请求出所有满足条件时的的长.
2023学年第二学期九年级入学检测
数学卷参考评分标准
一、选择题(本题有10小题,每小题3分,共30分.每小题只有一个选项是正确的,不选、多选、错选,均不给分)
题号 1 2 3 4 5 6 7 8 9 10
答案 B A B C B C D D A D
二、填空题(本题有6题,每小题4分,共24分)
11. 12. 13. 14. 15.16° 16.10
三、解答题(本题有7小题,共66分,解答需写出必要的文字说明、演算步骤或证明过程)
17.(本题6分)解:
经检验:是原方程的增根,舍去
∴原方程无解.
18.(本题8分)(1)由直方图可知b=3,∴a=30 6 9 3=12.
(2)∵该校这周收集的可回收垃圾的质量小于4.5×6+5×12+5.5×9+6×3=154.5(kg),
∴该校这周收集的可回收垃圾被回收后所得金额小于154.5×0.8=123.6元,
∴该校这周收集的可回收垃圾被回收后所得金额不能达到150元.
19.(本题8分)
过点D作DF⊥AB于F点,
在Rt△ABC中,∠ACB=∠CAE=45°,
∴AB=BC×tan∠ACB=25.4×tan45°=25.4(m).
在Rt△ADF中,∠ADF=∠DAE=35°,DF=BC=25.4(m)
∴AF=DF×tan∠ADF=25.4×tan35°≈25.4×0.70=17.78(m).
∴CD=AB AF=25.4 17.78=7.62≈7.6(m).
20.(本题10分)
解:(1)将A(1,2),B(4, 1)代入得,
,解得,
∴该一次函数的解析式为.
(2)设P(m, m+3),
∵经过A(1,2)的反比例函数解析式为,
经过B(4, 1)的反比例函数解析式为,
∴C(m,),D(m,),
∴CD=.
∵在□ACDE中,AE∥CD,CD⊥x轴,
∴AE⊥x轴,∴AE=CD=2,
∴=2,∴m=3,∴P(3,0)
21.(本题10分)
(1)∵在矩形ABCD中,AD∥BC即AD∥BF,
∴∠DAF=∠F.
∵AF平分∠DAE,
∴∠DAF=∠EAF,
∴∠EAF=∠F,
∴EF=AE.
(2)∵EG⊥AE,∴∠AEG=90°.
∵在矩形ABCD中,∠D=90°,
∴∠AEG=∠D.
∵∠DAF=∠EAF,AG=AG,
∴△AEG≌△ADG,
∴AE=AD=10.
∵在Rt△ABE中,AB=8,
∴BE=.
∵EF=AE=AD=BC,
∴EC+CF=EC+BE,∴CF=BE=6.
22.(本题12分)
任务一:由定义可知有两个相同的解,
即有两个相同的解,
∴,
∴,即.
过M,N分别作x轴的垂线,交x轴于点P,Q,连结OM,ON
∵M,N分别是这两段抛物线的顶点,
∴M(m,),N(n,)
∴MP=,NQ=,OP=,OQ=n
∴tan∠POM=,tan∠QON=
∴tan∠POM=tan∠QON,∴∠POM=∠QON,
∴M,O,N三点共线.
任务二:以G为原点,直线EF为x轴建立直角坐标系,
∴两段抛物线解析式可设为()与()
连结MN,由任务一可知MN经过G点,且
,
∵⊙O2与BC相切,∴NO2=.
∵GF=4NO2=16,∴F(16,0),N(8, 4)代入得,
,,∴.
∵EG=EF GF=24 16=8,∴GO1=,E( 8,0),
∴,∴M( 4,2)
将E( 8,0),M( 4,2)代入得,
,,∴.
任务三:
设,
∵A,M,F三点共线,∴△MFO1∽△AFE,
∴,∴,
∴,
∴.
∵,∴解得或(舍去)
∴,∴⊙O2的半径为,
∴⊙O2上的点到BC边最小长度为(m).
23.(本题12分)
(1)如图,连结OD,OF,
∵⊙O与AC相切于D,
∴OD⊥AC,∴∠ADO=∠ADG+∠ODG=90°.
∵F是下半圆弧上的中点,
∴∠FOG=90°即∠OGF+∠F=90°.
∵OD=OF,∴∠ODG=∠F,
∴∠ADG=∠OGF.
又∵∠OGF=∠DGA,∴∠ADG=∠DGA,
∴AG=AD.
(2)设⊙O的半径为r,
∵OG=1,∴EG=r 1.
∵AE=2,∴AG=r+1,OA=r+2,
∴AD=AG=r+1.
在Rt△ADO中,有勾股定理可知,
,解得,
∴AD=r+1=4,AO=r+2=5,AB=2r+2=8,
∴cos∠A=,,
∴CD=.
(3)①如图1,当M为BC与⊙O相交的点时,则BM⊥AC,
图1
连结EM,
∵BE是直径,
∴∠BME=90°=∠C,
∴EM∥AC,
∴∠MEB=∠A,
∴sin∠A=,∴.
②如图2,设BC与⊙O的交点为N,当MN为直径时,BM⊥BC,
图2
由①可知,
∵MN=2r=6,则BM=.
③如图3,当BM⊥DF时,记垂足为H,连结BD,BF,
∵F是下半圆弧上的中点,
∴=90°,∴∠BDF=45°,
∴∠DBM=45°,
∴=90°=,
∴,即,
∴BM=DF.
∵易得,∴BD=,
∴DH=BH=.
∵BF=,∴HF=,
∴BM=DF=DH+HF=.
综上所述,直线BM与四边形BCDG的某一边所在的直线垂直时,
BM的长度为,或.
同课章节目录
