第二十六章 反比例函数 达标检测卷 (含解析)人教版九年级数学下册
文档属性
| 名称 | 第二十六章 反比例函数 达标检测卷 (含解析)人教版九年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 267.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-21 21:37:13 | ||
图片预览



文档简介
第二十六章 反比例函数 达标检测卷 人教版九年级化学下册
一、选择题
1.下列函数是y关于x的反比例函数的是( )
A.y= B.y= C.y=﹣ D.y=﹣
2.反比例函数的图象一定经过的点是( )
A. B. C. D.
3.已知y与x成正比例,z与y成反比例,则z与x之间的关系为( )
A.成正比例 B.成反比例
C.既成正比例又成反比例 D.既不成正比例又不成反比例
4.反比例函数y= (x<0)的图象位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.如图,的直角顶点在坐标原点上,点在反比例函数的图象上,点在反比例函数的图象上,则的值是( )
A. B. C. D.
6.在反比例函数图象的每一支上,y都随x的增大而增大.则k的取值范围是( )
A. B. C. D.
7.如图,在直角坐标系xOy中,点A,B分别在x轴和y轴,.∠AOB的角平分线与OA的垂直平分线交于点C,与AB交于点D,反比例函数y=的图象过点C.当以CD为边的正方形的面积为时,k的值是( )
A.2 B.3 C.5 D.7
8. 某综合实践活动小组设计了简易电子体重秤: 制作一个装有踏板(踏板质量忽略不计)的可变电阻 (如图 1), 当人站上踏板时, 通过电压表显示的读数 换算为人的质量 ), 已知 随着 的变化而变化 (如图 2), 与踏板上人的质量 的关系见图3. 则下列说法不正确的是 ( )
A.在一定范围内, 越大, 越小
B.当 时, 的阻值为
C.当踏板上人的质量为 时,
D.若电压表量程为 , 为保护电压表, 该电子体重科可称的最大质量是
二、填空题
9.若函数是反比例函数,则的值等于 .
10.函数y= 的自变量x的取值范围是 。
11.如图,将一把矩形直尺和一块含角的三角板摆放在平面直角坐标系中,在轴上,点与点重合,点在上,三角板的直角边交于点,反比例函数的图象恰好经过点,若直尺的宽,三角板的斜边,则 .
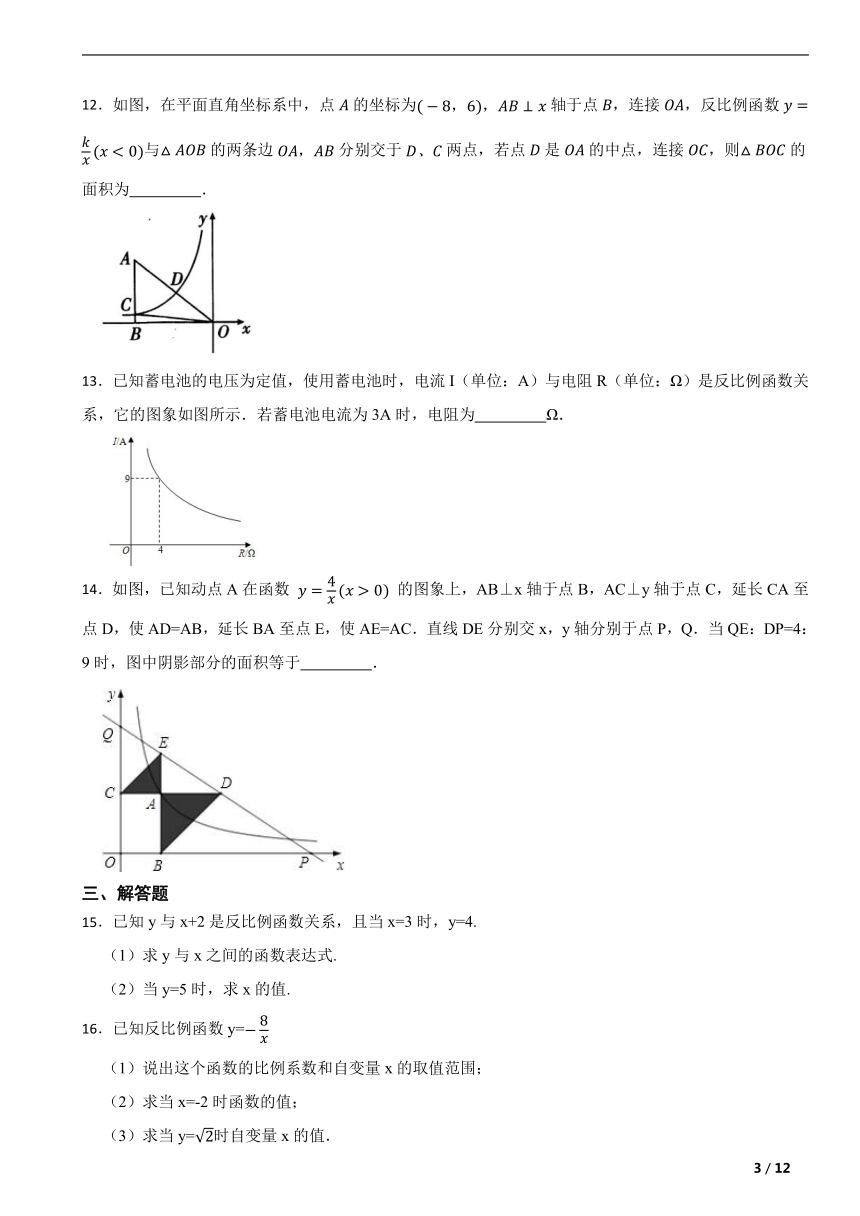
12.如图,在平面直角坐标系中,点的坐标为轴于点,连接,反比例函数与的两条边分别交于两点,若点是的中点,连接,则的面积为 .
13.已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示.若蓄电池电流为3A时,电阻为 Ω.
14.如图,已知动点A在函数 的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA至点D,使AD=AB,延长BA至点E,使AE=AC.直线DE分别交x,y轴分别于点P,Q.当QE:DP=4:9时,图中阴影部分的面积等于 .
三、解答题
15.已知y与x+2是反比例函数关系,且当x=3时,y=4.
(1)求y与x之间的函数表达式.
(2)当y=5时,求x的值.
16.已知反比例函数y=
(1)说出这个函数的比例系数和自变量x的取值范围;
(2)求当x=-2时函数的值;
(3)求当y=时自变量x的值.
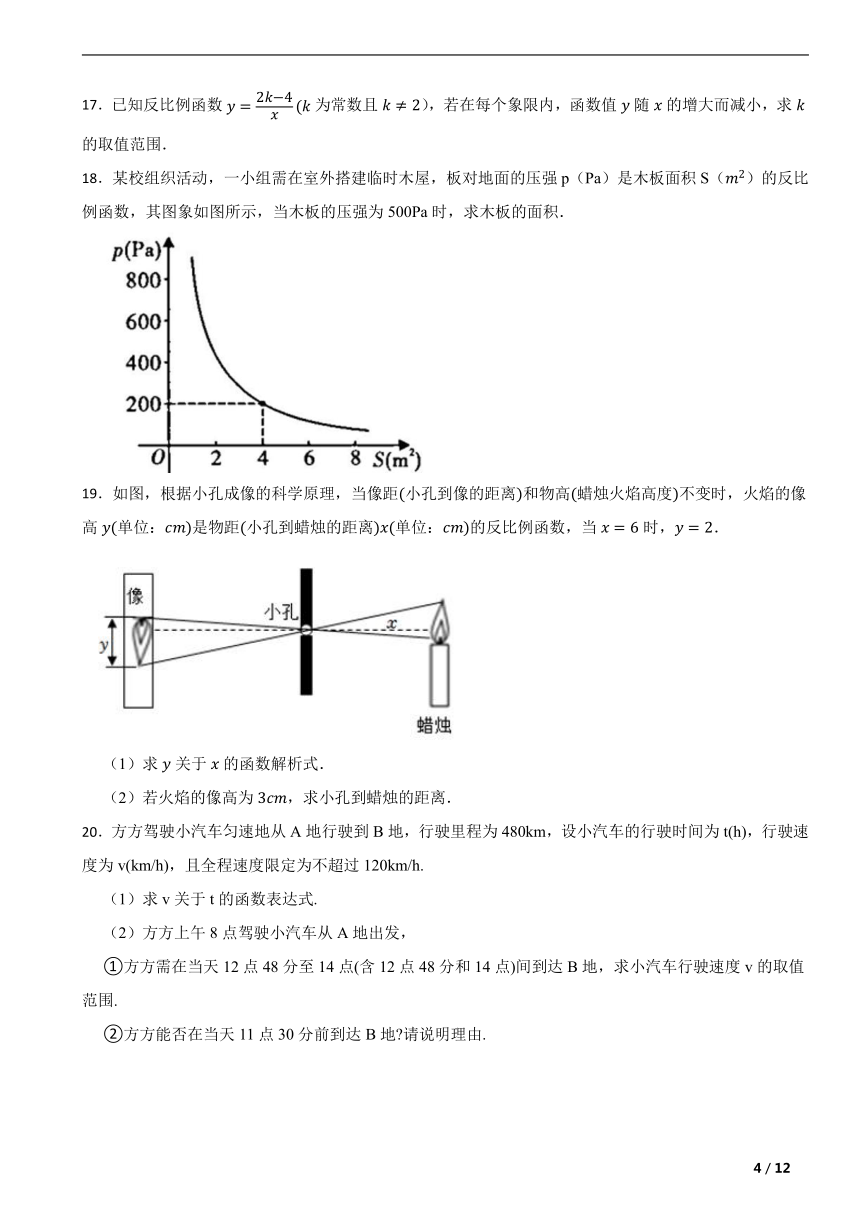
17.已知反比例函数为常数且),若在每个象限内,函数值随的增大而减小,求的取值范围.
18.某校组织活动,一小组需在室外搭建临时木屋,板对地面的压强p(Pa)是木板面积S()的反比例函数,其图象如图所示,当木板的压强为500Pa时,求木板的面积.
19.如图,根据小孔成像的科学原理,当像距小孔到像的距离和物高蜡烛火焰高度不变时,火焰的像高单位:是物距小孔到蜡烛的距离单位:的反比例函数,当时,.
(1)求关于的函数解析式.
(2)若火焰的像高为,求小孔到蜡烛的距离.
20.方方驾驶小汽车匀速地从A地行驶到B地,行驶里程为480km,设小汽车的行驶时间为t(h),行驶速度为v(km/h),且全程速度限定为不超过120km/h.
(1)求v关于t的函数表达式.
(2)方方上午8点驾驶小汽车从A地出发,
①方方需在当天12点48分至14点(含12点48分和14点)间到达B地,求小汽车行驶速度v的取值范围.
②方方能否在当天11点30分前到达B地 请说明理由.
答案解析部分
1.【答案】C
2.【答案】C
【解析】【解答】解:∵k=-4,
∴在反比例函数图像上的点横纵坐标相乘等于-4,
∴1×4=(-1)×(-4)=2×2=4,(-2)×2=-4,
∴在函数图象上,
故答案为:C
【分析】根据反比例函数k的性质,结合题意对选项逐一计算即可求解。
3.【答案】B
【解析】【解答】解:y与x成正比例 ,可设,
z与y成反比例,可设,
把代入中,得,
k、a都不等于0,是z关于x 的反比例函数,
z与x之间的关系为成反比例.
故答案为:B.
【分析】根据y与x成正比例,z与y成反比例可设、,把代入中即可得到z与x之间的关系.
4.【答案】C
【解析】【解答】解:∵反比例函数y= (x<0)中,k=1>0,
∴该函数图象在第三象限,
故答案为:C.
【分析】根据反比例函数的图象与系数的关系和x的取值范围,可以解答本题.
5.【答案】B
【解析】【解答】解:如图,过点B作BC⊥x轴于点C,过点A作AD⊥x轴于点D,
∴∠BCO=∠ADO=90°,
∵点A、B分别在反比例函数与的图象上 ,
∴S△ADO=×4=2,S△BCO=×1=,
∴,
∵∠AOB=90°,
∴∠BOC+∠AOD=∠BOC+∠OBC=90°,
∴∠AOD=∠OBC,
∴△BOC∽△OAD
,∴,
∴,
∴tan∠BAO=.
故答案为:B.
【分析】过点B作BC⊥x轴于点C,过点A作AD⊥x轴于点D,根据反比例函数k的几何意义可得S△ADO=×4=2,S△BCO=×1=,进而可得,然后由有两组角对应相等得两个三角形相似得△BOC∽△OAD,由相似三角形面积的比等于相似比的平方可得,最后根据正切函数的定义即可求出tan∠BAO的正切值.
6.【答案】B
【解析】【解答】解:在反比例函数图象的每一支上,y都随x的增大而增大.
,
,
故答案为:B.
【分析】根据反比例函数的性质结合题意可得k-2<0,求解可得k的范围.
7.【答案】D
【解析】【解答】设OA=3a,则OB=4a,设直线AB的解析式是y=kx+b,则根据题意得:,解得:,则直线AB的解析式是y=﹣x+4a,
直线CD是∠AOB的平分线,则OD的解析式是y=x.根据题意得:,解得:则D的坐标是(,),
OA的中垂线的解析式是x=,则C的坐标是(,),则k=.∵以CD为边的正方形的面积为,∴2(﹣)2=,则a2=,
∴k=×=7.故选D.
【分析】设OA=3a,则OB=4a,利用待定系数法即可求得直线AB的解析式,直线CD的解析式是y=x,OA的中垂线的解析式是x=,解方程组即可求得C和D的坐标,根据以CD为边的正方形的面积为,即CD2=,据此即可列方程求得a2的值,则k即可求解.
8.【答案】C
【解析】【解答】解:A、图2中的图象可知, 在一定范围内, 越大, 越小,故A不符合题意;
B、由图2可知,图象经过点(50,3),
当U0=3V时,R1的阻值为50Ω,故B不符合题意;
C、当m=90kg时,R1=-2m+240=60Ω,
∴当U0=2V时,对应的是90Ω,
∴当踏板上人的质量为90kg时,U0=2V错误,故C符合题意;
D、∵R1=-2m+240,
∴R1随m的增大而减小,
∴R1的最小值为10,
∴-2m+240=10,
解之:m=115,
∴m的最大值为115kg,
∴ 若电压表量程为 , 为保护电压表, 该电子体重科可称的最大质量是 ,故D不符合题意;
故答案为:C.
【分析】利用图2,可对A,B作出判断;将m=90代入R1=-2m+240,可求出R1的值,由此可得当U0=2V时,对应的是90Ω,可对C作出判断;由R1=-2m+240,利用一次函数的性质可知R1随m的增大而减小,可得到R1的最小值为10,可求出m的最大值,可对D作出判断.
9.【答案】
【解析】【解答】解:∵函数是反比例函数,
∴m2-2=-1,且m-1≠0,
解得:m=-1.
故答案为:-1.
【分析】根据反比例函数的定义,可得m2-2=-1,且m-1≠0,解得m=-1.
10.【答案】x≠1
【解析】【解答】解:∵,
∴x-1≠0,
解得:x≠1.
故答案为:x≠1.
【分析】因为此函数是反比例函数,解析式为分式,根据分式有意义的条件,分母不为0,列出不等式,解不等式即可.
11.【答案】
【解析】【解答】解:过点M作,垂足为N,则四边形CDNM为矩形,故MN=CD=2,又∵在中,则又∵,∴设点A的坐标为,则点B的坐标为,故点F、M的坐标分别为:又 反比例函数的图象恰好经过点,∴解得则.
故答案为:.
【分析】本题主要考查反比函数的基本性质、含30°直角三角形的性质,过点M作,垂足为N,根据题意可得:MN=CD=2,然后通过解直角三角形可得:进而得到:设点A的坐标为,则点B的坐标为,故点F、M的坐标分别为:然后带入反比例函数解析式建立方程求解即可.
12.【答案】6
13.【答案】12
【解析】【解答】解:设该反比函数解析式为 ,
根据题意得:当 时, ,
∴ ,解得: ,
∴该反比函数解析式为,
∴当 时, ,
即电阻为12Ω.
故答案为:12
【分析】设该反比函数解析式为 ,先求出反比例函数解析式,再将代入反比例函数解析式求解即可。
14.【答案】
【解析】【解答】解:
解法一:过点D作DG⊥x轴于点G,过点E作EF⊥y轴于点F.
令A(t, ),则AD=AB=DG= ,AE=AC=EF=t.
在直角△ADE中,由勾股定理,得DE= = = = .
∵△EFQ∽△DAE,
∴QE:DE=EF:AD,
∴QE= ,
∵△ADE∽△GPD,
∴DE:PD=AE:DG,
∴DP= .
又∵QE:DP=4:9,
∴ : =4:9,
解得t2= .
∴图中阴影部分的面积= AC2+ AB2= t2+ × = +3= ;
解法二:∵QE:DP=4:9,
∴EF:PG=4:9,
设EF=4t,则PG=9t,
∴A(4t, ),
由AC=AE AD=AB,
∴AE=4t,AD= ,DG= ,GP=9t,
∵△ADE∽△GPD,
∴AE:DG=AD:GP,
4t: = :9t,即t2= ,
图中阴影部分的面积= ×4t×4t+ × × = .
故答案为: .
【分析】过点D作DG⊥x轴于点G,过点E作EF⊥y轴于点F.令A(t, ),则AD=AB=DG= ,AE=AC=EF=t,则图中阴影部分的面积=△ACE的面积+△ABD的面积= t2+ × ,因此只需求出t2的值即可.先在直角△ADE中,由勾股定理,得出DE= ,再由△EFQ∽△DAE,求出QE= ,△ADE∽△GPD,求出DP=: ,然后根据QE:DP=4:9,即可得出t2= .
15.【答案】(1)解:∵ y与x+2是反比例函数关系,
∴设y=,
∵ 当x=3时,y=4,
∴4=,解得K=20,
故y与x之间的函数表达式为:;
(2)解:由题意,把y=5代入(1)中的解析式:
,解得:x=2.
【解析】【分析】(1)设y=,由题意把x=3,y=4代入解析式可得关于k的方程,解方程可求解;
(2)由题意把y=5代入(1)中的解析式可得关于x的方程,解方程即可求解.
16.【答案】(1)∵y=,∴该函数的比例系数是-8;
自变量x的取值范围是x≠0.
(2)当x=-2时,y==4.
(3)当y=时,可得=,解得x=.
【解析】【分析】(1)根据反比例函数中的比例系数和分母为0无意义,即可求解.
(2)把x=-2代入 y= 中计算即可.
(3)把 y= 代入 y=解方程即可得到x的值.
17.【答案】解:反比例函数在每个象限内,函数值随的增大而减小,
,
解得,
的取值范围是.
18.【答案】解:设木板对地面的压强与木板面积之间的函数表达式为,
将代入,得,
解得,
从板对地面的压强与从板面积之间的函数表达式为,
当时,有,解得,
当木板的压强为时,木板的面积为.
19.【答案】(1)解:由题意设:,
把,代入,得,
关于的函数解析式为:;
(2)解:把代入,得,,
小孔到蜡烛的距离为.
【解析】【分析】(1)利用待定系数法求函数解析式即可;
(2)将y=3代入函数解析式计算求解即可。
20.【答案】(1)解:∵vt=480,
∴.
(2)解:① 8点至12点48分时间长为小时, 8点至14点时间长为6小时,
把t=6代入得v=80,
把t=代入得v=100,
∴ 小汽车行驶速度v的取值范围80≤v≤100.
②不能.
理由:8点至11点30分时间长为小时,
把t=代入得v=>120,
∴方方能否在当天11点30分前到达B地 .
【解析】【分析】(1)根据路程=速度×时间进行列式,再变形即可;
(2)①8点至12点48分时间长为小时, 8点至14点时间长为6小时,把t值分别代入中求出v值,继而得解;
②8点至11点30分时间长为小时,将t值代入求出v值再与120km/h比较即可判断.
1 / 1
一、选择题
1.下列函数是y关于x的反比例函数的是( )
A.y= B.y= C.y=﹣ D.y=﹣
2.反比例函数的图象一定经过的点是( )
A. B. C. D.
3.已知y与x成正比例,z与y成反比例,则z与x之间的关系为( )
A.成正比例 B.成反比例
C.既成正比例又成反比例 D.既不成正比例又不成反比例
4.反比例函数y= (x<0)的图象位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.如图,的直角顶点在坐标原点上,点在反比例函数的图象上,点在反比例函数的图象上,则的值是( )
A. B. C. D.
6.在反比例函数图象的每一支上,y都随x的增大而增大.则k的取值范围是( )
A. B. C. D.
7.如图,在直角坐标系xOy中,点A,B分别在x轴和y轴,.∠AOB的角平分线与OA的垂直平分线交于点C,与AB交于点D,反比例函数y=的图象过点C.当以CD为边的正方形的面积为时,k的值是( )
A.2 B.3 C.5 D.7
8. 某综合实践活动小组设计了简易电子体重秤: 制作一个装有踏板(踏板质量忽略不计)的可变电阻 (如图 1), 当人站上踏板时, 通过电压表显示的读数 换算为人的质量 ), 已知 随着 的变化而变化 (如图 2), 与踏板上人的质量 的关系见图3. 则下列说法不正确的是 ( )
A.在一定范围内, 越大, 越小
B.当 时, 的阻值为
C.当踏板上人的质量为 时,
D.若电压表量程为 , 为保护电压表, 该电子体重科可称的最大质量是
二、填空题
9.若函数是反比例函数,则的值等于 .
10.函数y= 的自变量x的取值范围是 。
11.如图,将一把矩形直尺和一块含角的三角板摆放在平面直角坐标系中,在轴上,点与点重合,点在上,三角板的直角边交于点,反比例函数的图象恰好经过点,若直尺的宽,三角板的斜边,则 .
12.如图,在平面直角坐标系中,点的坐标为轴于点,连接,反比例函数与的两条边分别交于两点,若点是的中点,连接,则的面积为 .
13.已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示.若蓄电池电流为3A时,电阻为 Ω.
14.如图,已知动点A在函数 的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA至点D,使AD=AB,延长BA至点E,使AE=AC.直线DE分别交x,y轴分别于点P,Q.当QE:DP=4:9时,图中阴影部分的面积等于 .
三、解答题
15.已知y与x+2是反比例函数关系,且当x=3时,y=4.
(1)求y与x之间的函数表达式.
(2)当y=5时,求x的值.
16.已知反比例函数y=
(1)说出这个函数的比例系数和自变量x的取值范围;
(2)求当x=-2时函数的值;
(3)求当y=时自变量x的值.
17.已知反比例函数为常数且),若在每个象限内,函数值随的增大而减小,求的取值范围.
18.某校组织活动,一小组需在室外搭建临时木屋,板对地面的压强p(Pa)是木板面积S()的反比例函数,其图象如图所示,当木板的压强为500Pa时,求木板的面积.
19.如图,根据小孔成像的科学原理,当像距小孔到像的距离和物高蜡烛火焰高度不变时,火焰的像高单位:是物距小孔到蜡烛的距离单位:的反比例函数,当时,.
(1)求关于的函数解析式.
(2)若火焰的像高为,求小孔到蜡烛的距离.
20.方方驾驶小汽车匀速地从A地行驶到B地,行驶里程为480km,设小汽车的行驶时间为t(h),行驶速度为v(km/h),且全程速度限定为不超过120km/h.
(1)求v关于t的函数表达式.
(2)方方上午8点驾驶小汽车从A地出发,
①方方需在当天12点48分至14点(含12点48分和14点)间到达B地,求小汽车行驶速度v的取值范围.
②方方能否在当天11点30分前到达B地 请说明理由.
答案解析部分
1.【答案】C
2.【答案】C
【解析】【解答】解:∵k=-4,
∴在反比例函数图像上的点横纵坐标相乘等于-4,
∴1×4=(-1)×(-4)=2×2=4,(-2)×2=-4,
∴在函数图象上,
故答案为:C
【分析】根据反比例函数k的性质,结合题意对选项逐一计算即可求解。
3.【答案】B
【解析】【解答】解:y与x成正比例 ,可设,
z与y成反比例,可设,
把代入中,得,
k、a都不等于0,是z关于x 的反比例函数,
z与x之间的关系为成反比例.
故答案为:B.
【分析】根据y与x成正比例,z与y成反比例可设、,把代入中即可得到z与x之间的关系.
4.【答案】C
【解析】【解答】解:∵反比例函数y= (x<0)中,k=1>0,
∴该函数图象在第三象限,
故答案为:C.
【分析】根据反比例函数的图象与系数的关系和x的取值范围,可以解答本题.
5.【答案】B
【解析】【解答】解:如图,过点B作BC⊥x轴于点C,过点A作AD⊥x轴于点D,
∴∠BCO=∠ADO=90°,
∵点A、B分别在反比例函数与的图象上 ,
∴S△ADO=×4=2,S△BCO=×1=,
∴,
∵∠AOB=90°,
∴∠BOC+∠AOD=∠BOC+∠OBC=90°,
∴∠AOD=∠OBC,
∴△BOC∽△OAD
,∴,
∴,
∴tan∠BAO=.
故答案为:B.
【分析】过点B作BC⊥x轴于点C,过点A作AD⊥x轴于点D,根据反比例函数k的几何意义可得S△ADO=×4=2,S△BCO=×1=,进而可得,然后由有两组角对应相等得两个三角形相似得△BOC∽△OAD,由相似三角形面积的比等于相似比的平方可得,最后根据正切函数的定义即可求出tan∠BAO的正切值.
6.【答案】B
【解析】【解答】解:在反比例函数图象的每一支上,y都随x的增大而增大.
,
,
故答案为:B.
【分析】根据反比例函数的性质结合题意可得k-2<0,求解可得k的范围.
7.【答案】D
【解析】【解答】设OA=3a,则OB=4a,设直线AB的解析式是y=kx+b,则根据题意得:,解得:,则直线AB的解析式是y=﹣x+4a,
直线CD是∠AOB的平分线,则OD的解析式是y=x.根据题意得:,解得:则D的坐标是(,),
OA的中垂线的解析式是x=,则C的坐标是(,),则k=.∵以CD为边的正方形的面积为,∴2(﹣)2=,则a2=,
∴k=×=7.故选D.
【分析】设OA=3a,则OB=4a,利用待定系数法即可求得直线AB的解析式,直线CD的解析式是y=x,OA的中垂线的解析式是x=,解方程组即可求得C和D的坐标,根据以CD为边的正方形的面积为,即CD2=,据此即可列方程求得a2的值,则k即可求解.
8.【答案】C
【解析】【解答】解:A、图2中的图象可知, 在一定范围内, 越大, 越小,故A不符合题意;
B、由图2可知,图象经过点(50,3),
当U0=3V时,R1的阻值为50Ω,故B不符合题意;
C、当m=90kg时,R1=-2m+240=60Ω,
∴当U0=2V时,对应的是90Ω,
∴当踏板上人的质量为90kg时,U0=2V错误,故C符合题意;
D、∵R1=-2m+240,
∴R1随m的增大而减小,
∴R1的最小值为10,
∴-2m+240=10,
解之:m=115,
∴m的最大值为115kg,
∴ 若电压表量程为 , 为保护电压表, 该电子体重科可称的最大质量是 ,故D不符合题意;
故答案为:C.
【分析】利用图2,可对A,B作出判断;将m=90代入R1=-2m+240,可求出R1的值,由此可得当U0=2V时,对应的是90Ω,可对C作出判断;由R1=-2m+240,利用一次函数的性质可知R1随m的增大而减小,可得到R1的最小值为10,可求出m的最大值,可对D作出判断.
9.【答案】
【解析】【解答】解:∵函数是反比例函数,
∴m2-2=-1,且m-1≠0,
解得:m=-1.
故答案为:-1.
【分析】根据反比例函数的定义,可得m2-2=-1,且m-1≠0,解得m=-1.
10.【答案】x≠1
【解析】【解答】解:∵,
∴x-1≠0,
解得:x≠1.
故答案为:x≠1.
【分析】因为此函数是反比例函数,解析式为分式,根据分式有意义的条件,分母不为0,列出不等式,解不等式即可.
11.【答案】
【解析】【解答】解:过点M作,垂足为N,则四边形CDNM为矩形,故MN=CD=2,又∵在中,则又∵,∴设点A的坐标为,则点B的坐标为,故点F、M的坐标分别为:又 反比例函数的图象恰好经过点,∴解得则.
故答案为:.
【分析】本题主要考查反比函数的基本性质、含30°直角三角形的性质,过点M作,垂足为N,根据题意可得:MN=CD=2,然后通过解直角三角形可得:进而得到:设点A的坐标为,则点B的坐标为,故点F、M的坐标分别为:然后带入反比例函数解析式建立方程求解即可.
12.【答案】6
13.【答案】12
【解析】【解答】解:设该反比函数解析式为 ,
根据题意得:当 时, ,
∴ ,解得: ,
∴该反比函数解析式为,
∴当 时, ,
即电阻为12Ω.
故答案为:12
【分析】设该反比函数解析式为 ,先求出反比例函数解析式,再将代入反比例函数解析式求解即可。
14.【答案】
【解析】【解答】解:
解法一:过点D作DG⊥x轴于点G,过点E作EF⊥y轴于点F.
令A(t, ),则AD=AB=DG= ,AE=AC=EF=t.
在直角△ADE中,由勾股定理,得DE= = = = .
∵△EFQ∽△DAE,
∴QE:DE=EF:AD,
∴QE= ,
∵△ADE∽△GPD,
∴DE:PD=AE:DG,
∴DP= .
又∵QE:DP=4:9,
∴ : =4:9,
解得t2= .
∴图中阴影部分的面积= AC2+ AB2= t2+ × = +3= ;
解法二:∵QE:DP=4:9,
∴EF:PG=4:9,
设EF=4t,则PG=9t,
∴A(4t, ),
由AC=AE AD=AB,
∴AE=4t,AD= ,DG= ,GP=9t,
∵△ADE∽△GPD,
∴AE:DG=AD:GP,
4t: = :9t,即t2= ,
图中阴影部分的面积= ×4t×4t+ × × = .
故答案为: .
【分析】过点D作DG⊥x轴于点G,过点E作EF⊥y轴于点F.令A(t, ),则AD=AB=DG= ,AE=AC=EF=t,则图中阴影部分的面积=△ACE的面积+△ABD的面积= t2+ × ,因此只需求出t2的值即可.先在直角△ADE中,由勾股定理,得出DE= ,再由△EFQ∽△DAE,求出QE= ,△ADE∽△GPD,求出DP=: ,然后根据QE:DP=4:9,即可得出t2= .
15.【答案】(1)解:∵ y与x+2是反比例函数关系,
∴设y=,
∵ 当x=3时,y=4,
∴4=,解得K=20,
故y与x之间的函数表达式为:;
(2)解:由题意,把y=5代入(1)中的解析式:
,解得:x=2.
【解析】【分析】(1)设y=,由题意把x=3,y=4代入解析式可得关于k的方程,解方程可求解;
(2)由题意把y=5代入(1)中的解析式可得关于x的方程,解方程即可求解.
16.【答案】(1)∵y=,∴该函数的比例系数是-8;
自变量x的取值范围是x≠0.
(2)当x=-2时,y==4.
(3)当y=时,可得=,解得x=.
【解析】【分析】(1)根据反比例函数中的比例系数和分母为0无意义,即可求解.
(2)把x=-2代入 y= 中计算即可.
(3)把 y= 代入 y=解方程即可得到x的值.
17.【答案】解:反比例函数在每个象限内,函数值随的增大而减小,
,
解得,
的取值范围是.
18.【答案】解:设木板对地面的压强与木板面积之间的函数表达式为,
将代入,得,
解得,
从板对地面的压强与从板面积之间的函数表达式为,
当时,有,解得,
当木板的压强为时,木板的面积为.
19.【答案】(1)解:由题意设:,
把,代入,得,
关于的函数解析式为:;
(2)解:把代入,得,,
小孔到蜡烛的距离为.
【解析】【分析】(1)利用待定系数法求函数解析式即可;
(2)将y=3代入函数解析式计算求解即可。
20.【答案】(1)解:∵vt=480,
∴.
(2)解:① 8点至12点48分时间长为小时, 8点至14点时间长为6小时,
把t=6代入得v=80,
把t=代入得v=100,
∴ 小汽车行驶速度v的取值范围80≤v≤100.
②不能.
理由:8点至11点30分时间长为小时,
把t=代入得v=>120,
∴方方能否在当天11点30分前到达B地 .
【解析】【分析】(1)根据路程=速度×时间进行列式,再变形即可;
(2)①8点至12点48分时间长为小时, 8点至14点时间长为6小时,把t值分别代入中求出v值,继而得解;
②8点至11点30分时间长为小时,将t值代入求出v值再与120km/h比较即可判断.
1 / 1
