第二十八章 锐角三角函数 达标检测卷 (含解析)人教版九年级数学下册
文档属性
| 名称 | 第二十八章 锐角三角函数 达标检测卷 (含解析)人教版九年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 420.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-21 21:38:45 | ||
图片预览



文档简介
第二十八章 锐角三角函数 达标检测卷 人教版九年级数学学下册
一、选择题
1.如图,是周长为36的等腰三角形,,,则的值为(
A. B. C. D.
2. 如图,△ABC的三个顶点都在方格纸的格点上,则cosA的值是( )
A. B. C. D.
3.锐角满足,且,则的取值范围为( )
A. B.
C. D.
4.在Rt△ABC中,∠C=90°,若tanA= ,则sinA=( )
A. B. C. D.
5. 在中,,,则的值为( )
A. B. C. D.
6.下列各式中不正确的是( ).
A. B.
C. D.
7. 在△ABC中,tan A=,cos B=,则∠C的度数是( )
A.30° B.45° C.60° D.90°
8. 如图所示,在Rt△ABC中,∠C=90°,D为BC边上一点,∠DAC=30°,BD=2,AB=2,则AC的长是( )
A. B.2 C.3 D.
9.如图1是第七届国际数学教育大会(ICME)会徽,选择其中两个相邻的直角三角形,恰好能组合得到如图2所示的四边形OABC.若AB=BC,sin∠AOB=,则tanC的值为( )
A. B. C. D.
10.由小正方形组成的网格如图,A,B,C三点都在格点上,则∠ABC的正切值为( )
A. B. C. D.
二、填空题
11. 已知为锐角,且,则 °.
12. 在△ABC中,若|2sin A-|与(-2cos B)2互为相反数,则∠C= .
13. 如图所示,已知△ABC的外接圆☉O的半径为3,AC=4,则sin B= .
14. 如图正方形的边长为3,E是上一点且,F是线段上的动点.连接,将线段绕点C逆时针旋转 90°得到,连接,则的最小值是 .
15. 如图所示,测量船以20 n mile/h的速度沿正东方向航行并对某海岛进行测量,测量船在A处测得海岛上观测点D位于北偏东15°方向上,观测点C位于北偏东45°方向上,航行半个小时到达B点,这时测得海岛上观测点C位于北偏西45°方向上,若CD与AB平行,则CD= n mile(计算结果不取近似值).
三、解答题
16.
(1)计算:2sin30°+cos30°·tan60°.
(2)已知,且a+b=20,求a,b的值.
17.已知:等腰三角形ABC中,AB=AC,∠A是锐角,且tanA=.
(1)求sinA;
(2)若BC=,求AB的长.
18. 如图所示,AB是☉O的直径,点E是劣弧BD上一点,∠PAD=∠AED,且DE=,AE平分∠BAD,AE与BD交于点F.
(1)求证:PA是☉O的切线;
(2)若tan∠DAE=,求EF的长.
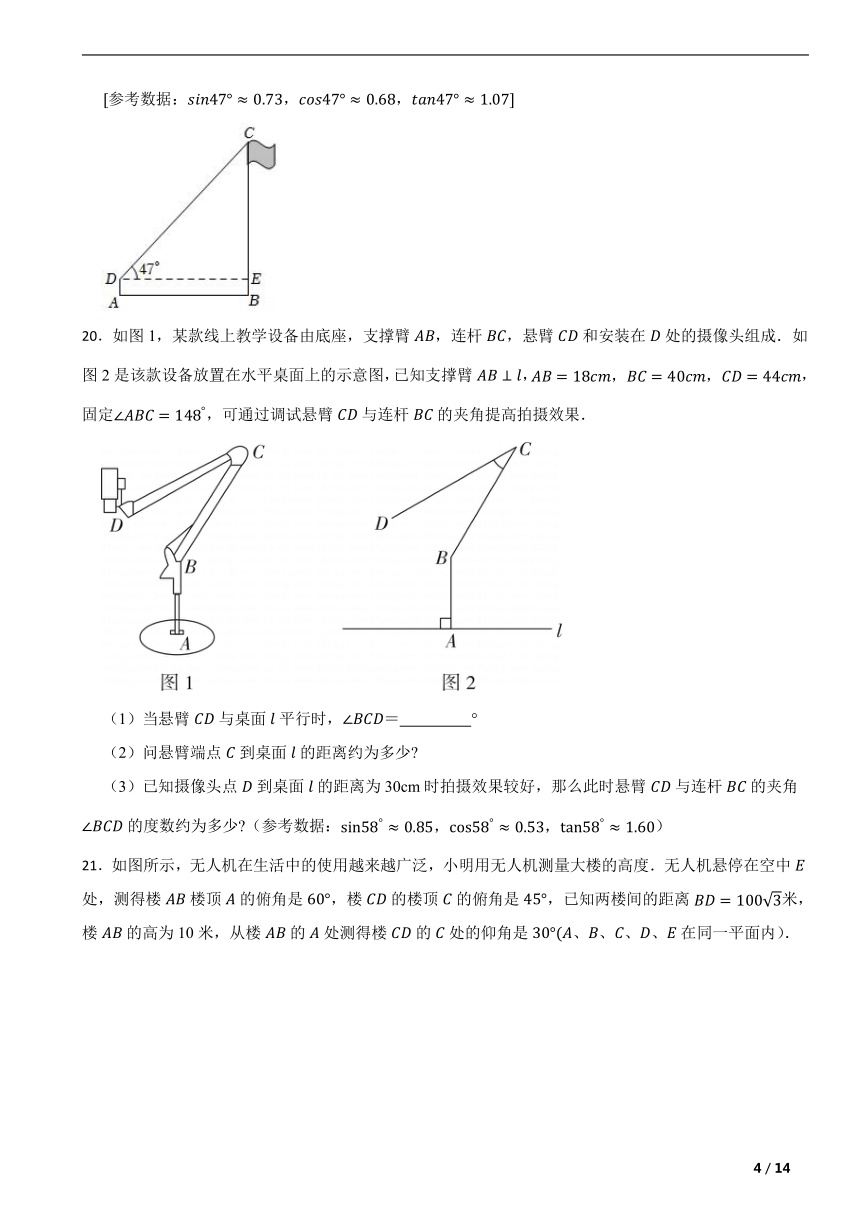
19.如图,为了测量旗杆的高度,在离旗杆底部米的处,用高米的测角仪测得旗杆顶端处的仰角为求旗杆的高.精确到米
参考数据:,,
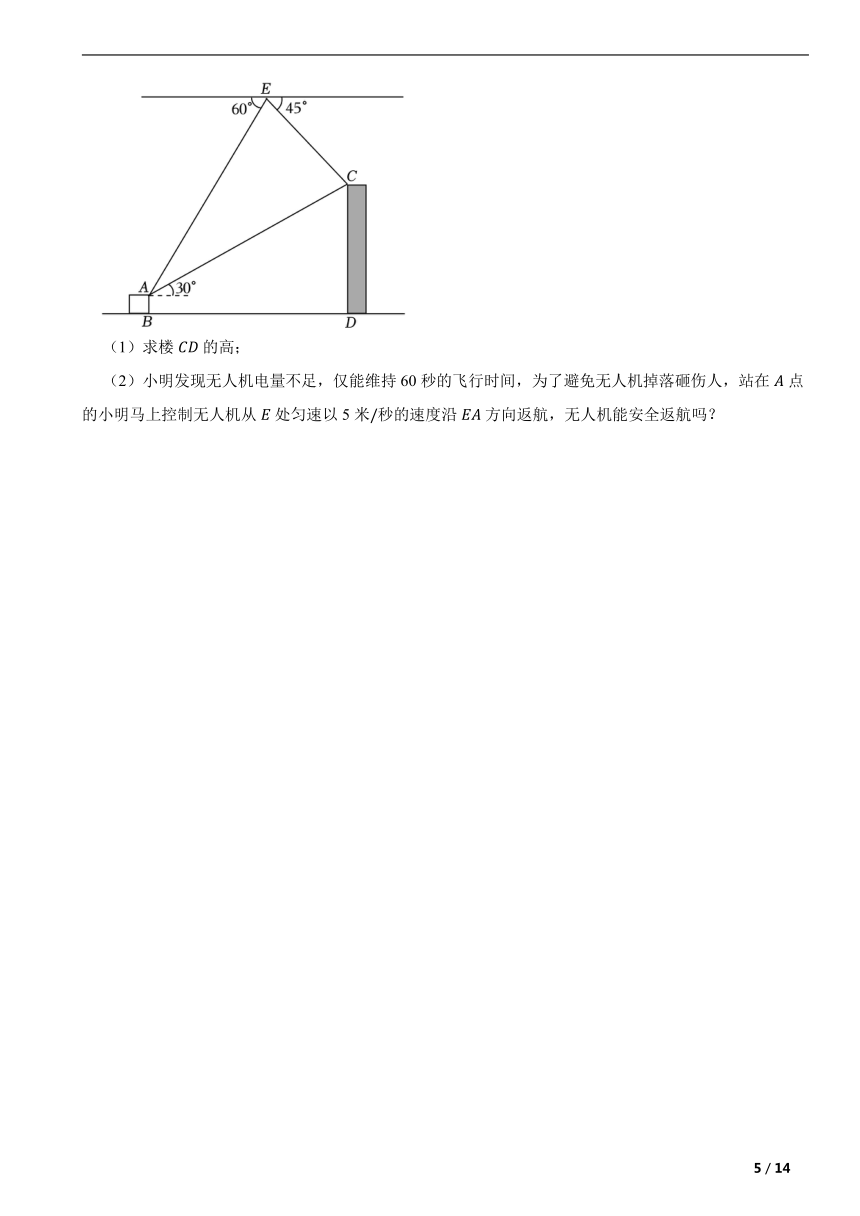
20.如图1,某款线上教学设备由底座,支撑臂,连杆,悬臂和安装在处的摄像头组成.如图2是该款设备放置在水平桌面上的示意图,已知支撑臂,,固定,可通过调试悬臂与连杆的夹角提高拍摄效果.
(1)当悬臂与桌面平行时,= °
(2)问悬臂端点到桌面的距离约为多少
(3)已知摄像头点到桌面的距离为30cm时拍摄效果较好,那么此时悬臂与连杆的夹角的度数约为多少 (参考数据:)
21.如图所示,无人机在生活中的使用越来越广泛,小明用无人机测量大楼的高度.无人机悬停在空中处,测得楼楼顶的俯角是,楼的楼顶的俯角是,已知两楼间的距离米,楼的高为10米,从楼的处测得楼的处的仰角是、、、、在同一平面内).
(1)求楼的高;
(2)小明发现无人机电量不足,仅能维持60秒的飞行时间,为了避免无人机掉落砸伤人,站在点的小明马上控制无人机从处匀速以5米秒的速度沿方向返航,无人机能安全返航吗?
答案解析部分
1.【答案】C
2.【答案】D
3.【答案】B
【解析】【解答】解: ,且,
,
故答案为:B.
【分析】直接利用特殊角的三角函数值结合锐角三角函数的关系的增减性,即可求解.
4.【答案】D
【解析】【解答】解:∵∠C=90°,
∴tanA= = ,
设BC=5x,AC=12x,
∴AB= =13x,
∴sinA= = = .
故答案为:D.
【分析】根据解直角三角形同角的三角函数关系得出结果;在Rt△ABC中,∠C=90°,tanA=,设BC=5x,AC=12x,根据勾股定理AB=13x,所以sinA= = =.
5.【答案】B
6.【答案】B
【解析】【解答】解:,,,,
A、 , 正确,符合同角三角函数的关系,不符合题意;
B、,错误,符合题意;
C、 ,正确,符合同角三角函数的关系,不符合题意;
D、 ,正确,不符合题意.
故答案为:B.
【分析】根据特殊角三角函数值可判定A、B、D,根据互余两角三角函数的关系判定C,解答即可。
7.【答案】D
8.【答案】A
9.【答案】B
【解析】【解答】解:设AB=3m,则BC=3m,
sin∠AOB=,
OB=7m,
故答案为:B.
【分析】设AB=3m,则BC=3m,根据sin∠AOB=,可得OB=7m,再根据,从而求解.
10.【答案】C
【解析】【解答】解:如图,连接AC,过C作CD⊥AB于点D.
观察易发现,AC=BC,
∴△ABC是等腰三角形.
∵CD⊥AB,
∴AD=BD,D点在格点上,
∴CD=,BD==.
∴tan∠ABC===.
故答案为:C.
【分析】连接AC,观察发现AC=BC得△ACB是等腰三角形,作垂线CD,可知D为AB中点,也为格点. 从而可利用勾股定理求出CD和BD的长,进而可求得答案. 注意网格中线段长要构造直角三角形并利用勾股定理来求.
11.【答案】60
12.【答案】105°
13.【答案】
14.【答案】
【解析】【解答】解:如图,作直线BG,
∵四边形ABCD是边长为3的正方形,
∴BC=CD=3,∠BCD=90°,
由旋转的性质得CF=CG,∠FCG=90°,
∴∠BCD-∠ECF=∠FCG-∠ECF,
即∠DCF=∠BCG,
∴△BCG≌△DCF(SAS),
∴∠CBG=∠CDF,
∵∠CDF是定值,
∴点G在直线BG上运动,且,
根据垂线段最短得,当EG⊥BG时,EG的长最短,此时,
设EG=m(m>0),则BG=3m,
在Rt△BEG中,∵BE2=BG2+EG2,
∴4=m2+9m2,
解得,
∴EG的最小值为.
故答案为:.
【分析】作直线BG,由正方形的性质得BC=CD=3,∠BCD=90°,由旋转的性质得CF=CG,∠FCG=90°,由同角的余角相等得∠DCF=∠BCG,从而由SAS判断出△BCG≌△DCF,由全等三角形的性质得∠CBG=∠CDF,由于∠CDF是定值,故点G在直线BG上运动,且,根据垂线段最短得,当EG⊥BG时,EG的长最短,此时,设EG=m(m>0),则BG=3m,在Rt△BEG中,利用勾股定理建立方程,求解得出m的值,即可得出答案.
15.【答案】(5-5)
16.【答案】(1)解:原式=
=
=
(2)解:∵
∴
原式=
∴
∴
【解析】【分析】(1)将特殊角的三角函数代入原式,然后根据二次根式的计算法则计算即可;
(2)根据题意得到将其代入原式即可求出b的值,进而即可求出a的值.
17.【答案】(1)解:过点C作CM⊥AB,如图,
在中,
设
∴
∴
(2)解:由(1)知:
∴
∵
∴
∴
∴.
【解析】【分析】(1)过点C作CM⊥AB,根据题意得到,设利用勾股定理求出AC的长度,进而即可求解;
(2)由(1)知:进而求出MB的长度,根据勾股定理列方程 解方程即可求解.
18.【答案】(1)证明:∵AB是☉O的直径,
∴∠ADB=90°.
∴∠DAB+∠DBA=90°.
∵=,∴∠AED=∠ABD.
∵∠PAD=∠AED,∴∠PAD=∠ABD.
∴∠BAD+∠PAD=∠BAD+∠ABD=90°,
即∠PAB=90°.
∴PA是☉O的切线.
(2)解:如图所示,连接OE,EB,
∵AE平分∠BAD,
∴∠DAE=∠BAE.
∴BE=DE=.
∴OE⊥BD.
∵OA=OE,
∴∠OEA=∠OAE.
∴∠DAE=∠AEO.
∴AD∥OE.
∵AB是☉O的直径,
∴∠ADF=∠BEF=90°.
∵=,∴∠DAE=∠DBE.
∴tan∠EBF=tan∠DAE=.
∴=.
∴EF=EB=1.
19.【答案】解:过点作交于,
则米,
在中,有米,
米
故BC米,
答:旗杆的高度约为米.
【解析】【分析】如图,过点D作DE⊥BC于E,在Rt△DEC中,DE=12,tan47°≈1.07,则可求出CE=12.8,再根据BE=1.5,BC=CE+BE即可求解。
20.【答案】(1)58
(2)解:过作与交于,过作与交于
∴四边形为矩形
∴90°,
∵148°
∴58°
在中90°
∵∴
∴
(3)解:过作,,
∴
在中=90°
∴60°
∵58°∴32°
∴60°-32°=28°
【解析】【解答】过点B作直线MN∥l,如图,
CD//l,
MN//l,
MN//CD,
故答案为:
【分析】(1)过点B作直线MN//l,利用平行四边形的性质即可解答;
(2)过作与交于,过作与交于,可得四边形ABEF为矩形,根据已知条件可求得∠1=58°,利用 ,求得CF的值,再根据线段的和差关系即可求得CE的值;
(3)过作, ,由 可求得 ,再求出∠DCN的余弦,进一步得 60°,进一步求得∠DCB的值.
21.【答案】(1)解:过点A作AF⊥CD,垂足为F,
由题意得:四边形ABDF是矩形,
∴米,米,
在中,,
(米),
(米),
楼CD的高为110米;
(2)解:无人机能安全返航,
理由:如图:
在中,,米,
(米),
由题意得:,
,
,
,
,
,
,
米,
无人机从E处匀速以5米/秒的速度沿EA方向返航,
无人机返航需要的时间(秒),
秒秒,
无人机能安全返航.
【解析】【分析】(1)过点A作AF⊥CD,垂足为F,易得四边形ABDF是矩形,由矩形的性质得AB=DF=10米,AF=BD=米,在Rt△AFC中,由∠CAF得正切函数可求出CF的长,进而根据CD=DF+CF可算出CD的长;
(2)无人机能安全返航,在Rt△AFC中,由含30°角直角三角形的性质可得AC=2CF=200米,然后根据平行线的性质角的和差可算出∠EAC=30°,由平角的定义算出∠AEC=75°,由三角形的内角和定理算出∠ACE=75°,则∠AEC=∠ACE,由等角对等边得AE=AC=200米,再根据路程除以速度等于时间算出无人机从E处匀速以5米/秒的速度沿EA方向返航需要的时间,将所算的时间与60秒比大小即可得出答案.
1 / 1
一、选择题
1.如图,是周长为36的等腰三角形,,,则的值为(
A. B. C. D.
2. 如图,△ABC的三个顶点都在方格纸的格点上,则cosA的值是( )
A. B. C. D.
3.锐角满足,且,则的取值范围为( )
A. B.
C. D.
4.在Rt△ABC中,∠C=90°,若tanA= ,则sinA=( )
A. B. C. D.
5. 在中,,,则的值为( )
A. B. C. D.
6.下列各式中不正确的是( ).
A. B.
C. D.
7. 在△ABC中,tan A=,cos B=,则∠C的度数是( )
A.30° B.45° C.60° D.90°
8. 如图所示,在Rt△ABC中,∠C=90°,D为BC边上一点,∠DAC=30°,BD=2,AB=2,则AC的长是( )
A. B.2 C.3 D.
9.如图1是第七届国际数学教育大会(ICME)会徽,选择其中两个相邻的直角三角形,恰好能组合得到如图2所示的四边形OABC.若AB=BC,sin∠AOB=,则tanC的值为( )
A. B. C. D.
10.由小正方形组成的网格如图,A,B,C三点都在格点上,则∠ABC的正切值为( )
A. B. C. D.
二、填空题
11. 已知为锐角,且,则 °.
12. 在△ABC中,若|2sin A-|与(-2cos B)2互为相反数,则∠C= .
13. 如图所示,已知△ABC的外接圆☉O的半径为3,AC=4,则sin B= .
14. 如图正方形的边长为3,E是上一点且,F是线段上的动点.连接,将线段绕点C逆时针旋转 90°得到,连接,则的最小值是 .
15. 如图所示,测量船以20 n mile/h的速度沿正东方向航行并对某海岛进行测量,测量船在A处测得海岛上观测点D位于北偏东15°方向上,观测点C位于北偏东45°方向上,航行半个小时到达B点,这时测得海岛上观测点C位于北偏西45°方向上,若CD与AB平行,则CD= n mile(计算结果不取近似值).
三、解答题
16.
(1)计算:2sin30°+cos30°·tan60°.
(2)已知,且a+b=20,求a,b的值.
17.已知:等腰三角形ABC中,AB=AC,∠A是锐角,且tanA=.
(1)求sinA;
(2)若BC=,求AB的长.
18. 如图所示,AB是☉O的直径,点E是劣弧BD上一点,∠PAD=∠AED,且DE=,AE平分∠BAD,AE与BD交于点F.
(1)求证:PA是☉O的切线;
(2)若tan∠DAE=,求EF的长.
19.如图,为了测量旗杆的高度,在离旗杆底部米的处,用高米的测角仪测得旗杆顶端处的仰角为求旗杆的高.精确到米
参考数据:,,
20.如图1,某款线上教学设备由底座,支撑臂,连杆,悬臂和安装在处的摄像头组成.如图2是该款设备放置在水平桌面上的示意图,已知支撑臂,,固定,可通过调试悬臂与连杆的夹角提高拍摄效果.
(1)当悬臂与桌面平行时,= °
(2)问悬臂端点到桌面的距离约为多少
(3)已知摄像头点到桌面的距离为30cm时拍摄效果较好,那么此时悬臂与连杆的夹角的度数约为多少 (参考数据:)
21.如图所示,无人机在生活中的使用越来越广泛,小明用无人机测量大楼的高度.无人机悬停在空中处,测得楼楼顶的俯角是,楼的楼顶的俯角是,已知两楼间的距离米,楼的高为10米,从楼的处测得楼的处的仰角是、、、、在同一平面内).
(1)求楼的高;
(2)小明发现无人机电量不足,仅能维持60秒的飞行时间,为了避免无人机掉落砸伤人,站在点的小明马上控制无人机从处匀速以5米秒的速度沿方向返航,无人机能安全返航吗?
答案解析部分
1.【答案】C
2.【答案】D
3.【答案】B
【解析】【解答】解: ,且,
,
故答案为:B.
【分析】直接利用特殊角的三角函数值结合锐角三角函数的关系的增减性,即可求解.
4.【答案】D
【解析】【解答】解:∵∠C=90°,
∴tanA= = ,
设BC=5x,AC=12x,
∴AB= =13x,
∴sinA= = = .
故答案为:D.
【分析】根据解直角三角形同角的三角函数关系得出结果;在Rt△ABC中,∠C=90°,tanA=,设BC=5x,AC=12x,根据勾股定理AB=13x,所以sinA= = =.
5.【答案】B
6.【答案】B
【解析】【解答】解:,,,,
A、 , 正确,符合同角三角函数的关系,不符合题意;
B、,错误,符合题意;
C、 ,正确,符合同角三角函数的关系,不符合题意;
D、 ,正确,不符合题意.
故答案为:B.
【分析】根据特殊角三角函数值可判定A、B、D,根据互余两角三角函数的关系判定C,解答即可。
7.【答案】D
8.【答案】A
9.【答案】B
【解析】【解答】解:设AB=3m,则BC=3m,
sin∠AOB=,
OB=7m,
故答案为:B.
【分析】设AB=3m,则BC=3m,根据sin∠AOB=,可得OB=7m,再根据,从而求解.
10.【答案】C
【解析】【解答】解:如图,连接AC,过C作CD⊥AB于点D.
观察易发现,AC=BC,
∴△ABC是等腰三角形.
∵CD⊥AB,
∴AD=BD,D点在格点上,
∴CD=,BD==.
∴tan∠ABC===.
故答案为:C.
【分析】连接AC,观察发现AC=BC得△ACB是等腰三角形,作垂线CD,可知D为AB中点,也为格点. 从而可利用勾股定理求出CD和BD的长,进而可求得答案. 注意网格中线段长要构造直角三角形并利用勾股定理来求.
11.【答案】60
12.【答案】105°
13.【答案】
14.【答案】
【解析】【解答】解:如图,作直线BG,
∵四边形ABCD是边长为3的正方形,
∴BC=CD=3,∠BCD=90°,
由旋转的性质得CF=CG,∠FCG=90°,
∴∠BCD-∠ECF=∠FCG-∠ECF,
即∠DCF=∠BCG,
∴△BCG≌△DCF(SAS),
∴∠CBG=∠CDF,
∵∠CDF是定值,
∴点G在直线BG上运动,且,
根据垂线段最短得,当EG⊥BG时,EG的长最短,此时,
设EG=m(m>0),则BG=3m,
在Rt△BEG中,∵BE2=BG2+EG2,
∴4=m2+9m2,
解得,
∴EG的最小值为.
故答案为:.
【分析】作直线BG,由正方形的性质得BC=CD=3,∠BCD=90°,由旋转的性质得CF=CG,∠FCG=90°,由同角的余角相等得∠DCF=∠BCG,从而由SAS判断出△BCG≌△DCF,由全等三角形的性质得∠CBG=∠CDF,由于∠CDF是定值,故点G在直线BG上运动,且,根据垂线段最短得,当EG⊥BG时,EG的长最短,此时,设EG=m(m>0),则BG=3m,在Rt△BEG中,利用勾股定理建立方程,求解得出m的值,即可得出答案.
15.【答案】(5-5)
16.【答案】(1)解:原式=
=
=
(2)解:∵
∴
原式=
∴
∴
【解析】【分析】(1)将特殊角的三角函数代入原式,然后根据二次根式的计算法则计算即可;
(2)根据题意得到将其代入原式即可求出b的值,进而即可求出a的值.
17.【答案】(1)解:过点C作CM⊥AB,如图,
在中,
设
∴
∴
(2)解:由(1)知:
∴
∵
∴
∴
∴.
【解析】【分析】(1)过点C作CM⊥AB,根据题意得到,设利用勾股定理求出AC的长度,进而即可求解;
(2)由(1)知:进而求出MB的长度,根据勾股定理列方程 解方程即可求解.
18.【答案】(1)证明:∵AB是☉O的直径,
∴∠ADB=90°.
∴∠DAB+∠DBA=90°.
∵=,∴∠AED=∠ABD.
∵∠PAD=∠AED,∴∠PAD=∠ABD.
∴∠BAD+∠PAD=∠BAD+∠ABD=90°,
即∠PAB=90°.
∴PA是☉O的切线.
(2)解:如图所示,连接OE,EB,
∵AE平分∠BAD,
∴∠DAE=∠BAE.
∴BE=DE=.
∴OE⊥BD.
∵OA=OE,
∴∠OEA=∠OAE.
∴∠DAE=∠AEO.
∴AD∥OE.
∵AB是☉O的直径,
∴∠ADF=∠BEF=90°.
∵=,∴∠DAE=∠DBE.
∴tan∠EBF=tan∠DAE=.
∴=.
∴EF=EB=1.
19.【答案】解:过点作交于,
则米,
在中,有米,
米
故BC米,
答:旗杆的高度约为米.
【解析】【分析】如图,过点D作DE⊥BC于E,在Rt△DEC中,DE=12,tan47°≈1.07,则可求出CE=12.8,再根据BE=1.5,BC=CE+BE即可求解。
20.【答案】(1)58
(2)解:过作与交于,过作与交于
∴四边形为矩形
∴90°,
∵148°
∴58°
在中90°
∵∴
∴
(3)解:过作,,
∴
在中=90°
∴60°
∵58°∴32°
∴60°-32°=28°
【解析】【解答】过点B作直线MN∥l,如图,
CD//l,
MN//l,
MN//CD,
故答案为:
【分析】(1)过点B作直线MN//l,利用平行四边形的性质即可解答;
(2)过作与交于,过作与交于,可得四边形ABEF为矩形,根据已知条件可求得∠1=58°,利用 ,求得CF的值,再根据线段的和差关系即可求得CE的值;
(3)过作, ,由 可求得 ,再求出∠DCN的余弦,进一步得 60°,进一步求得∠DCB的值.
21.【答案】(1)解:过点A作AF⊥CD,垂足为F,
由题意得:四边形ABDF是矩形,
∴米,米,
在中,,
(米),
(米),
楼CD的高为110米;
(2)解:无人机能安全返航,
理由:如图:
在中,,米,
(米),
由题意得:,
,
,
,
,
,
,
米,
无人机从E处匀速以5米/秒的速度沿EA方向返航,
无人机返航需要的时间(秒),
秒秒,
无人机能安全返航.
【解析】【分析】(1)过点A作AF⊥CD,垂足为F,易得四边形ABDF是矩形,由矩形的性质得AB=DF=10米,AF=BD=米,在Rt△AFC中,由∠CAF得正切函数可求出CF的长,进而根据CD=DF+CF可算出CD的长;
(2)无人机能安全返航,在Rt△AFC中,由含30°角直角三角形的性质可得AC=2CF=200米,然后根据平行线的性质角的和差可算出∠EAC=30°,由平角的定义算出∠AEC=75°,由三角形的内角和定理算出∠ACE=75°,则∠AEC=∠ACE,由等角对等边得AE=AC=200米,再根据路程除以速度等于时间算出无人机从E处匀速以5米/秒的速度沿EA方向返航需要的时间,将所算的时间与60秒比大小即可得出答案.
1 / 1
