数学人教A版(2019)选择性必修第三册6.3.1二项式定理 课件(共20张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第三册6.3.1二项式定理 课件(共20张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-21 21:48:40 | ||
图片预览







文档简介
(共20张PPT)
第6章计数原理
6.3.1 二项式定理
引
01
问题引入
最近我们学校举行知识竞赛,曾出现这样的题(有奖问题):
①今天是星期四,从明天起的第天是星期几?
本节我们将要学习一个在数学上有着广泛应用的(a+b)n展开式的问题,从而解决这个问题.
②今天是星期四,从明天起的第86天是星期几?
星期五
为了顺利的研究(a+b)n展开式的问题,我们先从学过的知识入手.
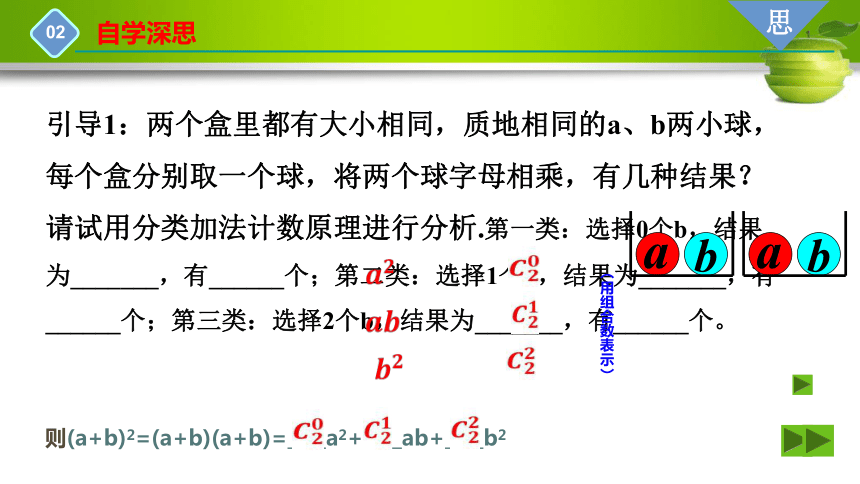
引导1:两个盒里都有大小相同,质地相同的a、b两小球,每个盒分别取一个球,将两个球字母相乘,有几种结果?请试用分类加法计数原理进行分析.第一类:选择0个b,结果为_______,有______个;第二类:选择1个b,结果为_______,有______个;第三类:选择2个b,结果为_______,有______个。
则(a+b)2=(a+b)(a+b)=____a2+____ab+____b2
思
02
自学深思
(用组合数表示)
第一类:
选择0个b
第二类:
选择1个b
第三类:
选择2个b
类比
取
0
个
b
项
系数
再来分析(a+b)3展开后有哪些项?各项的系数分别是什么?
取
1
个
b
取
2
个
b
取
3
个
b
(a+b)3=(a+b)(a+b)(a+b)
a3
a2b
ab2
b3
则(a+b)3=
各字母的指数之和是3
思
02
自学深思
观察各项的次数是?
根椐你发现的规律,你能写出(a+b)4展开吗?
(a+b)4=
(a+b)4=(a+b)(a+b)(a+b)(a+b)
思
02
自学深思
仿照:
都
不
取
b
项
系数
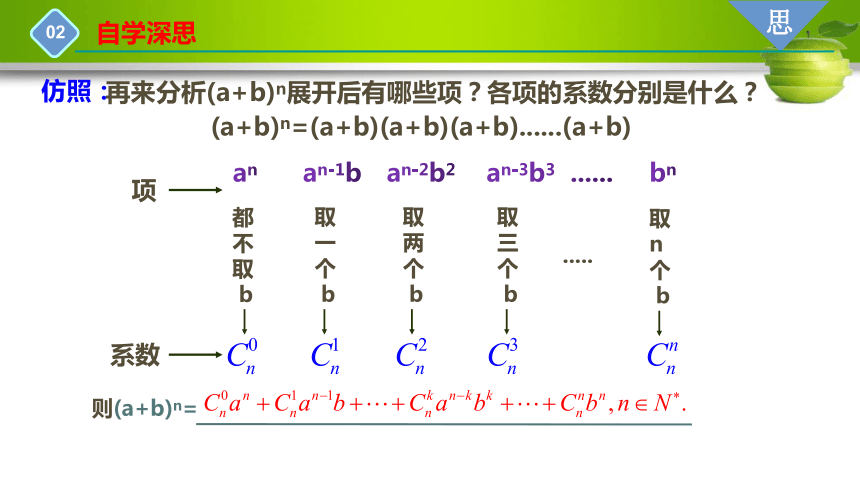
再来分析(a+b)n展开后有哪些项?各项的系数分别是什么?
取
一
个
b
取
两
个
b
取
三
个
b
取
n
个
b
(a+b)n=(a+b)(a+b)(a+b)......(a+b)
an
an-1b
an-2b2
an-3b3 ......
bn
则(a+b)n=
.....
思
02
自学深思
4. 归纳
n+1
k+1
二项式定理
二项式展开式
二项式系数
思
02
自学深思
k表示?
追问:每一项a与b的指数和为?a的指数按什么顺序排列?b 的呢?
k表示b的指数
你知道二项式定理是谁最先提出的吗?
杨辉三角
二项式定理虽是由牛顿16世纪提出的,但是我们中国杨辉早在11世纪发现,比西方早近500年左右。在人类科学历史中,根据英国人李约瑟教授的研究,中国在人类中早期的1000多年中,在科学技术上就已经取得1000多个世界第一。这是中国的辉煌与荣耀,也是中国快速发展崛起的重要基础。
二项式定理
试一试
思
02
自学深思
×
×
议
03
合作应用
注意:分式或者根式,一般要化成指数幂的形式
解:
追问:常数项是第几项?
第4项
今天是星期四,从明天起的第天是星期几?
解决课前的思考题:
议
03
合作应用
(1)求(1+2x)7的展开式中的第4项的系数;
∴ 第4项的二项式系数是35
解:(1)(1+2x)7的展开式的第4项是
T3+1 =·17-3· (2x)3
=×23x3
=35× 8× x3
=280x3
因此,展开式第4项的系数是280.
议
03
合作应用
追问:求(1+2x)7的展开式中的第4项的二项式系数.
通项公式
练
04
巩固练习
结
05
课堂小结
今天这节课你的收获是什么?
(1)二项式定理
(2)对二项式定理的理解和掌握,要从项数、系数、指数、通项等方面的特征去熟悉他的展开式.通项公式
在解题时应用较多,因而显得尤其重要,但必须注意,它是
的二项式展开式的第
项,而不是第 项.
结
05
课堂小结
测
06
拓展提高
解:
求 的展开式中 的系数。
的展开式的通项:
根据题意,得
因此, 的系数是
例2(2)
通项公式
变式:能否找到展开式中的常数项
议
03
合作应用
谢 谢!
第6章计数原理
6.3.1 二项式定理
引
01
问题引入
最近我们学校举行知识竞赛,曾出现这样的题(有奖问题):
①今天是星期四,从明天起的第天是星期几?
本节我们将要学习一个在数学上有着广泛应用的(a+b)n展开式的问题,从而解决这个问题.
②今天是星期四,从明天起的第86天是星期几?
星期五
为了顺利的研究(a+b)n展开式的问题,我们先从学过的知识入手.
引导1:两个盒里都有大小相同,质地相同的a、b两小球,每个盒分别取一个球,将两个球字母相乘,有几种结果?请试用分类加法计数原理进行分析.第一类:选择0个b,结果为_______,有______个;第二类:选择1个b,结果为_______,有______个;第三类:选择2个b,结果为_______,有______个。
则(a+b)2=(a+b)(a+b)=____a2+____ab+____b2
思
02
自学深思
(用组合数表示)
第一类:
选择0个b
第二类:
选择1个b
第三类:
选择2个b
类比
取
0
个
b
项
系数
再来分析(a+b)3展开后有哪些项?各项的系数分别是什么?
取
1
个
b
取
2
个
b
取
3
个
b
(a+b)3=(a+b)(a+b)(a+b)
a3
a2b
ab2
b3
则(a+b)3=
各字母的指数之和是3
思
02
自学深思
观察各项的次数是?
根椐你发现的规律,你能写出(a+b)4展开吗?
(a+b)4=
(a+b)4=(a+b)(a+b)(a+b)(a+b)
思
02
自学深思
仿照:
都
不
取
b
项
系数
再来分析(a+b)n展开后有哪些项?各项的系数分别是什么?
取
一
个
b
取
两
个
b
取
三
个
b
取
n
个
b
(a+b)n=(a+b)(a+b)(a+b)......(a+b)
an
an-1b
an-2b2
an-3b3 ......
bn
则(a+b)n=
.....
思
02
自学深思
4. 归纳
n+1
k+1
二项式定理
二项式展开式
二项式系数
思
02
自学深思
k表示?
追问:每一项a与b的指数和为?a的指数按什么顺序排列?b 的呢?
k表示b的指数
你知道二项式定理是谁最先提出的吗?
杨辉三角
二项式定理虽是由牛顿16世纪提出的,但是我们中国杨辉早在11世纪发现,比西方早近500年左右。在人类科学历史中,根据英国人李约瑟教授的研究,中国在人类中早期的1000多年中,在科学技术上就已经取得1000多个世界第一。这是中国的辉煌与荣耀,也是中国快速发展崛起的重要基础。
二项式定理
试一试
思
02
自学深思
×
×
议
03
合作应用
注意:分式或者根式,一般要化成指数幂的形式
解:
追问:常数项是第几项?
第4项
今天是星期四,从明天起的第天是星期几?
解决课前的思考题:
议
03
合作应用
(1)求(1+2x)7的展开式中的第4项的系数;
∴ 第4项的二项式系数是35
解:(1)(1+2x)7的展开式的第4项是
T3+1 =·17-3· (2x)3
=×23x3
=35× 8× x3
=280x3
因此,展开式第4项的系数是280.
议
03
合作应用
追问:求(1+2x)7的展开式中的第4项的二项式系数.
通项公式
练
04
巩固练习
结
05
课堂小结
今天这节课你的收获是什么?
(1)二项式定理
(2)对二项式定理的理解和掌握,要从项数、系数、指数、通项等方面的特征去熟悉他的展开式.通项公式
在解题时应用较多,因而显得尤其重要,但必须注意,它是
的二项式展开式的第
项,而不是第 项.
结
05
课堂小结
测
06
拓展提高
解:
求 的展开式中 的系数。
的展开式的通项:
根据题意,得
因此, 的系数是
例2(2)
通项公式
变式:能否找到展开式中的常数项
议
03
合作应用
谢 谢!
