化学人教版(2019)选择性必修2 3.1.2晶胞(共37张ppt)
文档属性
| 名称 | 化学人教版(2019)选择性必修2 3.1.2晶胞(共37张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 化学 | ||
| 更新时间 | 2024-03-21 00:00:00 | ||
图片预览






文档简介
(共37张PPT)
第三章 晶体结构与性质
第一节 物质的聚集状态与晶体常识
第2课时 晶胞
【思考】晶体为什么具有如此漂亮完美的外形?
内部微粒在三维空间里呈周期性有序排列
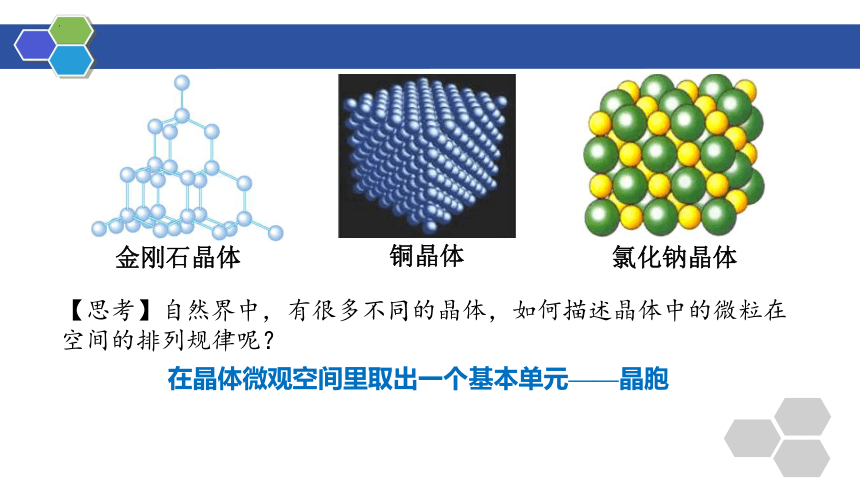
【思考】自然界中,有很多不同的晶体,如何描述晶体中的微粒在空间的排列规律呢?
在晶体微观空间里取出一个基本单元——晶胞
金刚石晶体
铜晶体
氯化钠晶体
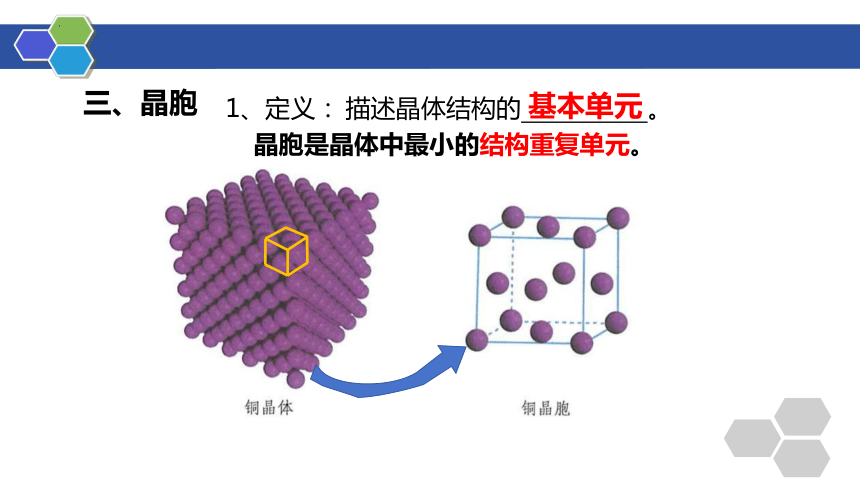
三、晶胞
描述晶体结构的 。
1、定义:
基本单元
晶胞是晶体中最小的结构重复单元。
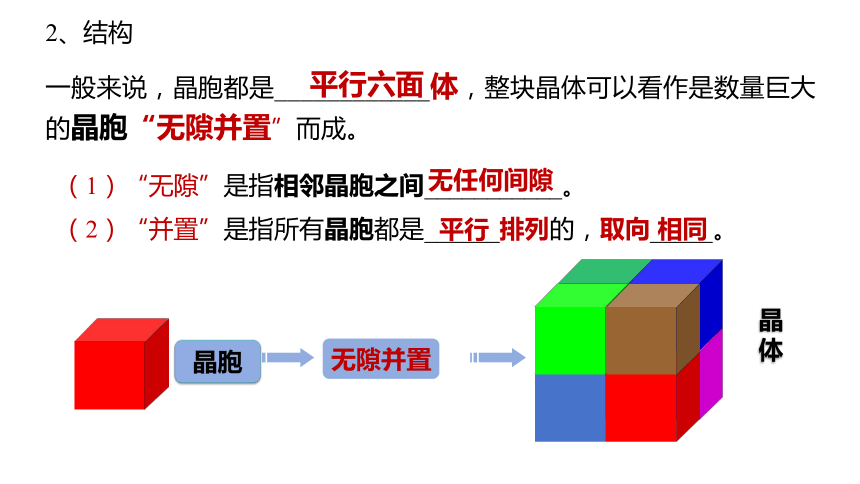
2、结构
一般来说,晶胞都是____________体,整块晶体可以看作是数量巨大的晶胞“无隙并置”而成。
平行六面
(1)“无隙”是指相邻晶胞之间___________。
无任何间隙
(2)“并置”是指所有晶胞都是______排列的,取向_____。
平行
相同
无隙并置
晶体
晶胞
晶胞
【思考】观察晶体中晶胞的结构关系,你能总结出什么规律?
晶体
晶体中所有晶胞的______及其内部的_________、_____及_________是完全
相同的。
形状
原子种类
个数
几何排列
(包括取向)
三套各四根平行棱
三套各两个平行面
8个顶角相同
A
【思考】判断下列六面体哪个是晶胞?
B不符合
8个顶角相同
C不符合
三套各4根平行棱
D不符合
三套各两个平行面
有几个顶角?
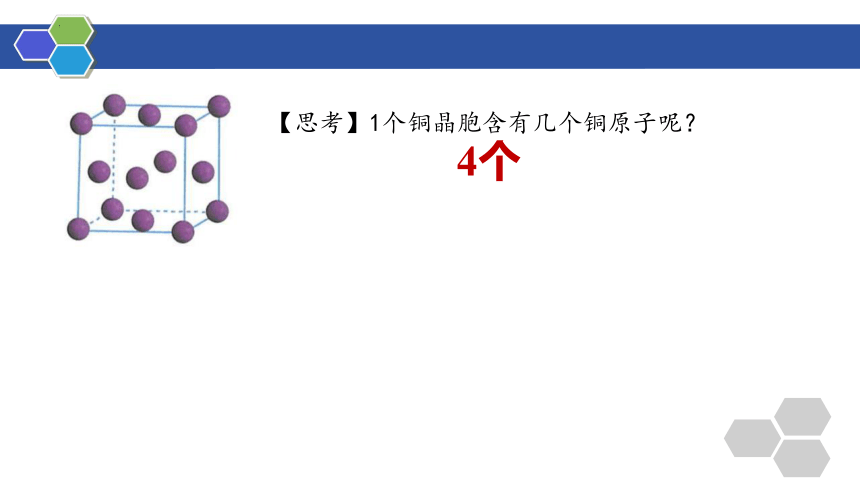
【思考】1个铜晶胞含有几个铜原子呢?
4个
战
均摊法
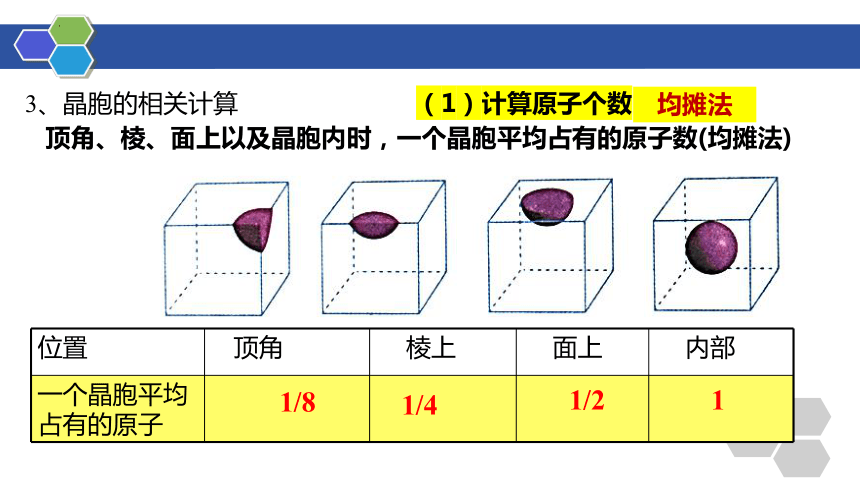
3、晶胞的相关计算
顶角、棱、面上以及晶胞内时,一个晶胞平均占有的原子数(均摊法)
位置 顶角 棱上 面上 内部
一个晶胞平均占有的原子
1/8
1/4
1/2
1
(1)计算原子个数
8
1
8×
2
1
6×
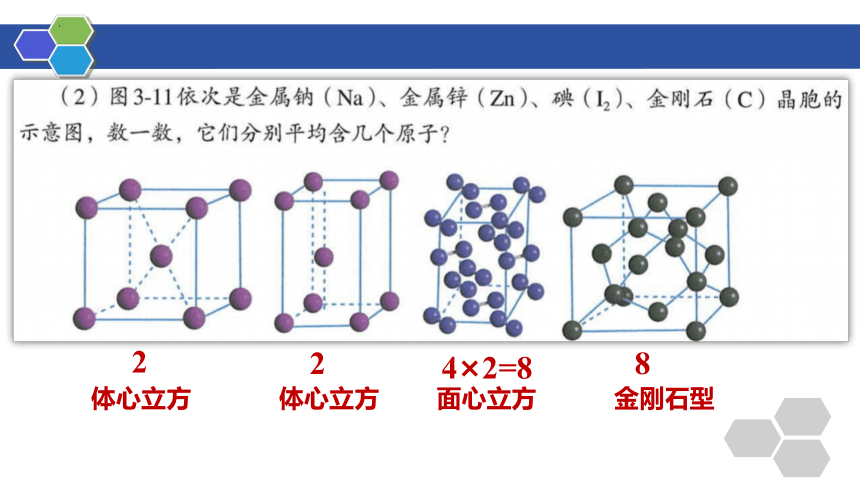
常见的晶胞
类型 简单立方 体心立方 面心立方
结构特点 在平面六面体的8个顶角上有粒子 除8个顶角上有粒子外,平行六面体的体心上还有1个粒子 除8个顶角上有粒子外,平行六面体的6个面的面心上均有1个粒子
一个晶胞的原子数
1
2
4
2
2
4×2=8
8
体心立方
体心立方
面心立方
金刚石型
【思考】氯化钠的晶胞,它含有几个Na+?
几个Cl—?
Na+数目
= 12× + 1 =4
4
1
Cl—数目
= 6×
2
1
+ 8× =4
8
1
(2)求化学式
化学式为NaCl
一个晶胞含4个Na+和4个Cl-
一般地,晶体的化学式表示的是晶体(也可以说是每个晶胞)中各类原子或离子数目的最简整数比。
球棍模型
该晶胞中各原子的数目为,已知该晶体的化学式为XnYmZq:
X=____,Y=____, Z=____,D的化学式为 。
1
3
1
XY3Z
X, Y, Z
晶胞不一定都取平行六面体
晶胞不一定都取平行六面体
以下晶胞如何利用均摊法计算原子数?
位置 顶角 竖直棱 面上 内部
份额
1/6
1/3
1/2
1
以下晶胞如何利用均摊法计算原子数?
位置 顶角 水平棱 竖直棱 内部
份额
1/12
1/4
1
1/6
【思考】①科学家是如何用证实晶体是周期重复排列的结构呢?
②怎么知道晶胞的大小、形状、取向和各个原子的位置呢?
O
Fe
I2
当单一波长的X射线通过晶体时,X射线和晶体中的电子相互作用,在记录仪上形成衍射图谱。人们对衍射图的数据进行处理,即可获得晶体结构的有关信息。
X射线管
铅板
晶体样品
记录仪
二、晶体结构的测定——X射线衍射实验
2θ/°
非晶态SiO2
晶态SiO2
明锐的衍射峰
分立的斑点
衍射图
计算获得
晶胞形状和大小
分子或原子在微观空间有序排列呈现的对称类型
⒉、X射线衍射图谱的应用
①X射线衍射实验获得晶胞信息
晶体的周期性结构
衍射图
计算获得
晶胞形状和大小
分子或原子在微观空间有序排列呈现的对称类型
原子在晶胞里的数目和位置
结合晶体化学组成的信息推出原子之间的相互关系
②X射线衍射实验获得分子信息
根据原子坐标,可以计算原子间的距离,判断哪些原子之间存在化学键,确定键长和键角,得出分子的空间结构。
乙酸晶胞
(3)求晶胞密度:先用均摊法计算晶胞中各粒子的数目,再代入公式
设晶胞的边长为a cm
V
m
ρ=
m=n·M
NA
N
n=
ρ=
N ·M
NA ·V
单个/1mol晶胞所含粒子的质量
单个/1mol
晶胞的体积
ρ=
N ·M
NA ·a3
单位换算: 1cm=107nm=1010pm(注意密度和边长的单位要统一)
立方体晶胞中常用关系:
面对角线与边长关系:
边长a
l
d
体对角线与边长关系:
l
a
a
勾股定理:
l2 = a 2 + a 2 =2a 2
d2 = a 2 + l 2 =3a 2
已知金属钋是简单立方堆积,钋原子半径为r cm,计算:钋晶胞棱长a;钋的密度ρ。
①棱长a = 2r
②密度
简单立方堆积
①体对角线=4r
②密度
体心立方紧密堆积
已知金属钾是体心立方紧密堆积,钾原子半径为r cm,请计算:用r表示钾晶胞棱长a;晶体的密度ρ。
已知金属金是面心立方紧密堆积,金原子半径为r cm,计算:金晶胞棱长a;金晶体的密度ρ。
①面对角线 = 4r
②密度
面心立方紧密堆积
(4)求配位数
在晶体中,与某个原子(或离子)距离最近且相等的其他原子(或离子)的个数,叫做这种原子(或离子)的配位数。
AlF3结构属于立方晶系,晶胞中F—和Al3+位置如图所示,F—的配位数为 。
2
在左侧晶体中每个Ti周围与它距离最近且相等的Ti的个数为____。
在右侧晶体中1个Co原子周围距离最近的O原子数目为___个。
6
12
(5)晶胞中原子的分数坐标
例1.Zn与S形成某种化合物的晶胞如图所示。
(1)以晶胞参数为单位长度建立的坐标系可以表示晶胞中各原子的位置,称作原子分数坐标。例如图中原子1的坐标为(0,0,0),则原子2的坐标为 。
例2:钙钛矿晶体的晶胞结构如图所示,则该晶体的化学式为 ;晶胞中的原子可用x、y、z组成的三数组来表示它在晶胞中的位置,称为原子分数坐标。已知A的坐标为(0,0,0) , B的坐标为(0 ,1/2 , 0),则Ca的原子坐标为 。
CaTiO3
谢谢观看
(6)晶体空间利用率的计算
晶体空间利用率=
晶胞(立方体)体积
晶胞粒子(球体)总体积
×100%
先用均摊法计算出晶胞中的粒子数目
空间利用率是指构成晶体的原子、离子或分子在整个晶体空间中所占的体积百分比,也叫空间占有率。
已知金属钋是简单立方堆积,钋原子半径为r cm,晶胞中有 个钋原子
①棱长a = 2r
②利用率=
简单立方堆积
= 52%
1
棱长
①立方体对角线=4r
体心立方紧密堆积
已知金属钾是体心立方紧密堆积,钾原子半径为r cm,请计算:用r表示钾晶胞棱长a;晶体的密度。
②利用率=
已知金属金是面心立方紧密堆积,金原子半径为r cm,计算:金晶胞棱长;金晶体的密度ρ。
①面对角线 = 4r
棱长
面心立方紧密堆积
②利用率=
第三章 晶体结构与性质
第一节 物质的聚集状态与晶体常识
第2课时 晶胞
【思考】晶体为什么具有如此漂亮完美的外形?
内部微粒在三维空间里呈周期性有序排列
【思考】自然界中,有很多不同的晶体,如何描述晶体中的微粒在空间的排列规律呢?
在晶体微观空间里取出一个基本单元——晶胞
金刚石晶体
铜晶体
氯化钠晶体
三、晶胞
描述晶体结构的 。
1、定义:
基本单元
晶胞是晶体中最小的结构重复单元。
2、结构
一般来说,晶胞都是____________体,整块晶体可以看作是数量巨大的晶胞“无隙并置”而成。
平行六面
(1)“无隙”是指相邻晶胞之间___________。
无任何间隙
(2)“并置”是指所有晶胞都是______排列的,取向_____。
平行
相同
无隙并置
晶体
晶胞
晶胞
【思考】观察晶体中晶胞的结构关系,你能总结出什么规律?
晶体
晶体中所有晶胞的______及其内部的_________、_____及_________是完全
相同的。
形状
原子种类
个数
几何排列
(包括取向)
三套各四根平行棱
三套各两个平行面
8个顶角相同
A
【思考】判断下列六面体哪个是晶胞?
B不符合
8个顶角相同
C不符合
三套各4根平行棱
D不符合
三套各两个平行面
有几个顶角?
【思考】1个铜晶胞含有几个铜原子呢?
4个
战
均摊法
3、晶胞的相关计算
顶角、棱、面上以及晶胞内时,一个晶胞平均占有的原子数(均摊法)
位置 顶角 棱上 面上 内部
一个晶胞平均占有的原子
1/8
1/4
1/2
1
(1)计算原子个数
8
1
8×
2
1
6×
常见的晶胞
类型 简单立方 体心立方 面心立方
结构特点 在平面六面体的8个顶角上有粒子 除8个顶角上有粒子外,平行六面体的体心上还有1个粒子 除8个顶角上有粒子外,平行六面体的6个面的面心上均有1个粒子
一个晶胞的原子数
1
2
4
2
2
4×2=8
8
体心立方
体心立方
面心立方
金刚石型
【思考】氯化钠的晶胞,它含有几个Na+?
几个Cl—?
Na+数目
= 12× + 1 =4
4
1
Cl—数目
= 6×
2
1
+ 8× =4
8
1
(2)求化学式
化学式为NaCl
一个晶胞含4个Na+和4个Cl-
一般地,晶体的化学式表示的是晶体(也可以说是每个晶胞)中各类原子或离子数目的最简整数比。
球棍模型
该晶胞中各原子的数目为,已知该晶体的化学式为XnYmZq:
X=____,Y=____, Z=____,D的化学式为 。
1
3
1
XY3Z
X, Y, Z
晶胞不一定都取平行六面体
晶胞不一定都取平行六面体
以下晶胞如何利用均摊法计算原子数?
位置 顶角 竖直棱 面上 内部
份额
1/6
1/3
1/2
1
以下晶胞如何利用均摊法计算原子数?
位置 顶角 水平棱 竖直棱 内部
份额
1/12
1/4
1
1/6
【思考】①科学家是如何用证实晶体是周期重复排列的结构呢?
②怎么知道晶胞的大小、形状、取向和各个原子的位置呢?
O
Fe
I2
当单一波长的X射线通过晶体时,X射线和晶体中的电子相互作用,在记录仪上形成衍射图谱。人们对衍射图的数据进行处理,即可获得晶体结构的有关信息。
X射线管
铅板
晶体样品
记录仪
二、晶体结构的测定——X射线衍射实验
2θ/°
非晶态SiO2
晶态SiO2
明锐的衍射峰
分立的斑点
衍射图
计算获得
晶胞形状和大小
分子或原子在微观空间有序排列呈现的对称类型
⒉、X射线衍射图谱的应用
①X射线衍射实验获得晶胞信息
晶体的周期性结构
衍射图
计算获得
晶胞形状和大小
分子或原子在微观空间有序排列呈现的对称类型
原子在晶胞里的数目和位置
结合晶体化学组成的信息推出原子之间的相互关系
②X射线衍射实验获得分子信息
根据原子坐标,可以计算原子间的距离,判断哪些原子之间存在化学键,确定键长和键角,得出分子的空间结构。
乙酸晶胞
(3)求晶胞密度:先用均摊法计算晶胞中各粒子的数目,再代入公式
设晶胞的边长为a cm
V
m
ρ=
m=n·M
NA
N
n=
ρ=
N ·M
NA ·V
单个/1mol晶胞所含粒子的质量
单个/1mol
晶胞的体积
ρ=
N ·M
NA ·a3
单位换算: 1cm=107nm=1010pm(注意密度和边长的单位要统一)
立方体晶胞中常用关系:
面对角线与边长关系:
边长a
l
d
体对角线与边长关系:
l
a
a
勾股定理:
l2 = a 2 + a 2 =2a 2
d2 = a 2 + l 2 =3a 2
已知金属钋是简单立方堆积,钋原子半径为r cm,计算:钋晶胞棱长a;钋的密度ρ。
①棱长a = 2r
②密度
简单立方堆积
①体对角线=4r
②密度
体心立方紧密堆积
已知金属钾是体心立方紧密堆积,钾原子半径为r cm,请计算:用r表示钾晶胞棱长a;晶体的密度ρ。
已知金属金是面心立方紧密堆积,金原子半径为r cm,计算:金晶胞棱长a;金晶体的密度ρ。
①面对角线 = 4r
②密度
面心立方紧密堆积
(4)求配位数
在晶体中,与某个原子(或离子)距离最近且相等的其他原子(或离子)的个数,叫做这种原子(或离子)的配位数。
AlF3结构属于立方晶系,晶胞中F—和Al3+位置如图所示,F—的配位数为 。
2
在左侧晶体中每个Ti周围与它距离最近且相等的Ti的个数为____。
在右侧晶体中1个Co原子周围距离最近的O原子数目为___个。
6
12
(5)晶胞中原子的分数坐标
例1.Zn与S形成某种化合物的晶胞如图所示。
(1)以晶胞参数为单位长度建立的坐标系可以表示晶胞中各原子的位置,称作原子分数坐标。例如图中原子1的坐标为(0,0,0),则原子2的坐标为 。
例2:钙钛矿晶体的晶胞结构如图所示,则该晶体的化学式为 ;晶胞中的原子可用x、y、z组成的三数组来表示它在晶胞中的位置,称为原子分数坐标。已知A的坐标为(0,0,0) , B的坐标为(0 ,1/2 , 0),则Ca的原子坐标为 。
CaTiO3
谢谢观看
(6)晶体空间利用率的计算
晶体空间利用率=
晶胞(立方体)体积
晶胞粒子(球体)总体积
×100%
先用均摊法计算出晶胞中的粒子数目
空间利用率是指构成晶体的原子、离子或分子在整个晶体空间中所占的体积百分比,也叫空间占有率。
已知金属钋是简单立方堆积,钋原子半径为r cm,晶胞中有 个钋原子
①棱长a = 2r
②利用率=
简单立方堆积
= 52%
1
棱长
①立方体对角线=4r
体心立方紧密堆积
已知金属钾是体心立方紧密堆积,钾原子半径为r cm,请计算:用r表示钾晶胞棱长a;晶体的密度。
②利用率=
已知金属金是面心立方紧密堆积,金原子半径为r cm,计算:金晶胞棱长;金晶体的密度ρ。
①面对角线 = 4r
棱长
面心立方紧密堆积
②利用率=
