人教版七下第七章平面直角坐标系单元测试卷(含解析)
文档属性
| 名称 | 人教版七下第七章平面直角坐标系单元测试卷(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-22 07:53:26 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
人教版七下第七章平面直角坐标系单元测试卷
时间100分钟 满分120分
一、选择题(每小题3分,共36分)
1.第19届亚运会2023年9月在浙江省杭州市举行.以下能够准确表示杭州市地理位置的是( )
A.距离兴化市370公 B.在浙江省 C.在兴化市的南方 D.东经,北纬
2.在数轴上,用有序数对表示点的平移,若得到的数为1,得到的数为3,则得到的数为( ).
A.8 B. C.2 D.
3.点的坐标满足,那么点在( )
A.纵轴上 B.横轴上
C.原点 D.纵轴或横轴上
4.已知点在轴上,则的值为( )
A. B.3 C.0 D.
5.已知点 P 在第四象限,且到 x 轴的距离为 3,到 y 轴的距离为 2,则点 P 的坐标是( )
A. B. C. D.
6.若点的坐标是,且平行于轴,则点的坐标为( )
A. B.或
C. D.或
7.象棋起源于中国,中国象棋文化历史悠久.如图,是中国象棋棋盘的一部分,若“帅”位于点,“炮”位于点上,则“兵”位于点( )上.
A. B. C. D.
8.小明从学校出发,步行去少年宫(如图),行走路线正确的是( )
A.向南偏东行走600米 B.向南偏西行走600米
C.向南偏东行走600米 D.向南偏西行走600米
9.在平面直角坐标系中,将点向左平移3个单位,再向下平移1个单位得到,则点的坐标为( )
A. B. C. D.
10.在平面直角坐标系中,已知,将线段平移后得到线段,点A、B的对应点分别是点、. 若点的坐标为,则点的坐标为( ).
A. B. C. D.
11.如图,三角形ABC沿着BC所在直线向右平移a个单位长度得到三角形DEF(点E在点C的左侧).下列判断正确的是( )
结论Ⅰ:若BF=8,EC=4,则a的值为2;
结论Ⅱ:连接AD,若三角形ABC的周长为18,四边形ABFD的周长为22,则a的值为4.
A.Ⅰ和Ⅱ都对 B.Ⅰ和Ⅱ都不对 C.Ⅰ不对Ⅱ对 D.Ⅰ对Ⅱ不对
12.如图,在平面直角坐标系中,动点按箭头所示的方向做折线运动,第一次从原点运动到,第二次从运动到,第三次从运动到,第四次从运动到,第五次从运动到,第六次从运动到……,按这样的运动规律(向右始终保持运动一个单位长度,向上或向下比前一次的向下或向上都多运动一个单位长度),经过第2023次,点的坐标是( )
A. B. C. D.
二、填空题(每小题3分,共24分)
13.如图,雷达探测器在一次探测中发现了三个目标A、B、C,点A、B的坐标分别表示为,则点C的坐标表示为 .
14.已知点到两坐标轴的距离相等,则 .
15.若点向上平移3个单位后得到的点在x轴上,则m的值为 .
16.平面直角坐标系中,已知点,,当线段有最小值时, .
17.如图是轰炸机机群的一个飞行队形,若轰炸机A、B的坐标分别是,则轰炸机C的坐标为 .
18.如图,在平面直角坐标系中,长方形的边与轴平行且,,点坐标为,沿某一方向平移后,点的对应点的坐标为,则点的坐标为 .
19.已知点,点,点是坐标轴上一动点,若三角形的面积为,则的坐标为 .
20.如图,在平面直角坐标系中,设一动点自处向下运动1个单位长度至处,然后向左运动2个单位长度至处,再向上运动2个单位长度至处,再向左运动2个单位长度至处,再向下运动2个单位长度至处,,如此继续运动下去,设,,2,3,,则的坐标是 .
三、解答题(共60分)
21.(8分)下图是游乐园一角的平面示意图,图中1个单位长度表示100m.
(1)如果用有序数对(3,2)表示跳跳床的位置,填写下列两个游乐设施的位置:跷跷板________,碰碰车________;
(2)秋千的位置是(4,5),请在图中标出来;
(3)旋转木马在大门以东500m,再往北200m处,请在图中标出来.
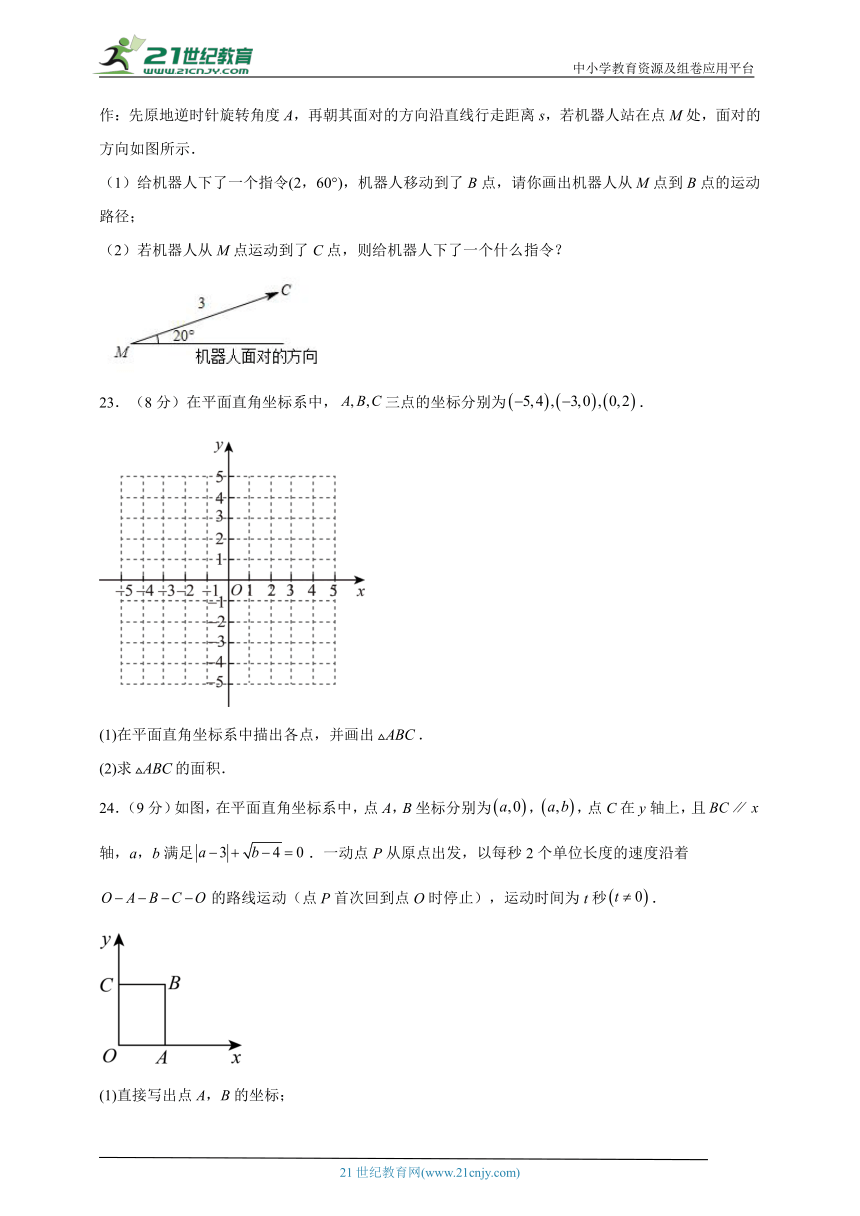
22.(8分)根据指令(s,A)(说明:s≥0,单位:厘米;0°≤A<180°),机器人在平面上能完成下列动作:先原地逆时针旋转角度A,再朝其面对的方向沿直线行走距离s,若机器人站在点M处,面对的方向如图所示.
(1)给机器人下了一个指令(2,60°),机器人移动到了B点,请你画出机器人从M点到B点的运动路径;
(2)若机器人从M点运动到了C点,则给机器人下了一个什么指令?
23.(8分)在平面直角坐标系中,三点的坐标分别为.
(1)在平面直角坐标系中描出各点,并画出.
(2)求的面积.
24.(9分)如图,在平面直角坐标系中,点A,B坐标分别为,,点C在y轴上,且轴,a,b满足.一动点P从原点出发,以每秒2个单位长度的速度沿着的路线运动(点P首次回到点O时停止),运动时间为t秒.
(1)直接写出点A,B的坐标;
(2)点P在运动过程中,是否存在点P到x轴的距离为个单位长度的情况,若存在,求出点P的坐标,若不存在,请说明理由.
25.(9分)如图,点A的坐标为,点B在y轴上,将三角形沿x轴负方向平移,平移后的图形为三角形,且点C的坐标为.
(1)点D的坐标为__________;
(2)在四边形中,点P从点B出发,沿移动,若点P的速度为1个单位长度/秒,运动时间为t秒,回答下列问题:
①求点P在运动过程中的坐标(用含t的式子表示,写出过程);
②当点P运动到时,若,请直接写出的度数.
26.(9分)如图,已知点,满足.将线段先向上平移4个单位,再向右平移1个单位后得到线段,连接,.
(1)直接写出点A和点B的坐标;
(2)点M从O点出发,以每秒1个单位的速度向上平移运动.设运动时间为t秒,当t为多少时,四边形的面积等于?
(3)在(2)的条件下,点M从O点出发的同时,点N从B点出发,以每秒个单位的速度向左平移运动,设射线交y轴于点E.在运动过程中的值是否会发生变化?若不变,请求出它的值;若变化,请说明理由.
27.(9分)如图,在平面直角坐标系中,A,B坐标分别为、,且a,b满足:,现同时将点A,B分别向下平移4个单位,再向左平移1个单位,分别得到点A,B的对应点C,D,连接.
(1)求C,D两点的坐标及四边形的面积;
(2)点P是线段上的一个动点,连接,当点P在上移动时(不与B,D重合),的值是否发生变化,并说明理由;
(3)已知点M在y轴上,且点D在的外部,连接,若的面积与四边形的面积相等,求点M的坐标.
第七章单元测试卷参考答案
1.D[提示:由题意可知,东经,北纬能够准确表示杭州市地理位置,其他都不能准确表示杭州市地理位置.故选:D.]
2.B[提示: 用有序数对表示点的平移,得到的数为1,得到的数为3,
数轴上的数向左边平移个单位得到的数为
数轴上的数向右边平移个单位得到的数为
可表示数轴上的数向左边平移个单位得到的数是
故选:]
3.C[提示:由,得
,,
∴点在原点.
故选:C.]
4.B[提示:点在轴上,
,解得.
故选:B.]
5.D[提示:点在第四象限,且到轴的距离为3,到轴的距离为2,
点的横坐标是2,纵坐标是,
点的坐标是.
故选:D]
6.D[提示:已知点,轴,且,则点的坐标为或,
故选:D]
7.A[提示:∵“兵”在“炮”的上面,
∴“兵”的纵坐标是,
∵“兵”在“帅”的左面第一格上,
∴“兵”的横坐标是,
∴“兵”的坐标是,
故选:.]
8.B[提示:小明从学校出发,步行去少年宫行走路线是:向南偏西行走米.
故选:B.]
9.C[提示:∵向左平移3个单位长度后,再向下平移1个单位长度,
∴,,
∴点的坐标为,
故选:C.]
10.B[提示:∵,,
∴点向右平移4个单位,向下平移3个单位得点,
∴点向右平移4个单位,向下平移3个单位得点.
故选:B.]
11.D[提示:∵三角形ABC沿着BC所在直线向右平移a个单位长度得到三角形DEF,
∴BE=CF=a,
∵BF=BE+CE+CF,BF=8,EC=4,
∴8=a+4+a,
∴a=2,故结论Ⅰ正确;
∵三角形ABC沿着BC所在直线向右平移a个单位长度得到三角形DEF,
∴AC=DF,
∵四边形ABFD的周长为22,
∴AB+BC+CF+DF+AD=22,
∴AB+BC+CF+AC+AD=22,
∵三角形ABC的周长为18,
∴AB+BC+AC=18,
∴18+CF+AD=22,即18+a+a=22,
∴a=2,故结论(Ⅱ)不正确,
∴Ⅰ对Ⅱ不对,
故选:D.]
12.C[提示:根据题意可得,
第一次从原点运动到,
第二次从运动到,
第三次从运动到,
第四次从运动到,
第五次从运动到,
第六次从运动到,
第七次从运动到,
第八次从运动到,
第九次从运动到,
…
∴第一次和第二次的横坐标都为1,
第三次和第四次的横坐标都为2,
第五次和第六次的横坐标都为3,
∴第次的横坐标为,第次的横坐标也为;
∴第2023次的横坐标为;
第二次和第三次的纵坐标都是1,
第四次和第五次的纵坐标都是,
第六次和第七次的纵坐标都是2,
第八次和第九次的纵坐标都是,
∴从第二次开始纵坐标依次为1,1,,,2,2,,,3,,…
∵第四次和第五次的纵坐标都是,第八次和第九次的纵坐标都是,
∴第次和第次纵坐标的为,
∴第2020次和第2021次的纵坐标都是,
则第2023次的纵坐标是.
∴经过第2023次,点P的坐标是.
故选:C.]
13.[提示:如图所示,根据题意可得,点C的坐标表示为.
故答案为:.]
14.或[提示:由题意,得:或,
解得:或;
故答案为:或.]
15.[提示:∵点向上平移3个单位,
∴点向上平移3个单位,
∵点在x轴上,
∴,解得:,
故答案为:.]
16.[提示:∵,,线段最小,
∴,
故答案为:.]
17.[提示:因为,所以建立如图直角坐标系:
所以点C的坐标为.
故答案为:.]
18.[提示:∵长方形中,,,点坐标为,
∴点D的坐标是,即,
∵点B坐标为,沿某一方向平移后点的坐标为,
∴点B是向左平移3个单位,向上平移4个单位得到点,
∵点的平移规律和点B的平移规律相同,
∴点的坐标是,即点的坐标是.
故答案为:.]
19.或,或[提示:当点在轴上时,
解得:
所以点有两个,,
当点在轴上时,
点符合题意,当点向上移动时,面积变大,
在正半轴不存在符合条件的点.
设在轴负半轴上点,
则
即:
解得:
所以,点坐标为
故答案为:或或]
20.[提示:根据点的运动方式可知,
点的坐标为;
点的坐标为;
点的坐标为;
点的坐标为;
点的坐标为;
点的坐标为;
点的坐标为;
点的坐标为;
点的坐标为;
,
由此可见,点的横坐标为,纵坐标为,
当时,
,
,
所以点的坐标为,
所以点的坐标为,
故答案为:.]
21.(1)(2,4) (5,1)
(2)(3)如图所示
22.解:(1)如图:
(2)给机器人的指令是(3,20°).
23.(1)解:如图所示:即为所求,
(2)的面积为:
24.(1)解:由题意知,a,b满足,
∵,
∴,
∴,
∴;
(2)解:存在,理由如下:
①当P在上运动时,,
∵,
∴,
∴,
∴,
∴,
∴点P的坐标为;
②当P在上运动时,,
∴,
∴,
∴,
∴点P的坐标为,
综上可知,点P的坐标为或.
25.(1)解:∵将三角形沿x轴负方向平移,平移后的图形为三角形,
点B在y轴上,点C的坐标为,
∴三角形沿x轴负方向平移个单位得到三角形,
∵点是由点平移得到的,
∴;
故答案为:
(2)①由(1)可知:,
∵,,
∴,
当时,点P在线段上,,
点P的坐标为.
当时,点P在线段上,,,
∴,
∴点P的坐标为.
②如图,设交于点,
由平移可知:,
∴,
∵,
∴,
∴,
∴,
∴.
26.(1)解:∵,,,
∴,,
∴点,点;
(2)解:∵将线段先向上平移4个单位,再向右平移1个单位后得到线段,,点,
∴点,点,,,
∴,,
∴四边形的面积,
∵四边形的面积等于,
∴点M在点C下方,
∴四边形的面积四边形的面积,
∴;
(3)解:的值不会变化,
理由:如图1,当点N在线段上时,
∵,
∴;
如图2,当点N在x轴的负半轴时,
∵,
∴,
综上所述:是定值8.
27.(1)解:
将点A,B分别向下平移4个单位,向左平移1个单位
故答案为:,四边形的面积为20;
(2)由(1)中、,可得;
如下图所示,过点作
,不发生变化;
(3)如下图所示,过作交于点F,设点
即
解得:,;
故答案为:.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版七下第七章平面直角坐标系单元测试卷
时间100分钟 满分120分
一、选择题(每小题3分,共36分)
1.第19届亚运会2023年9月在浙江省杭州市举行.以下能够准确表示杭州市地理位置的是( )
A.距离兴化市370公 B.在浙江省 C.在兴化市的南方 D.东经,北纬
2.在数轴上,用有序数对表示点的平移,若得到的数为1,得到的数为3,则得到的数为( ).
A.8 B. C.2 D.
3.点的坐标满足,那么点在( )
A.纵轴上 B.横轴上
C.原点 D.纵轴或横轴上
4.已知点在轴上,则的值为( )
A. B.3 C.0 D.
5.已知点 P 在第四象限,且到 x 轴的距离为 3,到 y 轴的距离为 2,则点 P 的坐标是( )
A. B. C. D.
6.若点的坐标是,且平行于轴,则点的坐标为( )
A. B.或
C. D.或
7.象棋起源于中国,中国象棋文化历史悠久.如图,是中国象棋棋盘的一部分,若“帅”位于点,“炮”位于点上,则“兵”位于点( )上.
A. B. C. D.
8.小明从学校出发,步行去少年宫(如图),行走路线正确的是( )
A.向南偏东行走600米 B.向南偏西行走600米
C.向南偏东行走600米 D.向南偏西行走600米
9.在平面直角坐标系中,将点向左平移3个单位,再向下平移1个单位得到,则点的坐标为( )
A. B. C. D.
10.在平面直角坐标系中,已知,将线段平移后得到线段,点A、B的对应点分别是点、. 若点的坐标为,则点的坐标为( ).
A. B. C. D.
11.如图,三角形ABC沿着BC所在直线向右平移a个单位长度得到三角形DEF(点E在点C的左侧).下列判断正确的是( )
结论Ⅰ:若BF=8,EC=4,则a的值为2;
结论Ⅱ:连接AD,若三角形ABC的周长为18,四边形ABFD的周长为22,则a的值为4.
A.Ⅰ和Ⅱ都对 B.Ⅰ和Ⅱ都不对 C.Ⅰ不对Ⅱ对 D.Ⅰ对Ⅱ不对
12.如图,在平面直角坐标系中,动点按箭头所示的方向做折线运动,第一次从原点运动到,第二次从运动到,第三次从运动到,第四次从运动到,第五次从运动到,第六次从运动到……,按这样的运动规律(向右始终保持运动一个单位长度,向上或向下比前一次的向下或向上都多运动一个单位长度),经过第2023次,点的坐标是( )
A. B. C. D.
二、填空题(每小题3分,共24分)
13.如图,雷达探测器在一次探测中发现了三个目标A、B、C,点A、B的坐标分别表示为,则点C的坐标表示为 .
14.已知点到两坐标轴的距离相等,则 .
15.若点向上平移3个单位后得到的点在x轴上,则m的值为 .
16.平面直角坐标系中,已知点,,当线段有最小值时, .
17.如图是轰炸机机群的一个飞行队形,若轰炸机A、B的坐标分别是,则轰炸机C的坐标为 .
18.如图,在平面直角坐标系中,长方形的边与轴平行且,,点坐标为,沿某一方向平移后,点的对应点的坐标为,则点的坐标为 .
19.已知点,点,点是坐标轴上一动点,若三角形的面积为,则的坐标为 .
20.如图,在平面直角坐标系中,设一动点自处向下运动1个单位长度至处,然后向左运动2个单位长度至处,再向上运动2个单位长度至处,再向左运动2个单位长度至处,再向下运动2个单位长度至处,,如此继续运动下去,设,,2,3,,则的坐标是 .
三、解答题(共60分)
21.(8分)下图是游乐园一角的平面示意图,图中1个单位长度表示100m.
(1)如果用有序数对(3,2)表示跳跳床的位置,填写下列两个游乐设施的位置:跷跷板________,碰碰车________;
(2)秋千的位置是(4,5),请在图中标出来;
(3)旋转木马在大门以东500m,再往北200m处,请在图中标出来.
22.(8分)根据指令(s,A)(说明:s≥0,单位:厘米;0°≤A<180°),机器人在平面上能完成下列动作:先原地逆时针旋转角度A,再朝其面对的方向沿直线行走距离s,若机器人站在点M处,面对的方向如图所示.
(1)给机器人下了一个指令(2,60°),机器人移动到了B点,请你画出机器人从M点到B点的运动路径;
(2)若机器人从M点运动到了C点,则给机器人下了一个什么指令?
23.(8分)在平面直角坐标系中,三点的坐标分别为.
(1)在平面直角坐标系中描出各点,并画出.
(2)求的面积.
24.(9分)如图,在平面直角坐标系中,点A,B坐标分别为,,点C在y轴上,且轴,a,b满足.一动点P从原点出发,以每秒2个单位长度的速度沿着的路线运动(点P首次回到点O时停止),运动时间为t秒.
(1)直接写出点A,B的坐标;
(2)点P在运动过程中,是否存在点P到x轴的距离为个单位长度的情况,若存在,求出点P的坐标,若不存在,请说明理由.
25.(9分)如图,点A的坐标为,点B在y轴上,将三角形沿x轴负方向平移,平移后的图形为三角形,且点C的坐标为.
(1)点D的坐标为__________;
(2)在四边形中,点P从点B出发,沿移动,若点P的速度为1个单位长度/秒,运动时间为t秒,回答下列问题:
①求点P在运动过程中的坐标(用含t的式子表示,写出过程);
②当点P运动到时,若,请直接写出的度数.
26.(9分)如图,已知点,满足.将线段先向上平移4个单位,再向右平移1个单位后得到线段,连接,.
(1)直接写出点A和点B的坐标;
(2)点M从O点出发,以每秒1个单位的速度向上平移运动.设运动时间为t秒,当t为多少时,四边形的面积等于?
(3)在(2)的条件下,点M从O点出发的同时,点N从B点出发,以每秒个单位的速度向左平移运动,设射线交y轴于点E.在运动过程中的值是否会发生变化?若不变,请求出它的值;若变化,请说明理由.
27.(9分)如图,在平面直角坐标系中,A,B坐标分别为、,且a,b满足:,现同时将点A,B分别向下平移4个单位,再向左平移1个单位,分别得到点A,B的对应点C,D,连接.
(1)求C,D两点的坐标及四边形的面积;
(2)点P是线段上的一个动点,连接,当点P在上移动时(不与B,D重合),的值是否发生变化,并说明理由;
(3)已知点M在y轴上,且点D在的外部,连接,若的面积与四边形的面积相等,求点M的坐标.
第七章单元测试卷参考答案
1.D[提示:由题意可知,东经,北纬能够准确表示杭州市地理位置,其他都不能准确表示杭州市地理位置.故选:D.]
2.B[提示: 用有序数对表示点的平移,得到的数为1,得到的数为3,
数轴上的数向左边平移个单位得到的数为
数轴上的数向右边平移个单位得到的数为
可表示数轴上的数向左边平移个单位得到的数是
故选:]
3.C[提示:由,得
,,
∴点在原点.
故选:C.]
4.B[提示:点在轴上,
,解得.
故选:B.]
5.D[提示:点在第四象限,且到轴的距离为3,到轴的距离为2,
点的横坐标是2,纵坐标是,
点的坐标是.
故选:D]
6.D[提示:已知点,轴,且,则点的坐标为或,
故选:D]
7.A[提示:∵“兵”在“炮”的上面,
∴“兵”的纵坐标是,
∵“兵”在“帅”的左面第一格上,
∴“兵”的横坐标是,
∴“兵”的坐标是,
故选:.]
8.B[提示:小明从学校出发,步行去少年宫行走路线是:向南偏西行走米.
故选:B.]
9.C[提示:∵向左平移3个单位长度后,再向下平移1个单位长度,
∴,,
∴点的坐标为,
故选:C.]
10.B[提示:∵,,
∴点向右平移4个单位,向下平移3个单位得点,
∴点向右平移4个单位,向下平移3个单位得点.
故选:B.]
11.D[提示:∵三角形ABC沿着BC所在直线向右平移a个单位长度得到三角形DEF,
∴BE=CF=a,
∵BF=BE+CE+CF,BF=8,EC=4,
∴8=a+4+a,
∴a=2,故结论Ⅰ正确;
∵三角形ABC沿着BC所在直线向右平移a个单位长度得到三角形DEF,
∴AC=DF,
∵四边形ABFD的周长为22,
∴AB+BC+CF+DF+AD=22,
∴AB+BC+CF+AC+AD=22,
∵三角形ABC的周长为18,
∴AB+BC+AC=18,
∴18+CF+AD=22,即18+a+a=22,
∴a=2,故结论(Ⅱ)不正确,
∴Ⅰ对Ⅱ不对,
故选:D.]
12.C[提示:根据题意可得,
第一次从原点运动到,
第二次从运动到,
第三次从运动到,
第四次从运动到,
第五次从运动到,
第六次从运动到,
第七次从运动到,
第八次从运动到,
第九次从运动到,
…
∴第一次和第二次的横坐标都为1,
第三次和第四次的横坐标都为2,
第五次和第六次的横坐标都为3,
∴第次的横坐标为,第次的横坐标也为;
∴第2023次的横坐标为;
第二次和第三次的纵坐标都是1,
第四次和第五次的纵坐标都是,
第六次和第七次的纵坐标都是2,
第八次和第九次的纵坐标都是,
∴从第二次开始纵坐标依次为1,1,,,2,2,,,3,,…
∵第四次和第五次的纵坐标都是,第八次和第九次的纵坐标都是,
∴第次和第次纵坐标的为,
∴第2020次和第2021次的纵坐标都是,
则第2023次的纵坐标是.
∴经过第2023次,点P的坐标是.
故选:C.]
13.[提示:如图所示,根据题意可得,点C的坐标表示为.
故答案为:.]
14.或[提示:由题意,得:或,
解得:或;
故答案为:或.]
15.[提示:∵点向上平移3个单位,
∴点向上平移3个单位,
∵点在x轴上,
∴,解得:,
故答案为:.]
16.[提示:∵,,线段最小,
∴,
故答案为:.]
17.[提示:因为,所以建立如图直角坐标系:
所以点C的坐标为.
故答案为:.]
18.[提示:∵长方形中,,,点坐标为,
∴点D的坐标是,即,
∵点B坐标为,沿某一方向平移后点的坐标为,
∴点B是向左平移3个单位,向上平移4个单位得到点,
∵点的平移规律和点B的平移规律相同,
∴点的坐标是,即点的坐标是.
故答案为:.]
19.或,或[提示:当点在轴上时,
解得:
所以点有两个,,
当点在轴上时,
点符合题意,当点向上移动时,面积变大,
在正半轴不存在符合条件的点.
设在轴负半轴上点,
则
即:
解得:
所以,点坐标为
故答案为:或或]
20.[提示:根据点的运动方式可知,
点的坐标为;
点的坐标为;
点的坐标为;
点的坐标为;
点的坐标为;
点的坐标为;
点的坐标为;
点的坐标为;
点的坐标为;
,
由此可见,点的横坐标为,纵坐标为,
当时,
,
,
所以点的坐标为,
所以点的坐标为,
故答案为:.]
21.(1)(2,4) (5,1)
(2)(3)如图所示
22.解:(1)如图:
(2)给机器人的指令是(3,20°).
23.(1)解:如图所示:即为所求,
(2)的面积为:
24.(1)解:由题意知,a,b满足,
∵,
∴,
∴,
∴;
(2)解:存在,理由如下:
①当P在上运动时,,
∵,
∴,
∴,
∴,
∴,
∴点P的坐标为;
②当P在上运动时,,
∴,
∴,
∴,
∴点P的坐标为,
综上可知,点P的坐标为或.
25.(1)解:∵将三角形沿x轴负方向平移,平移后的图形为三角形,
点B在y轴上,点C的坐标为,
∴三角形沿x轴负方向平移个单位得到三角形,
∵点是由点平移得到的,
∴;
故答案为:
(2)①由(1)可知:,
∵,,
∴,
当时,点P在线段上,,
点P的坐标为.
当时,点P在线段上,,,
∴,
∴点P的坐标为.
②如图,设交于点,
由平移可知:,
∴,
∵,
∴,
∴,
∴,
∴.
26.(1)解:∵,,,
∴,,
∴点,点;
(2)解:∵将线段先向上平移4个单位,再向右平移1个单位后得到线段,,点,
∴点,点,,,
∴,,
∴四边形的面积,
∵四边形的面积等于,
∴点M在点C下方,
∴四边形的面积四边形的面积,
∴;
(3)解:的值不会变化,
理由:如图1,当点N在线段上时,
∵,
∴;
如图2,当点N在x轴的负半轴时,
∵,
∴,
综上所述:是定值8.
27.(1)解:
将点A,B分别向下平移4个单位,向左平移1个单位
故答案为:,四边形的面积为20;
(2)由(1)中、,可得;
如下图所示,过点作
,不发生变化;
(3)如下图所示,过作交于点F,设点
即
解得:,;
故答案为:.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
