第七章 平面直角坐标系素养提优卷(含解析)
文档属性
| 名称 | 第七章 平面直角坐标系素养提优卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-22 17:11:11 | ||
图片预览




文档简介
第七章 平面直角坐标系 素养提优卷
考试分数:120分 考试时间:100分钟
一、单选题(本大题共10小题,共30分)
1.已知点,若直线与x轴平行,则N点坐标可能是( )
A. B. C. D.
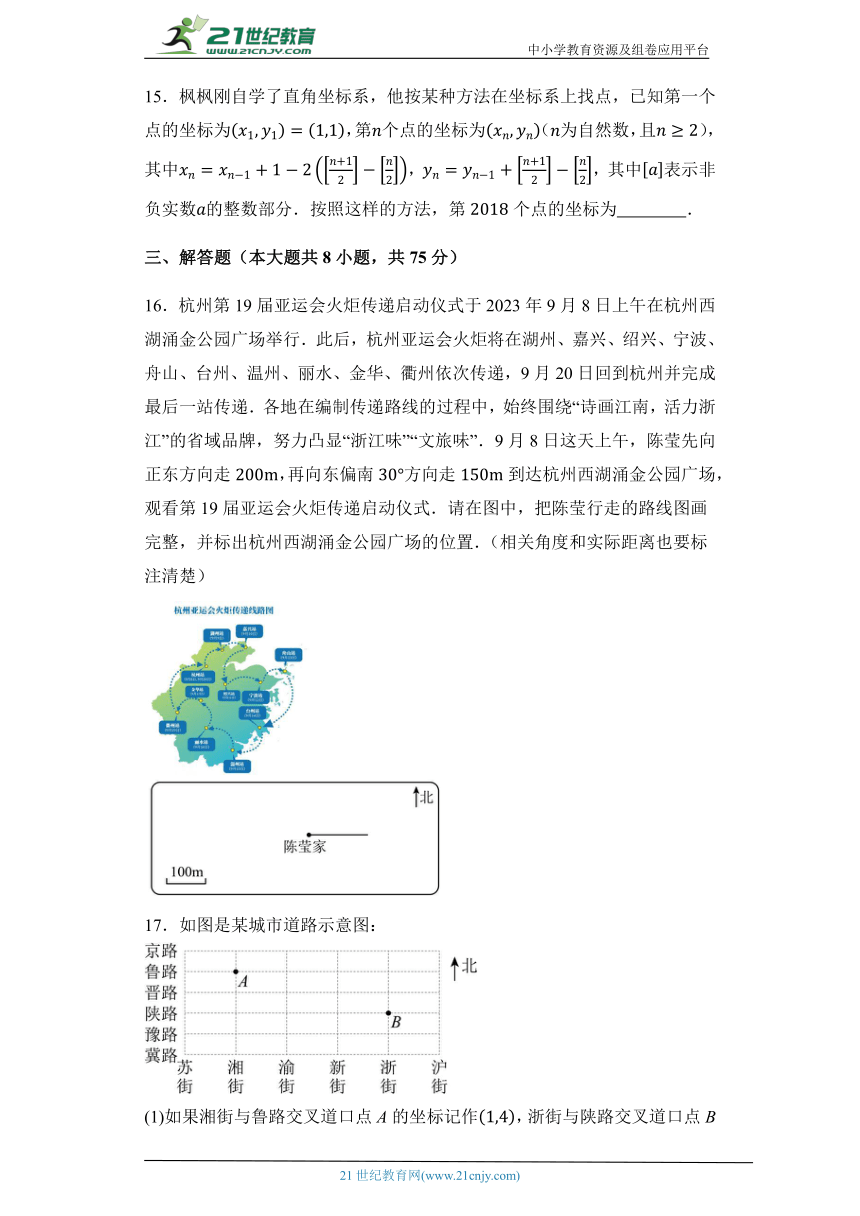
2.如图,点M,N,P,Q在平面直角坐标系中,若过点的直线与x轴垂直,则直线会经过( )
A.点M B.点N C.点P D.点Q
第2题图 第4题图 第5题图
3.在平面直角坐标系中,点在坐标轴上,下列判断正确的是( )
甲:t可能是3 乙:可能是5 丙:点A距离原点2个单位长度
A.甲和丙 B.乙和丙 C.甲和乙 D.甲、乙、丙
4.如图,点在线段上,则点的纵坐标可能是( )
A. B.4 C.6 D.
5.端午节期间,小强批发了甲、乙、丙、丁四种不同品牌的雪糕,每种品牌雪糕的数量和总价如图所示,其中单价最贵的品牌是( )
A.甲 B.乙 C.丙 D.丁
6.一个平面直角坐标系的横轴和纵轴的单位长度相同,该平面直角坐标系中的点,的位置如图所示,则该平面直角坐标系的原点可能是( )
A.点A B.点B C.点C D.点D
7.如图,长方形ABCD位于第一象限,AB 轴,AD 轴.已知P(,)是长方形ABCD(含边界)内的一个动点,A、C的坐标如图所示,则的最大值与最小值分别是( )
A.4, B.3, C.4, D.3,
第6题图 第7题图 第8题图
8.风力发电是一种常见的绿色环保发电形式,它能够使大自然的资源得到更好地利用.如图1,风力发电机有三个底端重合、两两成角的叶片,以三个叶片的重合点为原点,水平方向为轴建立平面直角坐标系(如图2所示),已知开始时其中一个叶片的外端点的坐标为,在一段时间内,叶片每秒绕原点顺时针转动,则第时,点的对应点的坐标为( )
A. B. C. D.
9.数学家高斯推动了数学科学的发展,被数学界誉为“数学王子”,据传,他在计算时,用到了一种方法,将首尾两个数相加,进而得到.人们借助于这样的方法,得到(n是正整数).有下列问题,如图,在平面直角坐标系中的一系列格点,其中,且是整数.记,如,即,即,即,以此类推.则下列结论正确的是( )
A. B. C. D.
第9题图 第10题图
10.中国结是一种手工编织工艺品,因为其外观对称精致,可以代表汉族悠久的历史,符合中国传统装饰的习俗和审美观念,故命名为中国结,中国结的意义在于它所显示的情致与智慧正是汉族古老文明中的一个侧面,也是数学奥秘的游戏呈现.它有着复杂曼妙的曲线,却可以还原成最单纯的二维线条,其中的八字结对应着数学曲线中的双扭线在平面直角坐标系中如图所示,则下列结论中正确的有( )
①双扭线围成的面积小于6;
②双扭线内部(包含边界)包含11个整数点(横坐标、纵坐标都是整数的点);
③双扭线上任意一点到原点的距离不超过3;
④假设点为双扭线上的一个点,,为双扭线与轴的交点(如图所示),则满足的点有4个.
A.①②③ B.②③ C.②③④ D.①②③④
二、填空题(本大题共5小题,共15分)
11.若西经,南纬用有序数对,来表示,东经,北纬用有序实数对,来表示,则有序实数对,的含义是 .
12.点(a≥0)所在的象限是 .
13.某中学参加运动会开幕式表演,为了使表演方队整齐有序,需要在操场上标记若干个关键点,如图是几个关键点的位置,若建立平面直角坐标系,点A的坐标为,点B的坐标为,则点C的坐标为 .
第13题图 第14题图
14.如下图是一组密码的一部分,聪明的小锋通过“今天考试”的译文是“努力发挥”找到了密码钥匙是:对应文字横坐标加1,纵坐标加2,则“正做数学”的译文是 .
15.枫枫刚自学了直角坐标系,他按某种方法在坐标系上找点,已知第一个点的坐标为,第个点的坐标为(为自然数,且),其中,,其中表示非负实数的整数部分.按照这样的方法,第个点的坐标为 .
三、解答题(本大题共8小题,共75分)
16.杭州第19届亚运会火炬传递启动仪式于2023年9月8日上午在杭州西湖涌金公园广场举行.此后,杭州亚运会火炬将在湖州、嘉兴、绍兴、宁波、舟山、台州、温州、丽水、金华、衢州依次传递,9月20日回到杭州并完成最后一站传递.各地在编制传递路线的过程中,始终围绕“诗画江南,活力浙江”的省域品牌,努力凸显“浙江味”“文旅味”.9月8日这天上午,陈莹先向正东方向走,再向东偏南方向走到达杭州西湖涌金公园广场,观看第19届亚运会火炬传递启动仪式.请在图中,把陈莹行走的路线图画完整,并标出杭州西湖涌金公园广场的位置.(相关角度和实际距离也要标注清楚)
17.如图是某城市道路示意图:
(1)如果湘街与鲁路交叉道口点A的坐标记作,浙街与陕路交叉道口点B的坐标记作,则此时是______街与______路的交叉道口;
(2)在(1)的条件下渝街与陕路交叉道口的坐标记作______;沪街与京路交叉道口的坐标记作______;
(3)用有序数对写出2种从A地到B地的最短路线,如:
—————.
18.如图,在平面直角坐标系中,,,若点C在y轴右侧,轴且.
(1)求点C的坐标;
(2)在图中画出,并求的面积:
(3)若点P在x轴上运动,连接AP,当线段AP长度最小时,点P的坐标为_____依据是_______.
19.如图是由边长为1的小正方形构成的的正方形网格,每个小正方形的顶点叫格点.建立如图所示的平面直角坐标系,若,,.
(1)若,直接写出所有满足条件的格点D的坐标 .
(2)在(1)的条件下,若,请在上找一点M,使得(不写画法,保留作图痕迹),并请写出点M的坐标 .
20.在如图所示的平面直角坐标系中,为坐标原点,点,且点在轴上;点;解答下列各题:
(1)点A的坐标为 ;
(2)点在轴上,且轴,则点的坐标为 ;
(3)连接、、,如果把三角形各个顶点纵坐标保持不变,横坐标都减去,得到三角形.
①请画出三角形;
②连接、,那么与的关系是 ;
③请直接写出四边形的面积.
21.如图,四边形是长方形,边在轴上,轴. 已知点坐标为,点坐标为. 动点从点出发,以每秒个单位长度的速度沿折线向终点运动,设点的运动时间为.
(1)点坐标为 ;
(2)连接,当直线将长方形的面积分为的两部分时,求的值;
(3)连接,,直接写出三角形的面积为3时,点的坐标.
22.如图1,,,我们能够容易地计算出的面积,根据所给的平面直角坐标系探究下列问题.(说明:三角形记作)
【思维启迪】.
(1)若点的坐标是,点的坐标是,则
①的面积是______,的面积是______;
②的面积与的面积之间的数量关系是______;
③三点所在的直线与x轴的位置关系是______.
请利用你发现的结论,尝试解决以下问题.
【学以致用】
(2)是轴上方一点,点的坐标是,若的面积与的面积相等,且,求点的坐标.
【发散思维】
(3)如图2,若点的坐标是,连接,点在轴上,线段与线段相交于点,若的面积与的面积相等,请直接写出点的坐标.
23.如图1,在平面直角坐标系中,已知,将线段沿x轴正方向平移至,,且,连接.
(1)写出点A的坐标为_______;点B的坐标为_______;
(2)连接,在y轴上是否存在一点P,使三角形的面积等于三角形的面积?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)点D为的中点,点E是线段上一动点(点E不与点D、C重合),连接、.
①如图2,若,,求的度数;
②如图3,已知,,与相交于点F,点F在下方,若,.在点E运动的过程中,的值是否发生改变?若不变,请求出的值?若改变,请说明理由.
中小学教育资源及组卷应用平台
试卷第1页,共3页
21世纪教育网(www.21cnjy.com)
参考答案:
1.D
【分析】根据直线与x轴平行,得到点M、N的纵坐标相等可得答案.
【详解】解:∵直线与x轴平行,
∴点M、N的纵坐标相等,
∵,
∴点N的纵坐标为4,
故选:D.
【点睛】本题考查坐标与图形,熟知与坐标轴平行的点的坐标特征是解答的关键.
2.A
【分析】根据点在第三象限,即可判断.
【详解】解:∵点在第三象限,且过点的直线与x轴垂直,
∴直线会经过点M,
故选:A.
【点睛】本题考查了点的坐标,解题的关键是明确题意,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限;第二象限;第三象限;第四象限.
3.D
【分析】分点A在x轴和y轴上两种情况,求出t值,得到点A坐标,从而判断出距离原点的长度,即可判断.
【详解】解:若点在x轴上,
则,
则,
此时,距离原点2个单位长度;
若点在y轴上,
则,
则,
此时,距离原点2个单位长度;
∴甲、乙、丙的说法都正确,
故选D.
【点睛】本题考查了坐标与图形,解题的关键是分点在x轴和y轴两种情况进行讨论,难度不大.
4.B
【分析】观察图象可知,点的纵坐标在和之间,即可得出答案.
【详解】解:观察图象可知,点的纵坐标在和之间,
点的纵坐标可能是,
故选:B.
【点睛】本题考查了坐标与图形性质,考查数形结合思想,观察图象得到点的纵坐标在和之间是解题关键.
5.B
【分析】根据图象中的数据,结合单价总价数量,分别求出每种品牌雪糕的单价,即可得到答案.
【详解】解:由图象可知,甲品牌雪糕的单价为:元/根,
乙品牌雪糕的单价为:元/根,
丙品牌雪糕的单价为:元/根,
丁品牌雪糕的单价为:元/根,
,
乙品牌雪糕的单价最贵,
故选:B.
【点睛】本题考查了坐标和图形,有理数的除法,有理数的大小比较,根据已知图象获取正确信息是解题关键.
6.A
【分析】根据题意和坐标与图形可确定原点可能位置.
【详解】解:由和知,M、N都位于第一象限,且N到x轴的距离为M到x轴的距离的2倍,N到y轴的距离为M到x轴的距离的5倍,
又平面直角坐标系的横轴和纵轴的单位长度相同,
∴则该平面直角坐标系的原点可能是点A,
故选:A.
【点睛】本题考查点的坐标、坐标与图形,理解题意,正确得到原点可能位置是解答的关键.
7.B
【分析】根据题意,结合坐标系中a,b的最值,分析得出的最大值与最小值即可
【详解】解:根据题意,当取最大值时,即a最小,b最大,则,
∴的最大值是3,
当取最小值时,即a最大,b最小,则,
∴的最小值是.
故选:B.
【点睛】此题考查了坐标与图形的性质,解题关键是根据题意找出a,b的最值.
8.B
【分析】根据旋转的性质分别求出第1、2、3、4s时,点A的对应点、、、的坐标,找到规律,进而得出第时,点A的对应点的坐标.
【详解】解:∵,
∴A在第一象限的角平分线上,
∵叶片每秒绕原点顺时针转动,
∴,,,,
∴点A的坐标以每4秒为一个周期依次循环,
∵,
∴第时,点A的对应点的坐标与相同,为.
故选:B.
【点睛】本题考查了旋转的性质,点的坐标,找到点A的坐标循环的规律是解题的关键.
9.B
【分析】利用图形寻找规律,再利用规律解题即可.
【详解】解:第1圈有1个点,即,这时;
第2圈有8个点,即到;
第3圈有16个点,即到,;
依次类推,第n圈,;
由规律可知:是在第23圈上,且,则即,故A选项不正确;
是在第23圈上,且,即,故B选项正确;
第n圈,,所以,故C、D选项不正确;
故选B.
【点睛】本题考查图形与规律,利用所给的图形找到规律是解题的关键.
10.C
【分析】由题得,点A、B、P、Q、M、N都在双扭线上,计算的面积,观察图形,即可判断各个结论.
【详解】解:如图,连接,
得,,
∴双扭线围成的面积大于6,故①不正确;
由图得,双扭线内部包含4个整数点,
边界上有7个整数点,
共11个,故②正确;
由图得,点A、B与原点距离最大为3,故③正确;
设的高为h,
∵,且,
∴,
由图得,点P、Q、M、N均满足题意,故④正确,
故选:C.
【点睛】本题考查了在坐标系中判断点的位置,合理的推断及计算是解题关键.
11.东经,南纬
【分析】根据题意可得第一个数是经度,西为正,东为负,第二个数为纬度,南为正,北为负,据此,即可求解.
【详解】解:依题意,有序实数对,的含义是东经,南纬
故答案为:东经,南纬.
【点睛】本题考查了有序实数对表示位置,正负数的意义,理解题意是解题的关键.
12.第二象限
【解析】略
13.
【分析】先根据点A和点B的坐标建立平面直角坐标系,然后写出点C的坐标.
【详解】如图,
∴点C的坐标为.
故答案为:.
【点睛】本题考查了用坐标表示位置,正确建立平面直角坐标系是解答本题的关键.
14.祝你成功
【分析】先确定原文坐标,再根据密码钥匙,转化为译文即可.
【详解】设每个正方形的边长是一个单位长度,
∵正的坐标为,做的坐标为,数的坐标为,学的坐标为,
∴译文坐标分别是,,, ,译文为祝你成功,
故答案为:祝你成功.
【点睛】本题考查了坐标表示位置,熟练掌握坐标与位置的关系是解题的关键.
15.
【分析】本题考查了坐标位置的确定,根据题目条件找出横坐标和纵坐标的规律是解题的关键,规律性强,难度较大,根据规律性找出横坐标和纵坐标的规律公式,然后把代入进行计算即可求解.
【详解】解:当n为偶数时,;
当n为奇数时,.
∴依次为1,2,1,2,…;依次为1,1,2,2,3,3,….
∴,
∴第个点的坐标为.
16.见解析
【分析】本题考查作图-应用与涉及作图,根据题意画出图形即可.
【详解】解:如图:
17.(1)苏,冀
(2),
(3)见解析
【分析】(1)根据点A和点B的坐标,即可找到的位置;
(2)参照的位置,可得其他交叉道口的坐标;
(3)答案不唯一,要求路程总长最短即可.
【详解】(1)解:此时是苏街与冀路的交叉道口,
故答案为:苏,冀;
(2)以苏街与冀路的交叉道口为,
则渝街与陕路交叉道口的坐标记作,
沪街与京路交叉道口的坐标记作,
故答案为:,;
(3)最短路线可以为:—————,
或—————.
【点睛】本题考查了确定位置,解题的关键是用已知点的位置做参照,找到其他位置.
18.(1)
(2)见解析,的面积6
(3)见详解
【分析】(1)因为轴,点C与点纵坐标相等,点C在y轴右侧,且,即可求出横坐标;
(2)利用三角形面积求解即可;
(3)利用“垂线段最短”,解答即可.
【详解】(1)解:轴,,点C在y轴右侧,且.
∴点C的坐标为:;
故答案为:;
(2)如图:
的面积:
(3)
当线段AP长度最小时,点P的坐标为,依据是直线外一点与直线上各点连线中垂线段最短.
【点睛】本题考查了作图-复杂作图,坐标与图形性质,解答本题的关键是准确作图.
19.(1)或
(2)见解析,;()
【分析】(1)平移,使点与点重合,然后确定和点坐标即可;
(2)利用矩形的对角线互相平分得到点,作图写出坐标即可.
【详解】(1)解:如图,
(2)如图,
点M为所作,M点的坐标为()
故答案为:;().
【点睛】本题考查了作图,基本作图,坐标与图形性质,熟练结合以上知识准确作图并写出坐标是解题的关键.
20.(1)
(2)
(3)①详见解析;②平行且相等;(,)③
【分析】(1)根据轴上的点的横坐标为0,进而得出,代入点坐标,即可求解;
(2)根据点在轴上,轴,且点,求得点的坐标;
(3)①根据的坐标,将横坐标都减去2,得到,顺次连接得到三角形;
②根据平移的性质可得,;
③根据坐标以及平行四边形的面积公式即可求解.
【详解】(1)解:∵点,且点在轴上;
∴,解得:,
∴
∴;
故答案为:;
(2)解:∵轴,且点,
∴的横坐标为,
又点在轴上,
∴,
∴故答案为:;
(3)①如图,三角形即为所求;
②根据平移的性质可得,
故答案为:平行且相等;(,).
③四边形面积为4.
【点睛】本题考查了坐标与图形,平移作图,平移的性质,熟练掌握以上知识是解题的关键.
21.(1)
(2)或;
(3)满足条件的点的坐标为或.
【分析】(1)利用矩形的性质求出,,可得结论;
(2)分两种情形:如图1中,当点在线段上时,如图2中,当点在线段上时,分别构建方程求解;
(3)当点与重合时,的面积为3,此时,过点作交于点,此时,的面积为3,求出坐标即可.
【详解】(1)解:四边形是矩形,,,
,,
,
故答案为:;
(2)解:如图1中,当点在线段上时,
由题意,,
,
.
如图2中,当点在线段上时,
由题意,,
,
.
综上所述,满足条件的的值为或;
(3)解:如图3中,
当点与重合时,的面积为3,此时,
过点作交于点,此时,的面积为3,
,
综上所述,满足条件的点的坐标为或.
【点睛】本题属于四边形综合题,考查了矩形的性质,三角形的面积等知识,解题的关键是学会用分类讨论的思想思考问题,学会利用参数构建方程解决问题.
22.(1)①,②相等,③平行;(2)点的坐标是或;(3)
【分析】(1)①根据点的坐标是,点的坐标是,,可知,,进而即可解答;②点的坐标是,点的坐标是,,可知,,,进而即可解答;③根据点的坐标是,点的坐标是,横坐标相等即可解答;
(2)根据设点,根据面积相等,再根据可知进而即可解答;
(3)根据可知进而即可解答.
【详解】解:(1)①∵点的坐标是,点的坐标是,,,
∴ ,,,
∴,,
故答案为;
②∵点的坐标是,点的坐标是,,
∴,,,,
∴,
∴,
∴,
故答案为;
③∵点的坐标是,点的坐标是,,
∴三点的横坐标相等,
∴三点所在的直线与x轴的位置关系是平行.
(2)∵设点,在平面直角坐标系内取一点,连接,
过点作轴的垂线交轴于,过点作轴的垂线交轴于点,
∵,
∴,
∴,
∵,
∴,
∴,
∴,
∵点在轴上方,
∴,
∵,,,,
∴,
∴,
∴,
∴或,
(3)设,
∵点的坐标是,点的坐标是,, ,点的坐标是,
∴,,,,,,
∵,
∴,
∴,
∴,
∴,
∴,
∴,
∵不符合题意,
∴,
∴点.
【点睛】本题考查了平面直角坐标系内点的坐标特征,平行于轴的点的坐标特征,三角形的面积与平面直角坐标系,掌握平面直角坐标系内点的坐标特征是解题的关键.
23.(1),
(2)存在,或
(3)①,②不变,3
【分析】(1)非负性求出的值,进而得到点坐标,再根据平移的性质,求出点的坐标即可;
(2)设点,根据三角形的面积等于三角形的面积,列出方程求解即可;
(3)①过点作,平移得到,进而得到,根据平行线的性质,推出,即可;
②设交于点,由①可知:,根据给定的角度之间的关系,结合三角形的内角和定理,求出,进一步得出结果即可.
【详解】(1)解:∵,
∴,
∴,
∴,
∵平移后的点的坐标为,
∴,即:;
故答案为:,;
(2)∵,
∴,
设点,
∴,
∴;
∴或;
(3)①过点作,
∵,
∴,
∴,
∴,,
∴;
②不变,设交于点,则:,
∵,,
∴,,
由①知:,
∴,
∴,
∴,
∴,为定值.
【点睛】本题考查非负性,坐标与图形变换—平移,平行线的判定和性质,三角形的内角和定理,熟练掌握平移的性质,求出点的坐标,利用数形结合的思想进行求解,是解题的关键.
答案第1页,共2页
考试分数:120分 考试时间:100分钟
一、单选题(本大题共10小题,共30分)
1.已知点,若直线与x轴平行,则N点坐标可能是( )
A. B. C. D.
2.如图,点M,N,P,Q在平面直角坐标系中,若过点的直线与x轴垂直,则直线会经过( )
A.点M B.点N C.点P D.点Q
第2题图 第4题图 第5题图
3.在平面直角坐标系中,点在坐标轴上,下列判断正确的是( )
甲:t可能是3 乙:可能是5 丙:点A距离原点2个单位长度
A.甲和丙 B.乙和丙 C.甲和乙 D.甲、乙、丙
4.如图,点在线段上,则点的纵坐标可能是( )
A. B.4 C.6 D.
5.端午节期间,小强批发了甲、乙、丙、丁四种不同品牌的雪糕,每种品牌雪糕的数量和总价如图所示,其中单价最贵的品牌是( )
A.甲 B.乙 C.丙 D.丁
6.一个平面直角坐标系的横轴和纵轴的单位长度相同,该平面直角坐标系中的点,的位置如图所示,则该平面直角坐标系的原点可能是( )
A.点A B.点B C.点C D.点D
7.如图,长方形ABCD位于第一象限,AB 轴,AD 轴.已知P(,)是长方形ABCD(含边界)内的一个动点,A、C的坐标如图所示,则的最大值与最小值分别是( )
A.4, B.3, C.4, D.3,
第6题图 第7题图 第8题图
8.风力发电是一种常见的绿色环保发电形式,它能够使大自然的资源得到更好地利用.如图1,风力发电机有三个底端重合、两两成角的叶片,以三个叶片的重合点为原点,水平方向为轴建立平面直角坐标系(如图2所示),已知开始时其中一个叶片的外端点的坐标为,在一段时间内,叶片每秒绕原点顺时针转动,则第时,点的对应点的坐标为( )
A. B. C. D.
9.数学家高斯推动了数学科学的发展,被数学界誉为“数学王子”,据传,他在计算时,用到了一种方法,将首尾两个数相加,进而得到.人们借助于这样的方法,得到(n是正整数).有下列问题,如图,在平面直角坐标系中的一系列格点,其中,且是整数.记,如,即,即,即,以此类推.则下列结论正确的是( )
A. B. C. D.
第9题图 第10题图
10.中国结是一种手工编织工艺品,因为其外观对称精致,可以代表汉族悠久的历史,符合中国传统装饰的习俗和审美观念,故命名为中国结,中国结的意义在于它所显示的情致与智慧正是汉族古老文明中的一个侧面,也是数学奥秘的游戏呈现.它有着复杂曼妙的曲线,却可以还原成最单纯的二维线条,其中的八字结对应着数学曲线中的双扭线在平面直角坐标系中如图所示,则下列结论中正确的有( )
①双扭线围成的面积小于6;
②双扭线内部(包含边界)包含11个整数点(横坐标、纵坐标都是整数的点);
③双扭线上任意一点到原点的距离不超过3;
④假设点为双扭线上的一个点,,为双扭线与轴的交点(如图所示),则满足的点有4个.
A.①②③ B.②③ C.②③④ D.①②③④
二、填空题(本大题共5小题,共15分)
11.若西经,南纬用有序数对,来表示,东经,北纬用有序实数对,来表示,则有序实数对,的含义是 .
12.点(a≥0)所在的象限是 .
13.某中学参加运动会开幕式表演,为了使表演方队整齐有序,需要在操场上标记若干个关键点,如图是几个关键点的位置,若建立平面直角坐标系,点A的坐标为,点B的坐标为,则点C的坐标为 .
第13题图 第14题图
14.如下图是一组密码的一部分,聪明的小锋通过“今天考试”的译文是“努力发挥”找到了密码钥匙是:对应文字横坐标加1,纵坐标加2,则“正做数学”的译文是 .
15.枫枫刚自学了直角坐标系,他按某种方法在坐标系上找点,已知第一个点的坐标为,第个点的坐标为(为自然数,且),其中,,其中表示非负实数的整数部分.按照这样的方法,第个点的坐标为 .
三、解答题(本大题共8小题,共75分)
16.杭州第19届亚运会火炬传递启动仪式于2023年9月8日上午在杭州西湖涌金公园广场举行.此后,杭州亚运会火炬将在湖州、嘉兴、绍兴、宁波、舟山、台州、温州、丽水、金华、衢州依次传递,9月20日回到杭州并完成最后一站传递.各地在编制传递路线的过程中,始终围绕“诗画江南,活力浙江”的省域品牌,努力凸显“浙江味”“文旅味”.9月8日这天上午,陈莹先向正东方向走,再向东偏南方向走到达杭州西湖涌金公园广场,观看第19届亚运会火炬传递启动仪式.请在图中,把陈莹行走的路线图画完整,并标出杭州西湖涌金公园广场的位置.(相关角度和实际距离也要标注清楚)
17.如图是某城市道路示意图:
(1)如果湘街与鲁路交叉道口点A的坐标记作,浙街与陕路交叉道口点B的坐标记作,则此时是______街与______路的交叉道口;
(2)在(1)的条件下渝街与陕路交叉道口的坐标记作______;沪街与京路交叉道口的坐标记作______;
(3)用有序数对写出2种从A地到B地的最短路线,如:
—————.
18.如图,在平面直角坐标系中,,,若点C在y轴右侧,轴且.
(1)求点C的坐标;
(2)在图中画出,并求的面积:
(3)若点P在x轴上运动,连接AP,当线段AP长度最小时,点P的坐标为_____依据是_______.
19.如图是由边长为1的小正方形构成的的正方形网格,每个小正方形的顶点叫格点.建立如图所示的平面直角坐标系,若,,.
(1)若,直接写出所有满足条件的格点D的坐标 .
(2)在(1)的条件下,若,请在上找一点M,使得(不写画法,保留作图痕迹),并请写出点M的坐标 .
20.在如图所示的平面直角坐标系中,为坐标原点,点,且点在轴上;点;解答下列各题:
(1)点A的坐标为 ;
(2)点在轴上,且轴,则点的坐标为 ;
(3)连接、、,如果把三角形各个顶点纵坐标保持不变,横坐标都减去,得到三角形.
①请画出三角形;
②连接、,那么与的关系是 ;
③请直接写出四边形的面积.
21.如图,四边形是长方形,边在轴上,轴. 已知点坐标为,点坐标为. 动点从点出发,以每秒个单位长度的速度沿折线向终点运动,设点的运动时间为.
(1)点坐标为 ;
(2)连接,当直线将长方形的面积分为的两部分时,求的值;
(3)连接,,直接写出三角形的面积为3时,点的坐标.
22.如图1,,,我们能够容易地计算出的面积,根据所给的平面直角坐标系探究下列问题.(说明:三角形记作)
【思维启迪】.
(1)若点的坐标是,点的坐标是,则
①的面积是______,的面积是______;
②的面积与的面积之间的数量关系是______;
③三点所在的直线与x轴的位置关系是______.
请利用你发现的结论,尝试解决以下问题.
【学以致用】
(2)是轴上方一点,点的坐标是,若的面积与的面积相等,且,求点的坐标.
【发散思维】
(3)如图2,若点的坐标是,连接,点在轴上,线段与线段相交于点,若的面积与的面积相等,请直接写出点的坐标.
23.如图1,在平面直角坐标系中,已知,将线段沿x轴正方向平移至,,且,连接.
(1)写出点A的坐标为_______;点B的坐标为_______;
(2)连接,在y轴上是否存在一点P,使三角形的面积等于三角形的面积?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)点D为的中点,点E是线段上一动点(点E不与点D、C重合),连接、.
①如图2,若,,求的度数;
②如图3,已知,,与相交于点F,点F在下方,若,.在点E运动的过程中,的值是否发生改变?若不变,请求出的值?若改变,请说明理由.
中小学教育资源及组卷应用平台
试卷第1页,共3页
21世纪教育网(www.21cnjy.com)
参考答案:
1.D
【分析】根据直线与x轴平行,得到点M、N的纵坐标相等可得答案.
【详解】解:∵直线与x轴平行,
∴点M、N的纵坐标相等,
∵,
∴点N的纵坐标为4,
故选:D.
【点睛】本题考查坐标与图形,熟知与坐标轴平行的点的坐标特征是解答的关键.
2.A
【分析】根据点在第三象限,即可判断.
【详解】解:∵点在第三象限,且过点的直线与x轴垂直,
∴直线会经过点M,
故选:A.
【点睛】本题考查了点的坐标,解题的关键是明确题意,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限;第二象限;第三象限;第四象限.
3.D
【分析】分点A在x轴和y轴上两种情况,求出t值,得到点A坐标,从而判断出距离原点的长度,即可判断.
【详解】解:若点在x轴上,
则,
则,
此时,距离原点2个单位长度;
若点在y轴上,
则,
则,
此时,距离原点2个单位长度;
∴甲、乙、丙的说法都正确,
故选D.
【点睛】本题考查了坐标与图形,解题的关键是分点在x轴和y轴两种情况进行讨论,难度不大.
4.B
【分析】观察图象可知,点的纵坐标在和之间,即可得出答案.
【详解】解:观察图象可知,点的纵坐标在和之间,
点的纵坐标可能是,
故选:B.
【点睛】本题考查了坐标与图形性质,考查数形结合思想,观察图象得到点的纵坐标在和之间是解题关键.
5.B
【分析】根据图象中的数据,结合单价总价数量,分别求出每种品牌雪糕的单价,即可得到答案.
【详解】解:由图象可知,甲品牌雪糕的单价为:元/根,
乙品牌雪糕的单价为:元/根,
丙品牌雪糕的单价为:元/根,
丁品牌雪糕的单价为:元/根,
,
乙品牌雪糕的单价最贵,
故选:B.
【点睛】本题考查了坐标和图形,有理数的除法,有理数的大小比较,根据已知图象获取正确信息是解题关键.
6.A
【分析】根据题意和坐标与图形可确定原点可能位置.
【详解】解:由和知,M、N都位于第一象限,且N到x轴的距离为M到x轴的距离的2倍,N到y轴的距离为M到x轴的距离的5倍,
又平面直角坐标系的横轴和纵轴的单位长度相同,
∴则该平面直角坐标系的原点可能是点A,
故选:A.
【点睛】本题考查点的坐标、坐标与图形,理解题意,正确得到原点可能位置是解答的关键.
7.B
【分析】根据题意,结合坐标系中a,b的最值,分析得出的最大值与最小值即可
【详解】解:根据题意,当取最大值时,即a最小,b最大,则,
∴的最大值是3,
当取最小值时,即a最大,b最小,则,
∴的最小值是.
故选:B.
【点睛】此题考查了坐标与图形的性质,解题关键是根据题意找出a,b的最值.
8.B
【分析】根据旋转的性质分别求出第1、2、3、4s时,点A的对应点、、、的坐标,找到规律,进而得出第时,点A的对应点的坐标.
【详解】解:∵,
∴A在第一象限的角平分线上,
∵叶片每秒绕原点顺时针转动,
∴,,,,
∴点A的坐标以每4秒为一个周期依次循环,
∵,
∴第时,点A的对应点的坐标与相同,为.
故选:B.
【点睛】本题考查了旋转的性质,点的坐标,找到点A的坐标循环的规律是解题的关键.
9.B
【分析】利用图形寻找规律,再利用规律解题即可.
【详解】解:第1圈有1个点,即,这时;
第2圈有8个点,即到;
第3圈有16个点,即到,;
依次类推,第n圈,;
由规律可知:是在第23圈上,且,则即,故A选项不正确;
是在第23圈上,且,即,故B选项正确;
第n圈,,所以,故C、D选项不正确;
故选B.
【点睛】本题考查图形与规律,利用所给的图形找到规律是解题的关键.
10.C
【分析】由题得,点A、B、P、Q、M、N都在双扭线上,计算的面积,观察图形,即可判断各个结论.
【详解】解:如图,连接,
得,,
∴双扭线围成的面积大于6,故①不正确;
由图得,双扭线内部包含4个整数点,
边界上有7个整数点,
共11个,故②正确;
由图得,点A、B与原点距离最大为3,故③正确;
设的高为h,
∵,且,
∴,
由图得,点P、Q、M、N均满足题意,故④正确,
故选:C.
【点睛】本题考查了在坐标系中判断点的位置,合理的推断及计算是解题关键.
11.东经,南纬
【分析】根据题意可得第一个数是经度,西为正,东为负,第二个数为纬度,南为正,北为负,据此,即可求解.
【详解】解:依题意,有序实数对,的含义是东经,南纬
故答案为:东经,南纬.
【点睛】本题考查了有序实数对表示位置,正负数的意义,理解题意是解题的关键.
12.第二象限
【解析】略
13.
【分析】先根据点A和点B的坐标建立平面直角坐标系,然后写出点C的坐标.
【详解】如图,
∴点C的坐标为.
故答案为:.
【点睛】本题考查了用坐标表示位置,正确建立平面直角坐标系是解答本题的关键.
14.祝你成功
【分析】先确定原文坐标,再根据密码钥匙,转化为译文即可.
【详解】设每个正方形的边长是一个单位长度,
∵正的坐标为,做的坐标为,数的坐标为,学的坐标为,
∴译文坐标分别是,,, ,译文为祝你成功,
故答案为:祝你成功.
【点睛】本题考查了坐标表示位置,熟练掌握坐标与位置的关系是解题的关键.
15.
【分析】本题考查了坐标位置的确定,根据题目条件找出横坐标和纵坐标的规律是解题的关键,规律性强,难度较大,根据规律性找出横坐标和纵坐标的规律公式,然后把代入进行计算即可求解.
【详解】解:当n为偶数时,;
当n为奇数时,.
∴依次为1,2,1,2,…;依次为1,1,2,2,3,3,….
∴,
∴第个点的坐标为.
16.见解析
【分析】本题考查作图-应用与涉及作图,根据题意画出图形即可.
【详解】解:如图:
17.(1)苏,冀
(2),
(3)见解析
【分析】(1)根据点A和点B的坐标,即可找到的位置;
(2)参照的位置,可得其他交叉道口的坐标;
(3)答案不唯一,要求路程总长最短即可.
【详解】(1)解:此时是苏街与冀路的交叉道口,
故答案为:苏,冀;
(2)以苏街与冀路的交叉道口为,
则渝街与陕路交叉道口的坐标记作,
沪街与京路交叉道口的坐标记作,
故答案为:,;
(3)最短路线可以为:—————,
或—————.
【点睛】本题考查了确定位置,解题的关键是用已知点的位置做参照,找到其他位置.
18.(1)
(2)见解析,的面积6
(3)见详解
【分析】(1)因为轴,点C与点纵坐标相等,点C在y轴右侧,且,即可求出横坐标;
(2)利用三角形面积求解即可;
(3)利用“垂线段最短”,解答即可.
【详解】(1)解:轴,,点C在y轴右侧,且.
∴点C的坐标为:;
故答案为:;
(2)如图:
的面积:
(3)
当线段AP长度最小时,点P的坐标为,依据是直线外一点与直线上各点连线中垂线段最短.
【点睛】本题考查了作图-复杂作图,坐标与图形性质,解答本题的关键是准确作图.
19.(1)或
(2)见解析,;()
【分析】(1)平移,使点与点重合,然后确定和点坐标即可;
(2)利用矩形的对角线互相平分得到点,作图写出坐标即可.
【详解】(1)解:如图,
(2)如图,
点M为所作,M点的坐标为()
故答案为:;().
【点睛】本题考查了作图,基本作图,坐标与图形性质,熟练结合以上知识准确作图并写出坐标是解题的关键.
20.(1)
(2)
(3)①详见解析;②平行且相等;(,)③
【分析】(1)根据轴上的点的横坐标为0,进而得出,代入点坐标,即可求解;
(2)根据点在轴上,轴,且点,求得点的坐标;
(3)①根据的坐标,将横坐标都减去2,得到,顺次连接得到三角形;
②根据平移的性质可得,;
③根据坐标以及平行四边形的面积公式即可求解.
【详解】(1)解:∵点,且点在轴上;
∴,解得:,
∴
∴;
故答案为:;
(2)解:∵轴,且点,
∴的横坐标为,
又点在轴上,
∴,
∴故答案为:;
(3)①如图,三角形即为所求;
②根据平移的性质可得,
故答案为:平行且相等;(,).
③四边形面积为4.
【点睛】本题考查了坐标与图形,平移作图,平移的性质,熟练掌握以上知识是解题的关键.
21.(1)
(2)或;
(3)满足条件的点的坐标为或.
【分析】(1)利用矩形的性质求出,,可得结论;
(2)分两种情形:如图1中,当点在线段上时,如图2中,当点在线段上时,分别构建方程求解;
(3)当点与重合时,的面积为3,此时,过点作交于点,此时,的面积为3,求出坐标即可.
【详解】(1)解:四边形是矩形,,,
,,
,
故答案为:;
(2)解:如图1中,当点在线段上时,
由题意,,
,
.
如图2中,当点在线段上时,
由题意,,
,
.
综上所述,满足条件的的值为或;
(3)解:如图3中,
当点与重合时,的面积为3,此时,
过点作交于点,此时,的面积为3,
,
综上所述,满足条件的点的坐标为或.
【点睛】本题属于四边形综合题,考查了矩形的性质,三角形的面积等知识,解题的关键是学会用分类讨论的思想思考问题,学会利用参数构建方程解决问题.
22.(1)①,②相等,③平行;(2)点的坐标是或;(3)
【分析】(1)①根据点的坐标是,点的坐标是,,可知,,进而即可解答;②点的坐标是,点的坐标是,,可知,,,进而即可解答;③根据点的坐标是,点的坐标是,横坐标相等即可解答;
(2)根据设点,根据面积相等,再根据可知进而即可解答;
(3)根据可知进而即可解答.
【详解】解:(1)①∵点的坐标是,点的坐标是,,,
∴ ,,,
∴,,
故答案为;
②∵点的坐标是,点的坐标是,,
∴,,,,
∴,
∴,
∴,
故答案为;
③∵点的坐标是,点的坐标是,,
∴三点的横坐标相等,
∴三点所在的直线与x轴的位置关系是平行.
(2)∵设点,在平面直角坐标系内取一点,连接,
过点作轴的垂线交轴于,过点作轴的垂线交轴于点,
∵,
∴,
∴,
∵,
∴,
∴,
∴,
∵点在轴上方,
∴,
∵,,,,
∴,
∴,
∴,
∴或,
(3)设,
∵点的坐标是,点的坐标是,, ,点的坐标是,
∴,,,,,,
∵,
∴,
∴,
∴,
∴,
∴,
∴,
∵不符合题意,
∴,
∴点.
【点睛】本题考查了平面直角坐标系内点的坐标特征,平行于轴的点的坐标特征,三角形的面积与平面直角坐标系,掌握平面直角坐标系内点的坐标特征是解题的关键.
23.(1),
(2)存在,或
(3)①,②不变,3
【分析】(1)非负性求出的值,进而得到点坐标,再根据平移的性质,求出点的坐标即可;
(2)设点,根据三角形的面积等于三角形的面积,列出方程求解即可;
(3)①过点作,平移得到,进而得到,根据平行线的性质,推出,即可;
②设交于点,由①可知:,根据给定的角度之间的关系,结合三角形的内角和定理,求出,进一步得出结果即可.
【详解】(1)解:∵,
∴,
∴,
∴,
∵平移后的点的坐标为,
∴,即:;
故答案为:,;
(2)∵,
∴,
设点,
∴,
∴;
∴或;
(3)①过点作,
∵,
∴,
∴,
∴,,
∴;
②不变,设交于点,则:,
∵,,
∴,,
由①知:,
∴,
∴,
∴,
∴,为定值.
【点睛】本题考查非负性,坐标与图形变换—平移,平行线的判定和性质,三角形的内角和定理,熟练掌握平移的性质,求出点的坐标,利用数形结合的思想进行求解,是解题的关键.
答案第1页,共2页
