13.2多边形 课件(共21张PPT)青岛版数学七年级下册
文档属性
| 名称 | 13.2多边形 课件(共21张PPT)青岛版数学七年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-21 23:26:12 | ||
图片预览







文档简介
(共21张PPT)
13.2 多边形
七年级下册第十三单元
学习目标
1.了解多边形的定义,多边形的边、内角、外角、顶点、对角线等概念。
2.认识正多边形,会根据边数说出正多边形的名称。
3.探索并掌握多边形的内角和与外角和公式,培养学生的空间观念和几何直观,发展学生的合情推理和演绎推理能力。
4.会用多边形的内角和与外角和公式进行简单的计算与说理。
探究新知
观察并思考:以下图形有什么共同特征?
探究新知
平面内,若干条线段首尾顺次相接,且有公共端点的线段不在同一条直线上,这样得到的图形叫做多边形。
组成多边形的各条线段叫做多边形的边,
它们的公共端点叫做多边形的顶点,
相邻两条边所组成的角叫做多边形的内角,简称多边形的角。
注意:①多边形有几条边就是几边形,三角形是最简单的多边形
②n边形的边数、顶点数、内角数都等于n
③两点确定一条直线;不在同一平面的三点确定一个平面
顶点
内角
边
对角线
对角线:连接多边形不相邻的两个顶点的线段.
A
B
C
D
E
表示:五边形ABCDE或五边形DCBAE
探究新知
边数 3 4 5 6 7 … n
从一个顶点出发的对角线的条数
上述对角线分成的三角形个数 …
总的对角线条数 …
0
1
0
1
2
2
2
3
5
3
4
9
4
5
14
n-3
n-2
探究新知
n边形的对角线条数为
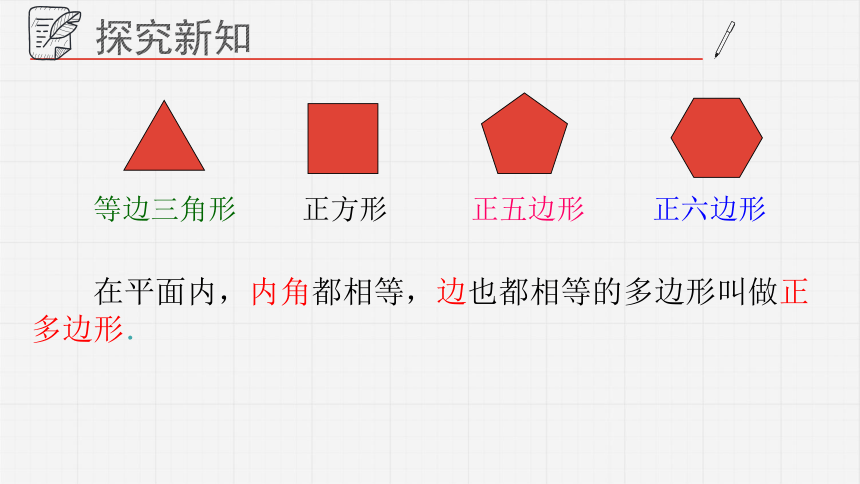
在平面内,内角都相等,边也都相等的多边形叫做正多边形.
等边三角形
正方形
正五边形
正六边形
探究新知
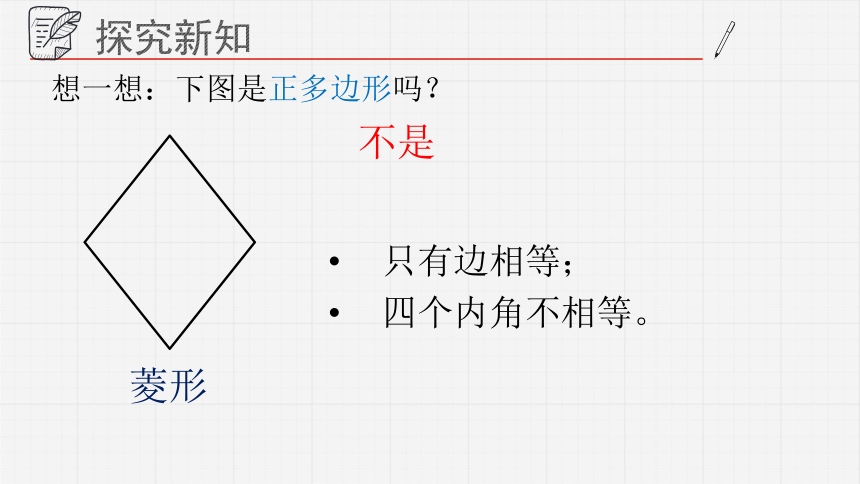
想一想:下图是正多边形吗?
菱形
不是
只有边相等;
四个内角不相等。
探究新知
即学即练
1.下列图形中不可能是正多边形的是( )
A.三角形 B.正方形 C.四边形 D.梯形
D
2.已知一个多边形有35条对角线,你能求出它的边数吗?
解:
=35
即 n2-3n-70=0
(n-10)(n+7)=0
解之,得n=10或n=-7(舍)
探究新知
(1)一个三角形的内角和是多少度?
(2)一个正方形的内角和是多少度?一个长方形呢?
(3)五边形的内角和是多少度?如何计算?
A
C
D
E
B
五边形内角和 =3×180°=540°
多边形 边数 分成三角形的个数 图形 内角和 计算规律
三角形
四边形
五边形
六边形
... ... ... ... ... ...
n边形
180°
360°
540°
720°
探究新知
3
4
5
6
n
1
n-2
2
3
4
(n-2) ·180°
4 ×180°
3 ×180°
2 ×180°
1 ×180°
(n-2) ·180°
总结:n边形内角和公式
B
A
C
D
G
F
E
n边形内角和=(n-2) ·180°
探究新知
正多边形每个内角为 =
1800
180
六
十
即学即练
1、十二边形的内角和是( )。
2、一个多边形当边数增加1时,它的内角和增加( )。
3、一个多边形的内角和是720 ,则此多边形共有( )个内角。
4、如果一个多边形的内角和是1440度,那么这是( )边形。
探究新知
A
B
C
D
E
多边形一个角的一边与另一边的反向延长线所组成的角,叫做多边形的外角.
思考:1.任意一个外角与它相邻的内角有什么关系?
2.五个外角加上它们分别相邻的五个内角和是多少?
3.这五个平角和与五边形的内角和、外角和有什么关系?
探究新知
A
B
C
D
E
互补
5×180°=900°
五边形的外角和=5个平角-五边形的内角和
= 360 °
= 5×180°-(5-2) × 180°
结论:五边形的外角和等于360°
探究新知
A
E
B
C
D
F
n
结论:n边形的外角和等于360°
=360 °
n边形外角和= n个平角 - n边形内角和
=n×180 °- (n-2) × 180°
在n边形的每个顶点处各取一个外角,这些外角的和叫做n边形的外角和.
即学即练
思考:正多边形每个外角的度数怎样计算?
∵正多边形外角和为360°
∴正多边形每个外角为
练习1:如果一个多边形的每一个外角等于30°,则这个多边形的边数是_____.
n×30°= 360°
n = 12
解:n边形外角和 = 360 °
练习2:正五边形的每一个外角等于____,每一个内角等于_____。
5x = 360°
x = 72°
72°
108°
所以每一个内角度数为180-72°= 108 °
即学即练
解:设正五边形的每一个外角度数为x,由多边形的外角和等于360°可得:
1.n边形的内角和等于__________,九边形的内角和等于___________.
2.如果一个多边形的内角和是1440度,那么这是____边形。
3.已知多边形的每个内角都等于150°,求这个多边形的边数?
4.一个多边形从一个顶点可引对角线3条,这个多边形内角和等于( )
A.360° B.540° C.720° D.900°
5.已知一个多边形,它的内角和等于外角和的2倍,求这个多边形的边数?
即学即练
课堂小结
对角线:连接多边形不相邻的两个顶点的线段.
n边形的对角线条数为
n边形内角和=(n-2) ·180°
正多边形每个内角为 =
n边形的外角和等于360°
课后作业
作业:
P146、练习;13.2
同步练习册
13.2 多边形
七年级下册第十三单元
学习目标
1.了解多边形的定义,多边形的边、内角、外角、顶点、对角线等概念。
2.认识正多边形,会根据边数说出正多边形的名称。
3.探索并掌握多边形的内角和与外角和公式,培养学生的空间观念和几何直观,发展学生的合情推理和演绎推理能力。
4.会用多边形的内角和与外角和公式进行简单的计算与说理。
探究新知
观察并思考:以下图形有什么共同特征?
探究新知
平面内,若干条线段首尾顺次相接,且有公共端点的线段不在同一条直线上,这样得到的图形叫做多边形。
组成多边形的各条线段叫做多边形的边,
它们的公共端点叫做多边形的顶点,
相邻两条边所组成的角叫做多边形的内角,简称多边形的角。
注意:①多边形有几条边就是几边形,三角形是最简单的多边形
②n边形的边数、顶点数、内角数都等于n
③两点确定一条直线;不在同一平面的三点确定一个平面
顶点
内角
边
对角线
对角线:连接多边形不相邻的两个顶点的线段.
A
B
C
D
E
表示:五边形ABCDE或五边形DCBAE
探究新知
边数 3 4 5 6 7 … n
从一个顶点出发的对角线的条数
上述对角线分成的三角形个数 …
总的对角线条数 …
0
1
0
1
2
2
2
3
5
3
4
9
4
5
14
n-3
n-2
探究新知
n边形的对角线条数为
在平面内,内角都相等,边也都相等的多边形叫做正多边形.
等边三角形
正方形
正五边形
正六边形
探究新知
想一想:下图是正多边形吗?
菱形
不是
只有边相等;
四个内角不相等。
探究新知
即学即练
1.下列图形中不可能是正多边形的是( )
A.三角形 B.正方形 C.四边形 D.梯形
D
2.已知一个多边形有35条对角线,你能求出它的边数吗?
解:
=35
即 n2-3n-70=0
(n-10)(n+7)=0
解之,得n=10或n=-7(舍)
探究新知
(1)一个三角形的内角和是多少度?
(2)一个正方形的内角和是多少度?一个长方形呢?
(3)五边形的内角和是多少度?如何计算?
A
C
D
E
B
五边形内角和 =3×180°=540°
多边形 边数 分成三角形的个数 图形 内角和 计算规律
三角形
四边形
五边形
六边形
... ... ... ... ... ...
n边形
180°
360°
540°
720°
探究新知
3
4
5
6
n
1
n-2
2
3
4
(n-2) ·180°
4 ×180°
3 ×180°
2 ×180°
1 ×180°
(n-2) ·180°
总结:n边形内角和公式
B
A
C
D
G
F
E
n边形内角和=(n-2) ·180°
探究新知
正多边形每个内角为 =
1800
180
六
十
即学即练
1、十二边形的内角和是( )。
2、一个多边形当边数增加1时,它的内角和增加( )。
3、一个多边形的内角和是720 ,则此多边形共有( )个内角。
4、如果一个多边形的内角和是1440度,那么这是( )边形。
探究新知
A
B
C
D
E
多边形一个角的一边与另一边的反向延长线所组成的角,叫做多边形的外角.
思考:1.任意一个外角与它相邻的内角有什么关系?
2.五个外角加上它们分别相邻的五个内角和是多少?
3.这五个平角和与五边形的内角和、外角和有什么关系?
探究新知
A
B
C
D
E
互补
5×180°=900°
五边形的外角和=5个平角-五边形的内角和
= 360 °
= 5×180°-(5-2) × 180°
结论:五边形的外角和等于360°
探究新知
A
E
B
C
D
F
n
结论:n边形的外角和等于360°
=360 °
n边形外角和= n个平角 - n边形内角和
=n×180 °- (n-2) × 180°
在n边形的每个顶点处各取一个外角,这些外角的和叫做n边形的外角和.
即学即练
思考:正多边形每个外角的度数怎样计算?
∵正多边形外角和为360°
∴正多边形每个外角为
练习1:如果一个多边形的每一个外角等于30°,则这个多边形的边数是_____.
n×30°= 360°
n = 12
解:n边形外角和 = 360 °
练习2:正五边形的每一个外角等于____,每一个内角等于_____。
5x = 360°
x = 72°
72°
108°
所以每一个内角度数为180-72°= 108 °
即学即练
解:设正五边形的每一个外角度数为x,由多边形的外角和等于360°可得:
1.n边形的内角和等于__________,九边形的内角和等于___________.
2.如果一个多边形的内角和是1440度,那么这是____边形。
3.已知多边形的每个内角都等于150°,求这个多边形的边数?
4.一个多边形从一个顶点可引对角线3条,这个多边形内角和等于( )
A.360° B.540° C.720° D.900°
5.已知一个多边形,它的内角和等于外角和的2倍,求这个多边形的边数?
即学即练
课堂小结
对角线:连接多边形不相邻的两个顶点的线段.
n边形的对角线条数为
n边形内角和=(n-2) ·180°
正多边形每个内角为 =
n边形的外角和等于360°
课后作业
作业:
P146、练习;13.2
同步练习册
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
