六年级上册数学人教版分数除法例7课件(共23张PPT)
文档属性
| 名称 | 六年级上册数学人教版分数除法例7课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-22 06:04:42 | ||
图片预览





文档简介
(共23张PPT)
分数除法 例7
人教版数学六年级上册第三单元
复习旧知
甲队单独修一条路,每天修50米,修完用了20天,这条路有多长?
乙队单独修一条长1000米的路,每天修50米,修完要多少天?
甲队单独修一条长1000米的路,修完要25天,甲队每天修多少米?
甲乙两队合作同时修一条长1000米的路,甲队每天修50米,乙队每天修30米,修完这条路需要多少天?
50×20=1000(米)
1000÷50=20(天)
1000÷25=40(米)
1000÷(50+30)= 12.5(天)
工程问题
如果两队合修,多少天能修完?
假设法
引入情境,探究新知
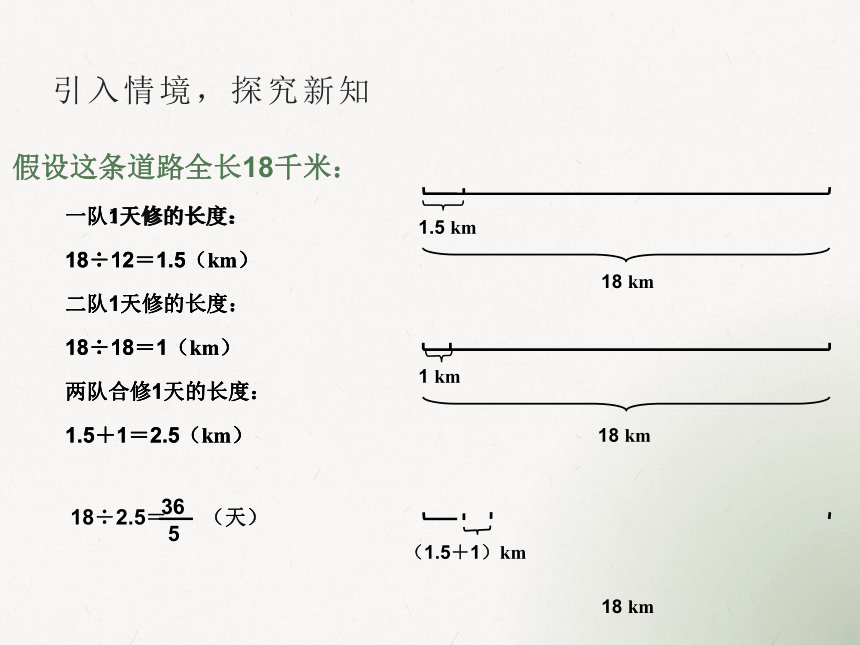
假设这条道路全长18千米:
1.5 km
18 km
一队1天修的长度:
18÷12=1.5(km)
二队1天修的长度:
18÷18=1(km)
两队合修1天的长度:
1.5+1=2.5(km)
一队1天修的长度:
18÷12=1.5(km)
二队1天修的长度:
18÷18=1(km)
两队合修1天的长度:
1.5+1=2.5(km)
18÷2.5= (天)
5
36
18 km
1 km
(1.5+1)km
18 km
引入情境,探究新知
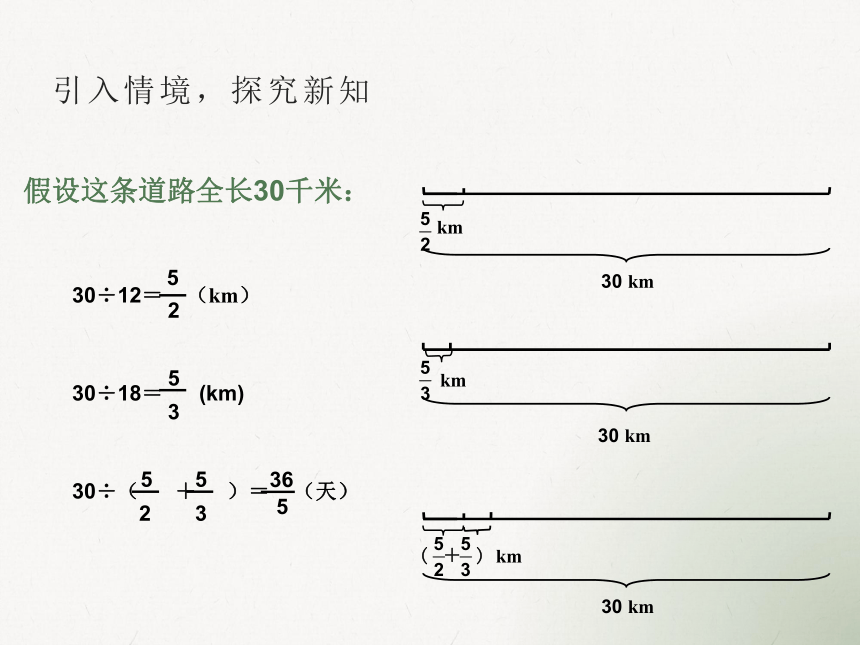
30÷12= (km)
30÷18= (km)
30÷( + )= (天)
2
5
3
5
2
5
3
5
5
36
假设这条道路全长30千米:
km
30 km
km
30 km
30 km
( ) km
引入情境,探究新知
对比发现
问题:
① 我们假设这条路的长度都不同,但最终的结果是相同的。
②想一想:如果把这条路的长度看做是“1”,行不行?
应该怎样解答?
36÷12=1.5(km)
18÷18=1(km)
18÷(1.5+1)= (天)
5
36
30÷12= (km)
30÷18= (km)
30÷( + )= (天)
2
5
3
5
5
36
3
5
2
5
引入情境,探究新知
“1”
“1”
“1”
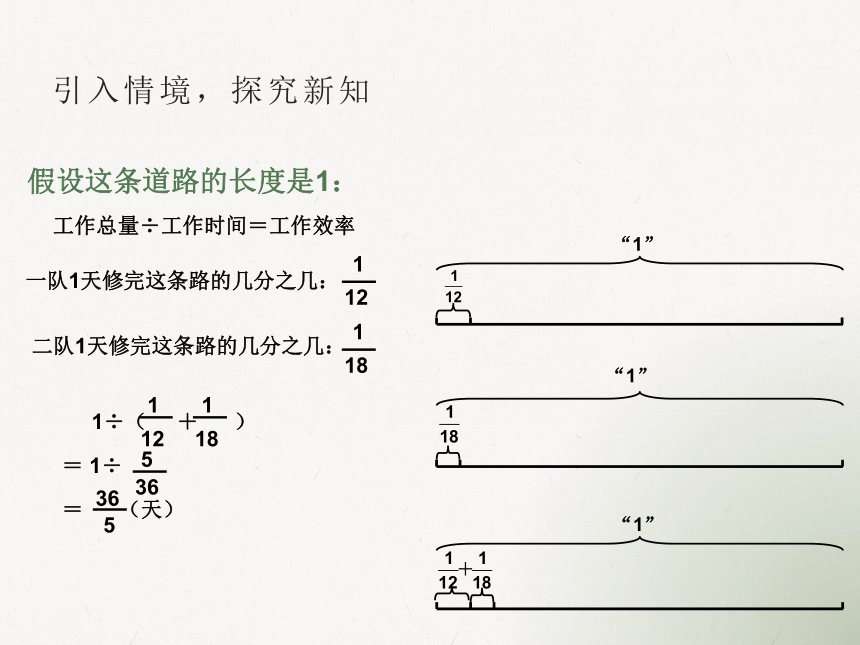
1÷( + )
= 1÷
= (天)
18
1
12
1
36
5
5
36
假设这条道路的长度是1:
工作总量÷工作时间=工作效率
一队1天修完这条路的几分之几:
18
1
二队1天修完这条路的几分之几:
12
1
引入情境,探究新知
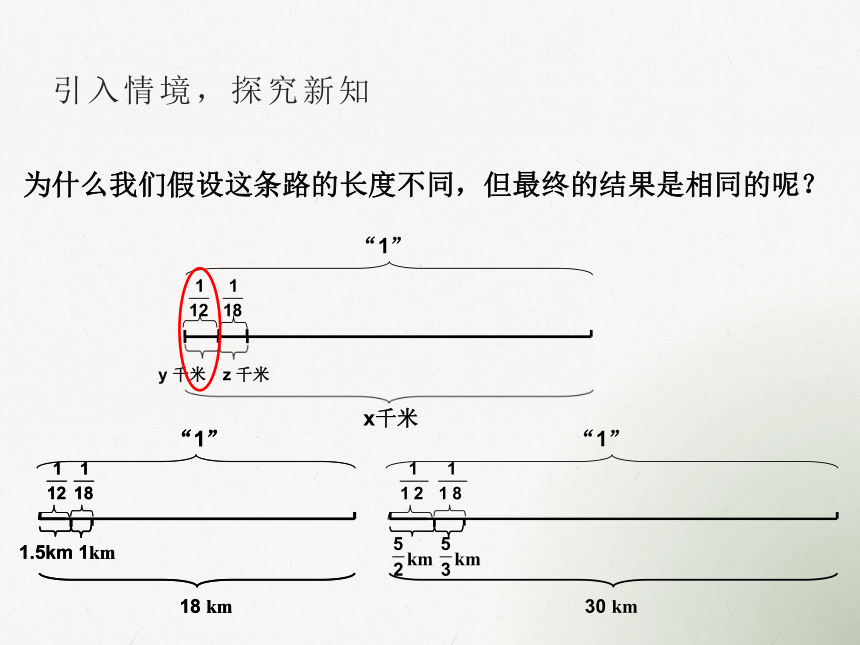
为什么我们假设这条路的长度不同,但最终的结果是相同的呢?
“1”
y 千米
x千米
z 千米
1.5km 1km
18 km
“1”
km
30 km
“1”
km
1.5km 1km
18 km
“1”
我发现了:
方法1:
方法2:
18÷12=1.5(km)
18÷18=1(km)
18÷(1.5+1)= (天)
5
36
30÷12= (km)
30÷18= (km)
30÷( + )= (天)
2
5
3
5
2
5
3
5
5
36
1÷( + )
= 1÷
= (天)
18
1
12
1
36
5
5
36
方法3:
巩固练习,提升认识
如果两辆车一起运,多少次能运完这批货物?
1÷( + )
=1÷
=2(次)
6
1
3
1
2
1
答:如果两辆车一起运,2次能运完这批货物。
解决问题
方法1:
300÷8=37.5(棵)
300÷10=30(棵)
300÷(37.5+30)= (天)
天<5天
方法2:
1÷8=
1÷10=
1÷( + )= (天)
天<5天
答:5天能种完。
巩固练习,提升认识
1÷( + )
=1÷
=12(天)
20
1
30
1
12
1
挖一条水渠,王伯伯每天挖整条水渠的 ,李叔叔每天挖整条
水渠的 。两人合作,几天能挖完?
20
1
30
1
答:两人合作,12天能挖完。
课后巩固
甲车从A城市到B城市要行驶2小时,乙车从B城市到A城市要行驶3小时。两车同时分别从A城市和B城市出发,几小时后相遇?
1÷( + )
=1÷
=1. 2(天)
2
1
3
1
6
5
答:两车同时分别从A城市和B城市出发,1.2小时后相遇。
“1”
“1”
“1”
三、解决问题
小明和爷爷一起去操场散步。小明走一圈需要8分钟,爷爷走一圈需要10分钟。
(1)如果两人同时同地出发,相背而行,多少分钟后相遇?
爷爷和小明相背而行同时出发,相遇时他们正好走了一圈。
爷爷和小明的速度怎样表示呢?
三、解决问题
小明和爷爷一起去操场散步。小明走一圈需要8分钟,爷爷走一圈需要10分钟。
(1)如果两人同时同地出发,相背而行,多少分钟后相遇?
相遇
操场全长
起点
相遇
三、解决问题
小明和爷爷一起去操场散步。小明走一圈需要8分钟,爷爷走一圈需要10分钟。
(1)如果两人同时同地出发,相背而行,多少分钟后相遇?
1÷8=
1÷10=
1÷( + )
=1 ÷
= (分)
三、解决问题
小明和爷爷一起去操场散步。小明走一圈需要8分钟,爷爷走一圈需要10分钟。
阅读与理解
(2)如果两人同时同地出发,同方向而行,多少分钟后小明超出爷爷一整圈?
同向而行,为什么小明能超出爷爷一圈呢?
同方向而行是怎样运动呢?
三、解决问题
小明和爷爷一起去操场散步。小明走一圈需要8分钟,爷爷走一圈需要10分钟。
操场全长
起点
(2)如果两人同时同地出发,同方向而行,多少分钟后小明超出爷爷一整圈?
一共比爷爷多走一个操场全长
每分钟小明比爷爷多走的长度
三、解决问题
小明和爷爷一起去操场散步。小明走一圈需要8分钟,爷爷走一圈需要10分钟。
(2)如果两人同时同地出发,同方向而行,多少分钟后小明超出爷爷一整圈?
分析与解答
1÷10=
1÷8=
1÷( - )
=1÷
=20(分)
回顾与反思
小明每分钟能超出爷爷多少呢?你有办法知道吗?
这道题还有其他的
解决办法吗?
(二)分析与解答
问题:
① 这样列式的依据是什么?
“1”
“1”
“1”
1÷( + )
= 1÷
= (天)
18
1
12
1
36
5
5
36
求的是什么? 呢?
12
1
18
1
③“ + ”求的是什么?
12
1
18
1
(二)分析与解答
问题:
② 为什么我们假设这条路的长度不同,但最终的结果是相同的呢?
“1”
1.5 km
18 km
1 km
① “1.5 km和 ”都在表示一队1天修的长度,有什么不一样呢?
(都是在表示一队1天的工作量,一个是具体数量,一个是1天的工
作量占这条路的几分之几。)
12
1
(三)回顾与反思
问题:
我们把道路假设成不同的长度,得出了相同的结果,这个结果对吗?可以怎样检验?
小结:
不管假设这条道路的长度是多少,答案都是相同的,把这条路的长度假设成是单位“1”,在计算时是比较简便的。
预设1:
看看这条路的 是不是1.5 km
18× =1.5(km)
12
1
12
1
预设2:
看看一队1天修的是不是全长的
1.5÷18 =
12
1
12
1
分数除法 例7
人教版数学六年级上册第三单元
复习旧知
甲队单独修一条路,每天修50米,修完用了20天,这条路有多长?
乙队单独修一条长1000米的路,每天修50米,修完要多少天?
甲队单独修一条长1000米的路,修完要25天,甲队每天修多少米?
甲乙两队合作同时修一条长1000米的路,甲队每天修50米,乙队每天修30米,修完这条路需要多少天?
50×20=1000(米)
1000÷50=20(天)
1000÷25=40(米)
1000÷(50+30)= 12.5(天)
工程问题
如果两队合修,多少天能修完?
假设法
引入情境,探究新知
假设这条道路全长18千米:
1.5 km
18 km
一队1天修的长度:
18÷12=1.5(km)
二队1天修的长度:
18÷18=1(km)
两队合修1天的长度:
1.5+1=2.5(km)
一队1天修的长度:
18÷12=1.5(km)
二队1天修的长度:
18÷18=1(km)
两队合修1天的长度:
1.5+1=2.5(km)
18÷2.5= (天)
5
36
18 km
1 km
(1.5+1)km
18 km
引入情境,探究新知
30÷12= (km)
30÷18= (km)
30÷( + )= (天)
2
5
3
5
2
5
3
5
5
36
假设这条道路全长30千米:
km
30 km
km
30 km
30 km
( ) km
引入情境,探究新知
对比发现
问题:
① 我们假设这条路的长度都不同,但最终的结果是相同的。
②想一想:如果把这条路的长度看做是“1”,行不行?
应该怎样解答?
36÷12=1.5(km)
18÷18=1(km)
18÷(1.5+1)= (天)
5
36
30÷12= (km)
30÷18= (km)
30÷( + )= (天)
2
5
3
5
5
36
3
5
2
5
引入情境,探究新知
“1”
“1”
“1”
1÷( + )
= 1÷
= (天)
18
1
12
1
36
5
5
36
假设这条道路的长度是1:
工作总量÷工作时间=工作效率
一队1天修完这条路的几分之几:
18
1
二队1天修完这条路的几分之几:
12
1
引入情境,探究新知
为什么我们假设这条路的长度不同,但最终的结果是相同的呢?
“1”
y 千米
x千米
z 千米
1.5km 1km
18 km
“1”
km
30 km
“1”
km
1.5km 1km
18 km
“1”
我发现了:
方法1:
方法2:
18÷12=1.5(km)
18÷18=1(km)
18÷(1.5+1)= (天)
5
36
30÷12= (km)
30÷18= (km)
30÷( + )= (天)
2
5
3
5
2
5
3
5
5
36
1÷( + )
= 1÷
= (天)
18
1
12
1
36
5
5
36
方法3:
巩固练习,提升认识
如果两辆车一起运,多少次能运完这批货物?
1÷( + )
=1÷
=2(次)
6
1
3
1
2
1
答:如果两辆车一起运,2次能运完这批货物。
解决问题
方法1:
300÷8=37.5(棵)
300÷10=30(棵)
300÷(37.5+30)= (天)
天<5天
方法2:
1÷8=
1÷10=
1÷( + )= (天)
天<5天
答:5天能种完。
巩固练习,提升认识
1÷( + )
=1÷
=12(天)
20
1
30
1
12
1
挖一条水渠,王伯伯每天挖整条水渠的 ,李叔叔每天挖整条
水渠的 。两人合作,几天能挖完?
20
1
30
1
答:两人合作,12天能挖完。
课后巩固
甲车从A城市到B城市要行驶2小时,乙车从B城市到A城市要行驶3小时。两车同时分别从A城市和B城市出发,几小时后相遇?
1÷( + )
=1÷
=1. 2(天)
2
1
3
1
6
5
答:两车同时分别从A城市和B城市出发,1.2小时后相遇。
“1”
“1”
“1”
三、解决问题
小明和爷爷一起去操场散步。小明走一圈需要8分钟,爷爷走一圈需要10分钟。
(1)如果两人同时同地出发,相背而行,多少分钟后相遇?
爷爷和小明相背而行同时出发,相遇时他们正好走了一圈。
爷爷和小明的速度怎样表示呢?
三、解决问题
小明和爷爷一起去操场散步。小明走一圈需要8分钟,爷爷走一圈需要10分钟。
(1)如果两人同时同地出发,相背而行,多少分钟后相遇?
相遇
操场全长
起点
相遇
三、解决问题
小明和爷爷一起去操场散步。小明走一圈需要8分钟,爷爷走一圈需要10分钟。
(1)如果两人同时同地出发,相背而行,多少分钟后相遇?
1÷8=
1÷10=
1÷( + )
=1 ÷
= (分)
三、解决问题
小明和爷爷一起去操场散步。小明走一圈需要8分钟,爷爷走一圈需要10分钟。
阅读与理解
(2)如果两人同时同地出发,同方向而行,多少分钟后小明超出爷爷一整圈?
同向而行,为什么小明能超出爷爷一圈呢?
同方向而行是怎样运动呢?
三、解决问题
小明和爷爷一起去操场散步。小明走一圈需要8分钟,爷爷走一圈需要10分钟。
操场全长
起点
(2)如果两人同时同地出发,同方向而行,多少分钟后小明超出爷爷一整圈?
一共比爷爷多走一个操场全长
每分钟小明比爷爷多走的长度
三、解决问题
小明和爷爷一起去操场散步。小明走一圈需要8分钟,爷爷走一圈需要10分钟。
(2)如果两人同时同地出发,同方向而行,多少分钟后小明超出爷爷一整圈?
分析与解答
1÷10=
1÷8=
1÷( - )
=1÷
=20(分)
回顾与反思
小明每分钟能超出爷爷多少呢?你有办法知道吗?
这道题还有其他的
解决办法吗?
(二)分析与解答
问题:
① 这样列式的依据是什么?
“1”
“1”
“1”
1÷( + )
= 1÷
= (天)
18
1
12
1
36
5
5
36
求的是什么? 呢?
12
1
18
1
③“ + ”求的是什么?
12
1
18
1
(二)分析与解答
问题:
② 为什么我们假设这条路的长度不同,但最终的结果是相同的呢?
“1”
1.5 km
18 km
1 km
① “1.5 km和 ”都在表示一队1天修的长度,有什么不一样呢?
(都是在表示一队1天的工作量,一个是具体数量,一个是1天的工
作量占这条路的几分之几。)
12
1
(三)回顾与反思
问题:
我们把道路假设成不同的长度,得出了相同的结果,这个结果对吗?可以怎样检验?
小结:
不管假设这条道路的长度是多少,答案都是相同的,把这条路的长度假设成是单位“1”,在计算时是比较简便的。
预设1:
看看这条路的 是不是1.5 km
18× =1.5(km)
12
1
12
1
预设2:
看看一队1天修的是不是全长的
1.5÷18 =
12
1
12
1
