第3单元比例易错精选题-数学六年级下册青岛版(含解析)
文档属性
| 名称 | 第3单元比例易错精选题-数学六年级下册青岛版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 424.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-24 17:01:48 | ||
图片预览

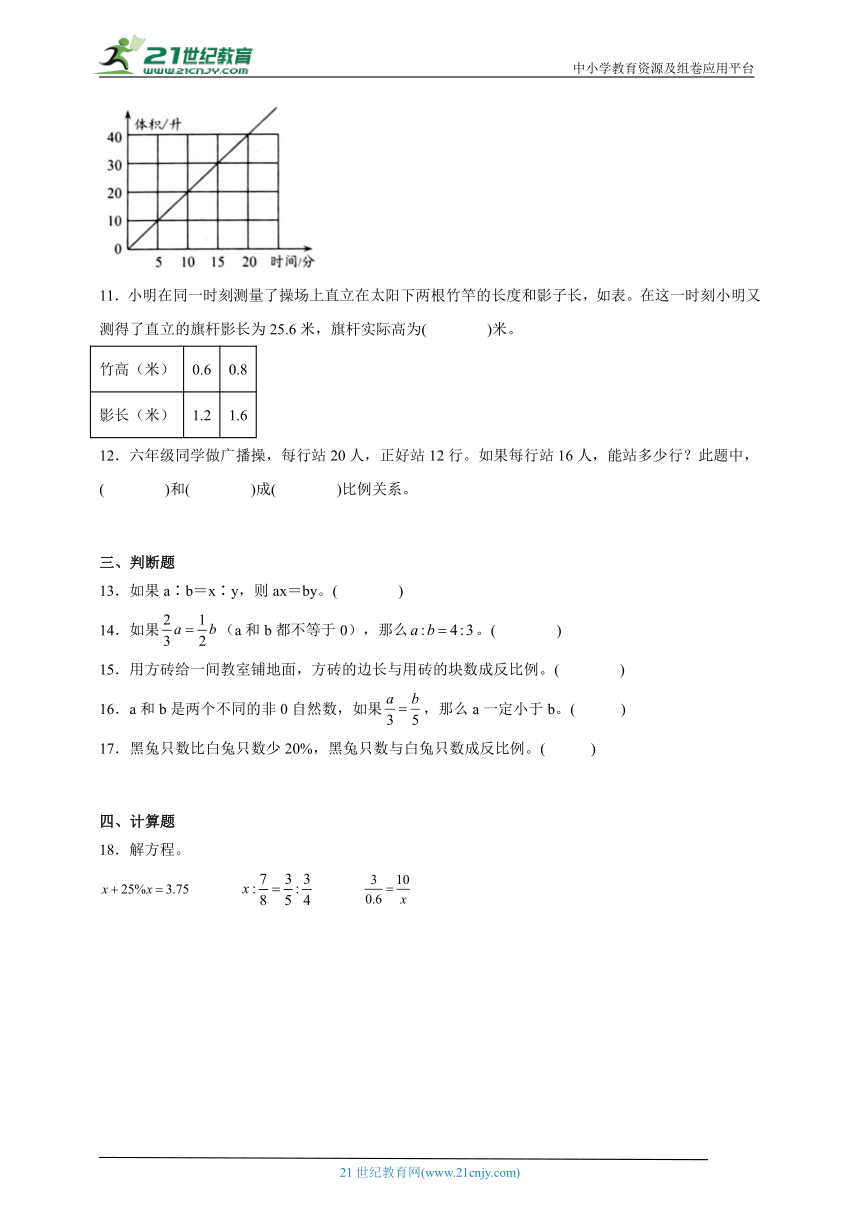



文档简介
中小学教育资源及组卷应用平台
第3单元比例易错精选题-数学六年级下册青岛版
一、选择题
1.解比例的依据是( )。
A.等式的基本性质 B.比的基本性质
C.比例的基本性质 D.比例的定义
2.下列选项中的两个量,成正比例关系的是( )。
A.圆柱的体积和底面积 B.一个人的身高和年龄
C.圆的周长和半径 D.飞机从北京飞往上海的速度和时间
3.下面各数量关系中,成反比例关系的是( )。
A.全班人数一定,缺勤人数和出勤人数 B.三角形的高一定,它的面积和底
C.正方形的边长和面积 D.一桶油,平均每天用去的千克数和用的天数
4.如果( ),那么x和成正比例(x、y均不为0)。
A. B. C. D.
5.我国逐渐完善养老金制度,居民可自行缴纳养老金。甲、乙两人计划用相同的年数分别缴纳养老金18万元和12万元。甲计划每年比乙多缴纳保险金0.2万元。若乙每年缴纳保险金x万元,则根据题意可列出比例为( )。
A. B.
C. D.
6.甲乙两个数均大于0,若甲的等于乙的,则甲、乙两数的比是( )。
A.9∶4 B.4∶1 C.3∶1 D.4∶3
二、填空题
7.解比例20∶25=4∶x的第一步是:20x=25×4,这一步利用了( )。
8.如果(m、n都不为0),那么( ),m和n成( )比例。
9.松树棵数的等于杨树棵数的,则松树与杨树的棵数比是( )。
10.如图,一根水管不停地向水箱注水,箱内水的体积不断变化。若箱内水的体积是45升,则注水( )分钟。
11.小明在同一时刻测量了操场上直立在太阳下两根竹竿的长度和影子长,如表。在这一时刻小明又测得了直立的旗杆影长为25.6米,旗杆实际高为( )米。
竹高(米) 0.6 0.8
影长(米) 1.2 1.6
12.六年级同学做广播操,每行站20人,正好站12行。如果每行站16人,能站多少行?此题中,( )和( )成( )比例关系。
三、判断题
13.如果a∶b=x∶y,则ax=by。( )
14.如果(a和b都不等于0),那么。( )
15.用方砖给一间教室铺地面,方砖的边长与用砖的块数成反比例。( )
16.a和b是两个不同的非0自然数,如果,那么a一定小于b。( )
17.黑兔只数比白兔只数少20%,黑兔只数与白兔只数成反比例。( )
四、计算题
18.解方程。
五、解答题
19.淘气模仿“曹冲称象”来称体重。淘气站在船上,船下沉2厘米;爸爸站在船上,船下沉4厘米。淘气的体重是35.7千克,爸爸的体重是多少千克?
20.一本故事书共150页,李丽3天看了45页,照这样的速度,看完这本书还需用多少天?(用比例解)
21.一辆中巴客车从甲地开往乙地,2小时行了120千米。照这样的速度,从聊城到烟台共540千米,需要几小时才能到达?(用比例解)
22.学校创客室的地面是正方形的,用边长是0.6米的方砖铺地,正好需要400块。如果改用边长是0.8米的方砖铺地,需要多少块?(用比例方法解荅)
23.科技的发展改善了我们的生活,也改变了人们的出行方式,人们可以选择的交通工具多种多样,如:地铁、汽车、高铁、火车、飞机等。据了解,从济南到郑州的公路长是440km。若一辆车2小时行了160km,照这样计算,从济南到郑州需要多少个小时?先说说路程和时间成什么比例,再用比例解。
24.抗击新冠肺炎期间,爷爷需要配制75%的酒精消毒,然而家里只有95%的酒精2400ml。小明利用本学期刚学过的相关知识,决心帮爷爷把家里95%的酒精稀释成75%,需要加水多少毫升的问题。
小明操作如下:
(1)把75%的酒精转化为:酒精与酒精溶液的比是3∶4。
(2)把95%的酒精转化为:酒精与酒精溶液的比19∶20。
接下来,请你帮小明算一算,需要加水多少毫升?
参考答案:
1.C
【分析】如果已经知道比例中的任意三项,根据比例的基本性质,可以求出比例中另一个未知项。求比例中的未知项,叫做解比例。
【详解】解比例的依据是比例的基本性质,即比例的两内项积=两外项积。
故答案为:C
2.C
【分析】根据x÷y=k(一定),x和y成正比例关系;xy=k(一定),x和y成反比例关系,进行分析。
【详解】A.圆柱的体积÷底面积=高,不确定高是否一定,无法确定圆柱的体积和底面积是否成正比例关系;
B.一个人的身高和年龄不成比例关系;
C.圆的周长÷半径=圆周率×2,圆的周长和半径成正比例关系;
D.北京到上海的距离一定,速度×时间=路程,飞机从北京飞往上海的速度和时间成反比例关系。
成正比例关系的是圆的周长和半径。
故答案为:C
3.D
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例;如果是其它的量一定或乘积、比值不一定,就不成比例。据此解答即可。
【详解】A.出勤人数+缺勤人数=总人数,总人数一定,出勤人数和缺勤人数不成比例关系;
B.因为三角形的面积=底×高×,所以三角形的面积÷底=高×(一定),符合x÷y=k(一定),所以三角形的高一定,它的面积和底成正比例;
C.正方形的面积=边长×边长,在这个关系中,边长发生变化,正方形的面积也发生变化,而正方形的另一个边长也随着发生了变化,三个量都是变化的,没有一定的量,所以正方形的边长和面积不成比例;
D.每天用的千克数×所用的天数=这桶油的质量(一定),所以平均每天用去的千克数和用的天数成反比例;
故答案为:D
4.D
【分析】根据x÷y=k(一定),x和y成正比例关系,进行分析。
【详解】A.=3y,3xy=1,xy=,x和y不成正比例;
B.(x+1)y=1,xy+y=1,x和y不成比例;
C.x+y=13,x和y之间有和的关系,不成比例;
D.y=8x,x=y,x÷y=,x和y成正比例关系;
故答案为:D
5.B
【分析】设乙每年缴纳养老保险为x万元,则甲每年缴纳养老保险金为(x+0.2)万元,根据甲、乙两人计划用相同的年数分别缴纳养老保险金18万元和12万元可知,18比上(x+0.2)万元等于12比上x万元。
【详解】根据题意可列出比例为。
故答案为:B
6.A
【分析】由题意可得:甲数×=乙数×,逆运用比例的基本性质,即可写出这个比例式。
【详解】甲数×=乙数×
得甲∶乙=∶=9∶4
故答案为:A
【点睛】此题主要考查比例的基本性质的灵活应用,掌握比例性质:两外项积等于两内项积是解题关键。
7.比例的基本性质
【分析】在比例中,20和x是两个外项,25和4是两个内项,根据比例的基本性质,写成两个外项的积等于两个内项的积的形式,再根据等式的性质解出比例。
【详解】由分析可得:解比例20∶25=4∶x的第一步是:20x=25×4,这一步利用了比例的基本性质。
8. 正
【分析】根据题意,可先将改写成7m=5n,然后等式两边同时除以7,除以n,即可通过转化得出m和n的比。或根据比例的基本性质直接得到。根据x÷y=k(一定),x和y成正比例关系,即可确定m和n的比例关系。
【详解】由可得7m=5n
7m÷7÷n=5n÷7÷n
m÷n=5÷7=
所以,m∶n=5∶7,m和n成正比例关系。
9.9∶8
【分析】根据题意,松树×=杨树×,逆运用比例的基本性质,即可求出松树与杨树的棵数比。
【详解】因为松树×=杨树×,
所以,松树∶杨树=∶=(×12)∶(×12)=9∶8,
所以,松树棵数的等于杨树棵数的,则松树与杨树的棵数比是9∶8。
【点睛】本题考查了比例的基本性质,两内项之积等于两外项之积。
10.22.5
【分析】观察题意可知,图中的折线是一条直线,说明这是个正比例图像,水的体积÷注水时间=每分钟注入水的体积(一定),水的体积和注水时间的比值一定,则它们成正比例;已知5分钟注水10升,用10÷5即可求出每分钟注入水的体积,然后再根据水的体积÷每分钟注入水的体积=注水时间,代入数据即可求出注水时间。
【详解】观察图可知,5分钟注水10升,
10÷5=2(升)
45÷2=22.5(分)
若箱内水的体积是45升,则注水22.5分钟。
【点睛】本题主要考查了正比例的意义和辨识,掌握相关的图像是解答本题的关键。
11.12.8
【分析】设旗杆实际高为x米,根据竹高∶影长=旗杆高∶影长,列出比例求出x的值即可。
【详解】解:这旗杆实际高为x米。
0.6∶1.2=x∶25.6
1.2x÷1.2=15.36÷1.2
x=12.8
【点睛】用比例解决问题,只要左右两边的比统一即可。
12. 每行站的人数 站的行数 反
【分析】判断两种相关联的量成不成比例,成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,就成反比例,如果是其它的量一定或乘积、比值不一定,就不成比例;据此解答。
【详解】由题意可知:每行站的人数×站的行数=六年级总人数(一定),即每行站的人数和站的行数的乘积一定,所以每行站的人数和站的行数成反比例关系。
【点睛】本题主要考查辨识成正比例的量和成反比例的量。
13.×
【分析】根据比例的基本性质,比例的两内项积=两外项积,进行分析。
【详解】如果a∶b=x∶y,可得bx=ay,原题说法错误。
故答案为:×
14.×
【分析】先根据比例的基本性质,把改写成比例是a∶b=∶;再根据比的基本性质,把∶化成最简整数比。
【详解】因为a作外项,所以作外项;因为b作内项,所以作内项。即由可推导出:a∶b=∶。
∶=(×6)∶(×6)=3∶4。
所以a∶b=3∶4。即原题说法错误。
故答案为:×
【点睛】把等式ax=by改写成比例时(a,b,x,y均不为0),相乘的2个字母必须同时作比例的外项或内项。
15.×
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。据此解答。
【详解】用方砖给一间教室铺地面,这间教室的总面积一定,相当于方砖的面积与用砖的块数的乘积是一定的,那么方砖的面积与用砖的块数是成反比例的,所以原题的说法是错误的。
故答案为:×
【点睛】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
16.√
【分析】采用赋值法,假设a=3,那么等式左边就等于1,那么右边也等于1,则b=5,这样就能判断a与b的大小关系。
【详解】如果a=3,那么b=5,所以a一定小于b,所以原题正确。
故答案为:√
【点睛】本题的解题关键是假设等于一个确切的数字,然后分别求出a和b,然后比较大小。
17.×
【分析】根据题意黑兔只数比白兔只数少20%,所以白兔只数×(1-20%)=黑兔只数,所以=(1-20%)(一定),白兔只数和黑兔只数的比值一定,所以成正比例。
【详解】黑兔只数比白兔只数少20%,黑兔只数与白兔只数的比值一定,成正比例。
故答案为:×
【点睛】本题考查正反比例的定义,两个相关量的比值一定成正比例,两个相关的量积一定成反比例。
18.;;
【分析】,先将左边合并成1.25x,根据等式的性质2,两边同时÷1.25即可;
,根据比例的基本性质,先写成的形式,根据等式的性质2,两边同时÷即可;
,根据等式的性质,先写成的形式,根据等式的性质2,两边同时÷3即可。
【详解】
解:
解:
解:
19.71.4千克
【分析】由题意可知,设爸爸的体重是x千克,根据体重与船下沉的高度的比值一定,可确定体重与下沉的高度成正比例,据此可列比例解答即可。
【详解】解:设爸爸的体重是x千克。
35.7∶2=x∶4
2x=35.7×4
2x=142.8
2x÷2=142.8÷2
x=71.4
答:爸爸的体重是71.4千克。
20.7天
【分析】由题意可知,设看完这本书还需用x天,因为每天看的页数是一定的,则看的页数和天数成正比例,据此列比例解答即可。
【详解】解:设看完这本书还需x天。
45x=105×3
45x=315
45x÷45=315÷45
x=7
答:照这样的速度,看完这本书还需用7天。
【点睛】本题考查用比例解决实际问题,明确看的页数和天数成正比例是解题的关键。
21.9小时
【分析】由题意可知,设需要x个小时才能到达,因为中巴客车的速度不变,则路程和时间成正比例,据此列比例解答即可。
【详解】解:设需要x小时才能到达。
120∶2=540∶x
120x=540×2
120x=1080
120x÷120=1080÷120
x=9
答:需要9小时才能到达。
【点睛】本题考查用比例解决实际问题,明确路程和时间成正比例是解题的关键。
22.225块
【分析】根据题意可知,每块方砖的面积×块数=地面的面积(一定),所以每块方砖的面积和块数成反比例,根据正方形的面积公式,设用边长是0.8米的方砖铺地,需要x块,列方程为0.8×0.8×x=0.6×0.6×400,然后解出方程即可。
【详解】解:用边长是0.8米的方砖铺地,需要x块。
0.8×0.8×x=0.6×0.6×400
0.64x=144
x=144÷0.64
x=225
答:用边长是0.8米的方砖铺地,需要225块。
【点睛】本题主要考查了反比例的应用,明确相关的量是正比例还是反比例是解答本题的关键。
23.路程和时间成正比例;从济南到郑州需要5.5小时
【分析】根据正比例意义:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数比值一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系。可以判断路程和时间成正比例关系,再解设未知量,根据“速度一定”列出比例,进而利用比例的基本性质求解。
【详解】因为速度(一定),所以路程和时间成正比例。
解:设从济南到郑州需要个小时,
答:从济南到郑州需要5.5小时。
【点睛】此题考查对正比例意义的理解,以及用列比例解决问题的方法和步骤。
24.640毫升
【分析】用酒精的含量∶酒精溶液=19∶20,即酒精的含量∶2400=19∶20,求出酒精的含量;根据题意可知,酒精的含量不变,再用求出的酒精的含量:酒精溶液=3∶4,求出配制75%的酒精时的酒精溶液量,再减去原来的2400毫升即可求出加水量。
【详解】解:设酒精的含量为x毫升;设配制75%的酒精时的酒精溶液量为y毫升;
x∶2400=19∶20
20 x=2400×19
x=2280;
2280∶y=3∶4
3y=2280×4
y=3040;
3040-2400=640(毫升)
答:需要加水640毫升。
【点睛】明确酒精的含量不变是解答本题的关键,进而求出配制75%的酒精时的酒精溶液量,再进一步解答。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第3单元比例易错精选题-数学六年级下册青岛版
一、选择题
1.解比例的依据是( )。
A.等式的基本性质 B.比的基本性质
C.比例的基本性质 D.比例的定义
2.下列选项中的两个量,成正比例关系的是( )。
A.圆柱的体积和底面积 B.一个人的身高和年龄
C.圆的周长和半径 D.飞机从北京飞往上海的速度和时间
3.下面各数量关系中,成反比例关系的是( )。
A.全班人数一定,缺勤人数和出勤人数 B.三角形的高一定,它的面积和底
C.正方形的边长和面积 D.一桶油,平均每天用去的千克数和用的天数
4.如果( ),那么x和成正比例(x、y均不为0)。
A. B. C. D.
5.我国逐渐完善养老金制度,居民可自行缴纳养老金。甲、乙两人计划用相同的年数分别缴纳养老金18万元和12万元。甲计划每年比乙多缴纳保险金0.2万元。若乙每年缴纳保险金x万元,则根据题意可列出比例为( )。
A. B.
C. D.
6.甲乙两个数均大于0,若甲的等于乙的,则甲、乙两数的比是( )。
A.9∶4 B.4∶1 C.3∶1 D.4∶3
二、填空题
7.解比例20∶25=4∶x的第一步是:20x=25×4,这一步利用了( )。
8.如果(m、n都不为0),那么( ),m和n成( )比例。
9.松树棵数的等于杨树棵数的,则松树与杨树的棵数比是( )。
10.如图,一根水管不停地向水箱注水,箱内水的体积不断变化。若箱内水的体积是45升,则注水( )分钟。
11.小明在同一时刻测量了操场上直立在太阳下两根竹竿的长度和影子长,如表。在这一时刻小明又测得了直立的旗杆影长为25.6米,旗杆实际高为( )米。
竹高(米) 0.6 0.8
影长(米) 1.2 1.6
12.六年级同学做广播操,每行站20人,正好站12行。如果每行站16人,能站多少行?此题中,( )和( )成( )比例关系。
三、判断题
13.如果a∶b=x∶y,则ax=by。( )
14.如果(a和b都不等于0),那么。( )
15.用方砖给一间教室铺地面,方砖的边长与用砖的块数成反比例。( )
16.a和b是两个不同的非0自然数,如果,那么a一定小于b。( )
17.黑兔只数比白兔只数少20%,黑兔只数与白兔只数成反比例。( )
四、计算题
18.解方程。
五、解答题
19.淘气模仿“曹冲称象”来称体重。淘气站在船上,船下沉2厘米;爸爸站在船上,船下沉4厘米。淘气的体重是35.7千克,爸爸的体重是多少千克?
20.一本故事书共150页,李丽3天看了45页,照这样的速度,看完这本书还需用多少天?(用比例解)
21.一辆中巴客车从甲地开往乙地,2小时行了120千米。照这样的速度,从聊城到烟台共540千米,需要几小时才能到达?(用比例解)
22.学校创客室的地面是正方形的,用边长是0.6米的方砖铺地,正好需要400块。如果改用边长是0.8米的方砖铺地,需要多少块?(用比例方法解荅)
23.科技的发展改善了我们的生活,也改变了人们的出行方式,人们可以选择的交通工具多种多样,如:地铁、汽车、高铁、火车、飞机等。据了解,从济南到郑州的公路长是440km。若一辆车2小时行了160km,照这样计算,从济南到郑州需要多少个小时?先说说路程和时间成什么比例,再用比例解。
24.抗击新冠肺炎期间,爷爷需要配制75%的酒精消毒,然而家里只有95%的酒精2400ml。小明利用本学期刚学过的相关知识,决心帮爷爷把家里95%的酒精稀释成75%,需要加水多少毫升的问题。
小明操作如下:
(1)把75%的酒精转化为:酒精与酒精溶液的比是3∶4。
(2)把95%的酒精转化为:酒精与酒精溶液的比19∶20。
接下来,请你帮小明算一算,需要加水多少毫升?
参考答案:
1.C
【分析】如果已经知道比例中的任意三项,根据比例的基本性质,可以求出比例中另一个未知项。求比例中的未知项,叫做解比例。
【详解】解比例的依据是比例的基本性质,即比例的两内项积=两外项积。
故答案为:C
2.C
【分析】根据x÷y=k(一定),x和y成正比例关系;xy=k(一定),x和y成反比例关系,进行分析。
【详解】A.圆柱的体积÷底面积=高,不确定高是否一定,无法确定圆柱的体积和底面积是否成正比例关系;
B.一个人的身高和年龄不成比例关系;
C.圆的周长÷半径=圆周率×2,圆的周长和半径成正比例关系;
D.北京到上海的距离一定,速度×时间=路程,飞机从北京飞往上海的速度和时间成反比例关系。
成正比例关系的是圆的周长和半径。
故答案为:C
3.D
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例;如果是其它的量一定或乘积、比值不一定,就不成比例。据此解答即可。
【详解】A.出勤人数+缺勤人数=总人数,总人数一定,出勤人数和缺勤人数不成比例关系;
B.因为三角形的面积=底×高×,所以三角形的面积÷底=高×(一定),符合x÷y=k(一定),所以三角形的高一定,它的面积和底成正比例;
C.正方形的面积=边长×边长,在这个关系中,边长发生变化,正方形的面积也发生变化,而正方形的另一个边长也随着发生了变化,三个量都是变化的,没有一定的量,所以正方形的边长和面积不成比例;
D.每天用的千克数×所用的天数=这桶油的质量(一定),所以平均每天用去的千克数和用的天数成反比例;
故答案为:D
4.D
【分析】根据x÷y=k(一定),x和y成正比例关系,进行分析。
【详解】A.=3y,3xy=1,xy=,x和y不成正比例;
B.(x+1)y=1,xy+y=1,x和y不成比例;
C.x+y=13,x和y之间有和的关系,不成比例;
D.y=8x,x=y,x÷y=,x和y成正比例关系;
故答案为:D
5.B
【分析】设乙每年缴纳养老保险为x万元,则甲每年缴纳养老保险金为(x+0.2)万元,根据甲、乙两人计划用相同的年数分别缴纳养老保险金18万元和12万元可知,18比上(x+0.2)万元等于12比上x万元。
【详解】根据题意可列出比例为。
故答案为:B
6.A
【分析】由题意可得:甲数×=乙数×,逆运用比例的基本性质,即可写出这个比例式。
【详解】甲数×=乙数×
得甲∶乙=∶=9∶4
故答案为:A
【点睛】此题主要考查比例的基本性质的灵活应用,掌握比例性质:两外项积等于两内项积是解题关键。
7.比例的基本性质
【分析】在比例中,20和x是两个外项,25和4是两个内项,根据比例的基本性质,写成两个外项的积等于两个内项的积的形式,再根据等式的性质解出比例。
【详解】由分析可得:解比例20∶25=4∶x的第一步是:20x=25×4,这一步利用了比例的基本性质。
8. 正
【分析】根据题意,可先将改写成7m=5n,然后等式两边同时除以7,除以n,即可通过转化得出m和n的比。或根据比例的基本性质直接得到。根据x÷y=k(一定),x和y成正比例关系,即可确定m和n的比例关系。
【详解】由可得7m=5n
7m÷7÷n=5n÷7÷n
m÷n=5÷7=
所以,m∶n=5∶7,m和n成正比例关系。
9.9∶8
【分析】根据题意,松树×=杨树×,逆运用比例的基本性质,即可求出松树与杨树的棵数比。
【详解】因为松树×=杨树×,
所以,松树∶杨树=∶=(×12)∶(×12)=9∶8,
所以,松树棵数的等于杨树棵数的,则松树与杨树的棵数比是9∶8。
【点睛】本题考查了比例的基本性质,两内项之积等于两外项之积。
10.22.5
【分析】观察题意可知,图中的折线是一条直线,说明这是个正比例图像,水的体积÷注水时间=每分钟注入水的体积(一定),水的体积和注水时间的比值一定,则它们成正比例;已知5分钟注水10升,用10÷5即可求出每分钟注入水的体积,然后再根据水的体积÷每分钟注入水的体积=注水时间,代入数据即可求出注水时间。
【详解】观察图可知,5分钟注水10升,
10÷5=2(升)
45÷2=22.5(分)
若箱内水的体积是45升,则注水22.5分钟。
【点睛】本题主要考查了正比例的意义和辨识,掌握相关的图像是解答本题的关键。
11.12.8
【分析】设旗杆实际高为x米,根据竹高∶影长=旗杆高∶影长,列出比例求出x的值即可。
【详解】解:这旗杆实际高为x米。
0.6∶1.2=x∶25.6
1.2x÷1.2=15.36÷1.2
x=12.8
【点睛】用比例解决问题,只要左右两边的比统一即可。
12. 每行站的人数 站的行数 反
【分析】判断两种相关联的量成不成比例,成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,就成反比例,如果是其它的量一定或乘积、比值不一定,就不成比例;据此解答。
【详解】由题意可知:每行站的人数×站的行数=六年级总人数(一定),即每行站的人数和站的行数的乘积一定,所以每行站的人数和站的行数成反比例关系。
【点睛】本题主要考查辨识成正比例的量和成反比例的量。
13.×
【分析】根据比例的基本性质,比例的两内项积=两外项积,进行分析。
【详解】如果a∶b=x∶y,可得bx=ay,原题说法错误。
故答案为:×
14.×
【分析】先根据比例的基本性质,把改写成比例是a∶b=∶;再根据比的基本性质,把∶化成最简整数比。
【详解】因为a作外项,所以作外项;因为b作内项,所以作内项。即由可推导出:a∶b=∶。
∶=(×6)∶(×6)=3∶4。
所以a∶b=3∶4。即原题说法错误。
故答案为:×
【点睛】把等式ax=by改写成比例时(a,b,x,y均不为0),相乘的2个字母必须同时作比例的外项或内项。
15.×
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。据此解答。
【详解】用方砖给一间教室铺地面,这间教室的总面积一定,相当于方砖的面积与用砖的块数的乘积是一定的,那么方砖的面积与用砖的块数是成反比例的,所以原题的说法是错误的。
故答案为:×
【点睛】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
16.√
【分析】采用赋值法,假设a=3,那么等式左边就等于1,那么右边也等于1,则b=5,这样就能判断a与b的大小关系。
【详解】如果a=3,那么b=5,所以a一定小于b,所以原题正确。
故答案为:√
【点睛】本题的解题关键是假设等于一个确切的数字,然后分别求出a和b,然后比较大小。
17.×
【分析】根据题意黑兔只数比白兔只数少20%,所以白兔只数×(1-20%)=黑兔只数,所以=(1-20%)(一定),白兔只数和黑兔只数的比值一定,所以成正比例。
【详解】黑兔只数比白兔只数少20%,黑兔只数与白兔只数的比值一定,成正比例。
故答案为:×
【点睛】本题考查正反比例的定义,两个相关量的比值一定成正比例,两个相关的量积一定成反比例。
18.;;
【分析】,先将左边合并成1.25x,根据等式的性质2,两边同时÷1.25即可;
,根据比例的基本性质,先写成的形式,根据等式的性质2,两边同时÷即可;
,根据等式的性质,先写成的形式,根据等式的性质2,两边同时÷3即可。
【详解】
解:
解:
解:
19.71.4千克
【分析】由题意可知,设爸爸的体重是x千克,根据体重与船下沉的高度的比值一定,可确定体重与下沉的高度成正比例,据此可列比例解答即可。
【详解】解:设爸爸的体重是x千克。
35.7∶2=x∶4
2x=35.7×4
2x=142.8
2x÷2=142.8÷2
x=71.4
答:爸爸的体重是71.4千克。
20.7天
【分析】由题意可知,设看完这本书还需用x天,因为每天看的页数是一定的,则看的页数和天数成正比例,据此列比例解答即可。
【详解】解:设看完这本书还需x天。
45x=105×3
45x=315
45x÷45=315÷45
x=7
答:照这样的速度,看完这本书还需用7天。
【点睛】本题考查用比例解决实际问题,明确看的页数和天数成正比例是解题的关键。
21.9小时
【分析】由题意可知,设需要x个小时才能到达,因为中巴客车的速度不变,则路程和时间成正比例,据此列比例解答即可。
【详解】解:设需要x小时才能到达。
120∶2=540∶x
120x=540×2
120x=1080
120x÷120=1080÷120
x=9
答:需要9小时才能到达。
【点睛】本题考查用比例解决实际问题,明确路程和时间成正比例是解题的关键。
22.225块
【分析】根据题意可知,每块方砖的面积×块数=地面的面积(一定),所以每块方砖的面积和块数成反比例,根据正方形的面积公式,设用边长是0.8米的方砖铺地,需要x块,列方程为0.8×0.8×x=0.6×0.6×400,然后解出方程即可。
【详解】解:用边长是0.8米的方砖铺地,需要x块。
0.8×0.8×x=0.6×0.6×400
0.64x=144
x=144÷0.64
x=225
答:用边长是0.8米的方砖铺地,需要225块。
【点睛】本题主要考查了反比例的应用,明确相关的量是正比例还是反比例是解答本题的关键。
23.路程和时间成正比例;从济南到郑州需要5.5小时
【分析】根据正比例意义:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数比值一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系。可以判断路程和时间成正比例关系,再解设未知量,根据“速度一定”列出比例,进而利用比例的基本性质求解。
【详解】因为速度(一定),所以路程和时间成正比例。
解:设从济南到郑州需要个小时,
答:从济南到郑州需要5.5小时。
【点睛】此题考查对正比例意义的理解,以及用列比例解决问题的方法和步骤。
24.640毫升
【分析】用酒精的含量∶酒精溶液=19∶20,即酒精的含量∶2400=19∶20,求出酒精的含量;根据题意可知,酒精的含量不变,再用求出的酒精的含量:酒精溶液=3∶4,求出配制75%的酒精时的酒精溶液量,再减去原来的2400毫升即可求出加水量。
【详解】解:设酒精的含量为x毫升;设配制75%的酒精时的酒精溶液量为y毫升;
x∶2400=19∶20
20 x=2400×19
x=2280;
2280∶y=3∶4
3y=2280×4
y=3040;
3040-2400=640(毫升)
答:需要加水640毫升。
【点睛】明确酒精的含量不变是解答本题的关键,进而求出配制75%的酒精时的酒精溶液量,再进一步解答。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
