圆柱与圆锥专题突破-数学六年级下册北师大版(含解析)
文档属性
| 名称 | 圆柱与圆锥专题突破-数学六年级下册北师大版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 397.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-24 19:21:14 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
圆柱与圆锥专题突破-数学六年级下册北师大版
1.给大厅中一根圆柱形立柱刷漆。已知立柱高4米,底面半径是0.5米,每平方米需油漆0.4千克。将这根立柱全部刷完共需多少千克油漆?
2.一个圆柱茶叶筒的侧面积是188.4平方厘米,底面直径是6厘米。它的高是多少厘米?
3.一个圆柱的侧面展开图恰好是一个边长为18.84厘米的正方形,求这个圆柱体的表面积。
4.把一个底面半径是3分米,长是9分米的圆柱形木头锯成长短不同的五小段圆柱形木头,表面积增加了多少平方分米?
5.芳芳正在制作圆柱,她用下面这张长方形纸做圆柱的侧面,再用其他的纸做上下底面,就可以粘成一个圆柱制作的过程中她发现可以做出两个不同的圆柱,她认为围成的两个不同的圆柱的表面积是相同的,你同意吗?把你的思考过程写一写。取
6.一个圆柱形水池,底面周长是31.4米,深是3米,在池底及池壁抹一层水泥,抹水泥的面积是多少平方米?
7.妙想家经常用一种空心圆柱形状的卷纸(如图),测得这种卷纸的底面外直径是12厘米,内直径是6厘米,高是10厘米。若要给这种卷纸的内、外侧和上、下底面包上一层塑料膜,至少需要多少平方厘米的塑料膜?
8.把一个底面半径为5分米、高为9.6分米的圆锥形零件,改铸成底面直径为8分米的圆柱形零件,铸成的圆柱形零件的高是多少分米?
9.一个圆锥形零件,它的底面半径是5cm.高是底面半径的3倍,这个零件的体积是多少立方厘米?
10.一个圆柱体侧面展开后是一个长6.28厘米,宽3.14厘米的长方形,底面直径是多少厘米?如果把它削成一个最大的圆锥,削去部分的体积是多少?
11.一个底面半径是8cm的圆柱形玻璃器皿装满了水,水中浸着一个底面半径是4cm的圆锥形铅锤,当铅锤从水中取出后,水面下降了2cm.这个铅锤的体积是多少?
12.一个圆柱和一个圆锥等底等高,它们的体积和是50.24立方分米,如果圆锥的底面半径是2分米,这个圆锥的高是多少分米?
13.一个直角三角形的三条边分别为3厘米、4厘米、5厘米,沿它的一条直角边为轴旋转一周,可得什么图形?体积最小是多少?体积最大是多少?
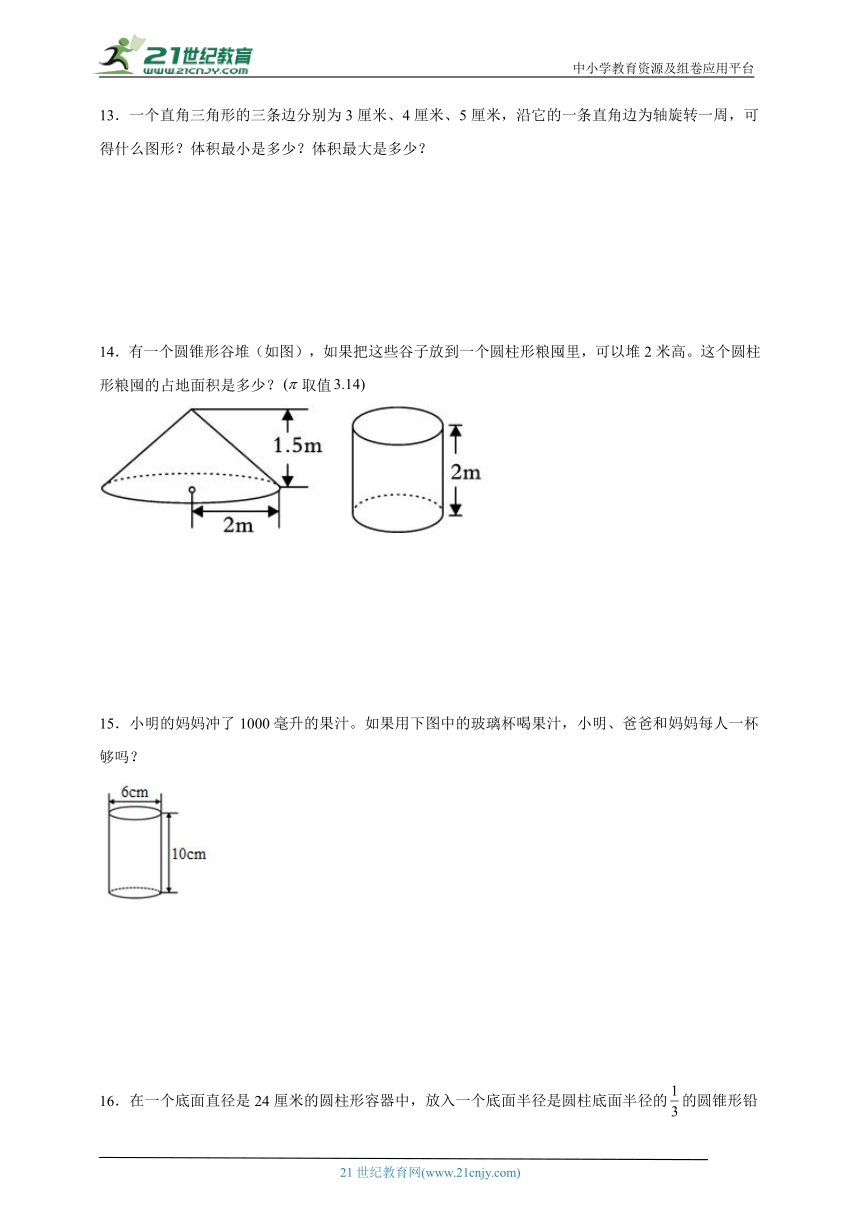
14.有一个圆锥形谷堆(如图),如果把这些谷子放到一个圆柱形粮囤里,可以堆2米高。这个圆柱形粮囤的占地面积是多少?取值
15.小明的妈妈冲了1000毫升的果汁。如果用下图中的玻璃杯喝果汁,小明、爸爸和妈妈每人一杯够吗?
16.在一个底面直径是24厘米的圆柱形容器中,放入一个底面半径是圆柱底面半径的的圆锥形铅锤后,再注满水。当铅锤从水中取出后,水面下降了0.5厘米,铅锤的高是多少厘米?
17.一根圆柱形木料的高是25分米,底面直径比高少,这根木料的表面积是多少平方分米?
18.把一个底面半径是6厘米,高比底面半径多的圆柱形铁块熔铸成一个底面半径是圆柱底面半径的的圆锥形铁块,熔铸成的圆锥形铁块的高是多少厘米?
19.一个长方体橡皮泥如下图:
(1)如果把它捏成同样高的圆锥,这个圆锥的底面积是多少?
(2)如果把这个长方体橡皮泥捏成底面积是15平方厘米的圆柱,这个圆柱的高是多少厘米?
20.爸爸的茶杯(如图)。
(1)小红怕烫伤爸爸的手,特意在茶杯上贴了一个装饰带,这个装饰带的面积是多少?
(2)这个茶杯的容积大约是多少毫升?(玻璃的厚度忽略不计)
21.一个直径是8cm的瓶子里,水的高度是12cm,把瓶盖拧紧倒置放平,无水部分是圆柱形,高度是8cm,这个瓶子的容积是多少?(厚度忽略不计)
22.冬奥会项目设有单板滑香U形池赛,张叔叔根据单板滑雪U形池制作了一个U形池的简化模型(如图),形状可以看为一个长方体中挖去了半个圆柱体(沿高平分)。已知该模型的长为15分米,宽为6分米,高为3分米,其中挖圆柱体的底面直径为4分米。该模型的体积是多少立方分米?
参考答案:
1.5.024千克
【分析】根据题意可知,给圆柱形立柱刷漆,只是刷侧面,底面与顶面不用刷,故根据圆柱侧面积公式:,求出侧面积再乘0.4即可解答。
【详解】2×3.14×0.5×4×0.4
=3.14×4×0.4
=5.024(千克)
答:将这根立柱全部刷完共需5.024千克油漆。
【点睛】此题主要考查学生对圆柱侧面积的理解与求取方法,需要理解给圆柱形立柱刷漆,只是刷侧面,底面与顶面不用刷。
2.10cm
【分析】根据圆柱的侧面积公式:S=πdh,得出h=S÷(πd),代入数据计算即可
【详解】188.4÷(3.14×6)
=188.4÷18.84
=10(cm)
答:它的高是10厘米。
【点睛】本题考查圆柱侧面积公式的逆运用,牢记圆柱的侧面积公式是解题的关键。
3.411.4656平方厘米
【详解】18.84÷3.14÷2=3(厘米)
3.14×32×2+18.84×18.84=411.4656(平方厘米)
4.226.08平方分米
【分析】锯圆柱形木头,表面积增加的部分是若干个相同的底面积.锯成五段,要锯4次,每锯一次增加两个面,锯了4次增加了八个面.
【详解】3.14 × 3 × 8 = 226.08(平方分米)
5.见详解
【分析】由圆柱的侧面展开图的特点可知:圆柱的侧面展开后,是一个长方形,可以先把长方形的长当作底面周长,宽就是圆柱的高,也可以把长方形的宽当作圆柱的底面周长,长就是圆柱的高,求出底面半径,再比较选择即可。
【详解】不同意;因为圆柱的表面积=侧面积个底面积,两个不同的圆柱,侧面积都相等,都等于这个长方形的面积,所以,只要比较底面积即可,底面半径越大,底面积就越大,所以比较半径即可。
18.84÷3.14÷2
=6÷2
=3(cm)
12.56÷3.14÷2
=4÷2
=2(cm)
所以,底面积不同,由此围成的两个不同的圆柱的表面积也是不相同的。
【点睛】解答此题的关键是明白:圆柱的侧面展开后,是一个长方形,反过来,可以把长方形的长当作底面周长,宽等于圆柱的高,也可以把宽当作底面周长,长当作圆柱的高。
6.172.7平方米
【分析】抹水泥的面积为圆柱的侧面积与一个底面积的和,根据侧面积=底面周长×高,底面积=半径×半径×圆周率,将相关数据代入即可解答。
【详解】水池的侧面积:31.4×3=94.2(平方米)
水池的底面积:
3.14×(31.4÷3.14÷2)2
=3.14×52
=3.14×25
=78.5(平方米)
抹水泥部分的面积是:94.2+78.5=172.7(平方米)
答:抹水泥部分的面积是172.7平方米。
【点睛】此题主要考查圆柱表面积公式在实际生活中的应用,关键是熟记公式。
7.734.76平方厘米
【分析】观察题意可知,塑料膜的面积=内侧面积+外侧面积+上、下底的圆环面积,根据圆柱的侧面积公式:S=πdh,用3.14×12×10+3.14×6×10即可求出内外侧的面积和,再根据圆环面积公式:S=π(R2-r2),用3.14×[(12÷2)2-(6÷2)2]×2即可求出上下底的面积,最后把内外侧的面积和加上上下底的面积,即可求出塑料膜的面积。
【详解】3.14×12×10+3.14×6×10
=376.8+188.4
=565.2(平方厘米)
3.14×[(12÷2)2-(6÷2)2] ×2
=3.14×[62-32] ×2
=3.14×[36-9] ×2
=3.14×27×2
=169.56(平方厘米)
565.2+169.56=734.76(平方厘米)
答:至少需要734.76平方厘米的塑料膜。
【点睛】本题主要考查了圆柱侧面积公式以及底面积公式的灵活应用,要注意表面由哪些面组成。
8.5分米
【详解】试题分析:根据题意可知,圆锥钢材的体积等于铸造成的圆柱零件的体积,可先根据圆锥的体积公式求出这个零件的体积,再利用圆柱的高=体积×3÷底面积即可解答.
解:(3.14×52×9.6×)÷[3.14×(8÷2)2]
=251.2÷50.24,
=5(分米),
答:铸成的圆柱形零件的高是5分米.
点评:解答此题的关键是确定圆锥形钢材的体积等于铸造成的圆柱形零件的体积,然后再根据圆锥的体积公式和圆柱的体积公式进行计算即可.
9.392.5立方厘米
【详解】试题分析:根据“底面半径是5dm,高是底面半径的3倍可求出高,再根据圆锥的体积公式,V=Sh,列式解答即可.
解:×3.14×52×(5×3)
=×3.14×25×15,
=392.5(立方厘米);
答:这个零件的体积是392.5立方厘米.
点评:本题主要考查圆锥的体积计算,要牢记圆锥的体积公式V=Sh,不能忘记乘.
10.6.57立方厘米
【详解】试题分析:由圆柱的侧面展开图的特点可知:圆柱的侧面展开得到的是一个长方形,长方形的长等于圆柱底面周长,宽等于圆柱的高;由此根据圆的周长公式,求出这个圆柱体的底面直径.根据圆柱的体积公式:v=sh,把数据代入公式解答;如果把它削成一个最大的圆锥,这个圆锥与圆柱等底等高,因为等底等高的圆锥的体积是圆柱体积的,所以削去部分的体积是圆柱体积的(1),然后根据一个数乘分数的意义解答.
解:底面直径是:6.28÷3.14=2(厘米);
3.14×()2×3.14×(1),
=3.14×1×3.14×,
=9.8596×,
=,
≈6.57(立方厘米);
答:圆柱的底面直径是2厘米,削去部分的体积约是6.57立方厘米.
点评:此题考查的目的是掌握圆柱的侧面展开的特点,以及圆柱体积的计算.
11.401.92立方厘米
【详解】试题分析:圆锥形铅锤的体积就是铅锤从水中取出后,水面下降了2cm,下降的水的体积就是铅锤的体积.下降的这部分水的形状是一个底面半径是8cm的圆柱形,因此求出这个圆柱的体积即可.
解:3.14×82×2,
=3.14×128,
=401.92(立方厘米);
答:这个铅锤的体积是401.92立方厘米
点评:本题考查了圆柱的体积公式的运用,同时考查了学生的转化思想,下降水的体积就是铅锤体积.
12.3分米
【详解】试题分析:根据等底等高的圆柱的体积是圆锥的体积的3倍,把圆锥的体积看作1份,圆柱的体积是3份,它们的和是(1+3)份,由此再根据“它们的体积之和是50.24立方分米”,求出圆锥的体积,再利用圆锥的体积公式求出它的高即可.
解:50.24÷4=12.56(立方分米),
3.14×22=12.56(平方分米),
12.56×3÷12.56=3(分米),
答:圆锥的高是3分米.
点评:此题主要考查了等底等高的圆柱的体积与圆锥的体积的关系,解答时注意找准50.24立方分米的对应倍数.
13.绕着它的任意一条直角边旋转一周可以得到一个圆锥体,这个图形的体积最小是37.68立方厘米,最大是50.24立方厘米
【详解】试题分析:直角三角形绕一条直角边旋转一周,得到的图形是一个圆锥体,由此可知:(1)以4厘米直角边为轴旋转,得到的是底面半径为3厘米,高为4厘米的圆锥;(2)以3厘米的直角边为轴旋转,得到的是一个底面半径为4厘米,高为3厘米的圆锥,由此利用圆锥的体积公式求出它们的体积即可解答.
解::(1)以4厘米直角边为轴旋转,得到的是底面半径为3厘米,高为4厘米的圆锥;
体积为:×3.14×32×4,
=×3.14×9×4,
=37.68(立方厘米);
(2)以3厘米的直角边为轴旋转,得到的是一个底面半径为4厘米,高为3厘米的圆锥,
体积是:×3.14×42×3,
=3.14×16,
=50.24(立方厘米),
答:绕着它的任意一条直角边旋转一周可以得到一个圆锥体,这个图形的体积最小是37.68立方厘米,最大是50.24立方厘米.
点评:此题考查圆锥的体积公式的计算应用,抓住圆锥的展开图的特点,得出直角三角形绕直角边旋转一周得出的是圆锥体是解决本题的关键.
14.3.14平方米
【分析】根据圆锥的体积公式:体积=底面积×高×,代入数据,求出圆锥的体积;圆锥的体积等于高是2米的圆柱的体积,根据圆柱的体积公式:体积=底面积×高;底面积=体积÷高,代入数据,即可解答。
【详解】3.14×22×1.5×÷2
=3.14×4×1.5×÷2
=12.56×1.5×÷2
=18.84×÷2
=6.28÷2
=3.14(平方米)
答:这个圆柱形粮囤的占地面积是3.14平方米。
【点睛】熟练掌握和灵活运用圆柱的体积公式和圆锥的体积公式是解答本题的关键。
15.够
【分析】根据圆柱的体积公式:体积=底面积×高,代入数据,求出玻璃杯的体积,再求出3倍果汁的体积,再和1000毫升比较,如果3倍果汁的体积大于1000毫升,就不够每人一杯;如果3杯果汁的体积小于1000毫升,就够每人一杯,据此解答。
【详解】3.14×(6÷2)2×10
=3.14×9×10
=28.26×10
=282.6(立方厘米)
282.6立方厘米=282.6毫升
282.6×3=847.8(毫升)
847.8<1000,小明、爸爸和妈妈每人一杯够。
答:小明、爸爸和妈妈每人一杯够。
【点睛】熟练掌握圆柱的体积公式以及单位名数的换算是解答本题的关键。
16.3.375厘米
【分析】当铅锤从水中取出后,水面下降的体积就是这个铅锤的体积;根据直径与半径的关系可求出这个圆柱形容器的底面半径,根据圆柱的体积计算公式即可求出水面下降的体积,即铅锤的体积;根据直径与半径的关系可求出圆锥形铅锤,再根据圆锥的体积计算公式“V=r2h”即可求出铅锤高。
【详解】24×=8(厘米)
3.14×()2×0.5×3÷(3.14×82)
=3.14×122×0.5×3÷(3.14×64)
=3.14×144×0.5×3÷(3.14×64)
=678.24÷200.96
=3.375(厘米)
答:铅锤高3.375厘米。
【点睛】此题是考查圆柱、圆锥体积的计算,关键是圆锥体积公式的灵活运用。
17.339.12平方分米
【分析】把故看作单位“1”,根据求一个数的几分之几是多少,用乘法求出底面直径,再根据圆柱的表面积=侧面积+底面积×2,圆柱的侧面积=底面周长×高,圆的面积公式:S=πr2,把数据代入公式解答。
【详解】25×(1-)
=25×
=4(分米)
3.14×4×25+3.14×(4÷2)2×2
=12.56×25+3.14×4×2
=314+25.12
=339.12(平方分米)
答:这个圆柱的表面积是339.12平方分米。
【点睛】此题主要考查圆柱表面积公式的灵活运用,关键是熟记公式。
18.54厘米
【分析】把底面半径看作单位“1”,高是半径的(1+),用半径×(1+),求出圆柱的底面半径;再根据圆柱的体积公式:体积=底面积×高,代入数据,求出圆柱的体积;圆柱铸成圆锥,圆柱的体积等于圆锥的体积;把圆柱的半径看作单位“1”,用圆柱的半径×,代入数据,求出圆锥的半径,再根据圆锥的体积公式:体积=底面积×高×,高=体积÷底面积÷,代入数据,即可解答。
【详解】3.14×62×[6×(1+)]
=3.14×36×[6×]
=113.04×8
=904.32(立方厘米)
6×=4(厘米)
904.32÷(3.14×42)÷
=904.32÷(3.14×16)÷
=904.32÷50.24÷
=18×3
=54(厘米)
答:熔铸成的圆锥形铁块的高是54厘米。
【点睛】解答本题的关键明确圆柱形铁块熔铸圆锥形铁块,体积不变。
19.(1)36平方厘米
(2)6.4厘米
【分析】(1)根据长方体的体积公式V=abh计算出橡皮泥的体积,再用橡皮泥的体积除以再除以8即可;
(2)用橡皮泥的体积除以圆柱的底面积,就是圆柱的高。
【详解】(1)
4×3×8÷÷8
=288÷8
=36(平方厘米)
答:这个圆锥的底面积是36厘米。
(2)
4×3×8÷15
=96÷15
=6.4(厘米)
答:这个圆柱的高是6.4厘米。
【点睛】此题主要考查等体变形,以及长方体和圆柱、圆锥的体积计算公式。
20.(1)157平方厘米
(2)1177.5毫升
【分析】(1)求装饰带的面积就是求底面直径是10厘米,高是5厘米的圆柱的侧面积,根据圆柱的侧面积公式:面积=底面周长×高,代入数据,即可解答;
(2)求这个茶杯的容积,就是求这个圆柱形茶杯的容积,根据圆柱的容积公式:容积=底面积×高,代入数据,即可解答。
【详解】(1)3.14×10×5
=31.4×5
=157(平方厘米)
答:这个装饰带的面积是157平方厘米。
(2)3.14×(10÷2)2×15
=3.14×25×15
=78.5×15
=1177.5(立方厘米)
1177.5立方厘米=1177.5毫升
答:这个茶杯的容积大约是1177.5毫升。
【点睛】利用圆柱的侧面积公式,圆柱的体积(容积)公式进行解答,关键是熟记公式。
21.1004.8mL
【分析】瓶子的容积可以看作底面直径是8cm,高12cm的圆柱和底面直径是8cm,高8cm的圆柱组成的,因为水的体积不变,上面无水部分的容积也不变,倒置后无水部分的容积可以看作是底面直径是8cm,高8cm的圆柱,由数量关系式:水的体积+无水部分的容积=瓶子的容积,利用圆柱体积公式V=r2h,将相关数据代入,再运用乘法分配律简算即可求得瓶子的容积。
【详解】
=
=
=50.24×20
=1004.8(cm3)
1004.8cm3=1004.8mL
答:这个瓶子的容积是1004.8mL。
【点睛】这是一道关于圆柱的体积计算的题目,理解前后两次瓶子的放置(后面空余部分就是前面的空余部分)是解题的关键。
22.175.8立方分米
【分析】该模型池所占空间,可以用长方体的体积减去半圆柱的体积,根据长方体的体积公式:V=abh,圆柱的体积公式:V=πh,代入数据解答即可。
【详解】
=270-3.14×4×15÷2
=270-94.2
=175.8(立方分米)
答:该模型的体积是175.8立方分米。
【点睛】此题主要是考查圆柱体积、长方体体积的计算,关键是记住相应的计算公式,并能灵活运用。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
圆柱与圆锥专题突破-数学六年级下册北师大版
1.给大厅中一根圆柱形立柱刷漆。已知立柱高4米,底面半径是0.5米,每平方米需油漆0.4千克。将这根立柱全部刷完共需多少千克油漆?
2.一个圆柱茶叶筒的侧面积是188.4平方厘米,底面直径是6厘米。它的高是多少厘米?
3.一个圆柱的侧面展开图恰好是一个边长为18.84厘米的正方形,求这个圆柱体的表面积。
4.把一个底面半径是3分米,长是9分米的圆柱形木头锯成长短不同的五小段圆柱形木头,表面积增加了多少平方分米?
5.芳芳正在制作圆柱,她用下面这张长方形纸做圆柱的侧面,再用其他的纸做上下底面,就可以粘成一个圆柱制作的过程中她发现可以做出两个不同的圆柱,她认为围成的两个不同的圆柱的表面积是相同的,你同意吗?把你的思考过程写一写。取
6.一个圆柱形水池,底面周长是31.4米,深是3米,在池底及池壁抹一层水泥,抹水泥的面积是多少平方米?
7.妙想家经常用一种空心圆柱形状的卷纸(如图),测得这种卷纸的底面外直径是12厘米,内直径是6厘米,高是10厘米。若要给这种卷纸的内、外侧和上、下底面包上一层塑料膜,至少需要多少平方厘米的塑料膜?
8.把一个底面半径为5分米、高为9.6分米的圆锥形零件,改铸成底面直径为8分米的圆柱形零件,铸成的圆柱形零件的高是多少分米?
9.一个圆锥形零件,它的底面半径是5cm.高是底面半径的3倍,这个零件的体积是多少立方厘米?
10.一个圆柱体侧面展开后是一个长6.28厘米,宽3.14厘米的长方形,底面直径是多少厘米?如果把它削成一个最大的圆锥,削去部分的体积是多少?
11.一个底面半径是8cm的圆柱形玻璃器皿装满了水,水中浸着一个底面半径是4cm的圆锥形铅锤,当铅锤从水中取出后,水面下降了2cm.这个铅锤的体积是多少?
12.一个圆柱和一个圆锥等底等高,它们的体积和是50.24立方分米,如果圆锥的底面半径是2分米,这个圆锥的高是多少分米?
13.一个直角三角形的三条边分别为3厘米、4厘米、5厘米,沿它的一条直角边为轴旋转一周,可得什么图形?体积最小是多少?体积最大是多少?
14.有一个圆锥形谷堆(如图),如果把这些谷子放到一个圆柱形粮囤里,可以堆2米高。这个圆柱形粮囤的占地面积是多少?取值
15.小明的妈妈冲了1000毫升的果汁。如果用下图中的玻璃杯喝果汁,小明、爸爸和妈妈每人一杯够吗?
16.在一个底面直径是24厘米的圆柱形容器中,放入一个底面半径是圆柱底面半径的的圆锥形铅锤后,再注满水。当铅锤从水中取出后,水面下降了0.5厘米,铅锤的高是多少厘米?
17.一根圆柱形木料的高是25分米,底面直径比高少,这根木料的表面积是多少平方分米?
18.把一个底面半径是6厘米,高比底面半径多的圆柱形铁块熔铸成一个底面半径是圆柱底面半径的的圆锥形铁块,熔铸成的圆锥形铁块的高是多少厘米?
19.一个长方体橡皮泥如下图:
(1)如果把它捏成同样高的圆锥,这个圆锥的底面积是多少?
(2)如果把这个长方体橡皮泥捏成底面积是15平方厘米的圆柱,这个圆柱的高是多少厘米?
20.爸爸的茶杯(如图)。
(1)小红怕烫伤爸爸的手,特意在茶杯上贴了一个装饰带,这个装饰带的面积是多少?
(2)这个茶杯的容积大约是多少毫升?(玻璃的厚度忽略不计)
21.一个直径是8cm的瓶子里,水的高度是12cm,把瓶盖拧紧倒置放平,无水部分是圆柱形,高度是8cm,这个瓶子的容积是多少?(厚度忽略不计)
22.冬奥会项目设有单板滑香U形池赛,张叔叔根据单板滑雪U形池制作了一个U形池的简化模型(如图),形状可以看为一个长方体中挖去了半个圆柱体(沿高平分)。已知该模型的长为15分米,宽为6分米,高为3分米,其中挖圆柱体的底面直径为4分米。该模型的体积是多少立方分米?
参考答案:
1.5.024千克
【分析】根据题意可知,给圆柱形立柱刷漆,只是刷侧面,底面与顶面不用刷,故根据圆柱侧面积公式:,求出侧面积再乘0.4即可解答。
【详解】2×3.14×0.5×4×0.4
=3.14×4×0.4
=5.024(千克)
答:将这根立柱全部刷完共需5.024千克油漆。
【点睛】此题主要考查学生对圆柱侧面积的理解与求取方法,需要理解给圆柱形立柱刷漆,只是刷侧面,底面与顶面不用刷。
2.10cm
【分析】根据圆柱的侧面积公式:S=πdh,得出h=S÷(πd),代入数据计算即可
【详解】188.4÷(3.14×6)
=188.4÷18.84
=10(cm)
答:它的高是10厘米。
【点睛】本题考查圆柱侧面积公式的逆运用,牢记圆柱的侧面积公式是解题的关键。
3.411.4656平方厘米
【详解】18.84÷3.14÷2=3(厘米)
3.14×32×2+18.84×18.84=411.4656(平方厘米)
4.226.08平方分米
【分析】锯圆柱形木头,表面积增加的部分是若干个相同的底面积.锯成五段,要锯4次,每锯一次增加两个面,锯了4次增加了八个面.
【详解】3.14 × 3 × 8 = 226.08(平方分米)
5.见详解
【分析】由圆柱的侧面展开图的特点可知:圆柱的侧面展开后,是一个长方形,可以先把长方形的长当作底面周长,宽就是圆柱的高,也可以把长方形的宽当作圆柱的底面周长,长就是圆柱的高,求出底面半径,再比较选择即可。
【详解】不同意;因为圆柱的表面积=侧面积个底面积,两个不同的圆柱,侧面积都相等,都等于这个长方形的面积,所以,只要比较底面积即可,底面半径越大,底面积就越大,所以比较半径即可。
18.84÷3.14÷2
=6÷2
=3(cm)
12.56÷3.14÷2
=4÷2
=2(cm)
所以,底面积不同,由此围成的两个不同的圆柱的表面积也是不相同的。
【点睛】解答此题的关键是明白:圆柱的侧面展开后,是一个长方形,反过来,可以把长方形的长当作底面周长,宽等于圆柱的高,也可以把宽当作底面周长,长当作圆柱的高。
6.172.7平方米
【分析】抹水泥的面积为圆柱的侧面积与一个底面积的和,根据侧面积=底面周长×高,底面积=半径×半径×圆周率,将相关数据代入即可解答。
【详解】水池的侧面积:31.4×3=94.2(平方米)
水池的底面积:
3.14×(31.4÷3.14÷2)2
=3.14×52
=3.14×25
=78.5(平方米)
抹水泥部分的面积是:94.2+78.5=172.7(平方米)
答:抹水泥部分的面积是172.7平方米。
【点睛】此题主要考查圆柱表面积公式在实际生活中的应用,关键是熟记公式。
7.734.76平方厘米
【分析】观察题意可知,塑料膜的面积=内侧面积+外侧面积+上、下底的圆环面积,根据圆柱的侧面积公式:S=πdh,用3.14×12×10+3.14×6×10即可求出内外侧的面积和,再根据圆环面积公式:S=π(R2-r2),用3.14×[(12÷2)2-(6÷2)2]×2即可求出上下底的面积,最后把内外侧的面积和加上上下底的面积,即可求出塑料膜的面积。
【详解】3.14×12×10+3.14×6×10
=376.8+188.4
=565.2(平方厘米)
3.14×[(12÷2)2-(6÷2)2] ×2
=3.14×[62-32] ×2
=3.14×[36-9] ×2
=3.14×27×2
=169.56(平方厘米)
565.2+169.56=734.76(平方厘米)
答:至少需要734.76平方厘米的塑料膜。
【点睛】本题主要考查了圆柱侧面积公式以及底面积公式的灵活应用,要注意表面由哪些面组成。
8.5分米
【详解】试题分析:根据题意可知,圆锥钢材的体积等于铸造成的圆柱零件的体积,可先根据圆锥的体积公式求出这个零件的体积,再利用圆柱的高=体积×3÷底面积即可解答.
解:(3.14×52×9.6×)÷[3.14×(8÷2)2]
=251.2÷50.24,
=5(分米),
答:铸成的圆柱形零件的高是5分米.
点评:解答此题的关键是确定圆锥形钢材的体积等于铸造成的圆柱形零件的体积,然后再根据圆锥的体积公式和圆柱的体积公式进行计算即可.
9.392.5立方厘米
【详解】试题分析:根据“底面半径是5dm,高是底面半径的3倍可求出高,再根据圆锥的体积公式,V=Sh,列式解答即可.
解:×3.14×52×(5×3)
=×3.14×25×15,
=392.5(立方厘米);
答:这个零件的体积是392.5立方厘米.
点评:本题主要考查圆锥的体积计算,要牢记圆锥的体积公式V=Sh,不能忘记乘.
10.6.57立方厘米
【详解】试题分析:由圆柱的侧面展开图的特点可知:圆柱的侧面展开得到的是一个长方形,长方形的长等于圆柱底面周长,宽等于圆柱的高;由此根据圆的周长公式,求出这个圆柱体的底面直径.根据圆柱的体积公式:v=sh,把数据代入公式解答;如果把它削成一个最大的圆锥,这个圆锥与圆柱等底等高,因为等底等高的圆锥的体积是圆柱体积的,所以削去部分的体积是圆柱体积的(1),然后根据一个数乘分数的意义解答.
解:底面直径是:6.28÷3.14=2(厘米);
3.14×()2×3.14×(1),
=3.14×1×3.14×,
=9.8596×,
=,
≈6.57(立方厘米);
答:圆柱的底面直径是2厘米,削去部分的体积约是6.57立方厘米.
点评:此题考查的目的是掌握圆柱的侧面展开的特点,以及圆柱体积的计算.
11.401.92立方厘米
【详解】试题分析:圆锥形铅锤的体积就是铅锤从水中取出后,水面下降了2cm,下降的水的体积就是铅锤的体积.下降的这部分水的形状是一个底面半径是8cm的圆柱形,因此求出这个圆柱的体积即可.
解:3.14×82×2,
=3.14×128,
=401.92(立方厘米);
答:这个铅锤的体积是401.92立方厘米
点评:本题考查了圆柱的体积公式的运用,同时考查了学生的转化思想,下降水的体积就是铅锤体积.
12.3分米
【详解】试题分析:根据等底等高的圆柱的体积是圆锥的体积的3倍,把圆锥的体积看作1份,圆柱的体积是3份,它们的和是(1+3)份,由此再根据“它们的体积之和是50.24立方分米”,求出圆锥的体积,再利用圆锥的体积公式求出它的高即可.
解:50.24÷4=12.56(立方分米),
3.14×22=12.56(平方分米),
12.56×3÷12.56=3(分米),
答:圆锥的高是3分米.
点评:此题主要考查了等底等高的圆柱的体积与圆锥的体积的关系,解答时注意找准50.24立方分米的对应倍数.
13.绕着它的任意一条直角边旋转一周可以得到一个圆锥体,这个图形的体积最小是37.68立方厘米,最大是50.24立方厘米
【详解】试题分析:直角三角形绕一条直角边旋转一周,得到的图形是一个圆锥体,由此可知:(1)以4厘米直角边为轴旋转,得到的是底面半径为3厘米,高为4厘米的圆锥;(2)以3厘米的直角边为轴旋转,得到的是一个底面半径为4厘米,高为3厘米的圆锥,由此利用圆锥的体积公式求出它们的体积即可解答.
解::(1)以4厘米直角边为轴旋转,得到的是底面半径为3厘米,高为4厘米的圆锥;
体积为:×3.14×32×4,
=×3.14×9×4,
=37.68(立方厘米);
(2)以3厘米的直角边为轴旋转,得到的是一个底面半径为4厘米,高为3厘米的圆锥,
体积是:×3.14×42×3,
=3.14×16,
=50.24(立方厘米),
答:绕着它的任意一条直角边旋转一周可以得到一个圆锥体,这个图形的体积最小是37.68立方厘米,最大是50.24立方厘米.
点评:此题考查圆锥的体积公式的计算应用,抓住圆锥的展开图的特点,得出直角三角形绕直角边旋转一周得出的是圆锥体是解决本题的关键.
14.3.14平方米
【分析】根据圆锥的体积公式:体积=底面积×高×,代入数据,求出圆锥的体积;圆锥的体积等于高是2米的圆柱的体积,根据圆柱的体积公式:体积=底面积×高;底面积=体积÷高,代入数据,即可解答。
【详解】3.14×22×1.5×÷2
=3.14×4×1.5×÷2
=12.56×1.5×÷2
=18.84×÷2
=6.28÷2
=3.14(平方米)
答:这个圆柱形粮囤的占地面积是3.14平方米。
【点睛】熟练掌握和灵活运用圆柱的体积公式和圆锥的体积公式是解答本题的关键。
15.够
【分析】根据圆柱的体积公式:体积=底面积×高,代入数据,求出玻璃杯的体积,再求出3倍果汁的体积,再和1000毫升比较,如果3倍果汁的体积大于1000毫升,就不够每人一杯;如果3杯果汁的体积小于1000毫升,就够每人一杯,据此解答。
【详解】3.14×(6÷2)2×10
=3.14×9×10
=28.26×10
=282.6(立方厘米)
282.6立方厘米=282.6毫升
282.6×3=847.8(毫升)
847.8<1000,小明、爸爸和妈妈每人一杯够。
答:小明、爸爸和妈妈每人一杯够。
【点睛】熟练掌握圆柱的体积公式以及单位名数的换算是解答本题的关键。
16.3.375厘米
【分析】当铅锤从水中取出后,水面下降的体积就是这个铅锤的体积;根据直径与半径的关系可求出这个圆柱形容器的底面半径,根据圆柱的体积计算公式即可求出水面下降的体积,即铅锤的体积;根据直径与半径的关系可求出圆锥形铅锤,再根据圆锥的体积计算公式“V=r2h”即可求出铅锤高。
【详解】24×=8(厘米)
3.14×()2×0.5×3÷(3.14×82)
=3.14×122×0.5×3÷(3.14×64)
=3.14×144×0.5×3÷(3.14×64)
=678.24÷200.96
=3.375(厘米)
答:铅锤高3.375厘米。
【点睛】此题是考查圆柱、圆锥体积的计算,关键是圆锥体积公式的灵活运用。
17.339.12平方分米
【分析】把故看作单位“1”,根据求一个数的几分之几是多少,用乘法求出底面直径,再根据圆柱的表面积=侧面积+底面积×2,圆柱的侧面积=底面周长×高,圆的面积公式:S=πr2,把数据代入公式解答。
【详解】25×(1-)
=25×
=4(分米)
3.14×4×25+3.14×(4÷2)2×2
=12.56×25+3.14×4×2
=314+25.12
=339.12(平方分米)
答:这个圆柱的表面积是339.12平方分米。
【点睛】此题主要考查圆柱表面积公式的灵活运用,关键是熟记公式。
18.54厘米
【分析】把底面半径看作单位“1”,高是半径的(1+),用半径×(1+),求出圆柱的底面半径;再根据圆柱的体积公式:体积=底面积×高,代入数据,求出圆柱的体积;圆柱铸成圆锥,圆柱的体积等于圆锥的体积;把圆柱的半径看作单位“1”,用圆柱的半径×,代入数据,求出圆锥的半径,再根据圆锥的体积公式:体积=底面积×高×,高=体积÷底面积÷,代入数据,即可解答。
【详解】3.14×62×[6×(1+)]
=3.14×36×[6×]
=113.04×8
=904.32(立方厘米)
6×=4(厘米)
904.32÷(3.14×42)÷
=904.32÷(3.14×16)÷
=904.32÷50.24÷
=18×3
=54(厘米)
答:熔铸成的圆锥形铁块的高是54厘米。
【点睛】解答本题的关键明确圆柱形铁块熔铸圆锥形铁块,体积不变。
19.(1)36平方厘米
(2)6.4厘米
【分析】(1)根据长方体的体积公式V=abh计算出橡皮泥的体积,再用橡皮泥的体积除以再除以8即可;
(2)用橡皮泥的体积除以圆柱的底面积,就是圆柱的高。
【详解】(1)
4×3×8÷÷8
=288÷8
=36(平方厘米)
答:这个圆锥的底面积是36厘米。
(2)
4×3×8÷15
=96÷15
=6.4(厘米)
答:这个圆柱的高是6.4厘米。
【点睛】此题主要考查等体变形,以及长方体和圆柱、圆锥的体积计算公式。
20.(1)157平方厘米
(2)1177.5毫升
【分析】(1)求装饰带的面积就是求底面直径是10厘米,高是5厘米的圆柱的侧面积,根据圆柱的侧面积公式:面积=底面周长×高,代入数据,即可解答;
(2)求这个茶杯的容积,就是求这个圆柱形茶杯的容积,根据圆柱的容积公式:容积=底面积×高,代入数据,即可解答。
【详解】(1)3.14×10×5
=31.4×5
=157(平方厘米)
答:这个装饰带的面积是157平方厘米。
(2)3.14×(10÷2)2×15
=3.14×25×15
=78.5×15
=1177.5(立方厘米)
1177.5立方厘米=1177.5毫升
答:这个茶杯的容积大约是1177.5毫升。
【点睛】利用圆柱的侧面积公式,圆柱的体积(容积)公式进行解答,关键是熟记公式。
21.1004.8mL
【分析】瓶子的容积可以看作底面直径是8cm,高12cm的圆柱和底面直径是8cm,高8cm的圆柱组成的,因为水的体积不变,上面无水部分的容积也不变,倒置后无水部分的容积可以看作是底面直径是8cm,高8cm的圆柱,由数量关系式:水的体积+无水部分的容积=瓶子的容积,利用圆柱体积公式V=r2h,将相关数据代入,再运用乘法分配律简算即可求得瓶子的容积。
【详解】
=
=
=50.24×20
=1004.8(cm3)
1004.8cm3=1004.8mL
答:这个瓶子的容积是1004.8mL。
【点睛】这是一道关于圆柱的体积计算的题目,理解前后两次瓶子的放置(后面空余部分就是前面的空余部分)是解题的关键。
22.175.8立方分米
【分析】该模型池所占空间,可以用长方体的体积减去半圆柱的体积,根据长方体的体积公式:V=abh,圆柱的体积公式:V=πh,代入数据解答即可。
【详解】
=270-3.14×4×15÷2
=270-94.2
=175.8(立方分米)
答:该模型的体积是175.8立方分米。
【点睛】此题主要是考查圆柱体积、长方体体积的计算,关键是记住相应的计算公式,并能灵活运用。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
