数学人教A版(2019)必修第一册2.3二次函数与一元二次方程、不等式 课件(共27张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册2.3二次函数与一元二次方程、不等式 课件(共27张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-22 07:10:10 | ||
图片预览







文档简介
(共27张PPT)
人教版必修一(A版)
2.3 《二次函数与一元二次方程、不等式 》
(2课时 )
教学目标
学习目标:1、了解一元二次不等式的概念;2、认识与理解一元二次不等式与一元二次方程、二次函数之间的关系;3、深刻掌握一元二次不等式的图像解法.
教学重点:一元二次不等式的图像解法.
教学难点:一元二次不等式与一元二次方程、二次函数之间的关系.
一
复习旧知——一元二次方程与二次函数(导学)
1、问题:
各位同学,在初中我们已经学习了一元二次方程与二次函数的相关知识,那么大家还能对这些知识进行阐述并灵活运用吗?
一
复习旧知——一元二次方程与二次函数(导学)
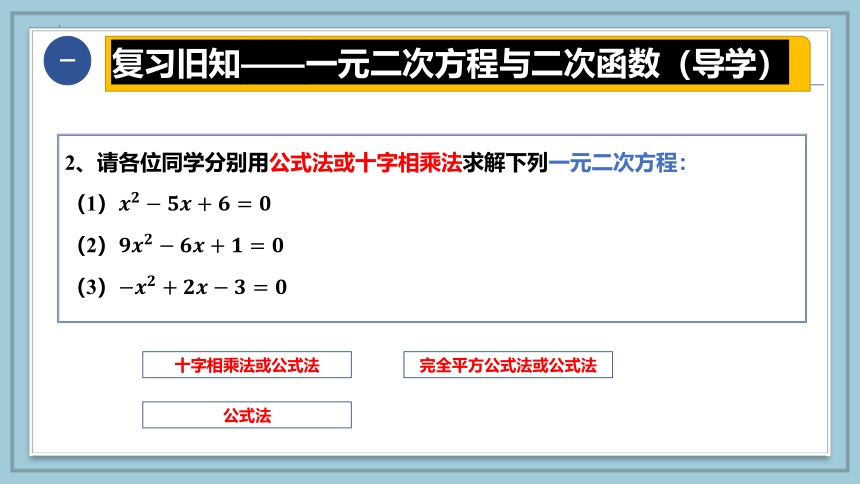
2、请各位同学分别用公式法或十字相乘法求解下列一元二次方程:
(1)
(2)
(3)
十字相乘法或公式法
完全平方公式法或公式法
公式法
一
复习旧知——一元二次方程与二次函数(导学)
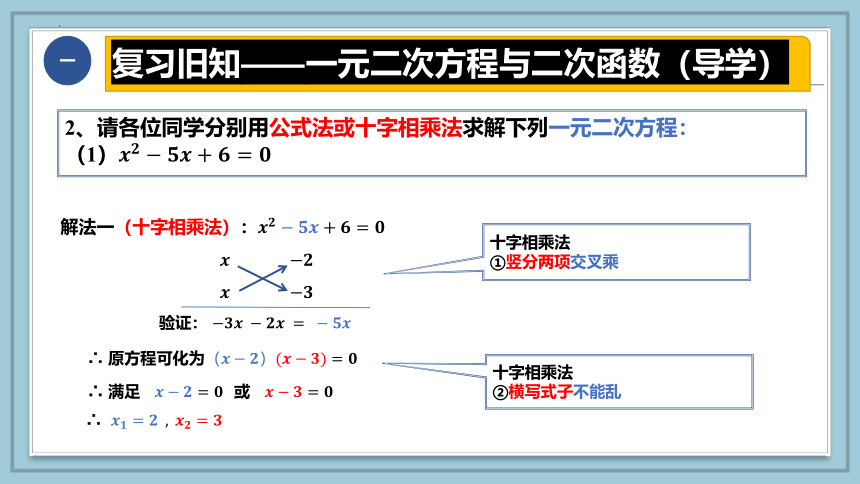
2、请各位同学分别用公式法或十字相乘法求解下列一元二次方程:
(1)
解法一(十字相乘法):
验证:
∴ 原方程可化为
∴ 满足 或
∴
十字相乘法
①竖分两项交叉乘
十字相乘法
②横写式子不能乱
一
复习旧知——一元二次方程与二次函数(导学)
2、请各位同学分别用公式法或十字相乘法求解下列一元二次方程:
(1)
解法二(公式法):
∵ 已知
∴
又∵
∴ 原一元二次方程有两个不相等的实数根,分别为
∴
用公式法求解一元二次方程
①判别式
②求根公式
A.当 时,原一元二次方程有两个不相等的实数根
B.当 时,原一元二次方程有两个相等的实数根(或只有一个实数根)
C.当 时,原一元二次方程没有实数根
一
复习旧知——一元二次方程与二次函数(导学)
解法一(公式法):
∵ 已知
∴
又∵
∴ 原一元二次方程有两个相等的实数根,分别为
∴
2、请各位同学分别用公式法或十字相乘法求解下列一元二次方程:
(2)
解法二(完全平方公式法):
∵ 已知
∴
∴
∴
∴
即原一元二次方程的实数根为
一
复习旧知——一元二次方程与二次函数(导学)
解(公式法):
∵ 已知
即
∴
又∵
∴ 原一元二次方程没有实数根
2、请各位同学分别用公式法或十字相乘法求解下列一元二次方程:
(3)
一
复习旧知——一元二次方程与二次函数(导学)
3、问题:请各位同学将二次函数 转化为它的顶点式与交点式,并画出它的图像?
解:∵ 已知
∴ +15
+ 15
+ 15
+ 15
∴
∴抛物线的开口向下,且顶点坐标为( )
二次函数的配方
①化二次项系数为1:用含未知数的项除以二次项即可得到括号里面的项,常数项照搬
②配方:利用对消思想,括号内同时加上和减去一次项系数绝对值一半的平方,从而构造出完全平方公式
③整理:去括号,合并同类项,将二次函数解析式化为顶点式 ,则可判断出抛物线的开口方向与顶点坐标
一
复习旧知——一元二次方程与二次函数(导学)
3、问题:请各位同学将二次函数 转化为它的顶点式与交点式,并画出它的图像?
又令, 利用整体思想则有 于是可得这个二次函数的交点式为
其图像如下所示:
验证:
∴满足
解得
∴ 抛物线 与轴的两个交点坐标分别为
一
复习旧知——一元二次方程与二次函数(导学)
4、小结:二次函数与一元二次方程的关系
令,利用整体思想则可将二次函数转化为一元二次方程
(1)从几何的角度:对于抛物线上的点,当点的纵坐标时,这样的点即为抛物线与轴的交点
(2)从代数的角度:对于一元二次方程,解这个一元二次方程得到的实数根就是它所对应的二次函数图像与轴的交点的横坐标
一
复习旧知——一元二次方程与二次函数(导学)
4、小结:二次函数与一元二次方程的关系
二
情景问题
为喜迎2022年10月16日-22日,即将在北京召开的党的二十大,营造喜庆、隆重、热烈的氛围,某市园林规划局计划在市中心公园一块长为8米,宽为6 米的长方形地面上进行“喜迎二十大、花开向未来”主题绿化设计活动.
计划四周种草坪,草坪带的宽度相同,中间种植花卉.为了凸显喜庆隆重的氛围,要求花卉的种植面积要超过总面积的一半,此时草坪带宽度的取值范围是多少
情景问题
各位同学,绿化设计简要图纸如下所示,你们能根据设计要求列出不等式,并求出草坪带宽度的取值范围是多少吗
二
情景问题
问 题
你们知道这个不等式如何求解吗?相信各位同学通过今天的学习,将能解决这一问题.
二
三
探究新知1——一元二次不等式的概念
注:上面一般式中的“>”也可以换成“<”,“≥”或“≤”.
像这样,含有 ,并且 的不等式,就称为一元二次不等式.
一个未知数
含有未知数项的最高次数为2
四
探究新知2——一元二次不等式的解法
思考:抢答
( -∞,-1 ) ∪(3,+∞)
1、不等式 的解集为 .
2、不等式 的解集为 .
[ -1 ,3 ]
3、不等式 的解集为 .
(-∞,-1]∪[3,+∞)
探究新知2——一元二次不等式的解法
一元二次不等式的求解方法小结
一 化
二 解
三作图
四 答
通常要将不等式的解集用数集或区间来表示.
四
五
各位同学,请大家每4个人组成一组,分别交流讨论后,求解下列一元二次不等式的解集:
小组合作、讨论交流
(1)
(2)
(3)
六
成果展示
例1 求不等式的解集.
解:∵ 已知
∴
又∵
∴解一元二次方程可得:
又∵二次项系数 ,
∴可得二次函数的图像
如下图所示:
由图可知原一元二次不等式的解集为
成果展示
例2 求不等式的解集.
解:∵ 已知
∴
又∵
∴解一元二次方程可得
又∵二次项系数 ,
∴可得二次函数的图像
如下图所示:
由图可知原一元二次不等式的解集为
+
六
成果展示
例3 求不等式的解集.
解:原不等式 可化为
∴
又∵
∴ 一元二次方程没有实数根
又∵二次项系数 ,
∴可得二次函数的图像
如下图所示:
由图可知一元二次不等式
的解集为
故原一元二次不等式的解集为
六
提升演练(检测实践)
例3 求不等式的解集.
解:原不等式 可化为
∴
又∵
∴ 一元二次方程没有实数根
又∵二次项系数 ,
∴可得二次函数的图像
如下图所示:
由图可知一元二次不等式
的解集为
故原一元二次不等式的解集为
七
∵
∴
∴解一元二次方程可得:
又∵二次项系数 ,
∴可得二次函数的图像
如下图所示:
由图可知原一元二次不等式的解集为
又∵
∴要使花卉的种植面积超过总面积的一半,此时草坪带宽度 的取值范围是
家庭作业
1、完成《学习指导与练习》第15、16页题型;
2、记背今天所学习一元二次不等式的相关知识与课堂训练作业.
八
九
学生自评
请学科代表对今天这堂课的优秀小组以及优秀学员进行点评!
十
课程结束
感谢各位老师的莅临指导聆听、以及各位同学的积极配合!
人教版必修一(A版)
2.3 《二次函数与一元二次方程、不等式 》
(2课时 )
教学目标
学习目标:1、了解一元二次不等式的概念;2、认识与理解一元二次不等式与一元二次方程、二次函数之间的关系;3、深刻掌握一元二次不等式的图像解法.
教学重点:一元二次不等式的图像解法.
教学难点:一元二次不等式与一元二次方程、二次函数之间的关系.
一
复习旧知——一元二次方程与二次函数(导学)
1、问题:
各位同学,在初中我们已经学习了一元二次方程与二次函数的相关知识,那么大家还能对这些知识进行阐述并灵活运用吗?
一
复习旧知——一元二次方程与二次函数(导学)
2、请各位同学分别用公式法或十字相乘法求解下列一元二次方程:
(1)
(2)
(3)
十字相乘法或公式法
完全平方公式法或公式法
公式法
一
复习旧知——一元二次方程与二次函数(导学)
2、请各位同学分别用公式法或十字相乘法求解下列一元二次方程:
(1)
解法一(十字相乘法):
验证:
∴ 原方程可化为
∴ 满足 或
∴
十字相乘法
①竖分两项交叉乘
十字相乘法
②横写式子不能乱
一
复习旧知——一元二次方程与二次函数(导学)
2、请各位同学分别用公式法或十字相乘法求解下列一元二次方程:
(1)
解法二(公式法):
∵ 已知
∴
又∵
∴ 原一元二次方程有两个不相等的实数根,分别为
∴
用公式法求解一元二次方程
①判别式
②求根公式
A.当 时,原一元二次方程有两个不相等的实数根
B.当 时,原一元二次方程有两个相等的实数根(或只有一个实数根)
C.当 时,原一元二次方程没有实数根
一
复习旧知——一元二次方程与二次函数(导学)
解法一(公式法):
∵ 已知
∴
又∵
∴ 原一元二次方程有两个相等的实数根,分别为
∴
2、请各位同学分别用公式法或十字相乘法求解下列一元二次方程:
(2)
解法二(完全平方公式法):
∵ 已知
∴
∴
∴
∴
即原一元二次方程的实数根为
一
复习旧知——一元二次方程与二次函数(导学)
解(公式法):
∵ 已知
即
∴
又∵
∴ 原一元二次方程没有实数根
2、请各位同学分别用公式法或十字相乘法求解下列一元二次方程:
(3)
一
复习旧知——一元二次方程与二次函数(导学)
3、问题:请各位同学将二次函数 转化为它的顶点式与交点式,并画出它的图像?
解:∵ 已知
∴ +15
+ 15
+ 15
+ 15
∴
∴抛物线的开口向下,且顶点坐标为( )
二次函数的配方
①化二次项系数为1:用含未知数的项除以二次项即可得到括号里面的项,常数项照搬
②配方:利用对消思想,括号内同时加上和减去一次项系数绝对值一半的平方,从而构造出完全平方公式
③整理:去括号,合并同类项,将二次函数解析式化为顶点式 ,则可判断出抛物线的开口方向与顶点坐标
一
复习旧知——一元二次方程与二次函数(导学)
3、问题:请各位同学将二次函数 转化为它的顶点式与交点式,并画出它的图像?
又令, 利用整体思想则有 于是可得这个二次函数的交点式为
其图像如下所示:
验证:
∴满足
解得
∴ 抛物线 与轴的两个交点坐标分别为
一
复习旧知——一元二次方程与二次函数(导学)
4、小结:二次函数与一元二次方程的关系
令,利用整体思想则可将二次函数转化为一元二次方程
(1)从几何的角度:对于抛物线上的点,当点的纵坐标时,这样的点即为抛物线与轴的交点
(2)从代数的角度:对于一元二次方程,解这个一元二次方程得到的实数根就是它所对应的二次函数图像与轴的交点的横坐标
一
复习旧知——一元二次方程与二次函数(导学)
4、小结:二次函数与一元二次方程的关系
二
情景问题
为喜迎2022年10月16日-22日,即将在北京召开的党的二十大,营造喜庆、隆重、热烈的氛围,某市园林规划局计划在市中心公园一块长为8米,宽为6 米的长方形地面上进行“喜迎二十大、花开向未来”主题绿化设计活动.
计划四周种草坪,草坪带的宽度相同,中间种植花卉.为了凸显喜庆隆重的氛围,要求花卉的种植面积要超过总面积的一半,此时草坪带宽度的取值范围是多少
情景问题
各位同学,绿化设计简要图纸如下所示,你们能根据设计要求列出不等式,并求出草坪带宽度的取值范围是多少吗
二
情景问题
问 题
你们知道这个不等式如何求解吗?相信各位同学通过今天的学习,将能解决这一问题.
二
三
探究新知1——一元二次不等式的概念
注:上面一般式中的“>”也可以换成“<”,“≥”或“≤”.
像这样,含有 ,并且 的不等式,就称为一元二次不等式.
一个未知数
含有未知数项的最高次数为2
四
探究新知2——一元二次不等式的解法
思考:抢答
( -∞,-1 ) ∪(3,+∞)
1、不等式 的解集为 .
2、不等式 的解集为 .
[ -1 ,3 ]
3、不等式 的解集为 .
(-∞,-1]∪[3,+∞)
探究新知2——一元二次不等式的解法
一元二次不等式的求解方法小结
一 化
二 解
三作图
四 答
通常要将不等式的解集用数集或区间来表示.
四
五
各位同学,请大家每4个人组成一组,分别交流讨论后,求解下列一元二次不等式的解集:
小组合作、讨论交流
(1)
(2)
(3)
六
成果展示
例1 求不等式的解集.
解:∵ 已知
∴
又∵
∴解一元二次方程可得:
又∵二次项系数 ,
∴可得二次函数的图像
如下图所示:
由图可知原一元二次不等式的解集为
成果展示
例2 求不等式的解集.
解:∵ 已知
∴
又∵
∴解一元二次方程可得
又∵二次项系数 ,
∴可得二次函数的图像
如下图所示:
由图可知原一元二次不等式的解集为
+
六
成果展示
例3 求不等式的解集.
解:原不等式 可化为
∴
又∵
∴ 一元二次方程没有实数根
又∵二次项系数 ,
∴可得二次函数的图像
如下图所示:
由图可知一元二次不等式
的解集为
故原一元二次不等式的解集为
六
提升演练(检测实践)
例3 求不等式的解集.
解:原不等式 可化为
∴
又∵
∴ 一元二次方程没有实数根
又∵二次项系数 ,
∴可得二次函数的图像
如下图所示:
由图可知一元二次不等式
的解集为
故原一元二次不等式的解集为
七
∵
∴
∴解一元二次方程可得:
又∵二次项系数 ,
∴可得二次函数的图像
如下图所示:
由图可知原一元二次不等式的解集为
又∵
∴要使花卉的种植面积超过总面积的一半,此时草坪带宽度 的取值范围是
家庭作业
1、完成《学习指导与练习》第15、16页题型;
2、记背今天所学习一元二次不等式的相关知识与课堂训练作业.
八
九
学生自评
请学科代表对今天这堂课的优秀小组以及优秀学员进行点评!
十
课程结束
感谢各位老师的莅临指导聆听、以及各位同学的积极配合!
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
