1.5弹性碰撞和非弹性碰撞 课件(共23张PPT) 人教版(2019)选择性必修第一册
文档属性
| 名称 | 1.5弹性碰撞和非弹性碰撞 课件(共23张PPT) 人教版(2019)选择性必修第一册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 7.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-03-24 10:29:20 | ||
图片预览





文档简介
(共23张PPT)
5 弹性碰撞和非弹性碰撞
新课引入
陨石撞击地球而对地表产生破坏
网球受球拍撞击而改变运动状态
新课引入
碰碰车之间的碰撞给人们带来快乐
汽车之间的碰撞给人们带来灾难
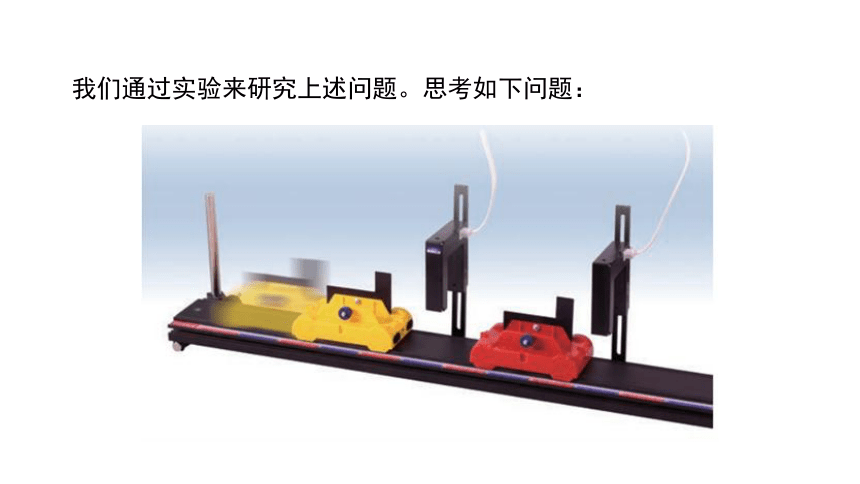
我们通过实验来研究上述问题。思考如下问题:
一、弹性碰撞和非弹性碰撞
仔细观察上图的实验装置,想一想,总动能减少的原因是什么?
一、弹性碰撞和非弹性碰撞
为了尽量减少总动能的损失,可以对上图的实验装置怎样进行改进?
需要测量哪些实验数据?如何测量?
为两辆小车安装弹性碰撞架
碰撞过程中部分机械能转化为了内能,总动能减少。
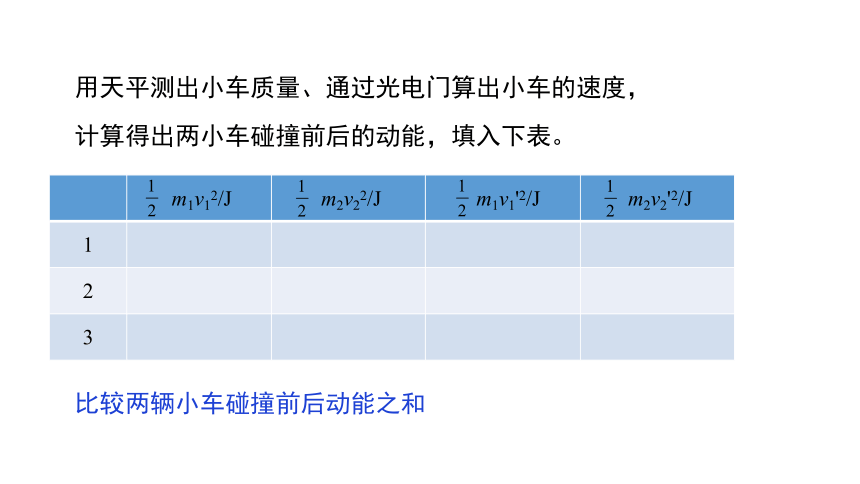
用天平测出小车质量、通过光电门算出小车的速度,
一、弹性碰撞和非弹性碰撞
m1v12/J m2v22/J m1v1'2/J m2v2'2/J
1
2
3
比较两辆小车碰撞前后动能之和
计算得出两小车碰撞前后的动能,填入下表。
一、弹性碰撞和非弹性碰撞
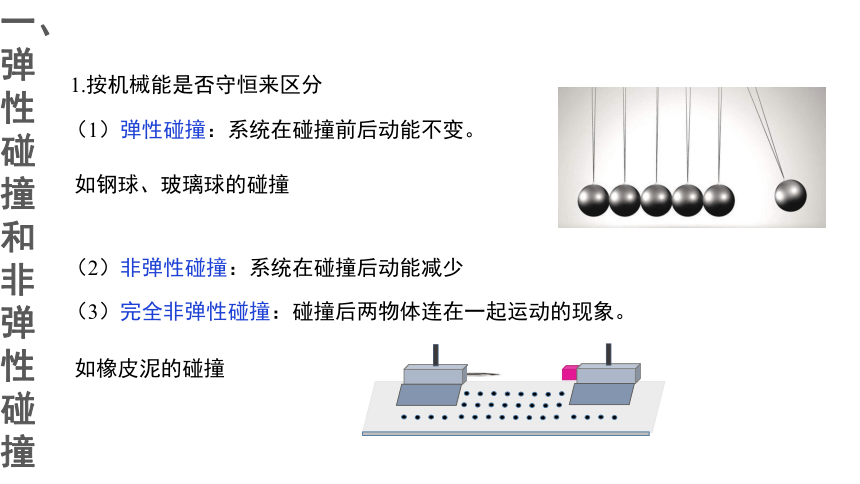
1.按机械能是否守恒来区分
(1)弹性碰撞:系统在碰撞前后动能不变。
如钢球、玻璃球的碰撞
(2)非弹性碰撞:系统在碰撞后动能减少
(3)完全非弹性碰撞:碰撞后两物体连在一起运动的现象。
如橡皮泥的碰撞
一、弹性碰撞和非弹性碰撞
2.从碰撞速度方向来区分
(1)正碰(对心碰撞或一维碰撞):两个小球碰撞前后运动速度与
两球心的连线在同一条直线上
(2)斜碰(非对心碰撞):两个小球碰撞前后运动速度与两球心的
连线不在同一条直线上
v1
v1'
v2
v1
v1'
v2
一、弹性碰撞和非弹性碰撞
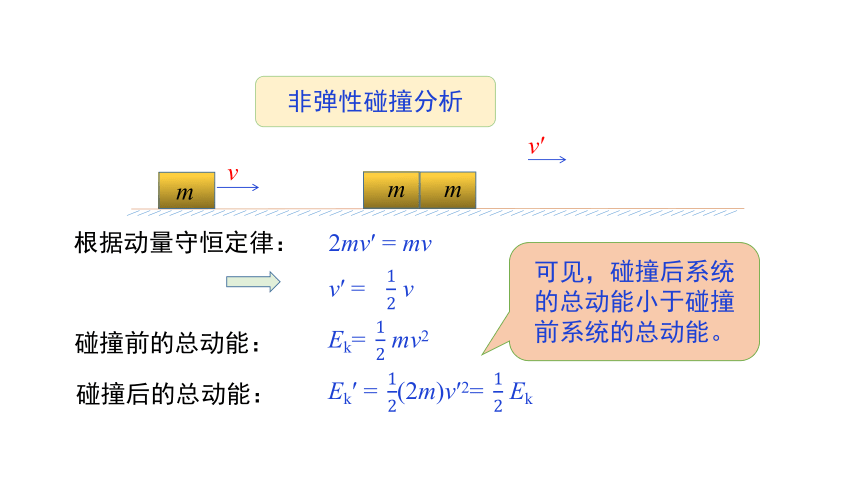
非弹性碰撞分析
m
m
v
m
v′
根据动量守恒定律:
2mv′ = mv
v′ = v
碰撞前的总动能:
Ek= mv2
碰撞后的总动能:
Ek′ =(2m)v′2= Ek
可见,碰撞后系统的总动能小于碰撞前系统的总动能。
运动物体与静止物体碰撞
v1
v1'
v2'
二、弹性碰撞的实例分析
弹性碰撞实例分析
m1
m2
m1
根据动量守恒定律:
m1v1=m1v1′+m2v2′
根据机械能守恒定律:
m1v12=m1v1′2+m2v2′2
两式联立可得:
v1′=v1
v2′=v1
二、弹性碰撞的实例分析
(1)若m1=m2
m1-m2=0
m1+m2=2m1
v1′=0
v2′=v1
质量相等的物体发生弹性碰撞,速度发生交换。
二、弹性碰撞的实例分析
(2)若m1>>m2
m1-m2≈m1
m1+m2≈m1
v1′= v1
v2′= 2v1
第一个物体的速度几乎没有改变,而第二个物体以2v1的速度被撞击出去。
二、弹性碰撞的实例分析
(3)若m1<m1-m2≈-m2
≈0
v1′= -v1
v2′= 0
第一个物体被原速率反弹回去,而第二个物体仍然静止。
v1′= -v1
v1
v2′= 0
典题剖析
例1 (多选)在光滑水平面上,两球沿球心连线以相等速率相向而行,并发生碰撞,下列现象可能的是( )
A.若两球质量相等,碰后以某一相等速率互相分开
B.若两球质量相等,碰后以某一相等速率同向而行
C.若两球质量不等,碰后以某一相等速率互相分开
D.若两球质量不等,碰后以某一相等速率同向而行
AD
例2 如图所示,P物体与一个连着弹簧的Q物体正碰,碰撞后P物体静止,Q物体以P物体碰撞前速度v离开,已知P与Q质量相等,弹簧质量忽略不计,那么当弹簧被压缩至最短时,下列的结论中正确的应是( )
A.P的速度恰好为零
B.P与Q具有相同速度
C.Q刚开始运动
D.Q的速度等于v
解析:P物体接触弹簧后,在弹簧弹力的作用下,P做减速运动,Q物体做加速运动,P、Q间的距离减小,当P、Q两物体速度相等时,弹簧被压缩到最短,所以B正确,A、C错误。由于作用过程中动量守恒,设速度相等时速度为v′,则mv=(m+m)v′,所以弹簧被压缩至最短时,P、Q的速度v′=v,故D错误。
B
典题剖析
例3 (多选)如图甲所示,在光滑水平面上的两小球A、B发生正碰,小球A的质量为m1=0.1 kg。图乙为它们碰撞前后两个小球的s-t图像。由此可以判断( )
A.碰前小球B静止,小球A向右运动
B.碰后小球A和B都向右运动
C.小球B的质量为m2=0.2 kg
D.小球B的质量为m2=0.3 kg
典题剖析
解析:由s-t图象的斜率得到,碰前B的位移不随时间而变化,处于静止,A速度大小为v1==4 m/s,方向只有向右才能与B相撞,故A正确;由s-t图像可知,碰后B的速度为正方向,说明向右运动,A的速度为负方向,说明向左运动,两小球运动方向相反,故B错误;由s-t图像可知,碰后B和A的速度分别为v2′=2 m/s,v1′=-2 m/s,根据动量守恒定律得m1v1=m2v2′+m1v1′,代入解得m2=0.3 kg,故C错误,D正确。故选A、D。
典题剖析
例4 A、B两球在水平光滑直轨道上同向运动,已知它们的动量分别是pA=5 kg·m/s, pB =7 kg·m/s。A从后面追上B并发生碰撞,碰后B的动量pB ′=10 kg·m/s,试分析两球质量的关系。
分析:碰撞问题的三个解题依据
1.动量守恒:
p1+p2=p1′+p2′
2.动能不增加:
Ek1 + Ek2≥Ek1′ + Ek2′
+ +
典题剖析
3.速度要符合情境:
如果碰前两物体同向运动,则后面物体的速度必大于前面物体的速度,即v后>v前,否则无法实现碰撞.
碰撞后,原来在前的物体的速度一定增大,且原来在前的物体速度大于或等于原来在后的物体的速度.即v前′≥v后′ ,否则碰撞没有结束
如果碰前两物体是相向运动,则碰后,两物体的运动方向不可能都不改变,除非两物体碰撞后速度均为零.
典题剖析
解析:由碰撞中动量守恒可求得
要使A追上B,则必有vA>vB,即
碰后pA′、pB′均大于0,表示同向运动,则应有:vB′≥vA′,即
则mB≤5mA。
碰撞过程中,动能不增加,则有
+ ≥ +
解得mB≥mA。
综上可知
mA≤mB≤5mA
典题剖析
例4 A、B两球在水平光滑直轨道上同向运动,已知它们的动量分别是pA=5 kg·m/s, pB =7 kg·m/s。A从后面追上B并发生碰撞,碰后B的动量pB ′=10 kg·m/s,试分析两球质量的关系。
得mB>1.4mA。
pA′=2 kg·m/s
课堂小结
弹性碰撞和非弹性碰撞
弹性碰撞
非弹性碰撞
动量守恒
机械能守恒
动碰静实例分析
动量守恒
机械能不守恒
v1′=v1
v2′=v1
5 弹性碰撞和非弹性碰撞
新课引入
陨石撞击地球而对地表产生破坏
网球受球拍撞击而改变运动状态
新课引入
碰碰车之间的碰撞给人们带来快乐
汽车之间的碰撞给人们带来灾难
我们通过实验来研究上述问题。思考如下问题:
一、弹性碰撞和非弹性碰撞
仔细观察上图的实验装置,想一想,总动能减少的原因是什么?
一、弹性碰撞和非弹性碰撞
为了尽量减少总动能的损失,可以对上图的实验装置怎样进行改进?
需要测量哪些实验数据?如何测量?
为两辆小车安装弹性碰撞架
碰撞过程中部分机械能转化为了内能,总动能减少。
用天平测出小车质量、通过光电门算出小车的速度,
一、弹性碰撞和非弹性碰撞
m1v12/J m2v22/J m1v1'2/J m2v2'2/J
1
2
3
比较两辆小车碰撞前后动能之和
计算得出两小车碰撞前后的动能,填入下表。
一、弹性碰撞和非弹性碰撞
1.按机械能是否守恒来区分
(1)弹性碰撞:系统在碰撞前后动能不变。
如钢球、玻璃球的碰撞
(2)非弹性碰撞:系统在碰撞后动能减少
(3)完全非弹性碰撞:碰撞后两物体连在一起运动的现象。
如橡皮泥的碰撞
一、弹性碰撞和非弹性碰撞
2.从碰撞速度方向来区分
(1)正碰(对心碰撞或一维碰撞):两个小球碰撞前后运动速度与
两球心的连线在同一条直线上
(2)斜碰(非对心碰撞):两个小球碰撞前后运动速度与两球心的
连线不在同一条直线上
v1
v1'
v2
v1
v1'
v2
一、弹性碰撞和非弹性碰撞
非弹性碰撞分析
m
m
v
m
v′
根据动量守恒定律:
2mv′ = mv
v′ = v
碰撞前的总动能:
Ek= mv2
碰撞后的总动能:
Ek′ =(2m)v′2= Ek
可见,碰撞后系统的总动能小于碰撞前系统的总动能。
运动物体与静止物体碰撞
v1
v1'
v2'
二、弹性碰撞的实例分析
弹性碰撞实例分析
m1
m2
m1
根据动量守恒定律:
m1v1=m1v1′+m2v2′
根据机械能守恒定律:
m1v12=m1v1′2+m2v2′2
两式联立可得:
v1′=v1
v2′=v1
二、弹性碰撞的实例分析
(1)若m1=m2
m1-m2=0
m1+m2=2m1
v1′=0
v2′=v1
质量相等的物体发生弹性碰撞,速度发生交换。
二、弹性碰撞的实例分析
(2)若m1>>m2
m1-m2≈m1
m1+m2≈m1
v1′= v1
v2′= 2v1
第一个物体的速度几乎没有改变,而第二个物体以2v1的速度被撞击出去。
二、弹性碰撞的实例分析
(3)若m1<
≈0
v1′= -v1
v2′= 0
第一个物体被原速率反弹回去,而第二个物体仍然静止。
v1′= -v1
v1
v2′= 0
典题剖析
例1 (多选)在光滑水平面上,两球沿球心连线以相等速率相向而行,并发生碰撞,下列现象可能的是( )
A.若两球质量相等,碰后以某一相等速率互相分开
B.若两球质量相等,碰后以某一相等速率同向而行
C.若两球质量不等,碰后以某一相等速率互相分开
D.若两球质量不等,碰后以某一相等速率同向而行
AD
例2 如图所示,P物体与一个连着弹簧的Q物体正碰,碰撞后P物体静止,Q物体以P物体碰撞前速度v离开,已知P与Q质量相等,弹簧质量忽略不计,那么当弹簧被压缩至最短时,下列的结论中正确的应是( )
A.P的速度恰好为零
B.P与Q具有相同速度
C.Q刚开始运动
D.Q的速度等于v
解析:P物体接触弹簧后,在弹簧弹力的作用下,P做减速运动,Q物体做加速运动,P、Q间的距离减小,当P、Q两物体速度相等时,弹簧被压缩到最短,所以B正确,A、C错误。由于作用过程中动量守恒,设速度相等时速度为v′,则mv=(m+m)v′,所以弹簧被压缩至最短时,P、Q的速度v′=v,故D错误。
B
典题剖析
例3 (多选)如图甲所示,在光滑水平面上的两小球A、B发生正碰,小球A的质量为m1=0.1 kg。图乙为它们碰撞前后两个小球的s-t图像。由此可以判断( )
A.碰前小球B静止,小球A向右运动
B.碰后小球A和B都向右运动
C.小球B的质量为m2=0.2 kg
D.小球B的质量为m2=0.3 kg
典题剖析
解析:由s-t图象的斜率得到,碰前B的位移不随时间而变化,处于静止,A速度大小为v1==4 m/s,方向只有向右才能与B相撞,故A正确;由s-t图像可知,碰后B的速度为正方向,说明向右运动,A的速度为负方向,说明向左运动,两小球运动方向相反,故B错误;由s-t图像可知,碰后B和A的速度分别为v2′=2 m/s,v1′=-2 m/s,根据动量守恒定律得m1v1=m2v2′+m1v1′,代入解得m2=0.3 kg,故C错误,D正确。故选A、D。
典题剖析
例4 A、B两球在水平光滑直轨道上同向运动,已知它们的动量分别是pA=5 kg·m/s, pB =7 kg·m/s。A从后面追上B并发生碰撞,碰后B的动量pB ′=10 kg·m/s,试分析两球质量的关系。
分析:碰撞问题的三个解题依据
1.动量守恒:
p1+p2=p1′+p2′
2.动能不增加:
Ek1 + Ek2≥Ek1′ + Ek2′
+ +
典题剖析
3.速度要符合情境:
如果碰前两物体同向运动,则后面物体的速度必大于前面物体的速度,即v后>v前,否则无法实现碰撞.
碰撞后,原来在前的物体的速度一定增大,且原来在前的物体速度大于或等于原来在后的物体的速度.即v前′≥v后′ ,否则碰撞没有结束
如果碰前两物体是相向运动,则碰后,两物体的运动方向不可能都不改变,除非两物体碰撞后速度均为零.
典题剖析
解析:由碰撞中动量守恒可求得
要使A追上B,则必有vA>vB,即
碰后pA′、pB′均大于0,表示同向运动,则应有:vB′≥vA′,即
则mB≤5mA。
碰撞过程中,动能不增加,则有
+ ≥ +
解得mB≥mA。
综上可知
mA≤mB≤5mA
典题剖析
例4 A、B两球在水平光滑直轨道上同向运动,已知它们的动量分别是pA=5 kg·m/s, pB =7 kg·m/s。A从后面追上B并发生碰撞,碰后B的动量pB ′=10 kg·m/s,试分析两球质量的关系。
得mB>1.4mA。
pA′=2 kg·m/s
课堂小结
弹性碰撞和非弹性碰撞
弹性碰撞
非弹性碰撞
动量守恒
机械能守恒
动碰静实例分析
动量守恒
机械能不守恒
v1′=v1
v2′=v1
