2023-2024学年苏科版九年级数学下册第8章《统计和概率的简单应用》检测卷(含解析)
文档属性
| 名称 | 2023-2024学年苏科版九年级数学下册第8章《统计和概率的简单应用》检测卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-22 10:07:48 | ||
图片预览




文档简介
2023-2024学年九年级数学下册检测卷
第8章《统计和概率的简单应用》
考试时间:120分钟,试卷满分:100分
姓名:_________ 班级:_________ 学号:_________
一、选择题(共10小题,满分20分,每小题2分)
1.(2分)(2013春 建湖县校级月考)随机掷一枚均匀的硬币两次,两次正面都朝上的概率是( )
A. B. C. D.1
2.(2分)(2021 张店区二模)“抛掷一枚均匀硬币,落地后正面朝上”这一事件是( )
A.确定事件 B.必然事件 C.随机事件 D.不可能事件
3.(2分)(2023 定远县校级三模)下列四个统计图中,用来表示不同品种的奶牛的日平均产奶量最为合适的是( )
A. B.
C. D.
4.(2分)(2023 镇江二模)下列调查适合抽样调查的是( )
A.企业招聘,对应聘人员进行面试
B.检测航天飞船的设备零件的质量情况
C.检测一批汽车轮胎的使用寿命
D.全国人口普查
5.(2分)(2023 蚌山区一模)在一个不透明的口袋中,放置6个黄球、1个红球和n个蓝球,这些小球除颜色外其余均相同,课外兴趣小组每次摸出一个球记录下颜色后再放回,并且统计了黄球出现的频率,如图,则n的值是( )
A.2 B.3 C.5 D.8
6.(2分)(2023 长沙)长沙市某一周内每日最高气温情况如图所示,下列说法中,错误的是( )
A.这周最高气温是32℃
B.这组数据的中位数是30
C.这组数据的众数是24
D.周四与周五的最高气温相差8℃
7.(2分)(2023 临川区校级一模)以下说法合理的是( )
A.小明做了3次掷图钉的实验,发现2次钉尖朝上,由此他说钉尖朝上的概率是
B.某彩票的中奖概率是5%,那么买100张彩票一定有5张中奖
C.某射击运动员射击一次只有两种可能的结果:中靶与不中靶,所以他击中靶的概率是
D.小明做了3次掷均匀硬币的实验,其中有一次正面朝上,2次正面朝下,他认为再掷一次,正面朝上的概率还是
8.(2分)(2023 武汉模拟)如图,有一电路AB是由图示的开关控制,闭合a,b,c,d,e五个开关中的任意两个开关,使电路形成通路,则使电路形成通路的概率是( )
A. B. C. D.
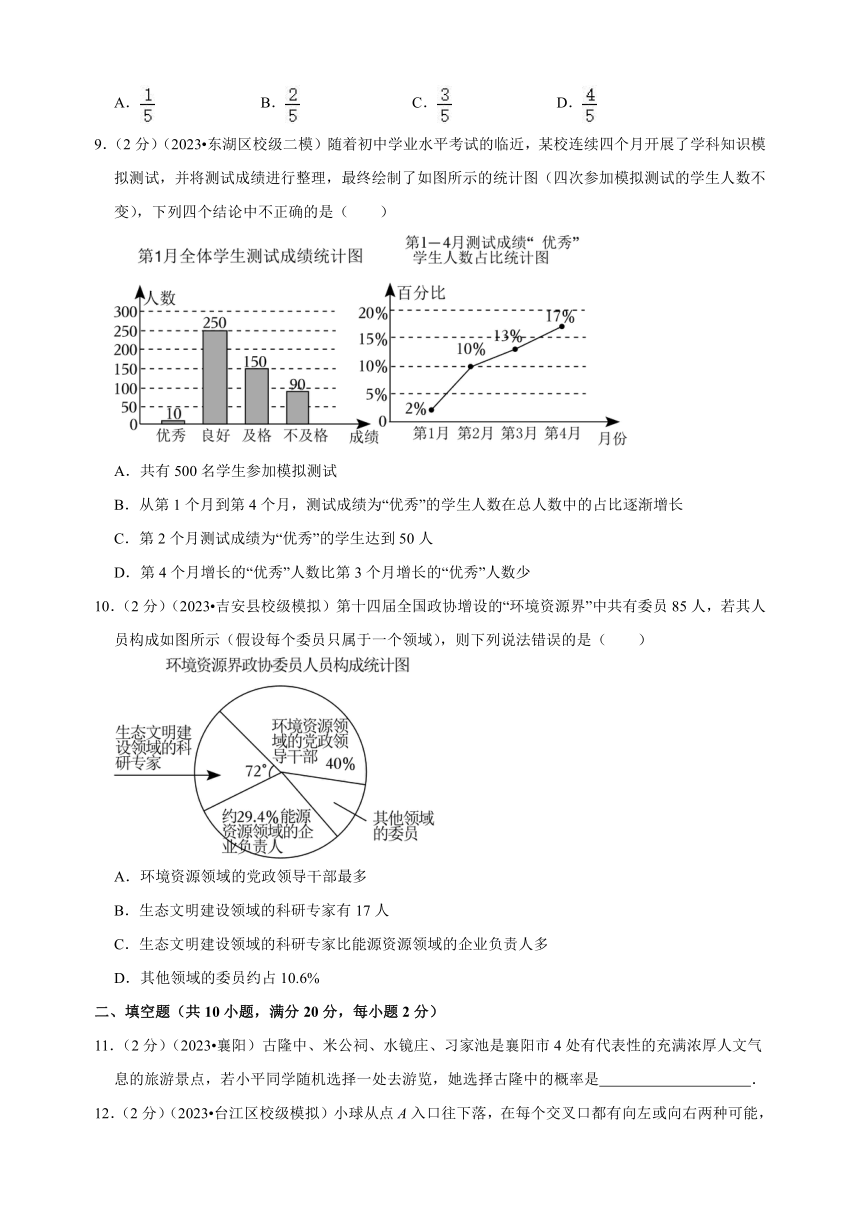
9.(2分)(2023 东湖区校级二模)随着初中学业水平考试的临近,某校连续四个月开展了学科知识模拟测试,并将测试成绩进行整理,最终绘制了如图所示的统计图(四次参加模拟测试的学生人数不变),下列四个结论中不正确的是( )
A.共有500名学生参加模拟测试
B.从第1个月到第4个月,测试成绩为“优秀”的学生人数在总人数中的占比逐渐增长
C.第2个月测试成绩为“优秀”的学生达到50人
D.第4个月增长的“优秀”人数比第3个月增长的“优秀”人数少
10.(2分)(2023 吉安县校级模拟)第十四届全国政协增设的“环境资源界”中共有委员85人,若其人员构成如图所示(假设每个委员只属于一个领域),则下列说法错误的是( )
A.环境资源领域的党政领导干部最多
B.生态文明建设领域的科研专家有17人
C.生态文明建设领域的科研专家比能源资源领域的企业负责人多
D.其他领域的委员约占10.6%
二、填空题(共10小题,满分20分,每小题2分)
11.(2分)(2023 襄阳)古隆中、米公祠、水镜庄、习家池是襄阳市4处有代表性的充满浓厚人文气息的旅游景点,若小平同学随机选择一处去游览,她选择古隆中的概率是 .
12.(2分)(2023 台江区校级模拟)小球从点A入口往下落,在每个交叉口都有向左或向右两种可能,且可能性相等.则小球最终从点E落出的概率为 .
13.(2分)(2023 镇平县三模)如图,两个相同的可以自由转动的转盘A和B,转盘A被二等分,分别标有数字﹣1,2;转盘B被三等分,分别标有数字3,0,﹣2.如果同时转动转盘A,B,转盘停止时,两个指针指向转盘A,B上的对应数字分别为x,y(当指针指在两个扇形的交线时,需重新转动转盘),那么点(x,y)落在平面直角坐标系第二象限的概率是 .
14.(2分)(2023 兴化市一模)当重复试验次数足够多时,可用频率来估计概率.历史上数学家皮尔进(Pearson)曾在实验中掷均匀的硬币24000次,正面朝上的次数是12012次,频率为0.5005,则掷一枚均匀的硬币,正面朝上的概率是 .
15.(2分)(2023 信阳二模)用图中两个可以自由转动的转盘做“配紫色”游戏,分别转动两个转盘,若其中一个转出红色,另一个转出蓝色即可配成紫色,则配成紫色的概率是 .
16.(2分)(2023 甘孜州)一天晚上,小张帮助妈妈清洗两个只有颜色不同的有盖茶杯,突然停电了,小张只好把杯盖和茶杯随机搭配在一起.则颜色搭配正确的概率是 .
17.(2分)(2023春 荣成市期中)“石头、剪子、布”是一个广为流传的游戏,规则是:甲、乙两人都做出“石头”“剪子”“布”3种手势中的1种,其中“石头”赢“剪子”,“剪子”赢“布”,“布”赢“石头”,手势相同不分输赢.假设甲、乙两人每次都随意并且同时做出3种手势中的1种,则乙不输的概率为 .
18.(2分)(2023 大连)一个不透明的口袋中有2个完全相同的小球,分别标号为1,2.随机摸出一个小球记录标号后放回,再随机摸出一个小球记录标号,两次摸出小球标号的和等于3的概率是 .
19.(2分)(2023 沭阳县二模)某学校为了增强学生体质,决定开放以下体育课外活动项目:A.篮球、B.乒乓球、C.跳绳、D.踢毽子.为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,其中A所在扇形的圆心角为30°,则在被调查的学生中选择跳绳的人数是 .
20.(2分)(2023春 江岸区校级月考)十八世纪法国的博物学家C 布丰做过一个有趣的投针试验.如图,在一个平面上画一组相距为d的平行线,用一根长度为l(l<d)的针任意投掷在这个平面上,针与直线相交的概率为,可以通过这一试验来估计π的近似值,某数学兴趣小组利用计算机模拟布丰投针试验,取l=,得到试验数据如下表:
试验次数 1500 2000 2500 3000 3500 4000 4500 5000
相交频数 495 623 799 954 1123 1269 1434 1590
相交频率 0.3300 0.3115 0.3196 0.3180 0.3209 0.3173 0.3187 0.3180
可以估计出针与直线相交的概率为 (精确到0.001),由此估计π的近似值为 (精确到0.001).
三、解答题(共8小题,满分60分)
21.(6分)(2023 通榆县二模)“航天知识竞赛”活动中,获得“小宇航员”称号的小颖得到了A,B,C,D四枚纪念章(除图案外完全相同),如图所示,四枚纪念章上分别印有“嫦娥五号”、“天问一号”、“长征火箭”和“天宫一号”的图案.她将这四枚纪念章背面朝上放在桌面上,然后从中一次随机选取两枚送给同学小彬,请用列表或画树状图的方法求小颖送给小彬的两枚纪念章中恰好有一枚印有“嫦娥五号”图案的概率.
(6分)(2023秋 道外区校级月考)2023男子篮球世界杯落下帷幕,中国男篮再一次无缘2024年巴黎奥运会,72中学篮球队针对此次失利,将失败原因分为五个选项:A.乔帅的用人不当,B.王哲林的关键失误,C.李凯尔没有发挥出应有的水平,D.缺少郭艾伦,E.姚主席制定的联赛规则有缺陷,对篮球队员进行调查,统计结果如图,请回答下列问题.
(1)此次调查的样本容量是 ,并补全条形统计图;
(2)扇形统计图中,A选项对应的百分比是 ,本次调查数据的中位数落在 小组内;
(3)若该中学有2000名学生,请你估计选B的同学大约有多少人?
23.(8分)(2023秋 武昌区月考)某校开展阳光体育运动,调查了七年级学生喜欢的球类活动(每人只选一项自己最喜欢的球类项目),并将调查情况制成如下统计表和统计图(不完整).请将统计表和统计图补充完整.
球类项目 乒乓球 篮球 足球 排球
喜欢人数/人 30人 人 人 人
24.(8分)(2023秋 蔡甸区月考)某校为了解学生参加家务劳动的情况,随机抽取了部分学生在某个休息日做家务的劳动时间t(单位:h)作为样本,将收集的数据整理后分为A,B,C,D,E五个组别,其中A组的数据分别为:0.5,0.4,0.3,0.4,0.3,绘制成如下不完整的统计图表.
各组劳动时间的频数分布表:
组别 时间t/h 频数
A 0<t≤0.5 5
B 0.5<t≤1 a
C 1<t≤1.5 20
D 1.5<t≤2 15
E t>2 8
请根据以上信息解答下列问题.
(1)A组数据的中位数是 ;
(2)本次调查的样本容量是 ,B组所在扇形的圆心角的大小是 ;
(3)若该校有2400名学生,估计该校学生劳动时间超过1h的人数.
25.(8分)(2023 东莞市一模)2022年虎年新春,中国女足3:2逆转韩国,时隔16年再夺亚洲杯总冠军:2022年国庆,中国女篮高歌猛进,时隔28年再夺世界杯亚军,展现了中国体育的风采!为了培养青少年体育兴趣、体育意识,某校初中开展了“阳光体育活动”,决定开设篮球、足球、乒乓球、羽毛球、排球这五项球类活动,为了了解学生对这五项活动的喜爱情况,随机调查了一些学生(每名学生必选且只能选择这五项活动中的一种).根据以下统计图提供的信息,请解答下列问题:
(1)本次被调查的学生有 名,补全条形统计图;
(2)扇形统计图中“羽毛球”对应的扇形的圆心角度数是 ;
(3)学校准备推荐甲、乙、丙、丁四名同学中的2名参加全市中学生篮球比赛,则甲和乙同学同时被选中的概率是多少?
26.(8分)(2023春 蓬安县期中)我县某学校根据《南充市中小学生课后服务实施意见》,积极开展课后延时服务活动,提供了“合唱,舞蹈,科创,书法,美术,课本剧,棋类……”等课程供学生自由选择.半学期后,该校为了解学生对课后延时服务的满意情况,随机对部分学生进行问卷调查,并将调查结果按照“A.满意;B.比较满意;C.基本满意;D.不满意”四个等级绘制成如图所示的两幅不完整统计图.
请根据图中信息,解答下列问题:
(1)将条形统计图补充完整;
(2)表示等级D的扇形的圆心角是 度;
(3)由于学校条件限制,“课本剧”课程仅剩下一个名额,而学生小华和小亮都想参加,他们决定采用抽纸牌的方法来确定,规则是:“将背面完全相同,正面分别标有数字1,2,3,4的四张牌洗匀后,背面朝上放置在桌面上,每人随机抽一次且一次只抽一张;一 人抽后记下数字,将牌放回洗匀背面朝上放置在桌面上,再由另一人抽.若小华抽得的数字比小亮抽得的数字大,名额给小华,否则给小亮.”请用画树状图或列表的方法计算出小华和小亮获得该名额的概率,并说明这个规则对双方是否公平.
27.(8分)(2023 开福区校级二模)某县教育局为了丰富初中学生的大课间活动,要求各学校开展形式多样的阳光体育活动.某中学就“学生体育活动兴趣爱好”的问题,随机调查了本校某班的学生,并根据调查结果绘制成如下的不完整的扇形统计图和条形统计图:
(1)在这次调查中,喜欢篮球项目的同学有 人,在扇形统计图中,“乒乓球”的百分比为 %,如果学校有800名学生,估计全校学生中有 人喜欢篮球项目.
(2)请将条形统计图补充完整.
(3)在被调查的学生中,喜欢篮球的有2名女同学,其余为男同学.现要从中随机抽取2名同学代表班级参加校篮球队,请直接写出所抽取的2名同学恰好是1名女同学和1名男同学的概率.
28.(8分)(2023 曹妃甸区模拟)在一个不透明的盒子里装有颜色不同的黑、白两种球共40个,小颖做摸球试验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是“摸到白色球”的频率折线统计图.
(1)请估计:当n很大时,摸到白球的概率将会接近 (精确到0.01),假如你摸一次,你摸到白球的概率为 ;
(2)试估算盒子里白、黑两种颜色的球各有多少个?
(3)在(2)条件下,如果要使摸到白球的概率为,需要往盒子里再放入多少个白球?
参考答案
一、选择题(共10小题,满分20分,每小题2分)
1.A
解:随机掷一枚均匀的硬币两次,可能的结果有:正正,正反,反正,反反,∴两次正面都朝上的概率是.故选:A.
2.C
解:“抛掷一枚均匀硬币,落地后正面朝上”这一事件是随机事件,故选:C.
3.D
解:根据题意可得,用来表示不同品种的奶牛的日平均产奶量最为合适的是条形统计图,因为条形统计图能很好反应不同品种奶牛的平均产量.故选:D.
4.C
解:A.企业招聘,对应聘人员进行面试,应进行全面调查,故此选项不合题意;
B.检测航天飞船的设备零件的质量情况,应进行全面调查,故此选项不合题意;
C.检测一批汽车轮胎的使用寿命,应进行抽样调查,故此选项符合题意;
D.全国人口普查,应进行全面调查,故此选项不合题意.
故选:C.
5.B
解:由频率分布图可知,当实验的次数逐渐增大时,摸到黄球的频率越稳定在0.6附近,
因此摸到黄球的概率为0.6,所以有=0.6,解得n=3,经检验,n=3是原方程的解,
故选:B.
6.B
解:A、由纵坐标看出,这一天中最高气温是32℃,说法正确,故A不符合题意;
B、这组数据的中位数是27,原说法错误,故B符合题意;
C、这组数据的众数是24,说法正确,故C不符合题意;
D、周四与周五的最高气温相差8℃,说法正确,故D不符合题意;
故选:B.
7.D
解:小明做了3次掷图钉的实验,发现2次钉尖朝上,由此他说钉尖朝上的概率是是错误的,3次试验不能总结出概率,故选项A错误,
某彩票的中奖概率是5%,那么买100张彩票可能有5张中奖,但不一定有5张中奖,故选项B错误,
某射击运动员射击一次只有两种可能的结果:中靶与不中靶,所以他击中靶的概率是不正确,中靶与不中靶不是等可能事件,故选项C错误,
小明做了3次掷均匀硬币的实验,其中有一次正面朝上,2次正面朝下,他认为再掷一次,正面朝上的可能性是,故选项D正确,
故选:D.
8.C
解:列表得:
(a,e) (b,e) (c,e) (d,e) ﹣
(a,d) (b,d) (c,d) ﹣ (e,d)
(a,c) (b,c) ﹣ (d,c) (e,c)
(a,b) ﹣ (c,b) (d,b) (e,b)
﹣ (b,a) (c,a) (d,a) (e,a)
∴一共有20种情况,使电路形成通路的有12种情况,∴使电路形成通路的概率是=,
故选:C.
9.D
解:A、测试的学生人数为:10+250+150+90=500(名),正确,故不符合题意;
B、由折线统计图可知,从第1周到第4周,测试成绩“优秀”的学生人数在总人数中的占比逐周增长,正确,故不符合题意;
C、第2月增长的“优秀”人数为500×10%=50(人),正确,故不符合题意;
D、第4月增长的“优秀”人数为500×17%﹣500×13%=20(人),第3月增长的“优秀”人数500×13%﹣500×10%=15(人),错误,故符合题意.
故选:D.
10.C
解:环境资源领域的党政领导干部:85×40%=34(人);
生态文明建设领域的科研专家有:85×=17(人);
能源资源领域的企业负责人:85×29.4%=24.99≈25(人);
领域的企业的委员:1﹣40%﹣20%﹣29.4%≈10%.
∴生态文明建设领域的科研专家比能源资源领域的企业负责人少;
故C选项错,
故选:C.
二、填空题(共10小题,满分20分,每小题2分)
11. .
解:古隆中、米公祠、水镜庄、习家池这4处有代表性的旅游景点,被抽到的可能性是均等的,共有4种等可能出现的结果,而选择古隆中的只有1种,所以选择古隆中的概率是,故答案为:.
12. .
解:由图可知,在每个交叉口都有向左或向右两种可能,且可能性相等,小球最终落出的点共有E、F、G、H四个,所以,最终从点E落出的概率为.故答案为:.
13. .
解:列表如下:
﹣1 2
3 ﹣1,3 2,3
0 ﹣1,0 2,0
﹣2 ﹣1,﹣2 2,﹣2
由表可知,共有6种等可能结果,其中点(x,y)落在直角坐标系第二象限的有1种,
所以点(x,y)落在直角坐标系第二象限的概率是,
故答案为:.
14. 0.5005
解:当重复试验次数足够多时,频率为0.5005,∴掷一枚均匀的硬币,正面朝上的概率是0.5005.
故答案为:0.5005.
15.
解:画树状图如下:
共有12种等可能的结果,其中配成紫色的结果有4种,∴配成紫色的概率为=,故答案为:.
16.
解:用A和a分别表示第一个有盖茶杯的杯盖和茶杯;
用B和b分别表示第二个有盖茶杯的杯盖和茶杯、经过搭配所能产生的结果如下:
所以颜色搭配正确的概率是=.
故答案为:.
17.
解:画树状图为:共有9种等可能的结果数,乙不输的结果数有6种,所以乙不输的概率的概率.
故答案为:.
18.
解:画树状图如下:
一共有4种等可能的情况,其中两次摸出小球标号的和等于3有2种可能,
∴P(两次摸出小球标号的和等于3)=,
故答案为:.
19. 100人
解:由题意可得,
被调查的学生有:20÷=240(人),
则选择跳绳的有:240﹣20﹣80﹣40=100(人),
故答案为:100人.
20. 0.318 3.145
解:根据试验数据得:当试验次数逐渐增大时,相交频率接近与0.318,
∴相交的概率为0.318;
∵,
∴,
∴,
解得:π≈3.145,
故答案为:0.318;3.145.
三、解答题(共8小题,满分60分)
21.
解:画树状图如下:
共有12种可能的结果,其中符合条件的结果有6种,
∴小颖送给小彬的两枚纪念章中恰好有一枚印有“嫦娥五号”图案的概率为 .
22.
解:(1)样本容量为:13÷26%=50,
故答案为:50;
B组人数为:50﹣5﹣13﹣20﹣2=10(人),
补全条形统计图如下:
(2)A选项对应的百分比是:,
∵一共有50个数据,第25,26个数据在C组,
∴本次调查数据的中位数落在C小组内,
故答案为:10%,C;
(3)2000×=400(人),
答:估计选B的同学大约有400人.
23.
解:由题意得,七年级学生人数为:30÷25%=120(人),
故篮球人数为:120×30%=36(人),排球人数为:120×12.5%=15(人),
所以足球人数为:120﹣30﹣36﹣15=39(人),
故足球所占百分比为:=32.5%.
故答案为:36,39,15.
24.
解:(1)∵A组的数据分别为:0.5,0.4,0.4,0.3,0.3,
∴A组数据的中位数是0.4;
故答案为:0.4;
(2)本次调查的样本容量是15÷25%=60,
∵a=60﹣5﹣20﹣15﹣8=12,
∴B组所在扇形的圆心角的大小是360°×=72°,
故答案为:60,72°;
(3)2400×=1720(人),
答:估计该校学生劳动时间超过lh的大约有1720人.
25.
解:(1)本次被调查的学生人数为30÷30%=100(名).
选择“足球”的人数为35%×100=35(名).
补全条形统计图如下:
故答案为:100;
(2)扇形统计图中“羽毛球”对应的扇形的圆心角度数为 ×360°=36°.
故答案为:36°.
(3)画树状图如下:
共有12种等可能的结果,其中甲和乙同学同时被选中的结果有2种,
∴甲和乙同学同时被选中的概率为=.
26.
解:(1)调查的总人数是:15÷25%=60(人),
B等级的人数有:60﹣15﹣10﹣10=25(人),
补全统计图如下:
(2)等级D的扇形的圆心角是:360°×=60°;
故答案为:60;
(3)根据题意画图如下:
共有16种等可能的情况数,其中小华抽得的数字比小亮抽得的数字大的情况有6种,
则名额给小华的概率是=,名额给小亮的概率是,
∵<,
∴这个规则对双方不公平.
27.
解:(1)调查的总人数为20÷40%=50(人),
所以喜欢篮球项目的同学的人数=50﹣20﹣10﹣15=5(人);
“乒乓球”的百分比=×100%=20%,
因为800××100%=80,
所以估计全校学生中有80人喜欢篮球项目;
故答案为5,20,80;
(2)如图,
(3)画树状图为:
共有20种等可能的结果数,其中所抽取的2名同学恰好是1名女同学和1名男同学的结果数为12,
所以所抽取的2名同学恰好是1名女同学和1名男同学的概率==.
28.
解:(1)根据题意得:当n很大时,摸到白球的概率将会接近0.50;假如你摸一次,你摸到白球的概率为0.5;
(2)40×0.5=20(个),40﹣20=20(个);
答:估算盒子里白、黑两种颜色的球分别有20个、20个;
(3)设需要往盒子里再放入x个白球;
根据题意得:=,
解得:x=10;
答:需要往盒子里再放入10个白球。
第8章《统计和概率的简单应用》
考试时间:120分钟,试卷满分:100分
姓名:_________ 班级:_________ 学号:_________
一、选择题(共10小题,满分20分,每小题2分)
1.(2分)(2013春 建湖县校级月考)随机掷一枚均匀的硬币两次,两次正面都朝上的概率是( )
A. B. C. D.1
2.(2分)(2021 张店区二模)“抛掷一枚均匀硬币,落地后正面朝上”这一事件是( )
A.确定事件 B.必然事件 C.随机事件 D.不可能事件
3.(2分)(2023 定远县校级三模)下列四个统计图中,用来表示不同品种的奶牛的日平均产奶量最为合适的是( )
A. B.
C. D.
4.(2分)(2023 镇江二模)下列调查适合抽样调查的是( )
A.企业招聘,对应聘人员进行面试
B.检测航天飞船的设备零件的质量情况
C.检测一批汽车轮胎的使用寿命
D.全国人口普查
5.(2分)(2023 蚌山区一模)在一个不透明的口袋中,放置6个黄球、1个红球和n个蓝球,这些小球除颜色外其余均相同,课外兴趣小组每次摸出一个球记录下颜色后再放回,并且统计了黄球出现的频率,如图,则n的值是( )
A.2 B.3 C.5 D.8
6.(2分)(2023 长沙)长沙市某一周内每日最高气温情况如图所示,下列说法中,错误的是( )
A.这周最高气温是32℃
B.这组数据的中位数是30
C.这组数据的众数是24
D.周四与周五的最高气温相差8℃
7.(2分)(2023 临川区校级一模)以下说法合理的是( )
A.小明做了3次掷图钉的实验,发现2次钉尖朝上,由此他说钉尖朝上的概率是
B.某彩票的中奖概率是5%,那么买100张彩票一定有5张中奖
C.某射击运动员射击一次只有两种可能的结果:中靶与不中靶,所以他击中靶的概率是
D.小明做了3次掷均匀硬币的实验,其中有一次正面朝上,2次正面朝下,他认为再掷一次,正面朝上的概率还是
8.(2分)(2023 武汉模拟)如图,有一电路AB是由图示的开关控制,闭合a,b,c,d,e五个开关中的任意两个开关,使电路形成通路,则使电路形成通路的概率是( )
A. B. C. D.
9.(2分)(2023 东湖区校级二模)随着初中学业水平考试的临近,某校连续四个月开展了学科知识模拟测试,并将测试成绩进行整理,最终绘制了如图所示的统计图(四次参加模拟测试的学生人数不变),下列四个结论中不正确的是( )
A.共有500名学生参加模拟测试
B.从第1个月到第4个月,测试成绩为“优秀”的学生人数在总人数中的占比逐渐增长
C.第2个月测试成绩为“优秀”的学生达到50人
D.第4个月增长的“优秀”人数比第3个月增长的“优秀”人数少
10.(2分)(2023 吉安县校级模拟)第十四届全国政协增设的“环境资源界”中共有委员85人,若其人员构成如图所示(假设每个委员只属于一个领域),则下列说法错误的是( )
A.环境资源领域的党政领导干部最多
B.生态文明建设领域的科研专家有17人
C.生态文明建设领域的科研专家比能源资源领域的企业负责人多
D.其他领域的委员约占10.6%
二、填空题(共10小题,满分20分,每小题2分)
11.(2分)(2023 襄阳)古隆中、米公祠、水镜庄、习家池是襄阳市4处有代表性的充满浓厚人文气息的旅游景点,若小平同学随机选择一处去游览,她选择古隆中的概率是 .
12.(2分)(2023 台江区校级模拟)小球从点A入口往下落,在每个交叉口都有向左或向右两种可能,且可能性相等.则小球最终从点E落出的概率为 .
13.(2分)(2023 镇平县三模)如图,两个相同的可以自由转动的转盘A和B,转盘A被二等分,分别标有数字﹣1,2;转盘B被三等分,分别标有数字3,0,﹣2.如果同时转动转盘A,B,转盘停止时,两个指针指向转盘A,B上的对应数字分别为x,y(当指针指在两个扇形的交线时,需重新转动转盘),那么点(x,y)落在平面直角坐标系第二象限的概率是 .
14.(2分)(2023 兴化市一模)当重复试验次数足够多时,可用频率来估计概率.历史上数学家皮尔进(Pearson)曾在实验中掷均匀的硬币24000次,正面朝上的次数是12012次,频率为0.5005,则掷一枚均匀的硬币,正面朝上的概率是 .
15.(2分)(2023 信阳二模)用图中两个可以自由转动的转盘做“配紫色”游戏,分别转动两个转盘,若其中一个转出红色,另一个转出蓝色即可配成紫色,则配成紫色的概率是 .
16.(2分)(2023 甘孜州)一天晚上,小张帮助妈妈清洗两个只有颜色不同的有盖茶杯,突然停电了,小张只好把杯盖和茶杯随机搭配在一起.则颜色搭配正确的概率是 .
17.(2分)(2023春 荣成市期中)“石头、剪子、布”是一个广为流传的游戏,规则是:甲、乙两人都做出“石头”“剪子”“布”3种手势中的1种,其中“石头”赢“剪子”,“剪子”赢“布”,“布”赢“石头”,手势相同不分输赢.假设甲、乙两人每次都随意并且同时做出3种手势中的1种,则乙不输的概率为 .
18.(2分)(2023 大连)一个不透明的口袋中有2个完全相同的小球,分别标号为1,2.随机摸出一个小球记录标号后放回,再随机摸出一个小球记录标号,两次摸出小球标号的和等于3的概率是 .
19.(2分)(2023 沭阳县二模)某学校为了增强学生体质,决定开放以下体育课外活动项目:A.篮球、B.乒乓球、C.跳绳、D.踢毽子.为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,其中A所在扇形的圆心角为30°,则在被调查的学生中选择跳绳的人数是 .
20.(2分)(2023春 江岸区校级月考)十八世纪法国的博物学家C 布丰做过一个有趣的投针试验.如图,在一个平面上画一组相距为d的平行线,用一根长度为l(l<d)的针任意投掷在这个平面上,针与直线相交的概率为,可以通过这一试验来估计π的近似值,某数学兴趣小组利用计算机模拟布丰投针试验,取l=,得到试验数据如下表:
试验次数 1500 2000 2500 3000 3500 4000 4500 5000
相交频数 495 623 799 954 1123 1269 1434 1590
相交频率 0.3300 0.3115 0.3196 0.3180 0.3209 0.3173 0.3187 0.3180
可以估计出针与直线相交的概率为 (精确到0.001),由此估计π的近似值为 (精确到0.001).
三、解答题(共8小题,满分60分)
21.(6分)(2023 通榆县二模)“航天知识竞赛”活动中,获得“小宇航员”称号的小颖得到了A,B,C,D四枚纪念章(除图案外完全相同),如图所示,四枚纪念章上分别印有“嫦娥五号”、“天问一号”、“长征火箭”和“天宫一号”的图案.她将这四枚纪念章背面朝上放在桌面上,然后从中一次随机选取两枚送给同学小彬,请用列表或画树状图的方法求小颖送给小彬的两枚纪念章中恰好有一枚印有“嫦娥五号”图案的概率.
(6分)(2023秋 道外区校级月考)2023男子篮球世界杯落下帷幕,中国男篮再一次无缘2024年巴黎奥运会,72中学篮球队针对此次失利,将失败原因分为五个选项:A.乔帅的用人不当,B.王哲林的关键失误,C.李凯尔没有发挥出应有的水平,D.缺少郭艾伦,E.姚主席制定的联赛规则有缺陷,对篮球队员进行调查,统计结果如图,请回答下列问题.
(1)此次调查的样本容量是 ,并补全条形统计图;
(2)扇形统计图中,A选项对应的百分比是 ,本次调查数据的中位数落在 小组内;
(3)若该中学有2000名学生,请你估计选B的同学大约有多少人?
23.(8分)(2023秋 武昌区月考)某校开展阳光体育运动,调查了七年级学生喜欢的球类活动(每人只选一项自己最喜欢的球类项目),并将调查情况制成如下统计表和统计图(不完整).请将统计表和统计图补充完整.
球类项目 乒乓球 篮球 足球 排球
喜欢人数/人 30人 人 人 人
24.(8分)(2023秋 蔡甸区月考)某校为了解学生参加家务劳动的情况,随机抽取了部分学生在某个休息日做家务的劳动时间t(单位:h)作为样本,将收集的数据整理后分为A,B,C,D,E五个组别,其中A组的数据分别为:0.5,0.4,0.3,0.4,0.3,绘制成如下不完整的统计图表.
各组劳动时间的频数分布表:
组别 时间t/h 频数
A 0<t≤0.5 5
B 0.5<t≤1 a
C 1<t≤1.5 20
D 1.5<t≤2 15
E t>2 8
请根据以上信息解答下列问题.
(1)A组数据的中位数是 ;
(2)本次调查的样本容量是 ,B组所在扇形的圆心角的大小是 ;
(3)若该校有2400名学生,估计该校学生劳动时间超过1h的人数.
25.(8分)(2023 东莞市一模)2022年虎年新春,中国女足3:2逆转韩国,时隔16年再夺亚洲杯总冠军:2022年国庆,中国女篮高歌猛进,时隔28年再夺世界杯亚军,展现了中国体育的风采!为了培养青少年体育兴趣、体育意识,某校初中开展了“阳光体育活动”,决定开设篮球、足球、乒乓球、羽毛球、排球这五项球类活动,为了了解学生对这五项活动的喜爱情况,随机调查了一些学生(每名学生必选且只能选择这五项活动中的一种).根据以下统计图提供的信息,请解答下列问题:
(1)本次被调查的学生有 名,补全条形统计图;
(2)扇形统计图中“羽毛球”对应的扇形的圆心角度数是 ;
(3)学校准备推荐甲、乙、丙、丁四名同学中的2名参加全市中学生篮球比赛,则甲和乙同学同时被选中的概率是多少?
26.(8分)(2023春 蓬安县期中)我县某学校根据《南充市中小学生课后服务实施意见》,积极开展课后延时服务活动,提供了“合唱,舞蹈,科创,书法,美术,课本剧,棋类……”等课程供学生自由选择.半学期后,该校为了解学生对课后延时服务的满意情况,随机对部分学生进行问卷调查,并将调查结果按照“A.满意;B.比较满意;C.基本满意;D.不满意”四个等级绘制成如图所示的两幅不完整统计图.
请根据图中信息,解答下列问题:
(1)将条形统计图补充完整;
(2)表示等级D的扇形的圆心角是 度;
(3)由于学校条件限制,“课本剧”课程仅剩下一个名额,而学生小华和小亮都想参加,他们决定采用抽纸牌的方法来确定,规则是:“将背面完全相同,正面分别标有数字1,2,3,4的四张牌洗匀后,背面朝上放置在桌面上,每人随机抽一次且一次只抽一张;一 人抽后记下数字,将牌放回洗匀背面朝上放置在桌面上,再由另一人抽.若小华抽得的数字比小亮抽得的数字大,名额给小华,否则给小亮.”请用画树状图或列表的方法计算出小华和小亮获得该名额的概率,并说明这个规则对双方是否公平.
27.(8分)(2023 开福区校级二模)某县教育局为了丰富初中学生的大课间活动,要求各学校开展形式多样的阳光体育活动.某中学就“学生体育活动兴趣爱好”的问题,随机调查了本校某班的学生,并根据调查结果绘制成如下的不完整的扇形统计图和条形统计图:
(1)在这次调查中,喜欢篮球项目的同学有 人,在扇形统计图中,“乒乓球”的百分比为 %,如果学校有800名学生,估计全校学生中有 人喜欢篮球项目.
(2)请将条形统计图补充完整.
(3)在被调查的学生中,喜欢篮球的有2名女同学,其余为男同学.现要从中随机抽取2名同学代表班级参加校篮球队,请直接写出所抽取的2名同学恰好是1名女同学和1名男同学的概率.
28.(8分)(2023 曹妃甸区模拟)在一个不透明的盒子里装有颜色不同的黑、白两种球共40个,小颖做摸球试验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是“摸到白色球”的频率折线统计图.
(1)请估计:当n很大时,摸到白球的概率将会接近 (精确到0.01),假如你摸一次,你摸到白球的概率为 ;
(2)试估算盒子里白、黑两种颜色的球各有多少个?
(3)在(2)条件下,如果要使摸到白球的概率为,需要往盒子里再放入多少个白球?
参考答案
一、选择题(共10小题,满分20分,每小题2分)
1.A
解:随机掷一枚均匀的硬币两次,可能的结果有:正正,正反,反正,反反,∴两次正面都朝上的概率是.故选:A.
2.C
解:“抛掷一枚均匀硬币,落地后正面朝上”这一事件是随机事件,故选:C.
3.D
解:根据题意可得,用来表示不同品种的奶牛的日平均产奶量最为合适的是条形统计图,因为条形统计图能很好反应不同品种奶牛的平均产量.故选:D.
4.C
解:A.企业招聘,对应聘人员进行面试,应进行全面调查,故此选项不合题意;
B.检测航天飞船的设备零件的质量情况,应进行全面调查,故此选项不合题意;
C.检测一批汽车轮胎的使用寿命,应进行抽样调查,故此选项符合题意;
D.全国人口普查,应进行全面调查,故此选项不合题意.
故选:C.
5.B
解:由频率分布图可知,当实验的次数逐渐增大时,摸到黄球的频率越稳定在0.6附近,
因此摸到黄球的概率为0.6,所以有=0.6,解得n=3,经检验,n=3是原方程的解,
故选:B.
6.B
解:A、由纵坐标看出,这一天中最高气温是32℃,说法正确,故A不符合题意;
B、这组数据的中位数是27,原说法错误,故B符合题意;
C、这组数据的众数是24,说法正确,故C不符合题意;
D、周四与周五的最高气温相差8℃,说法正确,故D不符合题意;
故选:B.
7.D
解:小明做了3次掷图钉的实验,发现2次钉尖朝上,由此他说钉尖朝上的概率是是错误的,3次试验不能总结出概率,故选项A错误,
某彩票的中奖概率是5%,那么买100张彩票可能有5张中奖,但不一定有5张中奖,故选项B错误,
某射击运动员射击一次只有两种可能的结果:中靶与不中靶,所以他击中靶的概率是不正确,中靶与不中靶不是等可能事件,故选项C错误,
小明做了3次掷均匀硬币的实验,其中有一次正面朝上,2次正面朝下,他认为再掷一次,正面朝上的可能性是,故选项D正确,
故选:D.
8.C
解:列表得:
(a,e) (b,e) (c,e) (d,e) ﹣
(a,d) (b,d) (c,d) ﹣ (e,d)
(a,c) (b,c) ﹣ (d,c) (e,c)
(a,b) ﹣ (c,b) (d,b) (e,b)
﹣ (b,a) (c,a) (d,a) (e,a)
∴一共有20种情况,使电路形成通路的有12种情况,∴使电路形成通路的概率是=,
故选:C.
9.D
解:A、测试的学生人数为:10+250+150+90=500(名),正确,故不符合题意;
B、由折线统计图可知,从第1周到第4周,测试成绩“优秀”的学生人数在总人数中的占比逐周增长,正确,故不符合题意;
C、第2月增长的“优秀”人数为500×10%=50(人),正确,故不符合题意;
D、第4月增长的“优秀”人数为500×17%﹣500×13%=20(人),第3月增长的“优秀”人数500×13%﹣500×10%=15(人),错误,故符合题意.
故选:D.
10.C
解:环境资源领域的党政领导干部:85×40%=34(人);
生态文明建设领域的科研专家有:85×=17(人);
能源资源领域的企业负责人:85×29.4%=24.99≈25(人);
领域的企业的委员:1﹣40%﹣20%﹣29.4%≈10%.
∴生态文明建设领域的科研专家比能源资源领域的企业负责人少;
故C选项错,
故选:C.
二、填空题(共10小题,满分20分,每小题2分)
11. .
解:古隆中、米公祠、水镜庄、习家池这4处有代表性的旅游景点,被抽到的可能性是均等的,共有4种等可能出现的结果,而选择古隆中的只有1种,所以选择古隆中的概率是,故答案为:.
12. .
解:由图可知,在每个交叉口都有向左或向右两种可能,且可能性相等,小球最终落出的点共有E、F、G、H四个,所以,最终从点E落出的概率为.故答案为:.
13. .
解:列表如下:
﹣1 2
3 ﹣1,3 2,3
0 ﹣1,0 2,0
﹣2 ﹣1,﹣2 2,﹣2
由表可知,共有6种等可能结果,其中点(x,y)落在直角坐标系第二象限的有1种,
所以点(x,y)落在直角坐标系第二象限的概率是,
故答案为:.
14. 0.5005
解:当重复试验次数足够多时,频率为0.5005,∴掷一枚均匀的硬币,正面朝上的概率是0.5005.
故答案为:0.5005.
15.
解:画树状图如下:
共有12种等可能的结果,其中配成紫色的结果有4种,∴配成紫色的概率为=,故答案为:.
16.
解:用A和a分别表示第一个有盖茶杯的杯盖和茶杯;
用B和b分别表示第二个有盖茶杯的杯盖和茶杯、经过搭配所能产生的结果如下:
所以颜色搭配正确的概率是=.
故答案为:.
17.
解:画树状图为:共有9种等可能的结果数,乙不输的结果数有6种,所以乙不输的概率的概率.
故答案为:.
18.
解:画树状图如下:
一共有4种等可能的情况,其中两次摸出小球标号的和等于3有2种可能,
∴P(两次摸出小球标号的和等于3)=,
故答案为:.
19. 100人
解:由题意可得,
被调查的学生有:20÷=240(人),
则选择跳绳的有:240﹣20﹣80﹣40=100(人),
故答案为:100人.
20. 0.318 3.145
解:根据试验数据得:当试验次数逐渐增大时,相交频率接近与0.318,
∴相交的概率为0.318;
∵,
∴,
∴,
解得:π≈3.145,
故答案为:0.318;3.145.
三、解答题(共8小题,满分60分)
21.
解:画树状图如下:
共有12种可能的结果,其中符合条件的结果有6种,
∴小颖送给小彬的两枚纪念章中恰好有一枚印有“嫦娥五号”图案的概率为 .
22.
解:(1)样本容量为:13÷26%=50,
故答案为:50;
B组人数为:50﹣5﹣13﹣20﹣2=10(人),
补全条形统计图如下:
(2)A选项对应的百分比是:,
∵一共有50个数据,第25,26个数据在C组,
∴本次调查数据的中位数落在C小组内,
故答案为:10%,C;
(3)2000×=400(人),
答:估计选B的同学大约有400人.
23.
解:由题意得,七年级学生人数为:30÷25%=120(人),
故篮球人数为:120×30%=36(人),排球人数为:120×12.5%=15(人),
所以足球人数为:120﹣30﹣36﹣15=39(人),
故足球所占百分比为:=32.5%.
故答案为:36,39,15.
24.
解:(1)∵A组的数据分别为:0.5,0.4,0.4,0.3,0.3,
∴A组数据的中位数是0.4;
故答案为:0.4;
(2)本次调查的样本容量是15÷25%=60,
∵a=60﹣5﹣20﹣15﹣8=12,
∴B组所在扇形的圆心角的大小是360°×=72°,
故答案为:60,72°;
(3)2400×=1720(人),
答:估计该校学生劳动时间超过lh的大约有1720人.
25.
解:(1)本次被调查的学生人数为30÷30%=100(名).
选择“足球”的人数为35%×100=35(名).
补全条形统计图如下:
故答案为:100;
(2)扇形统计图中“羽毛球”对应的扇形的圆心角度数为 ×360°=36°.
故答案为:36°.
(3)画树状图如下:
共有12种等可能的结果,其中甲和乙同学同时被选中的结果有2种,
∴甲和乙同学同时被选中的概率为=.
26.
解:(1)调查的总人数是:15÷25%=60(人),
B等级的人数有:60﹣15﹣10﹣10=25(人),
补全统计图如下:
(2)等级D的扇形的圆心角是:360°×=60°;
故答案为:60;
(3)根据题意画图如下:
共有16种等可能的情况数,其中小华抽得的数字比小亮抽得的数字大的情况有6种,
则名额给小华的概率是=,名额给小亮的概率是,
∵<,
∴这个规则对双方不公平.
27.
解:(1)调查的总人数为20÷40%=50(人),
所以喜欢篮球项目的同学的人数=50﹣20﹣10﹣15=5(人);
“乒乓球”的百分比=×100%=20%,
因为800××100%=80,
所以估计全校学生中有80人喜欢篮球项目;
故答案为5,20,80;
(2)如图,
(3)画树状图为:
共有20种等可能的结果数,其中所抽取的2名同学恰好是1名女同学和1名男同学的结果数为12,
所以所抽取的2名同学恰好是1名女同学和1名男同学的概率==.
28.
解:(1)根据题意得:当n很大时,摸到白球的概率将会接近0.50;假如你摸一次,你摸到白球的概率为0.5;
(2)40×0.5=20(个),40﹣20=20(个);
答:估算盒子里白、黑两种颜色的球分别有20个、20个;
(3)设需要往盒子里再放入x个白球;
根据题意得:=,
解得:x=10;
答:需要往盒子里再放入10个白球。
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
