18.2.3正方形同步练习(含答案)2023—2024学年人教版数学八年级下册
文档属性
| 名称 | 18.2.3正方形同步练习(含答案)2023—2024学年人教版数学八年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 279.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-22 13:57:13 | ||
图片预览


文档简介
18.2.3正方形同步练习2023—2024学年人教版数学八年级下册
一.选择题(共12小题)
1.下列说法中,正确的是( )
A.一组对边平行的四边形是平行四边形
B.有一个角是直角的四边形是矩形
C.四条边相等的四边形是菱形
D.对角线互相垂直平分的四边形是正方形
2.四边形ABCD的对角线AC、BD交于点O,有下列论断:
①AB=BC;②∠DAB=90°;③BO=DO,AO=CO;
④矩形ABCD;⑤菱形ABCD;⑥正方形ABCD.
其中推理不正确的是( )
A. B. C. D.
3.已知四边形ABCD是平行四边形,再从①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD四个条件中,选两个作为补充条件后,使得四边形ABCD是正方形,现有下列四种选法,其中不正确的是( )
A.①② B.②③ C.①③ D.②④
4.下列是关于某个四边形的三个结论:①它的对角线互相垂直;②它是一个正方形;③它是一个菱形.下列推理过程正确的是( )
A.由②推出③,由③推出① B.由①推出②,由②推出③
C.由③推出①,由①推出③ D.由①推出③,由③推出②
5.如图,在正方形ABCD中,点F为AB上一点,CF与BD交于点E,连接AE,若∠BCF=20°,则∠AEF为( )
A.35° B.40° C.45° D.50°
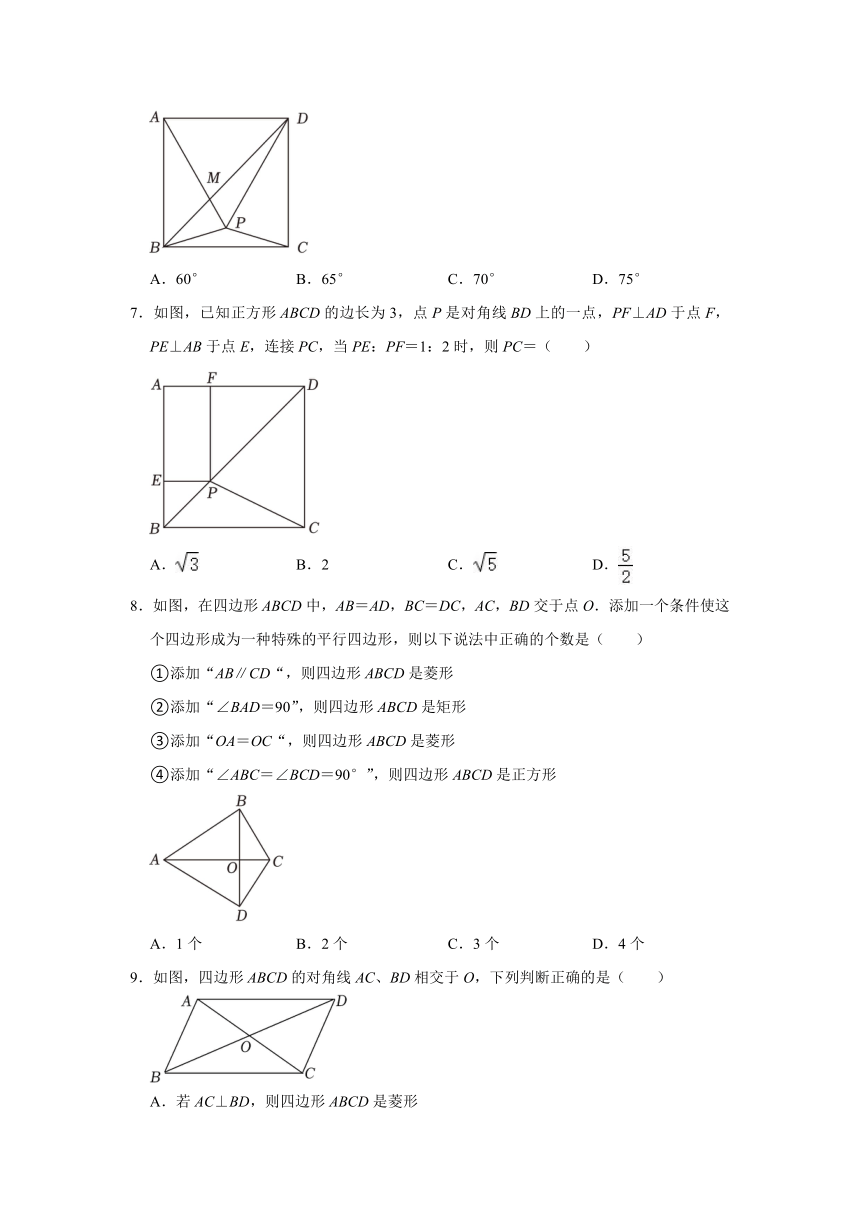
6.如图,在正方形ABCD内有一点P,PA=AB,PB=PC,若对角线BD与AP交于点M,则∠AMD的度数为( )
A.60° B.65° C.70° D.75°
7.如图,已知正方形ABCD的边长为3,点P是对角线BD上的一点,PF⊥AD于点F,PE⊥AB于点E,连接PC,当PE:PF=1:2时,则PC=( )
A. B.2 C. D.
8.如图,在四边形ABCD中,AB=AD,BC=DC,AC,BD交于点O.添加一个条件使这个四边形成为一种特殊的平行四边形,则以下说法中正确的个数是( )
①添加“AB∥CD“,则四边形ABCD是菱形
②添加“∠BAD=90”,则四边形ABCD是矩形
③添加“OA=OC“,则四边形ABCD是菱形
④添加“∠ABC=∠BCD=90°”,则四边形ABCD是正方形
A.1个 B.2个 C.3个 D.4个
9.如图,四边形ABCD的对角线AC、BD相交于O,下列判断正确的是( )
A.若AC⊥BD,则四边形ABCD是菱形
B.若AC=BD,则四边形ABCD是矩形
C.若AC⊥BD,AC=BD,则四边形ABCD是正方形
D.若AO=OC,BO=OD,则四边形ABCD是平行四边形
10.如图,四边形ABCD是平行四边形,下列结论中错误的是( )
A.当 ABCD是矩形时,∠ABC=90°
B.当 ABCD是菱形时,AC⊥BD
C.当 ABCD是正方形时,AC=BD
D.当 ABCD是菱形时,AB=AC
11.将图1中两个三角形按图2所示的方式摆放,其中四边形ABCD为矩形,连接PQ,MN,甲、乙两人有如下结论:
甲:若四边形ABCD为正方形,则四边形PQMN必是正方形;
乙:若四边形PQMN为正方形,则四边形ABCD必是正方形.
下列判断正确的是( )
A.甲正确,乙不正确 B.甲不正确,乙正确
C.甲、乙都不正确 D.甲、乙都正确
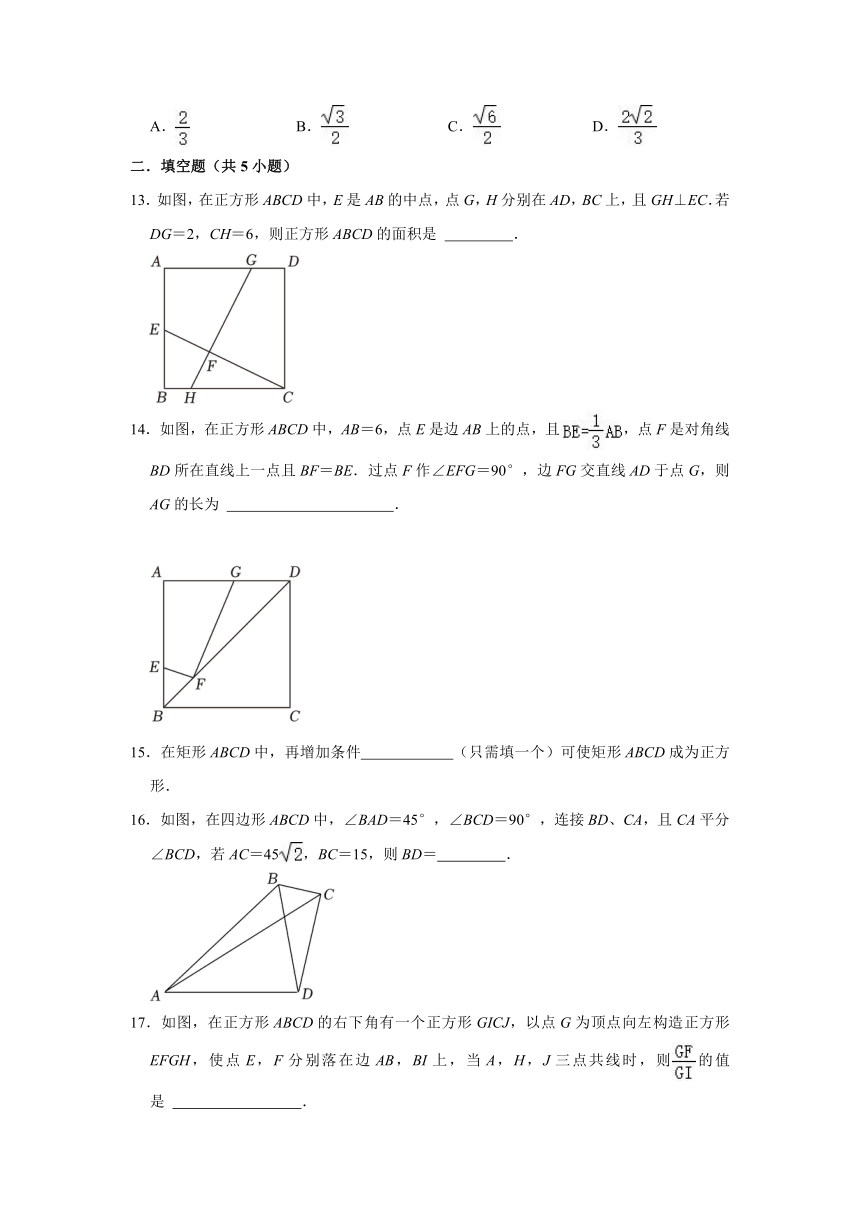
12.如图,在△ABC中,∠BAC=45°,AD⊥BC于点D.点E,F是AD上两点,且DE=DB,DF=DC,若BD=2,CD=3.则的值为( )
A. B. C. D.
二.填空题(共5小题)
13.如图,在正方形ABCD中,E是AB的中点,点G,H分别在AD,BC上,且GH⊥EC.若DG=2,CH=6,则正方形ABCD的面积是 .
14.如图,在正方形ABCD中,AB=6,点E是边AB上的点,且,点F是对角线BD所在直线上一点且BF=BE.过点F作∠EFG=90°,边FG交直线AD于点G,则AG的长为 .
15.在矩形ABCD中,再增加条件 (只需填一个)可使矩形ABCD成为正方形.
16.如图,在四边形ABCD中,∠BAD=45°,∠BCD=90°,连接BD、CA,且CA平分∠BCD,若AC=45,BC=15,则BD= .
17.如图,在正方形ABCD的右下角有一个正方形GICJ,以点G为顶点向左构造正方形EFGH,使点E,F分别落在边AB,BI上,当A,H,J三点共线时,则的值是 .
三.解答题(共5小题)
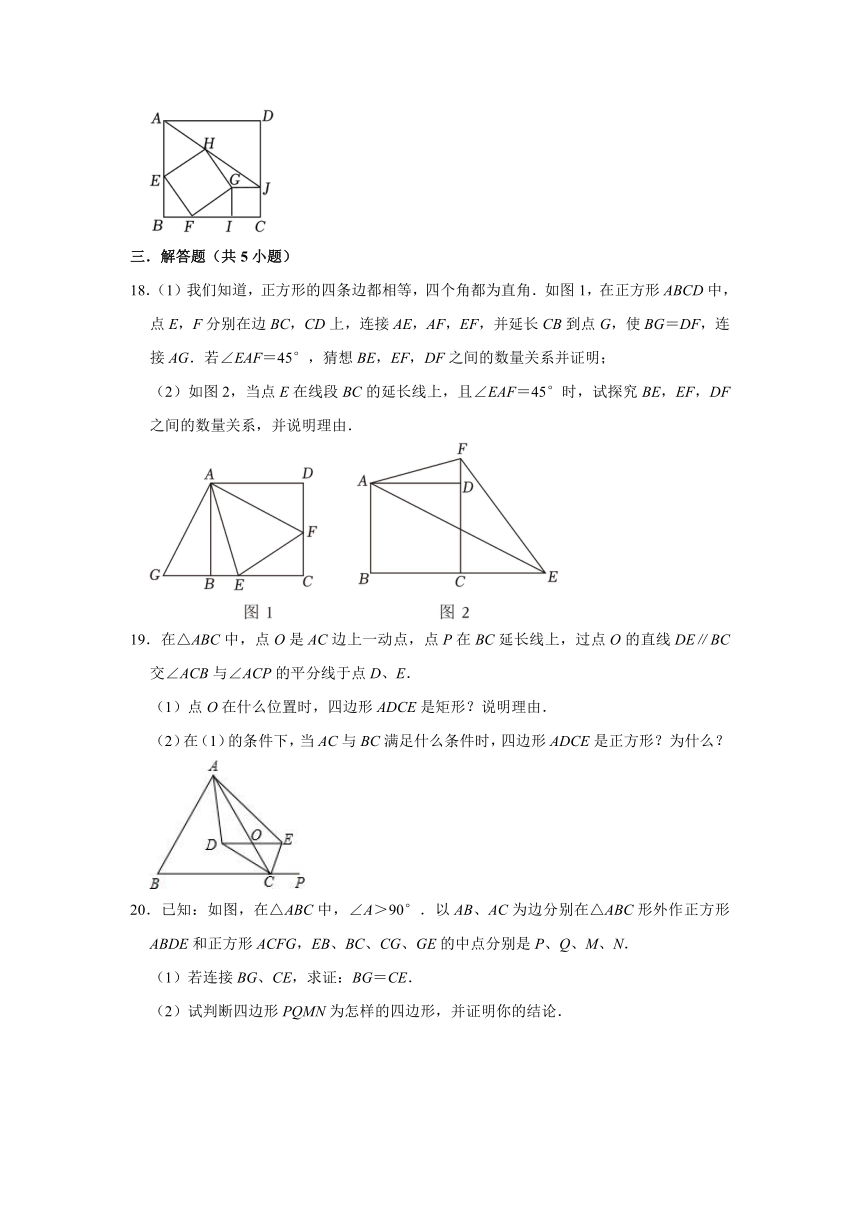
18.(1)我们知道,正方形的四条边都相等,四个角都为直角.如图1,在正方形ABCD中,点E,F分别在边BC,CD上,连接AE,AF,EF,并延长CB到点G,使BG=DF,连接AG.若∠EAF=45°,猜想BE,EF,DF之间的数量关系并证明;
(2)如图2,当点E在线段BC的延长线上,且∠EAF=45°时,试探究BE,EF,DF之间的数量关系,并说明理由.
19.在△ABC中,点O是AC边上一动点,点P在BC延长线上,过点O的直线DE∥BC交∠ACB与∠ACP的平分线于点D、E.
(1)点O在什么位置时,四边形ADCE是矩形?说明理由.
(2)在(1)的条件下,当AC与BC满足什么条件时,四边形ADCE是正方形?为什么?
20.已知:如图,在△ABC中,∠A>90°.以AB、AC为边分别在△ABC形外作正方形ABDE和正方形ACFG,EB、BC、CG、GE的中点分别是P、Q、M、N.
(1)若连接BG、CE,求证:BG=CE.
(2)试判断四边形PQMN为怎样的四边形,并证明你的结论.
21.如图,四边形ABCD是正方形,点E,K分别在BC,AB上,点G在BA的延长线上,且CE=BK=AG.
(1)判断CK与GD的位置关系为 ,判断四边形GKCD的形状为 ;
(2)求证:DE=DG;
(3)求证:DE⊥CK.
22.已知:如图,△ABC中,M是BA延长线上一点,AF平分∠MAC,AD是△ABC的中线,E是AC的中点,过点A作AF∥BC,与DE的延长线相交于点F.
(1)求证:四边形ADCF是矩形.
(2)当△ABC还满足一个什么条件时,四边形ADCF是正方形?请说明理由.
参考答案
一.选择题(共12小题)
1--10CDBAD DCCDD 11--12BD
二.填空题(共5小题)
13.64
14.8﹣8或8+8
15.AB=BC
16.39
17.
三.解答题(共5小题)
18.解:(1)EF=BE+DF.理由如下:
如图1,
∵四边形ABCD为正方形,
∴AD=AB,∠ABG=∠ADF=90°,
在△ADF和△ABG中,
,
∴△ADF≌△ABG(SAS),
∴AF=AG,∠DAF=∠BAG,
∵四边形ABCD为正方形,
∴∠BAD=90°,
∵∠EAF=45°,
∴∠BAE+∠DAF=45°,
∴∠BAG+∠BAE=45°=∠EAF,
∴∠GAE=∠EAF=45°,
在△AGE和△AFE中,
,
∴△AGE≌△AFE(SAS),
∴GE=EF,
∵GE=GB+BE=BE+DF,
∴EF=BE+DF.
故答案为:EF=BE+DF;
(2)EF=BE﹣DF,理由如下:
如图2,在BC上截取BG=DF,连接AG.
∵四边形ABCD为正方形,
∴AD=AB,∠ABG=∠ADF=90°,
∵BG=DF,
在△ADF和△ABG中,
,
∴△ADF≌△ABG(SAS),
∴AF=AG,∠DAF=∠BAG,
∵四边形ABCD为正方形,
∴∠BAD=90°,
∵∠EAF=45°,
∴∠DAE+∠DAF=45°,
∴∠DAE+∠BAG=45°,
∴∠GAE=∠EAF=45°,
在△AGE和△AFE中,
,
∴△AGE≌△AFE(SAS),
∴GE=EF,
∵GE=BE﹣BG=BE﹣DF,
∴EF=BE﹣DF.
19.解:(1)当O为AC的中点则四边形ADCE是矩形;
理由:∵CE平分∠ACP,
∴∠ACE=∠PCE,
∵DE∥BC,
∴∠OEC=∠ECP,
∴∠OEC=∠OCE,
∴OE=OC,
同理,OC=OD,
∴OD=OE.
∵AO=CO,EO=DO,
∴四边形ADCE为平行四边形,
∵DC、CE是∠ACB与∠ACP的平分线,
∴∠DCE=90°,
∴四边形AECF是矩形;
(2)当AC⊥BC时,四边形ADCE是正方形.
理由:∵∠BCA=90°,
∵DE∥CB,
∴∠DOA=90°,
则DE⊥AC,
∴矩形AECF是正方形.
20.(1)证明:连接BG和CE交于O,
∵四边形ABDE和四边形ACFG是正方形,
∴AB=AE,AC=AG,∠EAB=∠GAC,
∴∠EAB+∠EAG=∠GAC+∠EAG,
∴∠GAB=∠EAC,
在△BAG和△EAC中,
,
∴△BAG≌△EAC(SAS),
∴BG=CE.
(2)四边形PQMN为正方形,
证明:∵EB、BC、CG、GE的中点分别是P、Q、M、N,
∴PN∥BG,MN=CE,MN∥CE,PQ=CE,PQ∥CE,PN=BG,
∵BG=CE,
∴PN=MN,MN=PQ,MN∥PQ,
∴四边形PQMN是菱形,
∵△BAG≌△EAC,
∴∠GBA=∠AEC,
∵四边形ABDE是正方形,
∴∠EAB=90°,
∴∠ABG+∠BWA=90°,
∵∠BWA=∠GWE,
∴∠GWE+∠AEC=90°,
∴∠EOW=180°﹣90°=90°,
∵MN∥CE,PN∥BG,
∴∠NZO=∠EOW=90°,∠NIO=90°,
∴∠MNP=360°﹣90°﹣90°﹣90°=90°
∴菱形PQMN是正方形,
即四边形PQMN为正方形.
21.(1)解:CK与GD的位置关系为CK∥GD,四边形GKCD的形状为平行四边形,
理由:∵四边形ABCD是正方形,
∴∠B=∠BAD=90°,AD=BC,
∴∠GAD=∠B=90°,
在△ADG与△BCK中,
,
∴△ADG≌△BCK(SAS),
∴∠G=∠BKC,
∴CK∥DG,
∵KG∥CD,
∴四边形GKCD为平行四边形;
故答案为:CK∥GD,平行四边形;
(2)证明:∵四边形ABCD是正方形,
∴AD=DC,∠GAD=∠DCE=90°,
在△GAD和△ECD中,
,
∴△GAD≌△ECD(SAS),
∴DE=DG;
(3)证明:∵四边形ABCD是正方形,
∴∠ADC=90°,
∵△GAD≌△ECD,
∴∠GDA=∠CDE,
∴∠GDE=∠GDA+∠ADE=∠CDE+∠ADE=∠ADC=90°,
∴DE⊥DG.
22.(1)证明:∵AD是△ABC的中线,E是AC的中点,
∴DE是△ABC的中位线,
∴DE∥AB,
∵AF∥BC,
∴四边形ABDF是平行四边形,
∴AF=BD.
∵AD是△ABC的中线,
∴BD=CD,
∴AF=CD.
∵AF∥BC,
∴四边形ADCF是平行四边形.
∵AF平分∠MAC,
∴∠MAF=∠CAF.
∵AF∥BC,
∴∠MAF=∠B,∠CAF=∠ACB,
∴∠B=∠ACB,
∴AB=AC,
∴AD⊥BC,
∴∠ADC=90°,
∴平行四边形ADCF是矩形;
(2)解:△ABC还满足∠BAC=90°时,四边形ADCF是正方形.理由如下:
∵∠BAC=90°,D是BC的中点,
∴AD=BC=CD,
∵平行四边形ADCF是矩形;
∴四边形ADCF是正方形
一.选择题(共12小题)
1.下列说法中,正确的是( )
A.一组对边平行的四边形是平行四边形
B.有一个角是直角的四边形是矩形
C.四条边相等的四边形是菱形
D.对角线互相垂直平分的四边形是正方形
2.四边形ABCD的对角线AC、BD交于点O,有下列论断:
①AB=BC;②∠DAB=90°;③BO=DO,AO=CO;
④矩形ABCD;⑤菱形ABCD;⑥正方形ABCD.
其中推理不正确的是( )
A. B. C. D.
3.已知四边形ABCD是平行四边形,再从①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD四个条件中,选两个作为补充条件后,使得四边形ABCD是正方形,现有下列四种选法,其中不正确的是( )
A.①② B.②③ C.①③ D.②④
4.下列是关于某个四边形的三个结论:①它的对角线互相垂直;②它是一个正方形;③它是一个菱形.下列推理过程正确的是( )
A.由②推出③,由③推出① B.由①推出②,由②推出③
C.由③推出①,由①推出③ D.由①推出③,由③推出②
5.如图,在正方形ABCD中,点F为AB上一点,CF与BD交于点E,连接AE,若∠BCF=20°,则∠AEF为( )
A.35° B.40° C.45° D.50°
6.如图,在正方形ABCD内有一点P,PA=AB,PB=PC,若对角线BD与AP交于点M,则∠AMD的度数为( )
A.60° B.65° C.70° D.75°
7.如图,已知正方形ABCD的边长为3,点P是对角线BD上的一点,PF⊥AD于点F,PE⊥AB于点E,连接PC,当PE:PF=1:2时,则PC=( )
A. B.2 C. D.
8.如图,在四边形ABCD中,AB=AD,BC=DC,AC,BD交于点O.添加一个条件使这个四边形成为一种特殊的平行四边形,则以下说法中正确的个数是( )
①添加“AB∥CD“,则四边形ABCD是菱形
②添加“∠BAD=90”,则四边形ABCD是矩形
③添加“OA=OC“,则四边形ABCD是菱形
④添加“∠ABC=∠BCD=90°”,则四边形ABCD是正方形
A.1个 B.2个 C.3个 D.4个
9.如图,四边形ABCD的对角线AC、BD相交于O,下列判断正确的是( )
A.若AC⊥BD,则四边形ABCD是菱形
B.若AC=BD,则四边形ABCD是矩形
C.若AC⊥BD,AC=BD,则四边形ABCD是正方形
D.若AO=OC,BO=OD,则四边形ABCD是平行四边形
10.如图,四边形ABCD是平行四边形,下列结论中错误的是( )
A.当 ABCD是矩形时,∠ABC=90°
B.当 ABCD是菱形时,AC⊥BD
C.当 ABCD是正方形时,AC=BD
D.当 ABCD是菱形时,AB=AC
11.将图1中两个三角形按图2所示的方式摆放,其中四边形ABCD为矩形,连接PQ,MN,甲、乙两人有如下结论:
甲:若四边形ABCD为正方形,则四边形PQMN必是正方形;
乙:若四边形PQMN为正方形,则四边形ABCD必是正方形.
下列判断正确的是( )
A.甲正确,乙不正确 B.甲不正确,乙正确
C.甲、乙都不正确 D.甲、乙都正确
12.如图,在△ABC中,∠BAC=45°,AD⊥BC于点D.点E,F是AD上两点,且DE=DB,DF=DC,若BD=2,CD=3.则的值为( )
A. B. C. D.
二.填空题(共5小题)
13.如图,在正方形ABCD中,E是AB的中点,点G,H分别在AD,BC上,且GH⊥EC.若DG=2,CH=6,则正方形ABCD的面积是 .
14.如图,在正方形ABCD中,AB=6,点E是边AB上的点,且,点F是对角线BD所在直线上一点且BF=BE.过点F作∠EFG=90°,边FG交直线AD于点G,则AG的长为 .
15.在矩形ABCD中,再增加条件 (只需填一个)可使矩形ABCD成为正方形.
16.如图,在四边形ABCD中,∠BAD=45°,∠BCD=90°,连接BD、CA,且CA平分∠BCD,若AC=45,BC=15,则BD= .
17.如图,在正方形ABCD的右下角有一个正方形GICJ,以点G为顶点向左构造正方形EFGH,使点E,F分别落在边AB,BI上,当A,H,J三点共线时,则的值是 .
三.解答题(共5小题)
18.(1)我们知道,正方形的四条边都相等,四个角都为直角.如图1,在正方形ABCD中,点E,F分别在边BC,CD上,连接AE,AF,EF,并延长CB到点G,使BG=DF,连接AG.若∠EAF=45°,猜想BE,EF,DF之间的数量关系并证明;
(2)如图2,当点E在线段BC的延长线上,且∠EAF=45°时,试探究BE,EF,DF之间的数量关系,并说明理由.
19.在△ABC中,点O是AC边上一动点,点P在BC延长线上,过点O的直线DE∥BC交∠ACB与∠ACP的平分线于点D、E.
(1)点O在什么位置时,四边形ADCE是矩形?说明理由.
(2)在(1)的条件下,当AC与BC满足什么条件时,四边形ADCE是正方形?为什么?
20.已知:如图,在△ABC中,∠A>90°.以AB、AC为边分别在△ABC形外作正方形ABDE和正方形ACFG,EB、BC、CG、GE的中点分别是P、Q、M、N.
(1)若连接BG、CE,求证:BG=CE.
(2)试判断四边形PQMN为怎样的四边形,并证明你的结论.
21.如图,四边形ABCD是正方形,点E,K分别在BC,AB上,点G在BA的延长线上,且CE=BK=AG.
(1)判断CK与GD的位置关系为 ,判断四边形GKCD的形状为 ;
(2)求证:DE=DG;
(3)求证:DE⊥CK.
22.已知:如图,△ABC中,M是BA延长线上一点,AF平分∠MAC,AD是△ABC的中线,E是AC的中点,过点A作AF∥BC,与DE的延长线相交于点F.
(1)求证:四边形ADCF是矩形.
(2)当△ABC还满足一个什么条件时,四边形ADCF是正方形?请说明理由.
参考答案
一.选择题(共12小题)
1--10CDBAD DCCDD 11--12BD
二.填空题(共5小题)
13.64
14.8﹣8或8+8
15.AB=BC
16.39
17.
三.解答题(共5小题)
18.解:(1)EF=BE+DF.理由如下:
如图1,
∵四边形ABCD为正方形,
∴AD=AB,∠ABG=∠ADF=90°,
在△ADF和△ABG中,
,
∴△ADF≌△ABG(SAS),
∴AF=AG,∠DAF=∠BAG,
∵四边形ABCD为正方形,
∴∠BAD=90°,
∵∠EAF=45°,
∴∠BAE+∠DAF=45°,
∴∠BAG+∠BAE=45°=∠EAF,
∴∠GAE=∠EAF=45°,
在△AGE和△AFE中,
,
∴△AGE≌△AFE(SAS),
∴GE=EF,
∵GE=GB+BE=BE+DF,
∴EF=BE+DF.
故答案为:EF=BE+DF;
(2)EF=BE﹣DF,理由如下:
如图2,在BC上截取BG=DF,连接AG.
∵四边形ABCD为正方形,
∴AD=AB,∠ABG=∠ADF=90°,
∵BG=DF,
在△ADF和△ABG中,
,
∴△ADF≌△ABG(SAS),
∴AF=AG,∠DAF=∠BAG,
∵四边形ABCD为正方形,
∴∠BAD=90°,
∵∠EAF=45°,
∴∠DAE+∠DAF=45°,
∴∠DAE+∠BAG=45°,
∴∠GAE=∠EAF=45°,
在△AGE和△AFE中,
,
∴△AGE≌△AFE(SAS),
∴GE=EF,
∵GE=BE﹣BG=BE﹣DF,
∴EF=BE﹣DF.
19.解:(1)当O为AC的中点则四边形ADCE是矩形;
理由:∵CE平分∠ACP,
∴∠ACE=∠PCE,
∵DE∥BC,
∴∠OEC=∠ECP,
∴∠OEC=∠OCE,
∴OE=OC,
同理,OC=OD,
∴OD=OE.
∵AO=CO,EO=DO,
∴四边形ADCE为平行四边形,
∵DC、CE是∠ACB与∠ACP的平分线,
∴∠DCE=90°,
∴四边形AECF是矩形;
(2)当AC⊥BC时,四边形ADCE是正方形.
理由:∵∠BCA=90°,
∵DE∥CB,
∴∠DOA=90°,
则DE⊥AC,
∴矩形AECF是正方形.
20.(1)证明:连接BG和CE交于O,
∵四边形ABDE和四边形ACFG是正方形,
∴AB=AE,AC=AG,∠EAB=∠GAC,
∴∠EAB+∠EAG=∠GAC+∠EAG,
∴∠GAB=∠EAC,
在△BAG和△EAC中,
,
∴△BAG≌△EAC(SAS),
∴BG=CE.
(2)四边形PQMN为正方形,
证明:∵EB、BC、CG、GE的中点分别是P、Q、M、N,
∴PN∥BG,MN=CE,MN∥CE,PQ=CE,PQ∥CE,PN=BG,
∵BG=CE,
∴PN=MN,MN=PQ,MN∥PQ,
∴四边形PQMN是菱形,
∵△BAG≌△EAC,
∴∠GBA=∠AEC,
∵四边形ABDE是正方形,
∴∠EAB=90°,
∴∠ABG+∠BWA=90°,
∵∠BWA=∠GWE,
∴∠GWE+∠AEC=90°,
∴∠EOW=180°﹣90°=90°,
∵MN∥CE,PN∥BG,
∴∠NZO=∠EOW=90°,∠NIO=90°,
∴∠MNP=360°﹣90°﹣90°﹣90°=90°
∴菱形PQMN是正方形,
即四边形PQMN为正方形.
21.(1)解:CK与GD的位置关系为CK∥GD,四边形GKCD的形状为平行四边形,
理由:∵四边形ABCD是正方形,
∴∠B=∠BAD=90°,AD=BC,
∴∠GAD=∠B=90°,
在△ADG与△BCK中,
,
∴△ADG≌△BCK(SAS),
∴∠G=∠BKC,
∴CK∥DG,
∵KG∥CD,
∴四边形GKCD为平行四边形;
故答案为:CK∥GD,平行四边形;
(2)证明:∵四边形ABCD是正方形,
∴AD=DC,∠GAD=∠DCE=90°,
在△GAD和△ECD中,
,
∴△GAD≌△ECD(SAS),
∴DE=DG;
(3)证明:∵四边形ABCD是正方形,
∴∠ADC=90°,
∵△GAD≌△ECD,
∴∠GDA=∠CDE,
∴∠GDE=∠GDA+∠ADE=∠CDE+∠ADE=∠ADC=90°,
∴DE⊥DG.
22.(1)证明:∵AD是△ABC的中线,E是AC的中点,
∴DE是△ABC的中位线,
∴DE∥AB,
∵AF∥BC,
∴四边形ABDF是平行四边形,
∴AF=BD.
∵AD是△ABC的中线,
∴BD=CD,
∴AF=CD.
∵AF∥BC,
∴四边形ADCF是平行四边形.
∵AF平分∠MAC,
∴∠MAF=∠CAF.
∵AF∥BC,
∴∠MAF=∠B,∠CAF=∠ACB,
∴∠B=∠ACB,
∴AB=AC,
∴AD⊥BC,
∴∠ADC=90°,
∴平行四边形ADCF是矩形;
(2)解:△ABC还满足∠BAC=90°时,四边形ADCF是正方形.理由如下:
∵∠BAC=90°,D是BC的中点,
∴AD=BC=CD,
∵平行四边形ADCF是矩形;
∴四边形ADCF是正方形
