3.2 圆锥(同步测试)-2023-2024学年六年级下册数学人教版(含答案)
文档属性
| 名称 | 3.2 圆锥(同步测试)-2023-2024学年六年级下册数学人教版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 82.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-22 11:30:08 | ||
图片预览

文档简介
3.2 圆锥(同步测试)-2023-2024学年六年级下册数学人教版
一、单选题
1.一个圆柱和一个圆锥等底等高,它们的体积相差28立方分米,圆锥的体积是( )立方分米。
A.14 B.28 C.42 D.84
2.一个直角三角形的直角边分别是6厘米、3厘米,绕较长的直角边旋转一周,得到的立体图形的体积是( )立方厘米。
A.56.52 B.78.5
C.113.04 D.56.52或113.04
3.如图的圆柱杯子与圆锥杯子底面积相等,把圆锥装满水倒进圆柱里,至少要( )杯才能把圆柱装满。
A.3 B.6 C.9 D.12
4.一个圆柱和一个圆锥高的比是1:4,底面积的比是2:1,体积的比是( )。
A.2:1 B.4:3 C.3:2 D.2:3
5.一个圆锥的高不变,底面半径扩大2倍,它的体积扩大( )
A.2倍 B.3倍 C.4倍 D.8倍
二、判断题
6.圆锥体积一定是圆柱体积的三分之一。( )
7.圆柱的体积是圆锥的体积的3倍,圆柱和圆锥一定等底等高。( )
8. 、、、中,有3个圆柱和1个圆锥。( )
9.把一个圆柱体的橡皮泥捏成圆锥体后,它的体积减少了 .( )
10.底面周长相等、高也相等的两个圆锥,它们的体积也相等。( )
三、填空题
11.等底等高的圆柱和圆锥的体积相差12 dm3,这个圆柱的体积是 dm3。
12.把一个棱长是4dm的正方体容器装满水后,全部倒入一个底面积是12dm2的圆锥形容器,正好装满,这个圆锥形容器的高是 dm。(容器壁厚度不计)
13.一个圆柱与一个圆锥等底等高,它们的体积之差是36立方分米。则圆锥和圆柱的体积之和是 立方分米。
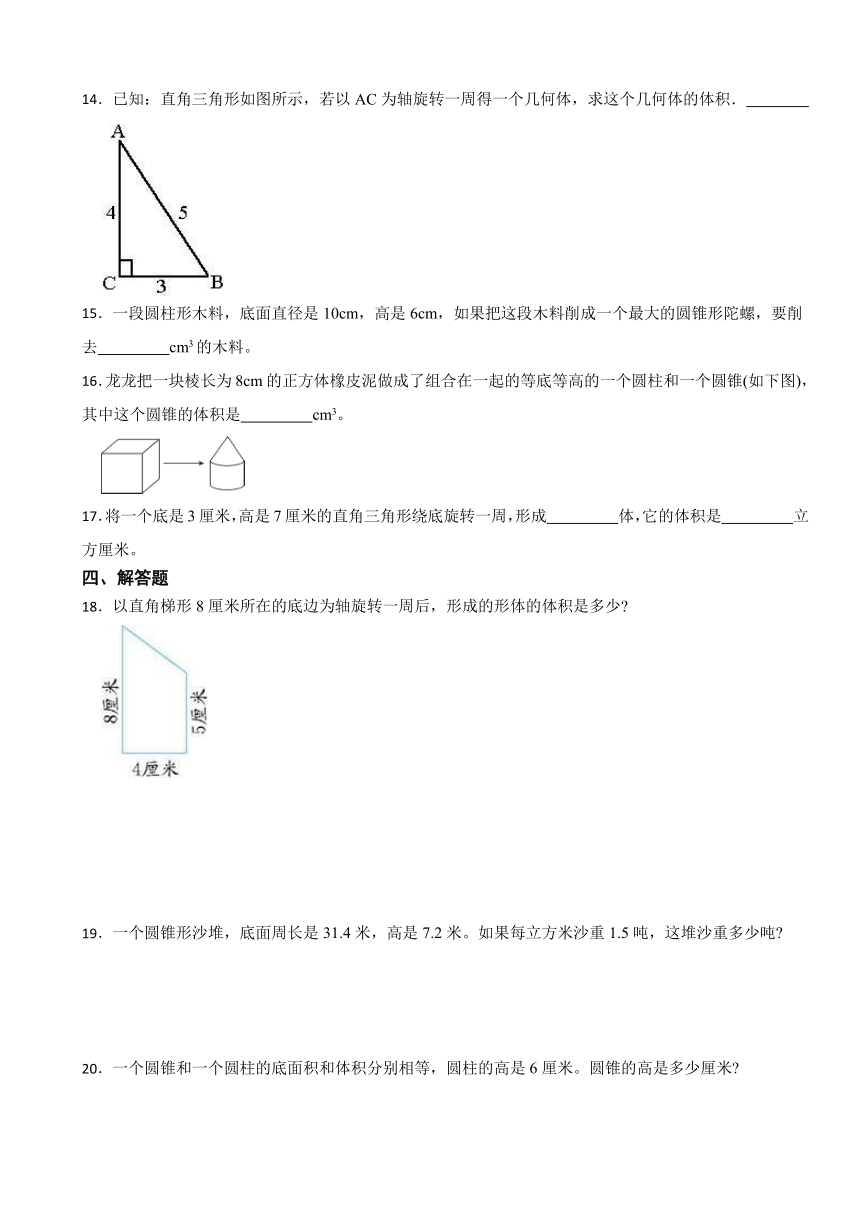
14.已知:直角三角形如图所示,若以AC为轴旋转一周得一个几何体,求这个几何体的体积.
15.一段圆柱形木料,底面直径是10cm,高是6cm,如果把这段木料削成一个最大的圆锥形陀螺,要削去 cm3的木料。
16.龙龙把一块棱长为8cm的正方体橡皮泥做成了组合在一起的等底等高的一个圆柱和一个圆锥(如下图),其中这个圆锥的体积是 cm3。
17.将一个底是3厘米,高是7厘米的直角三角形绕底旋转一周,形成 体,它的体积是 立方厘米。
四、解答题
18.以直角梯形8厘米所在的底边为轴旋转一周后,形成的形体的体积是多少
19.一个圆锥形沙堆,底面周长是31.4米,高是7.2米。如果每立方米沙重1.5吨,这堆沙重多少吨
20.一个圆锥和一个圆柱的底面积和体积分别相等,圆柱的高是6厘米。圆锥的高是多少厘米
21.把一块棱长为10cm的正方体铁块熔铸成一个底面直径是20cm的圆锥形铁块。这个圆锥形铁块的高约是多少?(得数保留整cm)
22.一堆煤成圆锥形,高1.8m,底面周长为31.4m。已知每立方米的煤约重1.4t,这堆煤大约重多少吨?(得数保留整数。)
23.一个圆锥形谷堆,高1米,底面周长是18.84米,每立方米稻谷重1.2吨。
(1)它的占地面积是多少平方米?
(2)这堆稻谷重多少吨?
24.一个圆锥形容器里装有水0.5升,水面高度正好是圆锥高度的一半,这个容器还能装水多少升?
答案解析部分
1.【答案】A
2.【答案】A
3.【答案】C
4.【答案】C
5.【答案】C
6.【答案】错误
7.【答案】错误
8.【答案】错误
9.【答案】错误
10.【答案】正确
11.【答案】18
12.【答案】16
13.【答案】72
14.【答案】12π
15.【答案】314
16.【答案】128
17.【答案】圆锥;65.94
18.【答案】解:42×3.14×8=401.92(立方厘米)
42×3.14×(8-5)×=50.24(立方厘米)
401.92-50.24=351.68(立方厘米)
答:形成的形体的体积是351.68立方厘米。
19.【答案】解:3.14×(31.4÷3.14÷2)2×7.2× ×1.5
=3.14×25×2.4×1.5
=3.14×90
=282.6(吨)
答:这堆沙重282.6吨.
20.【答案】解:6÷ =18(厘米)
答:圆锥的高是18厘米.
21.【答案】解:20÷2=10(cm)
10×10×10×3÷(3.14×102)
=3000÷314
≈10(cm)
答:这个圆锥形铁块的高约10cm。
22.【答案】解:(31.4÷3.14÷2)2×3.14×1.8× ×1.4=65.94(吨)≈66(吨)
答:这堆煤大约重66吨。
23.【答案】(1)解:底面半径:18.84÷3.14÷2=3(米)
占地面积:3.14×32=254.34(平方米)
答:它的占地面积是254.34平方米。
(2)解:254.34×1××1.2
=84.78×1.2
=11.304(吨)
答:这堆稻谷重11.304吨。
24.【答案】0.5×(8-1)=3.5(升)
答:还能装水3.5升。
一、单选题
1.一个圆柱和一个圆锥等底等高,它们的体积相差28立方分米,圆锥的体积是( )立方分米。
A.14 B.28 C.42 D.84
2.一个直角三角形的直角边分别是6厘米、3厘米,绕较长的直角边旋转一周,得到的立体图形的体积是( )立方厘米。
A.56.52 B.78.5
C.113.04 D.56.52或113.04
3.如图的圆柱杯子与圆锥杯子底面积相等,把圆锥装满水倒进圆柱里,至少要( )杯才能把圆柱装满。
A.3 B.6 C.9 D.12
4.一个圆柱和一个圆锥高的比是1:4,底面积的比是2:1,体积的比是( )。
A.2:1 B.4:3 C.3:2 D.2:3
5.一个圆锥的高不变,底面半径扩大2倍,它的体积扩大( )
A.2倍 B.3倍 C.4倍 D.8倍
二、判断题
6.圆锥体积一定是圆柱体积的三分之一。( )
7.圆柱的体积是圆锥的体积的3倍,圆柱和圆锥一定等底等高。( )
8. 、、、中,有3个圆柱和1个圆锥。( )
9.把一个圆柱体的橡皮泥捏成圆锥体后,它的体积减少了 .( )
10.底面周长相等、高也相等的两个圆锥,它们的体积也相等。( )
三、填空题
11.等底等高的圆柱和圆锥的体积相差12 dm3,这个圆柱的体积是 dm3。
12.把一个棱长是4dm的正方体容器装满水后,全部倒入一个底面积是12dm2的圆锥形容器,正好装满,这个圆锥形容器的高是 dm。(容器壁厚度不计)
13.一个圆柱与一个圆锥等底等高,它们的体积之差是36立方分米。则圆锥和圆柱的体积之和是 立方分米。
14.已知:直角三角形如图所示,若以AC为轴旋转一周得一个几何体,求这个几何体的体积.
15.一段圆柱形木料,底面直径是10cm,高是6cm,如果把这段木料削成一个最大的圆锥形陀螺,要削去 cm3的木料。
16.龙龙把一块棱长为8cm的正方体橡皮泥做成了组合在一起的等底等高的一个圆柱和一个圆锥(如下图),其中这个圆锥的体积是 cm3。
17.将一个底是3厘米,高是7厘米的直角三角形绕底旋转一周,形成 体,它的体积是 立方厘米。
四、解答题
18.以直角梯形8厘米所在的底边为轴旋转一周后,形成的形体的体积是多少
19.一个圆锥形沙堆,底面周长是31.4米,高是7.2米。如果每立方米沙重1.5吨,这堆沙重多少吨
20.一个圆锥和一个圆柱的底面积和体积分别相等,圆柱的高是6厘米。圆锥的高是多少厘米
21.把一块棱长为10cm的正方体铁块熔铸成一个底面直径是20cm的圆锥形铁块。这个圆锥形铁块的高约是多少?(得数保留整cm)
22.一堆煤成圆锥形,高1.8m,底面周长为31.4m。已知每立方米的煤约重1.4t,这堆煤大约重多少吨?(得数保留整数。)
23.一个圆锥形谷堆,高1米,底面周长是18.84米,每立方米稻谷重1.2吨。
(1)它的占地面积是多少平方米?
(2)这堆稻谷重多少吨?
24.一个圆锥形容器里装有水0.5升,水面高度正好是圆锥高度的一半,这个容器还能装水多少升?
答案解析部分
1.【答案】A
2.【答案】A
3.【答案】C
4.【答案】C
5.【答案】C
6.【答案】错误
7.【答案】错误
8.【答案】错误
9.【答案】错误
10.【答案】正确
11.【答案】18
12.【答案】16
13.【答案】72
14.【答案】12π
15.【答案】314
16.【答案】128
17.【答案】圆锥;65.94
18.【答案】解:42×3.14×8=401.92(立方厘米)
42×3.14×(8-5)×=50.24(立方厘米)
401.92-50.24=351.68(立方厘米)
答:形成的形体的体积是351.68立方厘米。
19.【答案】解:3.14×(31.4÷3.14÷2)2×7.2× ×1.5
=3.14×25×2.4×1.5
=3.14×90
=282.6(吨)
答:这堆沙重282.6吨.
20.【答案】解:6÷ =18(厘米)
答:圆锥的高是18厘米.
21.【答案】解:20÷2=10(cm)
10×10×10×3÷(3.14×102)
=3000÷314
≈10(cm)
答:这个圆锥形铁块的高约10cm。
22.【答案】解:(31.4÷3.14÷2)2×3.14×1.8× ×1.4=65.94(吨)≈66(吨)
答:这堆煤大约重66吨。
23.【答案】(1)解:底面半径:18.84÷3.14÷2=3(米)
占地面积:3.14×32=254.34(平方米)
答:它的占地面积是254.34平方米。
(2)解:254.34×1××1.2
=84.78×1.2
=11.304(吨)
答:这堆稻谷重11.304吨。
24.【答案】0.5×(8-1)=3.5(升)
答:还能装水3.5升。
