3.5《长方体和正方体的体积》(教案)-2023-2024学年五年级下册数学人教版(表格式)
文档属性
| 名称 | 3.5《长方体和正方体的体积》(教案)-2023-2024学年五年级下册数学人教版(表格式) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-22 13:20:48 | ||
图片预览


文档简介
人教版数学五年级下册
三《长方体和正方体的体积》
教学设计
课题 三《长方体和正方体的体积》
教学目标 知识目标:使学生理解并掌握长方体和正方体体积的计算公式,能运用长方体和正方体体积公式解决简单的实际问题。 能力目标:经历长方体和正方体统一体积计算公式的推导过程,进一步认识它们的特征以及它们之间的联系。 情感目标: 通过推导长方体和正方体统一的体积计算公式,加强代数思想的渗透,培养学生类推、迁移的能力。渗透知识来源于实践并应用于实践的辩证唯物主义观点,激发学生的参与意识,营造学生主动学习的良好氛围。
教学重点 理解并掌握长方体和正方体的体积计算方法,长方体和正方体体积公式的统一。
教学难点 理解长方体体积计算公式的推导过程,长方体和正方体统一体积计算公式的推导。
教学准备 教师准备:多媒体课件,长方体、正方体模型 学生准备:课本
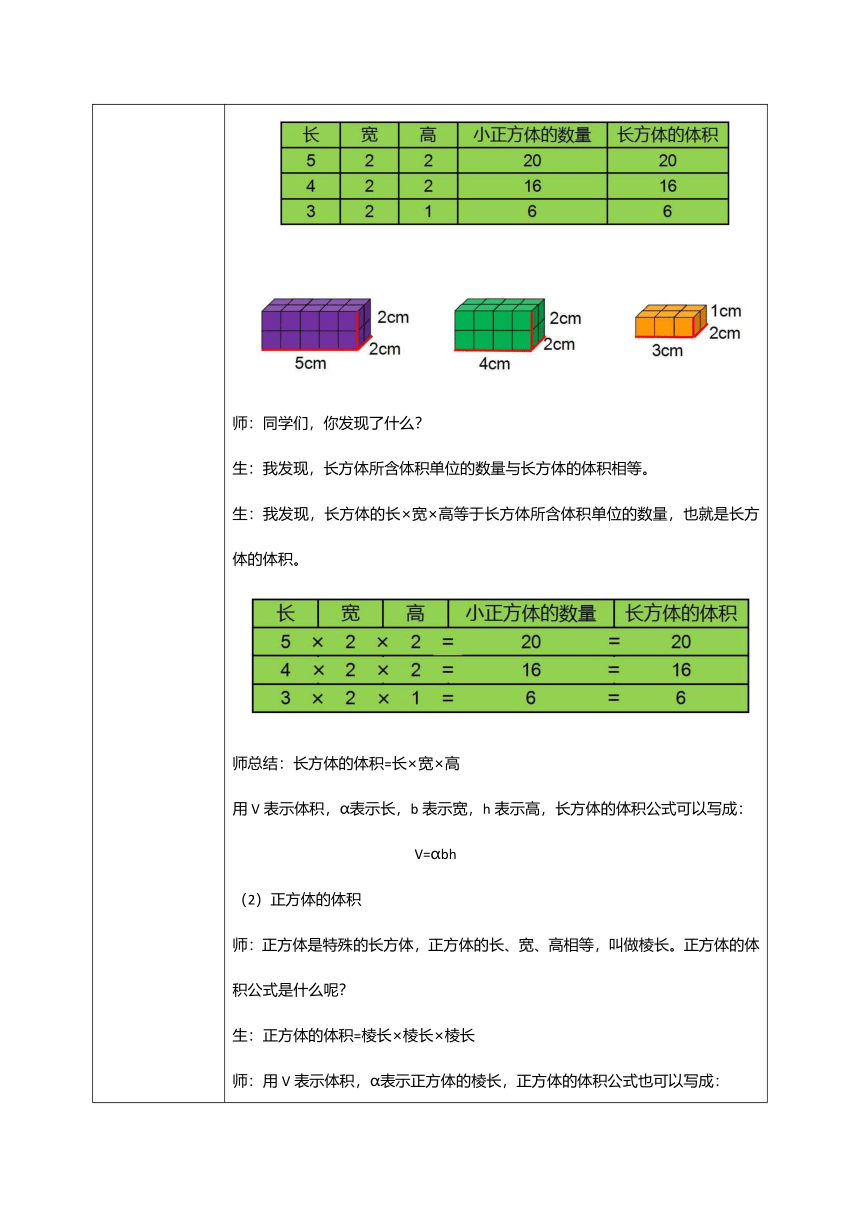
教学过程 新课导入: 复习旧知 填空 ①物体所占空间的大小叫做物体的( )。 ② 计量体积要用体积单位,常用的体积单位有( )、( )和( ),可以分别写成( )、( )和( ) 。 (2)填上合适的单位名称 一块橡皮的体积约是8( ) 运货集装箱的体积约是40( ) 一台录音机的体积约是6( ) 一张写字台大约占地1.5( ) 新课讲解: 长方体的体积 ①课件出示长方体图片,提问:同学们知道怎样求这个长方体的体积吗? 生:可以把它切成小正方体。 生:或许可以先把它的长、宽、高量一量。 小组合作,用体积是1立方厘米的小正方体拼摆长方体,并分别记录摆出的长方体的长、宽、高。 ②汇报结果 师:同学们,你发现了什么? 生:我发现,长方体所含体积单位的数量与长方体的体积相等。 生:我发现,长方体的长×宽×高等于长方体所含体积单位的数量,也就是长方体的体积。 师总结:长方体的体积=长×宽×高 用V表示体积,ɑ表示长,b表示宽,h表示高,长方体的体积公式可以写成: V=ɑbh 正方体的体积 师:正方体是特殊的长方体,正方体的长、宽、高相等,叫做棱长。正方体的体积公式是什么呢? 生:正方体的体积=棱长×棱长×棱长 师:用V表示体积,ɑ表示正方体的棱长,正方体的体积公式也可以写成: V=ɑ 注意:“ɑ ”读作“ɑ的立方”,表示3个ɑ相乘。 计算下面图形的体积 学生根据公式进行计算。 长方体和正方体体积公式的统一 师:长方体和正方体的体积能不能用一个公式来表示呢? 长方体的体积公式是什么? 生:长方体的体积=长×宽×高 师:长×宽是什么? 生:长×宽是长方体底面的面积。 师:我们把长方体底面的面积叫做底面积。长方体的体积公式还可以怎样写呢? 生:长方体的体积=底面积×高 师:正方体底面的面积与什么有关呢? 生:正方体的底面积=棱长×棱长。 师:那么,正方体的体积还可以怎样写呢? 生:正方体的体积=底面积×棱长。 因为正方体的另一条棱长可以看做是正方体的高,所以: 正方体的体积=底面积×高 师总结:长方体(或正方体)的体积=底面积×高 如果用V表示体积,S表示底面积,h表示高,那么长方体和正方体的体积公式还可以怎样写? 生:V=Sh (设计意图:把学习的主动权交给学生,让学生经历长方体和正方体体积的另一种计算方法以及长方体和正方体的统一体积计算公式的推导过程,让学生在学习中体验到快乐,培养学生的学习兴趣和信心。) 课堂练习: 一块长方体豆腐的尺寸如下图,它的体积是多少? (2)一根长方体木料,长5m,横截面的面积是0.06m 。这根木料的体积是多少 (3)判断 正方体的表面积和体积有可能一样大。( ) 一个长方体,相对的两个面的面积一样大。( ) 两个体积相等的正方体,它们的棱长一定向等。( ) 体积相等的两个正方体,它们的表面积一定相等。( ) (4)选择 一个正方体的棱长扩大为原来的3倍,它的体积扩大为原来的( ) A.3倍 B.9倍 C.27倍 一个长方体的体积是24m ,它的长是6m,宽是2m,高是( )m。 A.4 B.2 C.12 D.6 把一个棱长8cm的正方体切成棱长是4cm的小正方体,可以得到 ( )个小正方体。 A.8 B.2 C.16 D.6 (5)要在平地上挖一个长50米,宽30米,深50厘米的长方体土坑,一共要挖出多少方的土? (6)妈妈送给奶奶一个长方体形状的蛋糕,长2dm,宽2dm,高0.6dm。奶奶把它平均分成4块长方体的小蛋糕,那每人分到多大的一块? 课堂小结: 这节课我们学习了长方体的体积、正方体的体积以及长方体和正方体体积的统一公式。
板书设计 长方体和正方体的体积 长方体的体积=长×宽×高 V=ɑbh 正方体的体积=棱长×棱长×棱长 V=ɑ 长方体(或正方体)的体积=底面积×高 V=Sh
课后作业 教材练习七第9、11题。
三《长方体和正方体的体积》
教学设计
课题 三《长方体和正方体的体积》
教学目标 知识目标:使学生理解并掌握长方体和正方体体积的计算公式,能运用长方体和正方体体积公式解决简单的实际问题。 能力目标:经历长方体和正方体统一体积计算公式的推导过程,进一步认识它们的特征以及它们之间的联系。 情感目标: 通过推导长方体和正方体统一的体积计算公式,加强代数思想的渗透,培养学生类推、迁移的能力。渗透知识来源于实践并应用于实践的辩证唯物主义观点,激发学生的参与意识,营造学生主动学习的良好氛围。
教学重点 理解并掌握长方体和正方体的体积计算方法,长方体和正方体体积公式的统一。
教学难点 理解长方体体积计算公式的推导过程,长方体和正方体统一体积计算公式的推导。
教学准备 教师准备:多媒体课件,长方体、正方体模型 学生准备:课本
教学过程 新课导入: 复习旧知 填空 ①物体所占空间的大小叫做物体的( )。 ② 计量体积要用体积单位,常用的体积单位有( )、( )和( ),可以分别写成( )、( )和( ) 。 (2)填上合适的单位名称 一块橡皮的体积约是8( ) 运货集装箱的体积约是40( ) 一台录音机的体积约是6( ) 一张写字台大约占地1.5( ) 新课讲解: 长方体的体积 ①课件出示长方体图片,提问:同学们知道怎样求这个长方体的体积吗? 生:可以把它切成小正方体。 生:或许可以先把它的长、宽、高量一量。 小组合作,用体积是1立方厘米的小正方体拼摆长方体,并分别记录摆出的长方体的长、宽、高。 ②汇报结果 师:同学们,你发现了什么? 生:我发现,长方体所含体积单位的数量与长方体的体积相等。 生:我发现,长方体的长×宽×高等于长方体所含体积单位的数量,也就是长方体的体积。 师总结:长方体的体积=长×宽×高 用V表示体积,ɑ表示长,b表示宽,h表示高,长方体的体积公式可以写成: V=ɑbh 正方体的体积 师:正方体是特殊的长方体,正方体的长、宽、高相等,叫做棱长。正方体的体积公式是什么呢? 生:正方体的体积=棱长×棱长×棱长 师:用V表示体积,ɑ表示正方体的棱长,正方体的体积公式也可以写成: V=ɑ 注意:“ɑ ”读作“ɑ的立方”,表示3个ɑ相乘。 计算下面图形的体积 学生根据公式进行计算。 长方体和正方体体积公式的统一 师:长方体和正方体的体积能不能用一个公式来表示呢? 长方体的体积公式是什么? 生:长方体的体积=长×宽×高 师:长×宽是什么? 生:长×宽是长方体底面的面积。 师:我们把长方体底面的面积叫做底面积。长方体的体积公式还可以怎样写呢? 生:长方体的体积=底面积×高 师:正方体底面的面积与什么有关呢? 生:正方体的底面积=棱长×棱长。 师:那么,正方体的体积还可以怎样写呢? 生:正方体的体积=底面积×棱长。 因为正方体的另一条棱长可以看做是正方体的高,所以: 正方体的体积=底面积×高 师总结:长方体(或正方体)的体积=底面积×高 如果用V表示体积,S表示底面积,h表示高,那么长方体和正方体的体积公式还可以怎样写? 生:V=Sh (设计意图:把学习的主动权交给学生,让学生经历长方体和正方体体积的另一种计算方法以及长方体和正方体的统一体积计算公式的推导过程,让学生在学习中体验到快乐,培养学生的学习兴趣和信心。) 课堂练习: 一块长方体豆腐的尺寸如下图,它的体积是多少? (2)一根长方体木料,长5m,横截面的面积是0.06m 。这根木料的体积是多少 (3)判断 正方体的表面积和体积有可能一样大。( ) 一个长方体,相对的两个面的面积一样大。( ) 两个体积相等的正方体,它们的棱长一定向等。( ) 体积相等的两个正方体,它们的表面积一定相等。( ) (4)选择 一个正方体的棱长扩大为原来的3倍,它的体积扩大为原来的( ) A.3倍 B.9倍 C.27倍 一个长方体的体积是24m ,它的长是6m,宽是2m,高是( )m。 A.4 B.2 C.12 D.6 把一个棱长8cm的正方体切成棱长是4cm的小正方体,可以得到 ( )个小正方体。 A.8 B.2 C.16 D.6 (5)要在平地上挖一个长50米,宽30米,深50厘米的长方体土坑,一共要挖出多少方的土? (6)妈妈送给奶奶一个长方体形状的蛋糕,长2dm,宽2dm,高0.6dm。奶奶把它平均分成4块长方体的小蛋糕,那每人分到多大的一块? 课堂小结: 这节课我们学习了长方体的体积、正方体的体积以及长方体和正方体体积的统一公式。
板书设计 长方体和正方体的体积 长方体的体积=长×宽×高 V=ɑbh 正方体的体积=棱长×棱长×棱长 V=ɑ 长方体(或正方体)的体积=底面积×高 V=Sh
课后作业 教材练习七第9、11题。
