六年级上册数学北师大版 《 圆的面积(一)》(课件)(共23张PPT)
文档属性
| 名称 | 六年级上册数学北师大版 《 圆的面积(一)》(课件)(共23张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-22 14:27:26 | ||
图片预览


文档简介
(共23张PPT)
圆的面积(一)
——如何得到一个圆的面积呢?
问题
思考
应用
创新
北师大版 六年级上册 第一单元 圆
如果每平方米草坪8元,要铺满这个圆形草坪需要多少元?
这个圆形草坪的占地面积也就是这个圆的面积。
【探究1】
圆所占平面的大小叫作圆的面积。
什么是圆的面积?
【探究2】
回忆一下以前学过的平面图形,它们的面积公式是什么?
分别怎么推导出来的?
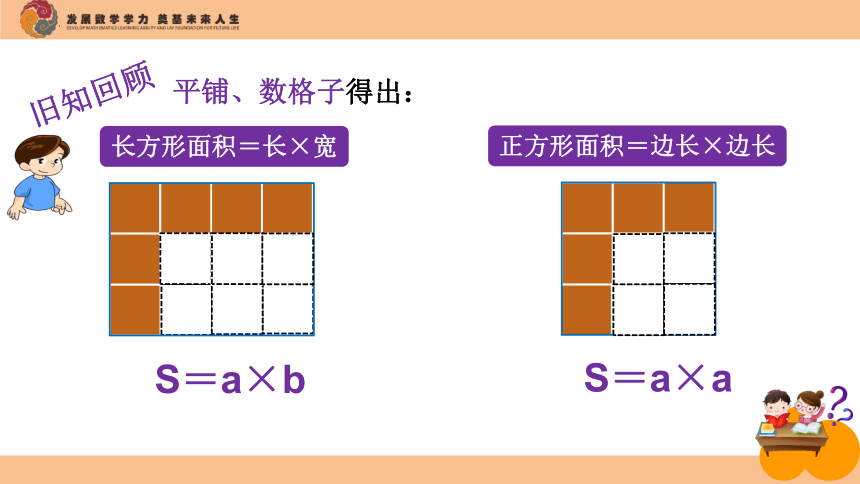
正方形面积=边长×边长
S=a×a
长方形面积=长×宽
S=a×b
旧知回顾
平铺、数格子得出:
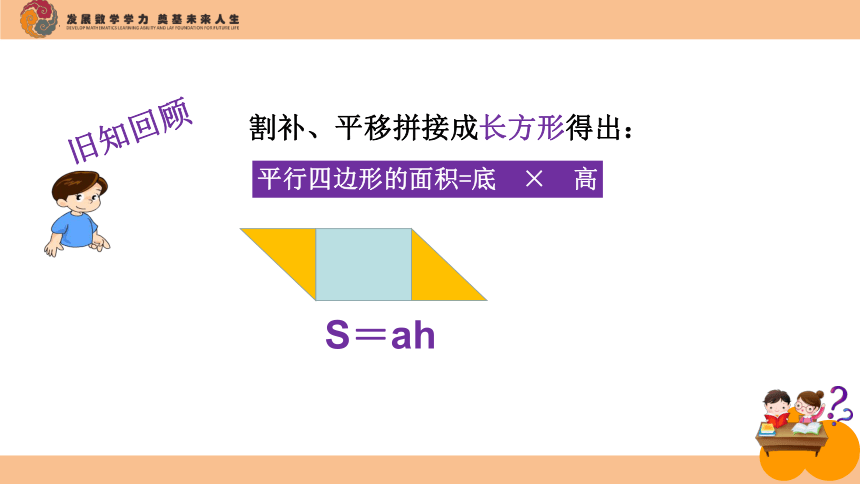
S=ah
平行四边形的面积=底 × 高
割补、平移拼接成长方形得出:
旧知回顾
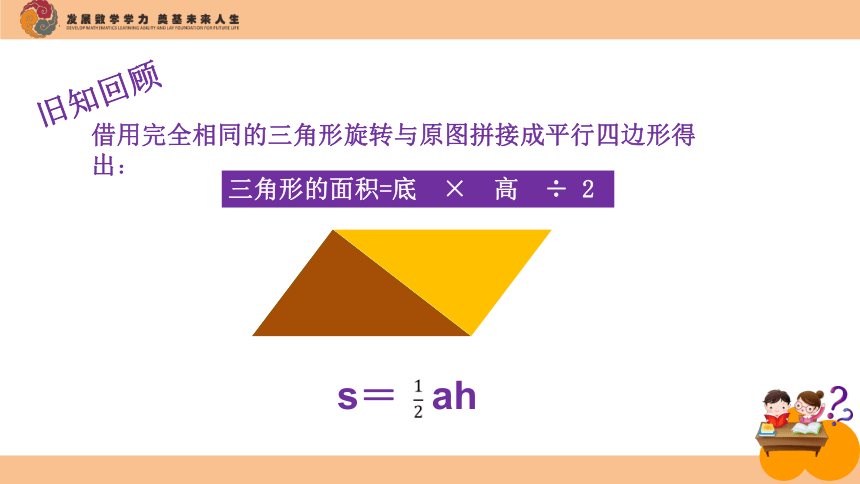
三角形的面积=底 × 高 ÷ 2
借用完全相同的三角形旋转与原图拼接成平行四边形得出:
s= ah
旧知回顾
下底
上底
高
上底
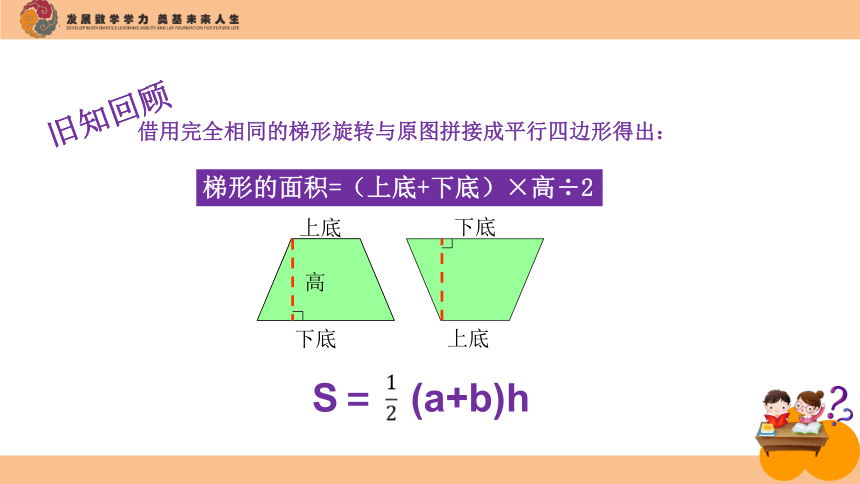
S= (a+b)h
梯形的面积=(上底+下底)×高÷2
旧知回顾
下底
借用完全相同的梯形旋转与原图拼接成平行四边形得出:
以前在探究图形面积计算公式时,通常都是将新的图形( ) 成学过的图形,从而来推导它的面积公式。
【回头看1】
【探究3】
猜一猜:圆的面积的大小和什么有关?
O
圆的面积是r 的2倍多一些。
圆的面积比r 的4倍少一些。
圆的面积与半径的关系究竟是怎样的呢?
r
r
【探究4】
【探究5】
【探究6】
学习要求:
a. 轻轻取出圆形纸片,想一想,折一折;
b. 拿出剪刀沿折痕剪一剪,注意安全;
c. 将剪成的小块拼一拼,看看你有什么发现?
底
高
【探究7】
看一看,想一想,圆等分的份数越多,拼出的图形就越接近什么形状?
C÷2
底
高
圆的面积
圆周长的一半
平行四边形的面积=底 × 高
平行四边形的面积
圆的半径
×
圆的面积=
【探究8】
回顾圆的面积公式的推导过程。
【回头看2】
在探究圆面积的计算方法的活动中,我经历了将圆( )成学过的平面图形的过程,体验到了如果将圆沿( )剪开,一直等分下去,就会将曲线图形圆转化成直线图形( )的数学方法。在整个探究过程中,圆和转化后的平面图形( )变了,( )相等。
圆形草坪的直径是20 m,如果每平方米草皮8元,在这个草坪上铺满草皮,需要多少元?
【巩固应用】
1.课上有同学问我,能不能把剪下来的小扇形拼成三角形或者梯形? 请试着利用拼成的三角形或梯形选择一种推导出圆的面积公式。
一练一总结:推导圆面积公式时,它们的( )变了,( )相等。
三角形(或梯形)的底相当于圆的( ),高相当于圆的( ),三角形(或梯形)的面积=( ),所以圆的面积=( )。
2.
一练一总结:正方形中最大的圆的直径与( )相等,正方形的面积是( ),圆的面积是( ),所以圆的面积是正方形面积的( )倍。
圆的面积(一)
——如何得到一个圆的面积呢?
问题
思考
应用
创新
北师大版 六年级上册 第一单元 圆
如果每平方米草坪8元,要铺满这个圆形草坪需要多少元?
这个圆形草坪的占地面积也就是这个圆的面积。
【探究1】
圆所占平面的大小叫作圆的面积。
什么是圆的面积?
【探究2】
回忆一下以前学过的平面图形,它们的面积公式是什么?
分别怎么推导出来的?
正方形面积=边长×边长
S=a×a
长方形面积=长×宽
S=a×b
旧知回顾
平铺、数格子得出:
S=ah
平行四边形的面积=底 × 高
割补、平移拼接成长方形得出:
旧知回顾
三角形的面积=底 × 高 ÷ 2
借用完全相同的三角形旋转与原图拼接成平行四边形得出:
s= ah
旧知回顾
下底
上底
高
上底
S= (a+b)h
梯形的面积=(上底+下底)×高÷2
旧知回顾
下底
借用完全相同的梯形旋转与原图拼接成平行四边形得出:
以前在探究图形面积计算公式时,通常都是将新的图形( ) 成学过的图形,从而来推导它的面积公式。
【回头看1】
【探究3】
猜一猜:圆的面积的大小和什么有关?
O
圆的面积是r 的2倍多一些。
圆的面积比r 的4倍少一些。
圆的面积与半径的关系究竟是怎样的呢?
r
r
【探究4】
【探究5】
【探究6】
学习要求:
a. 轻轻取出圆形纸片,想一想,折一折;
b. 拿出剪刀沿折痕剪一剪,注意安全;
c. 将剪成的小块拼一拼,看看你有什么发现?
底
高
【探究7】
看一看,想一想,圆等分的份数越多,拼出的图形就越接近什么形状?
C÷2
底
高
圆的面积
圆周长的一半
平行四边形的面积=底 × 高
平行四边形的面积
圆的半径
×
圆的面积=
【探究8】
回顾圆的面积公式的推导过程。
【回头看2】
在探究圆面积的计算方法的活动中,我经历了将圆( )成学过的平面图形的过程,体验到了如果将圆沿( )剪开,一直等分下去,就会将曲线图形圆转化成直线图形( )的数学方法。在整个探究过程中,圆和转化后的平面图形( )变了,( )相等。
圆形草坪的直径是20 m,如果每平方米草皮8元,在这个草坪上铺满草皮,需要多少元?
【巩固应用】
1.课上有同学问我,能不能把剪下来的小扇形拼成三角形或者梯形? 请试着利用拼成的三角形或梯形选择一种推导出圆的面积公式。
一练一总结:推导圆面积公式时,它们的( )变了,( )相等。
三角形(或梯形)的底相当于圆的( ),高相当于圆的( ),三角形(或梯形)的面积=( ),所以圆的面积=( )。
2.
一练一总结:正方形中最大的圆的直径与( )相等,正方形的面积是( ),圆的面积是( ),所以圆的面积是正方形面积的( )倍。
同课章节目录
- 一 圆
- 1 圆的认识(一)
- 2 圆的认识(二)
- 3 欣赏与设计
- 4 圆的周长
- 5 圆的面积(一)
- 6 圆的面积(二)
- 二 分数的混合运算
- 1 分数的混合运算(一)
- 2 分数的混合运算(二)
- 3 分数的混合运算(三)
- 三 观察物体
- 1 搭积木比赛
- 2 观察的范围
- 3 天安门广场
- 四 百分数
- 1 百分数的认识
- 2 合格率
- 3 营养含量
- 4 这月我当家
- 五 数据处理
- 1 扇形统计图
- 2 统计图的选择
- 3 身高的情况
- 4 身高的变化
- 六 比的认识
- 1 生活中的比
- 2 比的化简
- 3 比的应用
- 数学好玩
- 1 反弹高度
- 2 看图找关系
- 3 比赛场次
- 七 百分数的应用
- 1 百分数的应用(一)
- 2 百分数的应用(二)
- 3 百分数的应用(三)
- 4 百分数的应用(四)
