2024年江苏省扬州市高邮市城北中学中考模拟预测数学试题(含答案)
文档属性
| 名称 | 2024年江苏省扬州市高邮市城北中学中考模拟预测数学试题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 919.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-22 15:44:48 | ||
图片预览



文档简介
九年级数学练习
一、选择题(本大题共8小题,每小题3分,共24分)
1.下列图案中是中心对称图形但不是轴对称图形的是( )
A. B. C. D.
2.若,则下列等式成立的是( )
A. B. C. D.
3.空气的成分(除去水汽、杂质等)是:氮气约占,氧气约占,其他微量气体约占.要反映上述信息,宜采用的统计图是( )
A.条形统计图 B.扇形统计图 C.折线统计图 D.频数分布直方图
4.已知的半径是6,点是平面内一点且,则点与的位置关系是( )
A.圆内 B.圆外 C.圆上 D.无法确定
5.在中,的值为( )
A. B. C. D.2
6.如图,是半径为2的上的三点,,则弦的长为( )
A.2 B.4 C. D.
7.根据下表可知,方程的一个解的范围为( )
…… 0.28 0.29 0.30 0.31 0.32 ……
…… 0.0261 0.0624 ……
A. B. C. D.
8.小明同学利用计算机软件绘制函数(为常数)的图象如图所示,由学习函数的经验,可以推断常数的值满足( )
A. B. C. D.
二、填空题(本大题共10小题,每小题3分,共30分)
9.2021年12月28日,连淮扬镇高铁正式运营,在比例尺为的工程示意图上,高邮站到扬州东站全长约为,它的实际长度约为________.
10.在中,若,则________.
11.某种绿豆在相同条件下发芽试验的结果如下:
每批粒数 50 100 500 1000 1500 2000 3000
发芽的频数 44 92 463 928 1396 1866 2794
发芽的频率 0.880 0.920 0.926 0.928 0.931 0.933 0.931
这种绿豆发芽的概率的估计值为________(精确到0.01).
12.如图,小明用图中的扇形纸片作一个圆锥的侧面,已知扇形的圆心角为,半径是,那么这个圆锥的底面半径是________.
13.若是关的方程的解,则的值为________.
14.点在抛物线上,则的大小关系是________(用“<”连接).
15.如图,是的直径,点在的延长线上,切于点,若,则的度数为________.
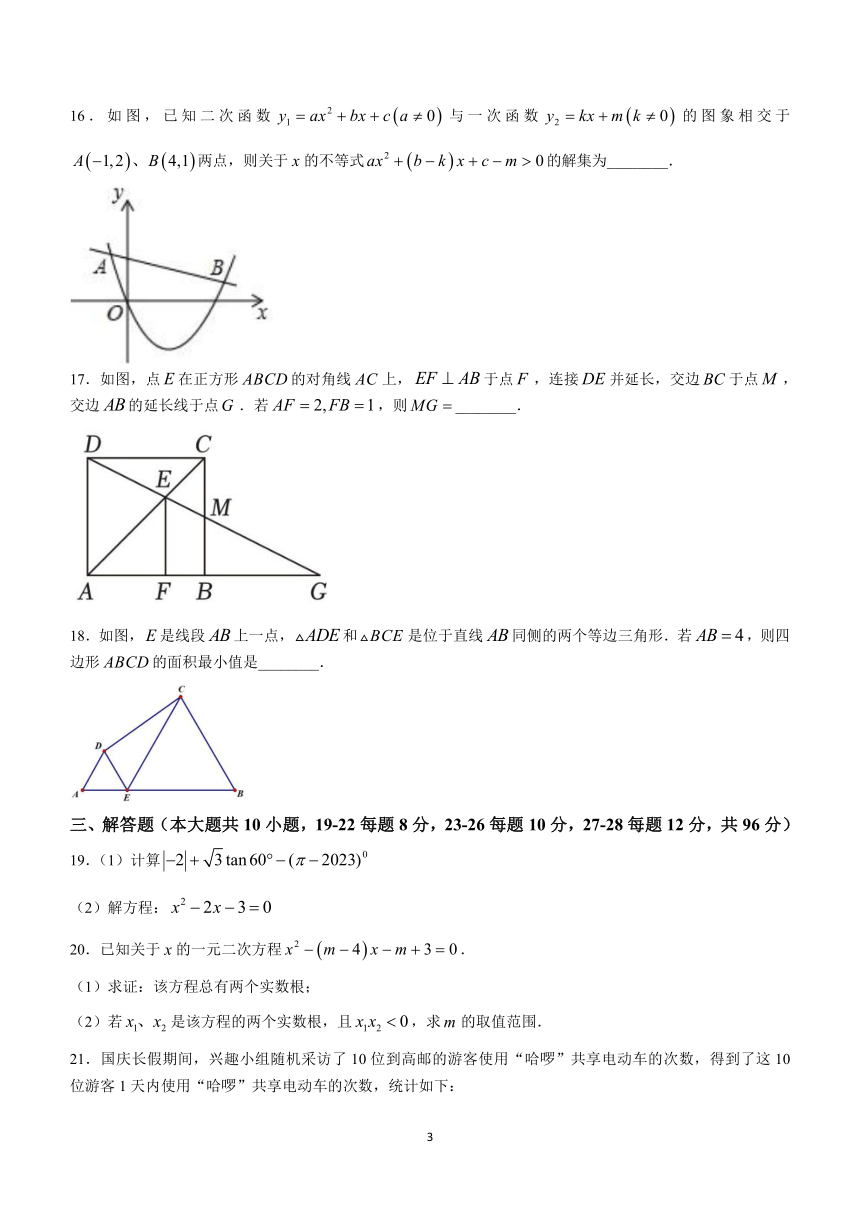
16.如图,已知二次函数与一次函数的图象相交于两点,则关于的不等式的解集为________.
17.如图,点在正方形的对角线上,于点,连接并延长,交边于点,交边的延长线于点.若,则________.
18.如图,是线段上一点,和是位于直线同侧的两个等边三角形.若,则四边形的面积最小值是________.
三、解答题(本大题共10小题,19-22每题8分,23-26每题10分,27-28每题12分,共96分)
19.(1)计算
(2)解方程:
20.已知关于的一元二次方程.
(1)求证:该方程总有两个实数根;
(2)若是该方程的两个实数根,且,求的取值范围.
21.国庆长假期间,兴趣小组随机采访了10位到高邮的游客使用“哈啰”共享电动车的次数,得到了这10位游客1天内使用“哈啰”共享电动车的次数,统计如下:
使用次数 0 2 3 4 6
人数 2 4 1 2 1
(1)这10位游客1天内使用“哈啰”共享电动车的次数的中位数是________次,众数是________次,平均数是________次;
(2)若小明同学把统计表中的数据“6”错看成了“5”,则用“街兔”共享电动车的次数的中位数、众数和平均数这三个统计量中受影响的是________;(填“中位数”、“众数”或“平均数”)
(3)若国庆长假期间,每天约有1200位游客到高邮,试估计这些游客国庆长假期间每天使用“哈啰”共享电动车的总次数.
22.为了深入推动大众旅游,满足人民群众美好生活需要,我市举办中国旅游日惠民周活动,活动主办方在活动现场提供免费门票抽奖箱,里面放有4张相同的卡片,分别写有景区:A.文游台,B.盂城驿,C.高邮当铺,D.龙虬庄遗址.抽奖规则如下:搅匀后从抽奖箱中任意抽取一张卡片,记录后放回,根据抽奖的结果获得相应的景区免费门票.
(1)小明获得一次抽奖机会,他恰好抽到景区A门票的概率是________.
(2)小亮获得两次抽奖机会,用树状图或列表求他恰好抽到景区A和景区B门票的概率.
23.某初中学校要新建一块篮球场地(如图所示),要求:①篮球场地的长和宽分别为28米和16米;②在篮球场地四周修建宽度相等的安全区域;③篮球场地及安全区域的总面积为.
(1)求安全区域的宽度.
(2)某公司希望用50万元承包这项工程,该单位认为金额太高需要降价,通过两次协商,最终以32万元达成一致.若两次降价的百分率相同,求每次降价的百分率.
24.如图,是同一水平线上的两点,无人机从点竖直上升到点时,测得到点的距离为点的俯角为,无人机继续竖直上升到点,测得点的俯角为.求无人机从点到点的上升高度(精确到).
参考数据:,,,,,.
如图,为的直径,点在上,点是直径上的一点(不与重合),过点作的垂线交的延长线于点.
(1)点在线段上,且.求证:是的切线;
(2)若,求的长.
26.某超市销售一种商品,进价为40元/千克,经市场调查,当售价为50元/千克时,每天可销售220千克;如果该商品每千克上涨1元,则每天可少卖10千克,规定每千克售价不能高于65元,且不能低于50元.设每千克商品的售价上涨元,每天的销售利润为元.
(1)设每天的销售量为千克,请写出与之间的函数关系式,并写出自变量的取值范围;
(2)求出与之间的函数关系式,当销售单价定为多少元时,该超市每天的利润最大?并求出此时的最大利润;
(3)若该超市销售该商品所获利润不低于2310元,请直接写出的取值范围.
27.【学习心得】
小雯同学在学习完“圆”这一章内容后,感觉到一些几何问题如果添加辅助圆,运用圆的知识解决,可以使问题变得非常容易.
例如:如图,在中,是外一点,且,求的度数.若以点为圆心,长为半径作辅助圆,则两点必在上,是的圆心角,是的圆周角,则.
(1)【初步运用】如图,在四边形中,,求的度数;
(2)【方法迁移】如图①,已知线段和直线,用直尺和圆规在上作出所有的点,使得(不写作法,保留作图痕迹);
图① 图② 图③
(3)【问题拓展】
(1)如图②,已知矩形为上的点.若满足的点恰好有两个,则的取值范围为
(2)如图③,在中,是边上的高,且,求的长.
28.如图,抛物线经过两点,并交轴于另一点,点是抛物线的顶点,直线与轴交于点.
(1)求该抛物线与直线的表达式;
(2)若点是轴上一动点,分别连接,求的最小值;
(3)若点是抛物线上一动点,问在对称轴上是否存在点,使得以为顶点的四边形是平行四边形?若存在,请直接写出所有满足条件的点的坐标;若不存在,请说明理由.
九年级数学练习答案
一、选择题(本大题共有8小题,每小题3分,共24分.在每小题所给出的四个选项中,恰有一项是符合题目要求的,请将正确选项前的字母代号涂在答题纸相应位置上)
题号 1 2 3 4 5 6 7 8
答案 C D B B A C C D
二、填空题(本大题共有10小题,每空3分,共30分.不需写出解答过程,请把答案直接填写在答题纸相应位置的横线上)
9.65 10.105 11.0.93 12.3 13.2011
14. 15. 16.或 17. 18.
三、解答题(共有9小题,共96分.解答时应写出必要的文字说明、证明过程或演算步骤)
19.(1)原式 (2)
20.(1)不论取何值,方程总有两个实数根.
(2)
解得
21.(1)2,2,2.5,(2)平均数 (3)3000
22.(1); (2) 图略
23.(1)解:设安全区域的宽度为米,由题意得
整理得解得(不符合题意,舍去)
(2)设每次降价的百分率为,由题意得解得(舍去),答略米
25.(1)连接,证
(2)
26.(1);
(2)当时最大,此时售价为56元,最大利润为2560元;(3)当时,解得,.
27.(1); (2)略; (3)①;②
(1)抛物线的表达式:,直线AM的表达式:;
(2); (3)点坐标为或或
一、选择题(本大题共8小题,每小题3分,共24分)
1.下列图案中是中心对称图形但不是轴对称图形的是( )
A. B. C. D.
2.若,则下列等式成立的是( )
A. B. C. D.
3.空气的成分(除去水汽、杂质等)是:氮气约占,氧气约占,其他微量气体约占.要反映上述信息,宜采用的统计图是( )
A.条形统计图 B.扇形统计图 C.折线统计图 D.频数分布直方图
4.已知的半径是6,点是平面内一点且,则点与的位置关系是( )
A.圆内 B.圆外 C.圆上 D.无法确定
5.在中,的值为( )
A. B. C. D.2
6.如图,是半径为2的上的三点,,则弦的长为( )
A.2 B.4 C. D.
7.根据下表可知,方程的一个解的范围为( )
…… 0.28 0.29 0.30 0.31 0.32 ……
…… 0.0261 0.0624 ……
A. B. C. D.
8.小明同学利用计算机软件绘制函数(为常数)的图象如图所示,由学习函数的经验,可以推断常数的值满足( )
A. B. C. D.
二、填空题(本大题共10小题,每小题3分,共30分)
9.2021年12月28日,连淮扬镇高铁正式运营,在比例尺为的工程示意图上,高邮站到扬州东站全长约为,它的实际长度约为________.
10.在中,若,则________.
11.某种绿豆在相同条件下发芽试验的结果如下:
每批粒数 50 100 500 1000 1500 2000 3000
发芽的频数 44 92 463 928 1396 1866 2794
发芽的频率 0.880 0.920 0.926 0.928 0.931 0.933 0.931
这种绿豆发芽的概率的估计值为________(精确到0.01).
12.如图,小明用图中的扇形纸片作一个圆锥的侧面,已知扇形的圆心角为,半径是,那么这个圆锥的底面半径是________.
13.若是关的方程的解,则的值为________.
14.点在抛物线上,则的大小关系是________(用“<”连接).
15.如图,是的直径,点在的延长线上,切于点,若,则的度数为________.
16.如图,已知二次函数与一次函数的图象相交于两点,则关于的不等式的解集为________.
17.如图,点在正方形的对角线上,于点,连接并延长,交边于点,交边的延长线于点.若,则________.
18.如图,是线段上一点,和是位于直线同侧的两个等边三角形.若,则四边形的面积最小值是________.
三、解答题(本大题共10小题,19-22每题8分,23-26每题10分,27-28每题12分,共96分)
19.(1)计算
(2)解方程:
20.已知关于的一元二次方程.
(1)求证:该方程总有两个实数根;
(2)若是该方程的两个实数根,且,求的取值范围.
21.国庆长假期间,兴趣小组随机采访了10位到高邮的游客使用“哈啰”共享电动车的次数,得到了这10位游客1天内使用“哈啰”共享电动车的次数,统计如下:
使用次数 0 2 3 4 6
人数 2 4 1 2 1
(1)这10位游客1天内使用“哈啰”共享电动车的次数的中位数是________次,众数是________次,平均数是________次;
(2)若小明同学把统计表中的数据“6”错看成了“5”,则用“街兔”共享电动车的次数的中位数、众数和平均数这三个统计量中受影响的是________;(填“中位数”、“众数”或“平均数”)
(3)若国庆长假期间,每天约有1200位游客到高邮,试估计这些游客国庆长假期间每天使用“哈啰”共享电动车的总次数.
22.为了深入推动大众旅游,满足人民群众美好生活需要,我市举办中国旅游日惠民周活动,活动主办方在活动现场提供免费门票抽奖箱,里面放有4张相同的卡片,分别写有景区:A.文游台,B.盂城驿,C.高邮当铺,D.龙虬庄遗址.抽奖规则如下:搅匀后从抽奖箱中任意抽取一张卡片,记录后放回,根据抽奖的结果获得相应的景区免费门票.
(1)小明获得一次抽奖机会,他恰好抽到景区A门票的概率是________.
(2)小亮获得两次抽奖机会,用树状图或列表求他恰好抽到景区A和景区B门票的概率.
23.某初中学校要新建一块篮球场地(如图所示),要求:①篮球场地的长和宽分别为28米和16米;②在篮球场地四周修建宽度相等的安全区域;③篮球场地及安全区域的总面积为.
(1)求安全区域的宽度.
(2)某公司希望用50万元承包这项工程,该单位认为金额太高需要降价,通过两次协商,最终以32万元达成一致.若两次降价的百分率相同,求每次降价的百分率.
24.如图,是同一水平线上的两点,无人机从点竖直上升到点时,测得到点的距离为点的俯角为,无人机继续竖直上升到点,测得点的俯角为.求无人机从点到点的上升高度(精确到).
参考数据:,,,,,.
如图,为的直径,点在上,点是直径上的一点(不与重合),过点作的垂线交的延长线于点.
(1)点在线段上,且.求证:是的切线;
(2)若,求的长.
26.某超市销售一种商品,进价为40元/千克,经市场调查,当售价为50元/千克时,每天可销售220千克;如果该商品每千克上涨1元,则每天可少卖10千克,规定每千克售价不能高于65元,且不能低于50元.设每千克商品的售价上涨元,每天的销售利润为元.
(1)设每天的销售量为千克,请写出与之间的函数关系式,并写出自变量的取值范围;
(2)求出与之间的函数关系式,当销售单价定为多少元时,该超市每天的利润最大?并求出此时的最大利润;
(3)若该超市销售该商品所获利润不低于2310元,请直接写出的取值范围.
27.【学习心得】
小雯同学在学习完“圆”这一章内容后,感觉到一些几何问题如果添加辅助圆,运用圆的知识解决,可以使问题变得非常容易.
例如:如图,在中,是外一点,且,求的度数.若以点为圆心,长为半径作辅助圆,则两点必在上,是的圆心角,是的圆周角,则.
(1)【初步运用】如图,在四边形中,,求的度数;
(2)【方法迁移】如图①,已知线段和直线,用直尺和圆规在上作出所有的点,使得(不写作法,保留作图痕迹);
图① 图② 图③
(3)【问题拓展】
(1)如图②,已知矩形为上的点.若满足的点恰好有两个,则的取值范围为
(2)如图③,在中,是边上的高,且,求的长.
28.如图,抛物线经过两点,并交轴于另一点,点是抛物线的顶点,直线与轴交于点.
(1)求该抛物线与直线的表达式;
(2)若点是轴上一动点,分别连接,求的最小值;
(3)若点是抛物线上一动点,问在对称轴上是否存在点,使得以为顶点的四边形是平行四边形?若存在,请直接写出所有满足条件的点的坐标;若不存在,请说明理由.
九年级数学练习答案
一、选择题(本大题共有8小题,每小题3分,共24分.在每小题所给出的四个选项中,恰有一项是符合题目要求的,请将正确选项前的字母代号涂在答题纸相应位置上)
题号 1 2 3 4 5 6 7 8
答案 C D B B A C C D
二、填空题(本大题共有10小题,每空3分,共30分.不需写出解答过程,请把答案直接填写在答题纸相应位置的横线上)
9.65 10.105 11.0.93 12.3 13.2011
14. 15. 16.或 17. 18.
三、解答题(共有9小题,共96分.解答时应写出必要的文字说明、证明过程或演算步骤)
19.(1)原式 (2)
20.(1)不论取何值,方程总有两个实数根.
(2)
解得
21.(1)2,2,2.5,(2)平均数 (3)3000
22.(1); (2) 图略
23.(1)解:设安全区域的宽度为米,由题意得
整理得解得(不符合题意,舍去)
(2)设每次降价的百分率为,由题意得解得(舍去),答略米
25.(1)连接,证
(2)
26.(1);
(2)当时最大,此时售价为56元,最大利润为2560元;(3)当时,解得,.
27.(1); (2)略; (3)①;②
(1)抛物线的表达式:,直线AM的表达式:;
(2); (3)点坐标为或或
同课章节目录
