数学人教A版(2019)必修第一册5.4三角函数的图象与性质 课件(共34张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册5.4三角函数的图象与性质 课件(共34张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-22 23:42:36 | ||
图片预览




文档简介
(共34张PPT)
人教版必修第一册A版
5.4《 三角函数的图像与性质 》
( 2 课 时 )
教学目标
学习目标:1.理解与掌握三角函数的图象与性质;
2.能灵活运用三角函数的图象与性质来求解相关的实际问题.
教学重点:三角函数的图象与性质.
教学难点:三角函数图象与性质的推导及其运用.
一
情景导入——单摆运动及其成像(导学)
(一)情景
简谐运动是最基本也是最简单的机械振动,单摆运动就是一种最常见的简谐振动.
一
情景导入——单摆运动及其成像(导学)
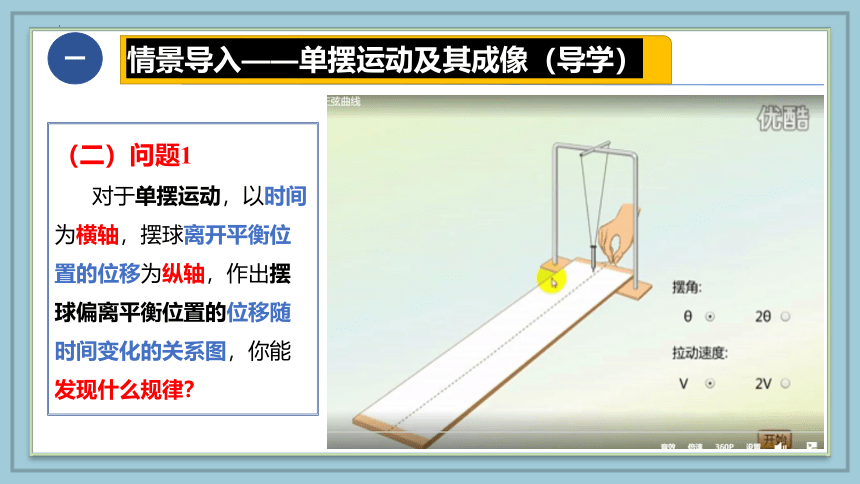
(二)问题1
对于单摆运动,以时间为横轴,摆球离开平衡位置的位移为纵轴,作出摆球偏离平衡位置的位移随时间变化的关系图,你能发现什么规律?
一
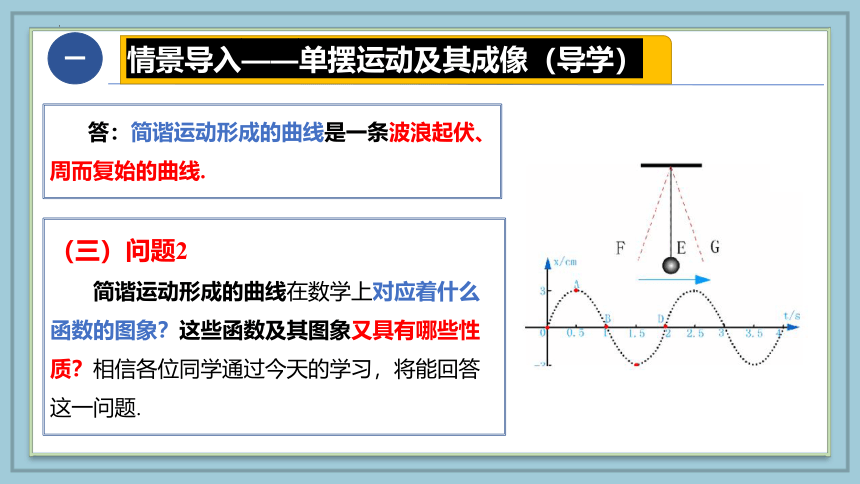
答:简谐运动形成的曲线是一条波浪起伏、周而复始的曲线.
情景导入——单摆运动及其成像(导学)
(三)问题2
简谐运动形成的曲线在数学上对应着什么函数的图象?这些函数及其图象又具有哪些性质?相信各位同学通过今天的学习,将能回答这一问题.
二
探究新知1——正弦函数的图象与性质(互学)
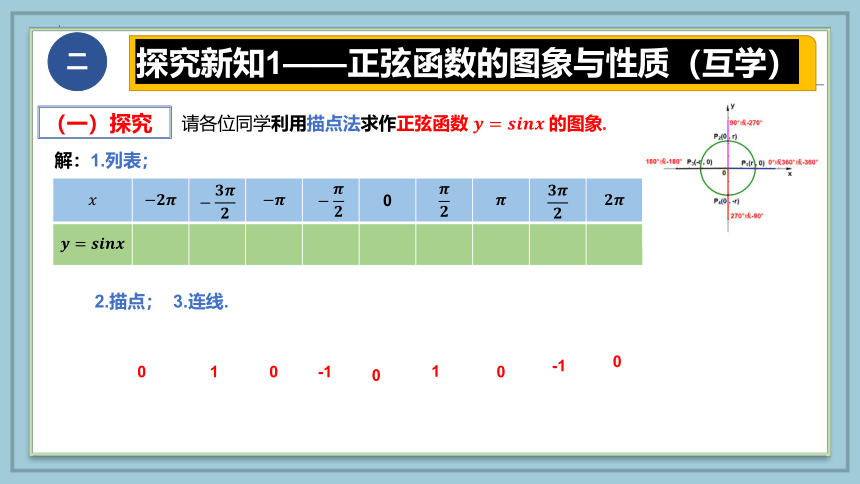
(一)探究
请各位同学利用描点法求作正弦函数 的图象.
解:1.列表;
0
0
1
0
-1
0
1
0
-1
0
2.描点; 3.连线.
二
探究新知1——正弦函数的图象与性质(互学)
(一)探究
请各位同学利用描点法求作正弦函数 的图象.
解:1.列表;
0
0
1
0
-1
0
1
0
-1
0
2.列表; 3.描点.
注:正弦函数的图象叫做正弦曲线,是一条“波浪起伏”的连续光滑曲线
二
探究新知1——正弦函数的图象与性质(互学)
(二)函数的周期性
1.周期函数
像正弦函数这样,
一般地,设函数的定义域为如果存在一个非零常数 ,
使得对于每一个 都有 ,且 成立
那么函数就叫做周期函数.
非零常数叫做这个函数的周期,周期函数的周期不止一个.
2.最小正周期
如果在周期函数的所有周期中存在一个最小的正数,那么这个最小正数就叫做的最小正周期
例如 对于正弦函数 ,
∵ ∴ 是周期函数,
都是它的周期,其中最小正周期为
二
探究新知1——正弦函数的图象与性质(互学)
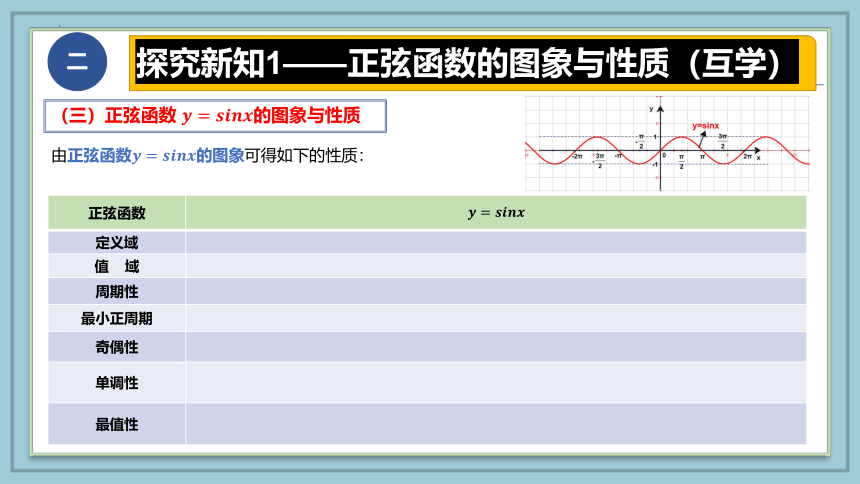
(三)正弦函数 的图象与性质
由正弦函数的图象可得如下的性质:
正弦函数
定义域
值 域
周期性
最小正周期
奇偶性
单调性
最值性
二
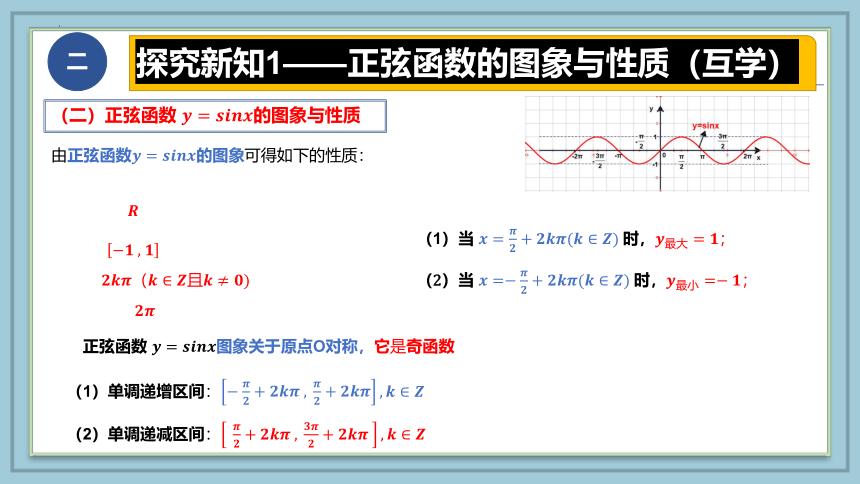
探究新知1——正弦函数的图象与性质(互学)
(二)正弦函数 的图象与性质
由正弦函数的图象可得如下的性质:
正弦函数 图象关于原点O对称,它是奇函数
(1)单调递增区间:
(2)单调递减区间:
(1)当 时,
(2)当 时,
三
探究新知2——余弦函数的图象与性质(互学)
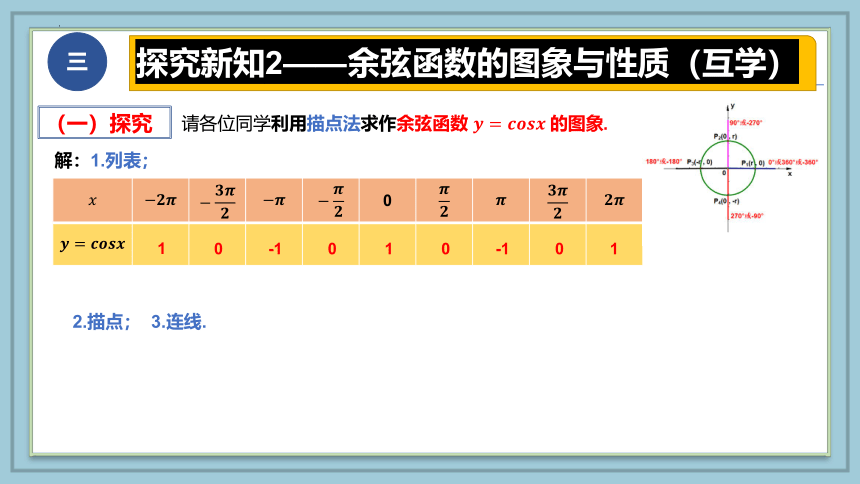
(一)探究
请各位同学利用描点法求作余弦函数 的图象.
解:1.列表;
0
1
0
-1
0
1
0
-1
0
1
2.描点; 3.连线.
三
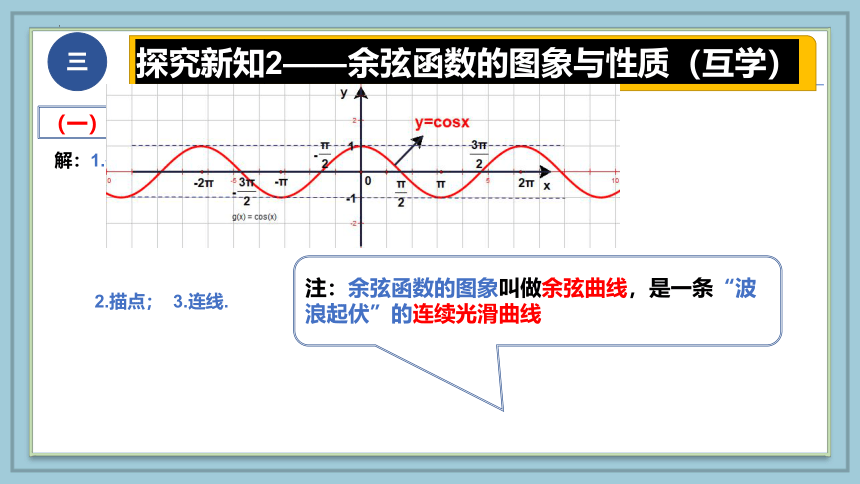
探究新知2——余弦函数的图象与性质(互学)
(一)探究
请各位同学利用描点法求作正弦函数 的图象.
解:1.列表;
2.描点; 3.连线.
注:余弦函数的图象叫做余弦曲线,是一条“波浪起伏”的连续光滑曲线
三
探究新知2——余弦函数的图象与性质(互学)
(二)余弦函数 的图象与性质
由余弦函数的图象可得如下的性质:
余弦函数
定义域
值 域
周期性
最小正周期
奇偶性
单调性
最值性
三
探究新知2——余弦函数的图象与性质(互学)
(二)余弦函数 的图象与性质
由余弦函数的图象可得如下的性质:
余弦函数的图象关于轴对称,它是偶函数
(1)单调递增区间:;
(2)单调递减区间: .
(1)当 时,
(2)当 时,
四
探究新知3——正切函数的图象与性质(互学)
(一)探究
请各位同学利用描点法求作正切函数 的图象.
解:1.列表;
0
无意义
-1
1
0
无意义
四
探究新知3——正切函数的图象与性质(互学)
(一)探究
请各位同学利用描点法求作正切函数 的图象.
解:1.列表;
0
无意义
-1
1
0
无意义
四
探究新知3——正切函数的图象与性质(互学)
(一)探究
请各位同学利用描点法求作正切函数 的图象.
解:1.列表;
2.描点; 3.连线.
注:正切函数的图象叫做正切曲线,正切曲线是被与轴平行的一系列直线所隔开的无穷多支形状相同的曲线组成的.
四
探究新知3——正切函数的图象与性质(互学)
(二)正切函数 的图象与性质
由正切函数的图象可得如下的性质:
正切函数
定义域
值 域
最小正周期
奇偶性
单调性
对称性
四
探究新知3——正切函数的图象与性质(互学)
(二)正切函数 的图象与性质
由正切函数 的图象可得如下的性质:
正切函数 的图象关于原点O对称,它是奇函数
单调递增区间:
对称中心为
五
小组合作、讨论交流1(自学)
各位同学,请大家每4个人组成一组,分别交流讨论后,解决下列问题:
方法提示:本题考察了利用描点法求作三角函数的图象.
例1 请用描点法画出下列函数的图象;
(1);
(2) ;
六
成果展示1 (迁移变通)
例1 请用描点法画出下列函数的图象; (1);
解:1.列表;
0
0
1
0
-1
0
1
2
1
0
1
2.列表; 3.描点.
六
成果展示1 (迁移变通)
例1 请用描点法画出下列函数的图象; (2)
解:1.列表;
1
0
-1
0
1
-1
0
1
0
-1
2.列表; 3.描点.
0
-1
七
小组合作、讨论交流2(自学)
各位同学,请大家每4个人组成一组,分别交流讨论后,解决下列问题:
方法提示:本题考察了三角函数函数的周期性.
例2 求下列函数的周期
(1); (2) ;
(3)
提示:今后本书中所涉及的周期,如果不加特别说明,一般都是指函数的最小正周期.
八
成果展示2(迁移变通)
例2 求下列函数的周期
(1); (2) ; (3)
解(1)
∵对于 , 都有
即满足
∴原函数的周期为.
解(2)令 (换元法)
∵对于 , 都有
且
即
∴ 满足
故原函数的周期为.
解(3)令 (换元法)
∵对于 , 都有
且
即
∴ 满足
故原函数的周期为.
九
小组合作、讨论交流3(自学)
各位同学,请大家每4个人组成一组,分别交流讨论后,解决下列问题:
例3 下列函数有最大值、最小值吗?如果有,请写出取最大值、最小值时自变量的集合,并求出最大值、最小值.
(1); (2) ;
例4 不通过求值,比较下列各组数的大小:
(1); (2) ;
方法提示:本题考察了三角函数函数的最值性与单调性.
十
成果展示3(迁移变通)
例3 下列函数有最大值、最小值吗?如果有,请写出取最大值、最小值时自变量的集合,并求出最大值、最小值.
(1);
解(1)
∵ 对于 , 都有
∴ 0
故当 时,
当 时,
十
解(2)令 则 (换元法)
∵ 对于 , 都有
且
∴ 3
故当 ,
即 时
例3 下列函数有最大值、最小值吗?如果有,请写出取最大值、最小值时自变量的集合,并求出最大值、最小值.
(2) ;
故当 ,
即 时
成果展示3(迁移变通)
十
解(1)
∵
而正弦函数在区间上单调递增
∴
例4 不通过求值,比较下列各组数的大小:
(1);
成果展示3(迁移变通)
十
例4 不通过求值,比较下列各组数的大小:
(2) ;
解(2)
∵
又∵
而余弦函数在区间上单调递减
∴
即
成果展示3(迁移变通)
十一
提升演练(检测实践)
例5 求函数 的单调递增区间.
解(换元法):
令 ,则
∵已知,即
∴
即
又∵的单调递增区间为
且由 可得
(还原法)
∴ 的单调递增区间为
十一
提升演练(检测实践)
例6 求函数 的定义域、周期及单调性.
解(换元法):
令 ,则
∵对于 ,
∴
即
故原函数的定义域为
又∵
∴
即满足
故原函数的周期为
又∵ 的单调递增区间为
且由 可得
(还原法)
∴ 的单调递增区间为
课堂小结
八
今天我们学习了哪些内容?
1.理解与掌握了三角函数的图象与性质;
2.能灵活运用三角函数的图象与性质来求解相关的实际问题.
九
学生自评
请小老师组对所负责组员的课堂表现进行评价
十
家庭作业
1.完成《高考领航》第123-133页知识点填空;
2.完成《课时规范训练》第64-70页题型.
人教版必修第一册A版
5.4《 三角函数的图像与性质 》
( 2 课 时 )
教学目标
学习目标:1.理解与掌握三角函数的图象与性质;
2.能灵活运用三角函数的图象与性质来求解相关的实际问题.
教学重点:三角函数的图象与性质.
教学难点:三角函数图象与性质的推导及其运用.
一
情景导入——单摆运动及其成像(导学)
(一)情景
简谐运动是最基本也是最简单的机械振动,单摆运动就是一种最常见的简谐振动.
一
情景导入——单摆运动及其成像(导学)
(二)问题1
对于单摆运动,以时间为横轴,摆球离开平衡位置的位移为纵轴,作出摆球偏离平衡位置的位移随时间变化的关系图,你能发现什么规律?
一
答:简谐运动形成的曲线是一条波浪起伏、周而复始的曲线.
情景导入——单摆运动及其成像(导学)
(三)问题2
简谐运动形成的曲线在数学上对应着什么函数的图象?这些函数及其图象又具有哪些性质?相信各位同学通过今天的学习,将能回答这一问题.
二
探究新知1——正弦函数的图象与性质(互学)
(一)探究
请各位同学利用描点法求作正弦函数 的图象.
解:1.列表;
0
0
1
0
-1
0
1
0
-1
0
2.描点; 3.连线.
二
探究新知1——正弦函数的图象与性质(互学)
(一)探究
请各位同学利用描点法求作正弦函数 的图象.
解:1.列表;
0
0
1
0
-1
0
1
0
-1
0
2.列表; 3.描点.
注:正弦函数的图象叫做正弦曲线,是一条“波浪起伏”的连续光滑曲线
二
探究新知1——正弦函数的图象与性质(互学)
(二)函数的周期性
1.周期函数
像正弦函数这样,
一般地,设函数的定义域为如果存在一个非零常数 ,
使得对于每一个 都有 ,且 成立
那么函数就叫做周期函数.
非零常数叫做这个函数的周期,周期函数的周期不止一个.
2.最小正周期
如果在周期函数的所有周期中存在一个最小的正数,那么这个最小正数就叫做的最小正周期
例如 对于正弦函数 ,
∵ ∴ 是周期函数,
都是它的周期,其中最小正周期为
二
探究新知1——正弦函数的图象与性质(互学)
(三)正弦函数 的图象与性质
由正弦函数的图象可得如下的性质:
正弦函数
定义域
值 域
周期性
最小正周期
奇偶性
单调性
最值性
二
探究新知1——正弦函数的图象与性质(互学)
(二)正弦函数 的图象与性质
由正弦函数的图象可得如下的性质:
正弦函数 图象关于原点O对称,它是奇函数
(1)单调递增区间:
(2)单调递减区间:
(1)当 时,
(2)当 时,
三
探究新知2——余弦函数的图象与性质(互学)
(一)探究
请各位同学利用描点法求作余弦函数 的图象.
解:1.列表;
0
1
0
-1
0
1
0
-1
0
1
2.描点; 3.连线.
三
探究新知2——余弦函数的图象与性质(互学)
(一)探究
请各位同学利用描点法求作正弦函数 的图象.
解:1.列表;
2.描点; 3.连线.
注:余弦函数的图象叫做余弦曲线,是一条“波浪起伏”的连续光滑曲线
三
探究新知2——余弦函数的图象与性质(互学)
(二)余弦函数 的图象与性质
由余弦函数的图象可得如下的性质:
余弦函数
定义域
值 域
周期性
最小正周期
奇偶性
单调性
最值性
三
探究新知2——余弦函数的图象与性质(互学)
(二)余弦函数 的图象与性质
由余弦函数的图象可得如下的性质:
余弦函数的图象关于轴对称,它是偶函数
(1)单调递增区间:;
(2)单调递减区间: .
(1)当 时,
(2)当 时,
四
探究新知3——正切函数的图象与性质(互学)
(一)探究
请各位同学利用描点法求作正切函数 的图象.
解:1.列表;
0
无意义
-1
1
0
无意义
四
探究新知3——正切函数的图象与性质(互学)
(一)探究
请各位同学利用描点法求作正切函数 的图象.
解:1.列表;
0
无意义
-1
1
0
无意义
四
探究新知3——正切函数的图象与性质(互学)
(一)探究
请各位同学利用描点法求作正切函数 的图象.
解:1.列表;
2.描点; 3.连线.
注:正切函数的图象叫做正切曲线,正切曲线是被与轴平行的一系列直线所隔开的无穷多支形状相同的曲线组成的.
四
探究新知3——正切函数的图象与性质(互学)
(二)正切函数 的图象与性质
由正切函数的图象可得如下的性质:
正切函数
定义域
值 域
最小正周期
奇偶性
单调性
对称性
四
探究新知3——正切函数的图象与性质(互学)
(二)正切函数 的图象与性质
由正切函数 的图象可得如下的性质:
正切函数 的图象关于原点O对称,它是奇函数
单调递增区间:
对称中心为
五
小组合作、讨论交流1(自学)
各位同学,请大家每4个人组成一组,分别交流讨论后,解决下列问题:
方法提示:本题考察了利用描点法求作三角函数的图象.
例1 请用描点法画出下列函数的图象;
(1);
(2) ;
六
成果展示1 (迁移变通)
例1 请用描点法画出下列函数的图象; (1);
解:1.列表;
0
0
1
0
-1
0
1
2
1
0
1
2.列表; 3.描点.
六
成果展示1 (迁移变通)
例1 请用描点法画出下列函数的图象; (2)
解:1.列表;
1
0
-1
0
1
-1
0
1
0
-1
2.列表; 3.描点.
0
-1
七
小组合作、讨论交流2(自学)
各位同学,请大家每4个人组成一组,分别交流讨论后,解决下列问题:
方法提示:本题考察了三角函数函数的周期性.
例2 求下列函数的周期
(1); (2) ;
(3)
提示:今后本书中所涉及的周期,如果不加特别说明,一般都是指函数的最小正周期.
八
成果展示2(迁移变通)
例2 求下列函数的周期
(1); (2) ; (3)
解(1)
∵对于 , 都有
即满足
∴原函数的周期为.
解(2)令 (换元法)
∵对于 , 都有
且
即
∴ 满足
故原函数的周期为.
解(3)令 (换元法)
∵对于 , 都有
且
即
∴ 满足
故原函数的周期为.
九
小组合作、讨论交流3(自学)
各位同学,请大家每4个人组成一组,分别交流讨论后,解决下列问题:
例3 下列函数有最大值、最小值吗?如果有,请写出取最大值、最小值时自变量的集合,并求出最大值、最小值.
(1); (2) ;
例4 不通过求值,比较下列各组数的大小:
(1); (2) ;
方法提示:本题考察了三角函数函数的最值性与单调性.
十
成果展示3(迁移变通)
例3 下列函数有最大值、最小值吗?如果有,请写出取最大值、最小值时自变量的集合,并求出最大值、最小值.
(1);
解(1)
∵ 对于 , 都有
∴ 0
故当 时,
当 时,
十
解(2)令 则 (换元法)
∵ 对于 , 都有
且
∴ 3
故当 ,
即 时
例3 下列函数有最大值、最小值吗?如果有,请写出取最大值、最小值时自变量的集合,并求出最大值、最小值.
(2) ;
故当 ,
即 时
成果展示3(迁移变通)
十
解(1)
∵
而正弦函数在区间上单调递增
∴
例4 不通过求值,比较下列各组数的大小:
(1);
成果展示3(迁移变通)
十
例4 不通过求值,比较下列各组数的大小:
(2) ;
解(2)
∵
又∵
而余弦函数在区间上单调递减
∴
即
成果展示3(迁移变通)
十一
提升演练(检测实践)
例5 求函数 的单调递增区间.
解(换元法):
令 ,则
∵已知,即
∴
即
又∵的单调递增区间为
且由 可得
(还原法)
∴ 的单调递增区间为
十一
提升演练(检测实践)
例6 求函数 的定义域、周期及单调性.
解(换元法):
令 ,则
∵对于 ,
∴
即
故原函数的定义域为
又∵
∴
即满足
故原函数的周期为
又∵ 的单调递增区间为
且由 可得
(还原法)
∴ 的单调递增区间为
课堂小结
八
今天我们学习了哪些内容?
1.理解与掌握了三角函数的图象与性质;
2.能灵活运用三角函数的图象与性质来求解相关的实际问题.
九
学生自评
请小老师组对所负责组员的课堂表现进行评价
十
家庭作业
1.完成《高考领航》第123-133页知识点填空;
2.完成《课时规范训练》第64-70页题型.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
