数学人教A版(2019)必修第一册4.3对数 课件(共32张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册4.3对数 课件(共32张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 14.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-22 23:50:20 | ||
图片预览











文档简介
(共32张PPT)
人教版必修第一册A版
4.3《 对 数 》
( 4 课 时 )
教学目标
学习目标:1.认识与理解对数的概念;
2.理解与掌握对数的性质、分类及其运算法则,并能运用其求解相关的实际问题.
教学重点:对数的概念、性质、分类及其运算法则;
教学难点:对数运算法则的实际运用.
一
情景问题(导学)
(一)情
景 水
污
染
治
理
一
情景问题(导学)
如果某市一段河道河水开始的污染程度设为1,经过治理后,河水污染程度 与治理时间 (年)的关系为
那么当该河道河水污染程度变为原来的时,需要治理多长时间?
(二)问题
一
情景问题(导学)
如果某市一段河流河水开始的污染程度设为1,经过治理后,河水污染程度 与治理时间 (年)的关系为
那么当污染程度为原来的时,需要治理多长时间?
(三)分析
分析:∵ 已知河水污染程度 与治理时间 (年)的关系为
当污染程度为原来的时,即
∴ 满足
注:要求河水的治理时间(年),即求式子中的指数的值为多少?
那么我们应该如何来求解这一式子中的指数?求解指数的运算数学上叫什么运算?相信各位同学通过今天的学习,将能回答这些问题.
二
探究新知1——对数的概念、分类及其性质(互学)
一般地,如果,则称为以为底的对数,记作
其中称为对数的底数,称为真数(且).
例如:∵
∴
再如:∵
∴
(一)对数的概念
二
探究新知1——对数的概念、分类及其性质(互学)
当且时,指数式与对数式的关系为
(二)对数式与指数式的关系
①
②
③
据对数的定义可知:
①指数式中的指数就是对数式的结果;
②指数式的结果就是对数式中的真数;
③指数式中的底数就是对数式中的底数;
注:由指数与对数的关系可知——
指数运算与对数运算互为逆运算.
二
探究新知1——对数的概念、分类及其性质(互学)
(三)对数的分类
1.普通对数: ;
例如 ( ∵ )
2.常用对数:以10为底的对数称为常用对数,并把记作,即
例如 ( ∵ ),( ∵ )
3.自然对数:在科学研究和工程计算中,经常使用以无理数 e (e=2.71828…) 为底的对数,以e为底的对数称为自然对数,简记为即
例如 .
二
探究新知1——对数的概念、分类及其性质(互学)
(四)对数的性质
1.性质1: (即真数为1的对数等于0) ;
分析: ∵
∴
2.性质2: (即真数与底数相同的对数等于1) ;
分析: ∵
∴
二
探究新知1——对数的概念、分类及其性质(互学)
(四)对数的性质
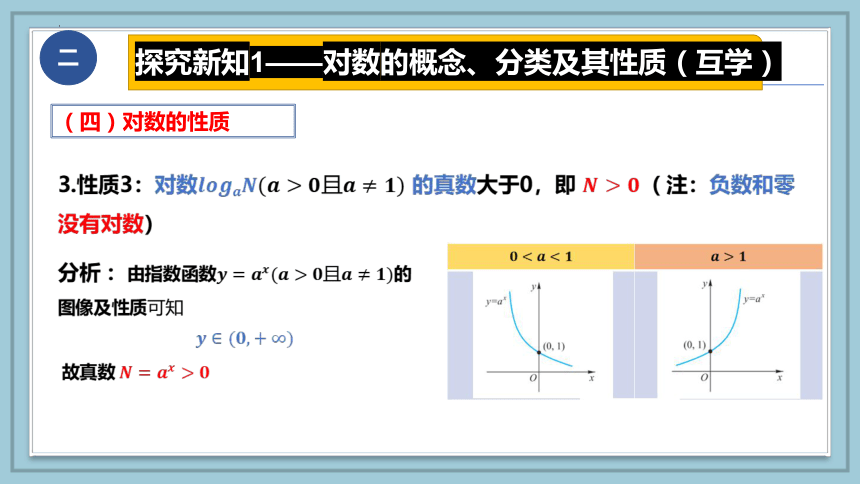
3.性质3:对数的真数大于0,即 ( 注:负数和零没有对数)
分析 :由指数函数的图像及性质可知
故真数
三
小组合作、讨论交流1(自学)
例1 把下列指数式化为对数式,对数式化为指数式.
(1); (2); (3)
(4) ; (5) ; (6)
各位同学,请大家每4个人组成一组,分别交流讨论后,解决下列问题:
四
成果展示1(迁移变通)
例1 把下列指数式化为对数式,对数式化为指数式.
(1); (2); (3)
解(1):
∵ 已知指数式
∴ 可得对数式为
解(2):
∵ 已知指数式
∴ 可得对数式为
解(3):
∵ 已知指数式
∴ 可得对数式为
四
成果展示1(迁移变通)
解(4):
∵ 已知对数式
∴ 可得指数式为
例1 把下列指数式化为对数式,对数式化为指数式.
(4) ; (5) ; (6)
解(5):
∵ 已知对数式
∴ 可得指数式为
解(6):
∵ 已知对数式
∴ 可得指数式为
五
小组合作、讨论交流2(自学)
例2 求下列对数式的值.
(1); (2); (3); (4)
各位同学,请大家每4个人组成一组,分别交流讨论后,解决下列问题:
六
成果展示2(迁移变通)
解(1):
∵ 指数式
∴ 对数式
例2 求下列对数式的值.
(1); (2); (3); (4)
解(2):
∵ 指数式
∴ 对数式
解(3):
∵ 指数式
∴ 对数式
解(4):
∵ 指数式
∴ 对数式
例3 求下列各对数式中的值.
(1);(2); (3); (4)
各位同学,请大家每4个人组成一组,分别交流讨论后,解决下列问题:
七
提升演练1(检测实践)
例4 情景问题:
如果某市一段河流河水开始的污染程度设为1,经过治理后,河水污染程度 与治理时间 (年)的关系为
那么当污染程度为原来的时,需要治理多长时间?
七
提升演练1(检测实践)
解(1):
∵ 已知
∴
故
例3 求下列各对数式中的值.
(1);(2); (3); (4)
解(2):
∵ 已知
∴
∴
故
七
提升演练1(检测实践)
解(3):
∵
∴
故
例3 求下列各对数式中的值.
(1);(2); (3); (4)
解法一(4):
∵ 已知
∴
∴
∴
故
解法二(4):
∵
∴
故
七
提升演练1(检测实践)
例4 情景问题:
如果某市一段河流河水开始的污染程度设为1,经过治理后,河水污染程度 与治理时间 (年)的关系为
那么当污染程度为原来的时,需要治理多长时间?
解:∵ 已知河水污染程度 与治理时间 (年)的关系为
当污染程度为原来的时,即
∴ 满足
∴
答:当污染程度为原来的时,
需要治理约7.2年的时间.
八
探究新知2——对数的运算法则(导学)
(一)法则1:积化和公式
如果 且 , 那么
探究:设
则有
∵
∴
即 成立
注:注意运用时公式的逆用(和化积公式)
八
探究新知2——对数的运算法则(导学)
(二)法则2:商化差公式
如果 且 , 那么
探究:设
则有
∵
∴
即 成立
注:注意运用时公式的逆用(差化商公式)
八
探究新知2——对数的运算法则(导学)
(三)法则3:幂的对数公式(指数提前性)
如果 且 , 那么
探究:设
则有
∵
∴ np
即 成立
注:注意运用时公式的逆用(系数置后指数性)
八
探究新知2——对数的运算法则(导学)
(四)法则4:换底公式
如果 且 , 且, 那么
探究:设
于是
∴ 据指数提前性可得:
∴
即成立
注:注意运用时公式的逆用
八
探究新知2——对数的运算法则(导学)
(五)法则5:倒数性
, 或 =1
如果 且且, 那么
探究:设 ,且
于是据换底公式可得
,
∴
即成立
注:注意运用时公式的逆用
八
探究新知2——对数的运算法则(导学)
小 结
(一)法则1:积化和公式
(二)法则2:商化差公式
(三)法则3:幂的对数公式(指数提前性)
(四)法则4:换底公式
(五)法则5:倒数性
, 或 =1
九
小组合作、讨论交流3(自学)
各位同学,请大家每4个人组成一组,分别交流讨论后,解决下列问题:
例5 求下列各式的值.
(1); (2).
例6 用表示 , 其中
十
成果展示3(迁移变通)
例5 求下列各式的值.
(1); (2).
解(1):
(指数提前性)
解(2):
十
成果展示3(迁移变通)
解:∵ 已知
∴ (商化差公式)
(积化和公式)
(指数提前性)
例6 用表示 , 其中
十一
提升演练(检测实践)
例7 尽管目前人类还无法准确预报地震,但科学家通过研究,已经对地震有所了解.例如,地震时释放出的能量 (单位:焦耳)与地震里氏震级 之间的关系为
2011年3月11日,日本东北部海域发生里氏9.0级地震,它所释放出来的能量是2008年5月12日我国汶川发生里氏8.0级地震的多少倍(精确到1)
解:设里氏9.0级和8.0级地震的能量分别为和
∵ 已知
∴ (焦耳)
(焦耳)
于是
∴
答:日本东北部海域发生里氏9.0级地震,它所释放出来的能量约是2008年5月12日我国汶川发生里氏8.0级地震的32倍
课堂小结
十二
1.认识与理解对数的概念;
2.理解与掌握对数的性质、分类及其运算法则,并能运用其求解相关的实际问题.
十三
学生自评
十四
家庭作业
1.记背今天所学习对数的相关知识;
2.完成《课时规范训练》第41、42页的相关题型.
人教版必修第一册A版
4.3《 对 数 》
( 4 课 时 )
教学目标
学习目标:1.认识与理解对数的概念;
2.理解与掌握对数的性质、分类及其运算法则,并能运用其求解相关的实际问题.
教学重点:对数的概念、性质、分类及其运算法则;
教学难点:对数运算法则的实际运用.
一
情景问题(导学)
(一)情
景 水
污
染
治
理
一
情景问题(导学)
如果某市一段河道河水开始的污染程度设为1,经过治理后,河水污染程度 与治理时间 (年)的关系为
那么当该河道河水污染程度变为原来的时,需要治理多长时间?
(二)问题
一
情景问题(导学)
如果某市一段河流河水开始的污染程度设为1,经过治理后,河水污染程度 与治理时间 (年)的关系为
那么当污染程度为原来的时,需要治理多长时间?
(三)分析
分析:∵ 已知河水污染程度 与治理时间 (年)的关系为
当污染程度为原来的时,即
∴ 满足
注:要求河水的治理时间(年),即求式子中的指数的值为多少?
那么我们应该如何来求解这一式子中的指数?求解指数的运算数学上叫什么运算?相信各位同学通过今天的学习,将能回答这些问题.
二
探究新知1——对数的概念、分类及其性质(互学)
一般地,如果,则称为以为底的对数,记作
其中称为对数的底数,称为真数(且).
例如:∵
∴
再如:∵
∴
(一)对数的概念
二
探究新知1——对数的概念、分类及其性质(互学)
当且时,指数式与对数式的关系为
(二)对数式与指数式的关系
①
②
③
据对数的定义可知:
①指数式中的指数就是对数式的结果;
②指数式的结果就是对数式中的真数;
③指数式中的底数就是对数式中的底数;
注:由指数与对数的关系可知——
指数运算与对数运算互为逆运算.
二
探究新知1——对数的概念、分类及其性质(互学)
(三)对数的分类
1.普通对数: ;
例如 ( ∵ )
2.常用对数:以10为底的对数称为常用对数,并把记作,即
例如 ( ∵ ),( ∵ )
3.自然对数:在科学研究和工程计算中,经常使用以无理数 e (e=2.71828…) 为底的对数,以e为底的对数称为自然对数,简记为即
例如 .
二
探究新知1——对数的概念、分类及其性质(互学)
(四)对数的性质
1.性质1: (即真数为1的对数等于0) ;
分析: ∵
∴
2.性质2: (即真数与底数相同的对数等于1) ;
分析: ∵
∴
二
探究新知1——对数的概念、分类及其性质(互学)
(四)对数的性质
3.性质3:对数的真数大于0,即 ( 注:负数和零没有对数)
分析 :由指数函数的图像及性质可知
故真数
三
小组合作、讨论交流1(自学)
例1 把下列指数式化为对数式,对数式化为指数式.
(1); (2); (3)
(4) ; (5) ; (6)
各位同学,请大家每4个人组成一组,分别交流讨论后,解决下列问题:
四
成果展示1(迁移变通)
例1 把下列指数式化为对数式,对数式化为指数式.
(1); (2); (3)
解(1):
∵ 已知指数式
∴ 可得对数式为
解(2):
∵ 已知指数式
∴ 可得对数式为
解(3):
∵ 已知指数式
∴ 可得对数式为
四
成果展示1(迁移变通)
解(4):
∵ 已知对数式
∴ 可得指数式为
例1 把下列指数式化为对数式,对数式化为指数式.
(4) ; (5) ; (6)
解(5):
∵ 已知对数式
∴ 可得指数式为
解(6):
∵ 已知对数式
∴ 可得指数式为
五
小组合作、讨论交流2(自学)
例2 求下列对数式的值.
(1); (2); (3); (4)
各位同学,请大家每4个人组成一组,分别交流讨论后,解决下列问题:
六
成果展示2(迁移变通)
解(1):
∵ 指数式
∴ 对数式
例2 求下列对数式的值.
(1); (2); (3); (4)
解(2):
∵ 指数式
∴ 对数式
解(3):
∵ 指数式
∴ 对数式
解(4):
∵ 指数式
∴ 对数式
例3 求下列各对数式中的值.
(1);(2); (3); (4)
各位同学,请大家每4个人组成一组,分别交流讨论后,解决下列问题:
七
提升演练1(检测实践)
例4 情景问题:
如果某市一段河流河水开始的污染程度设为1,经过治理后,河水污染程度 与治理时间 (年)的关系为
那么当污染程度为原来的时,需要治理多长时间?
七
提升演练1(检测实践)
解(1):
∵ 已知
∴
故
例3 求下列各对数式中的值.
(1);(2); (3); (4)
解(2):
∵ 已知
∴
∴
故
七
提升演练1(检测实践)
解(3):
∵
∴
故
例3 求下列各对数式中的值.
(1);(2); (3); (4)
解法一(4):
∵ 已知
∴
∴
∴
故
解法二(4):
∵
∴
故
七
提升演练1(检测实践)
例4 情景问题:
如果某市一段河流河水开始的污染程度设为1,经过治理后,河水污染程度 与治理时间 (年)的关系为
那么当污染程度为原来的时,需要治理多长时间?
解:∵ 已知河水污染程度 与治理时间 (年)的关系为
当污染程度为原来的时,即
∴ 满足
∴
答:当污染程度为原来的时,
需要治理约7.2年的时间.
八
探究新知2——对数的运算法则(导学)
(一)法则1:积化和公式
如果 且 , 那么
探究:设
则有
∵
∴
即 成立
注:注意运用时公式的逆用(和化积公式)
八
探究新知2——对数的运算法则(导学)
(二)法则2:商化差公式
如果 且 , 那么
探究:设
则有
∵
∴
即 成立
注:注意运用时公式的逆用(差化商公式)
八
探究新知2——对数的运算法则(导学)
(三)法则3:幂的对数公式(指数提前性)
如果 且 , 那么
探究:设
则有
∵
∴ np
即 成立
注:注意运用时公式的逆用(系数置后指数性)
八
探究新知2——对数的运算法则(导学)
(四)法则4:换底公式
如果 且 , 且, 那么
探究:设
于是
∴ 据指数提前性可得:
∴
即成立
注:注意运用时公式的逆用
八
探究新知2——对数的运算法则(导学)
(五)法则5:倒数性
, 或 =1
如果 且且, 那么
探究:设 ,且
于是据换底公式可得
,
∴
即成立
注:注意运用时公式的逆用
八
探究新知2——对数的运算法则(导学)
小 结
(一)法则1:积化和公式
(二)法则2:商化差公式
(三)法则3:幂的对数公式(指数提前性)
(四)法则4:换底公式
(五)法则5:倒数性
, 或 =1
九
小组合作、讨论交流3(自学)
各位同学,请大家每4个人组成一组,分别交流讨论后,解决下列问题:
例5 求下列各式的值.
(1); (2).
例6 用表示 , 其中
十
成果展示3(迁移变通)
例5 求下列各式的值.
(1); (2).
解(1):
(指数提前性)
解(2):
十
成果展示3(迁移变通)
解:∵ 已知
∴ (商化差公式)
(积化和公式)
(指数提前性)
例6 用表示 , 其中
十一
提升演练(检测实践)
例7 尽管目前人类还无法准确预报地震,但科学家通过研究,已经对地震有所了解.例如,地震时释放出的能量 (单位:焦耳)与地震里氏震级 之间的关系为
2011年3月11日,日本东北部海域发生里氏9.0级地震,它所释放出来的能量是2008年5月12日我国汶川发生里氏8.0级地震的多少倍(精确到1)
解:设里氏9.0级和8.0级地震的能量分别为和
∵ 已知
∴ (焦耳)
(焦耳)
于是
∴
答:日本东北部海域发生里氏9.0级地震,它所释放出来的能量约是2008年5月12日我国汶川发生里氏8.0级地震的32倍
课堂小结
十二
1.认识与理解对数的概念;
2.理解与掌握对数的性质、分类及其运算法则,并能运用其求解相关的实际问题.
十三
学生自评
十四
家庭作业
1.记背今天所学习对数的相关知识;
2.完成《课时规范训练》第41、42页的相关题型.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
