2015年秋湘教版八年级数学上册课件2.1 三角形(45张PPT)
文档属性
| 名称 | 2015年秋湘教版八年级数学上册课件2.1 三角形(45张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-09-20 19:59:38 | ||
图片预览







文档简介
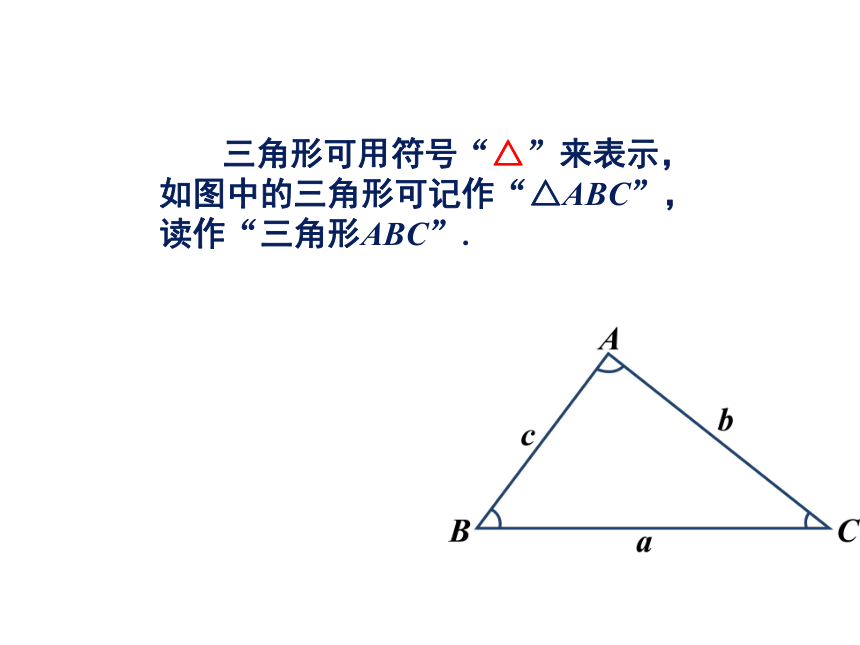
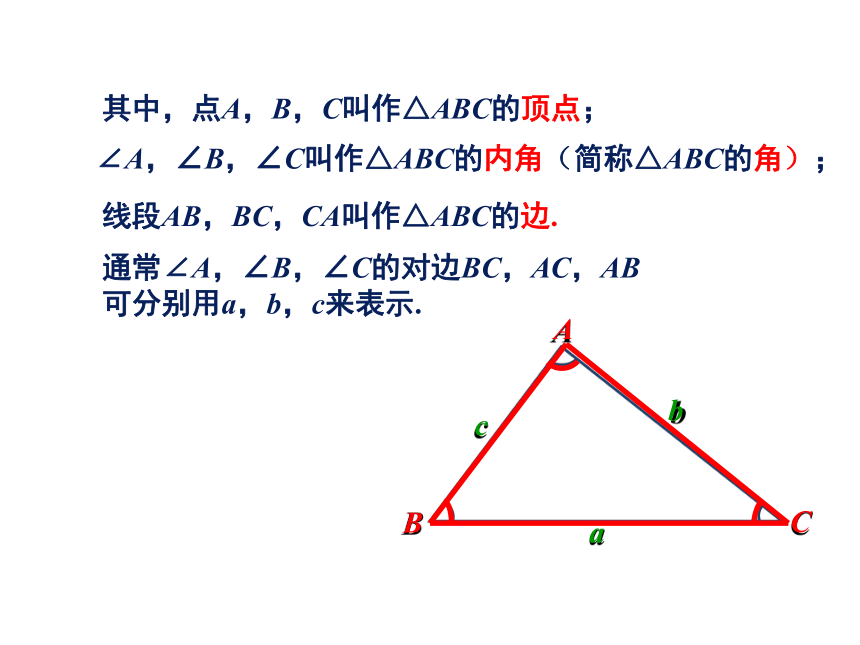
课件45张PPT。2.1三角形 观察下图,找一找图中的三角形,并把它们勾画出来. 你还能举出一些实例吗?定义:不在同一直线上的三条线段首尾相接所构成的图形叫作三角形. 三角形可用符号“△”来表示,如图中的三角形可记作“△ABC”,读作“三角形ABC”.其中,点A,B,C叫作△ABC的顶点;∠A,∠B,∠C叫作△ABC的内角(简称△ABC的角);线段AB,BC,CA叫作△ABC的边.通常∠A,∠B,∠C的对边BC,AC,AB
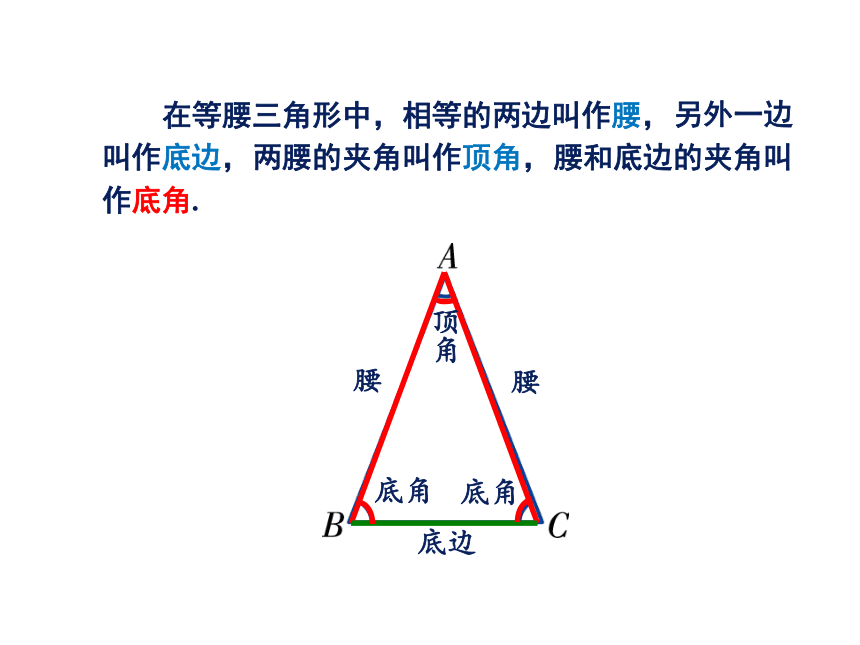
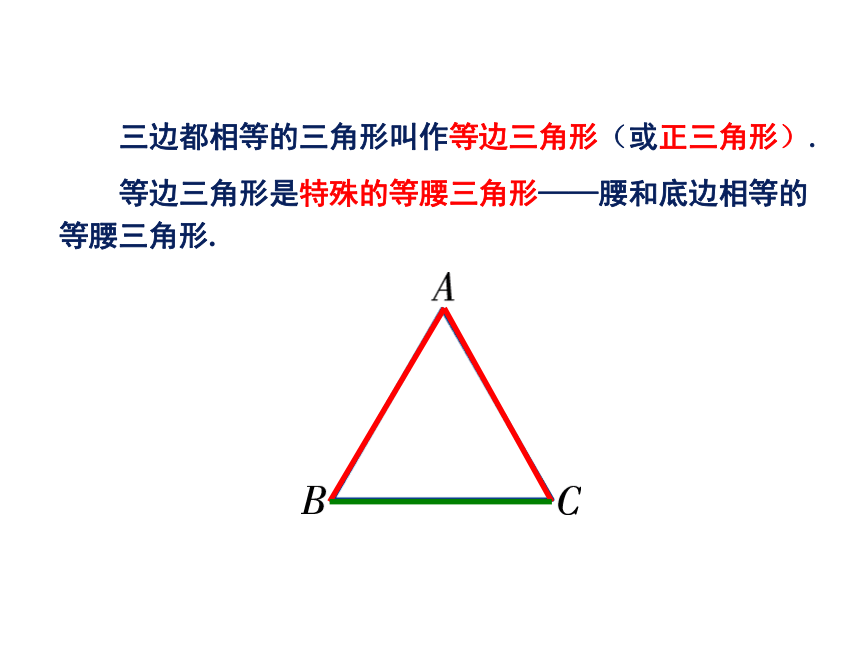
可分别用a,b,c来表示. 三角形中,有的三边各不相等,有的两边相等,有的三边都相等. 两条边相等的三角形叫作等腰三角形. 在等腰三角形中,相等的两边叫作腰, 另外一边叫作底边, 两腰的夹角叫作顶角, 腰和底边的夹角叫作底角.底边 三边都相等的三角形叫作等边三角形(或正三角形). 等边三角形是特殊的等腰三角形——腰和底边相等的等腰三角形.如果是任意长度的三根小木棒它们一定能拼成三角形吗?为什么有的拼不成三角形?试量一量它们的长度,你发现了什么?我们知道,“两点之间,线段最短”,因此在图中,有:由此可见,三角形三边之间有如下关系:用三根小木棒看能否拼成一个三角形.ABC三角形任意两边之和大于第三边.
三角形任意两边之差小于第三边.不一定不一定 只要满足较小的两条线段之和大于第三条线段,便可构成三角形;若不满足,则不能构成三角形.两短边之和大于长边.两边之差<第三边<两边之和(1)5cm,8cm,2cm (2)3㎝,3㎝,4㎝解:(1)因为5 + 2 = 7< 8,不满足两边之和大于第三边,所以不能摆成三角形.(2)最长线段为4cm,因为3 + 3 = 6>4,满足两边之和大于第三边,所以能摆成三角形.友情提醒:只需比较两较短线段之和与最长线段的大小(3)因为5 + 8= 13=13,不满足两边之和大于第三边,所以不能摆成三角形.(4)最长线段为7.5cm,因为3.5 + 4.5 =8>7.5,满足两边之和大于第三边,所以能摆成三角形.(3)5cm,8cm,13cm (4)3.5㎝,7.5㎝,4.5㎝例2 下面分别是三根小木棒的长度,用它们能摆成三角形吗?只要满足较小的两条线段之和大于第三条线段,便可构成三角形;若不满足,则不能构成三角形.下列长度的各组线段能否组成一个三角形,并说明理由?
(1)15cm、10cm、7cm (2) 4cm、5cm、10cm
(3) 3cm、8cm、5cm (4) 4cm、5cm、6cm练一练4.一个等腰三角形的一边长9cm,另一边长4cm,则它的周长是多少?为什么?
提示:既然是等腰三角形,那么另一边的长要么是4, 要么是9cm.
如果是4cm,那么4 ﹢ 4﹤9cm,这样不满足三角形的三边关系,所以另一边的长只能是9cm,周长就应该是9﹢9﹢4=22cm.
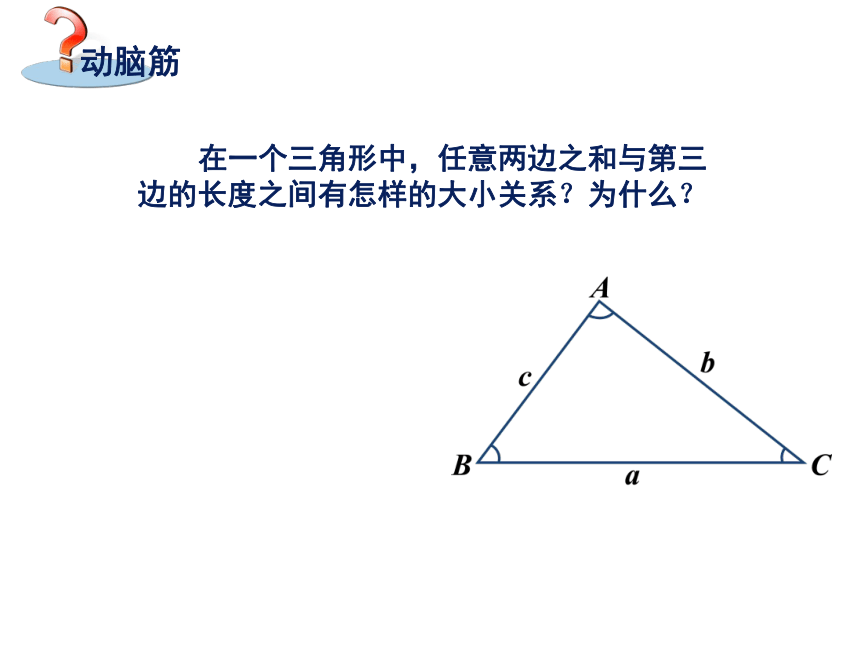
3.一个三角形的两边长分别是2cm、5cm,则第三边长X的取值范围是多少? 分析: X应满足大于5﹣2﹦3cm,小于5 ﹢ 2 ﹦7cm,所以3﹤X﹤7. 在一个三角形中,任意两边之和与第三边的长度之间有怎样的大小关系?为什么? 在△ABC中,BC是连接B,C两点的一条线段,由基本事实“两点之间线段最短”可得 AB + AC > BC.同理可得AB + BC > AC,AC + BC > AB .三角形的任意两边之和大于第三边.一般地,我们可以得出:两短边之和大于长边.
有三根木棒,其长度分别为2cm,3cm,6cm,它们能否首尾相接构成一个三角形?举
例例1 如图,D是△ABC的边AC上一点,AD=BD,
试判断AC与BC的大小.解 在△BDC 中,有 BD+DC >BC(三角形的任意两边之和大于第三边).又 AD = BD,则 BD+DC = AD+DC = AC,所以 AC >BC.1.(1)如图,图中有几个三角形?把它们分别
表示出来.答:五个三角形.(2)如图,在△DBC 中,写出∠D 的对边,
BD 边的对角.答:∠D的对边是BC,
BD边的对角是∠BCD.2. 三根长分别为2cm,5cm,6cm的小木棒能
首尾相接构成一个三角形吗?答:能. 从三角形的一个顶点向它的对边所在的直线作垂线,顶点和垂足之间的线段叫作三角形的高线,简称三角形的高. 如图,AH⊥BC,垂足为点H,则线段AH是△ABC的BC边上的高.如图,试画出图中△ABC的BC边上的高.D 在三角形中,一个角的平分线与这个角的对边相交,这个角的顶点与交点之间的线段叫作三角形的角平分线. 如图,∠BAD=∠CAD,则线段AD是△ABC的一条角平分线. 在三角形中,连接一个顶点和它的对边中点的线段叫作三角形的中线. 如图,BE=EC,则线段AE是△ABC的BC边上的中线. 任意画一个三角形,画出三边上的中线.你发现了什么?EFDEFD 事实上,三角形的三条中线相交于一点. 我们把这三条中线的交点叫作三角形的重心. 如图,△ABC的三条中线AD,BE,CF相交于点G,则点G为△ABC的重心.G举
例例2 如图,AD是△ABC的中线,AE是△ABC的高.
(1)图中共有几个三角形?请分别列举出来.解 (1)图中有6个三角形,它们分别是:△ABD,△ADE,△AEC,△ABE,△ADC,△ABC.(2)其中哪些三角形的面积相等?解 因为AD是△ABC的中线,所以 BD=DC.因为AE是△ABC的高,也是△ABD和△ADC的高,所以S△ABD = S△ADC .又1. 利用三角尺(或直尺)、量角器任意画出一
个三角形,并画出其中一条边上的中线、高以
及这条边所对的角的平分线.2. 如图,AD是△ABC的高,DE是△ADB的中线,
BF是△EBD的角平分线,根据已知条件填空:ADC90AEABEBFDBE 在小学,我们通过对一个三角形进行折叠、剪拼等操作(如图),知道三角形的内角和是180°,你能说出这些方法的原理吗? 在小学,我们通过对一个三角形进行折叠、剪拼等操作(如图),知道三角形的内角和是180°,你能说出这些方法的原理吗? 上述两种操作都是将三角形的三个内角拼到一起构成一个平角.由此受到启发:因为直线在平移下的像是与它平行的直线,如图,将△ABC的边BC所在的直线平移,
使其像经过点A,得到直线 .所以 .则 ,所以∠B+∠BAC+∠C=180°.又三角形的内角和等于180°.举
例例3 在△ABC中,∠A的度数是∠B的度数的3倍,
∠C 比∠B 大15°,求∠A,∠B,∠C的度数.解 设∠B为x °,则∠A为(3x)°,∠C为(x+ 15)°,从而有 3x+x+(x+15)=180.解得 x=33.所以 3x=99 ,x+15 =48.答:∠A,∠B,∠C的度数分别
为99°,33°,48°. 一个三角形的三个内角中,最多有几个直角?最多有几个钝角? 三角形的内角和等于180°,因此最多有一个直角或一个钝角. 三角形中,三个角都是锐角的三角形叫锐角三角形, 有一个角是直角的三角形叫直角三角形,有一个角是钝角的三角形叫钝角三角形.锐角三角形直角三角形钝角三角形 直角三角形可用符号“Rt△”来表示,例如直角三角形ABC可以记作“Rt△ABC”. 在直角三角形中,夹直角的两边叫作直角边,直角的对边叫作斜边. 两条直角边相等的直角三角形叫作等腰直角三角形. 如图,把△ABC的一边BC延长,得到∠ACD. 像这样,三角形的一边与另一边的延长线所组成的角,叫作三角形的外角. 对外角∠ACD来说,∠ACB是与它相邻的内角,∠A,∠B是与它不相邻的内角. 在图中,外角∠ACD和与它不相邻的内角∠A,∠B之间有什么大小关系? 我觉得可以利用“三角形的内角和等于180°”的结论.因为∠ACD+∠ACB = 180°,
∠A +∠B +∠ACB = 180°,所以∠ACD -∠A -∠B = 0(等量减等量,差相等)于是∠ACD =∠A +∠B. 三角形的一个外角等于与它不相邻的两个内角的和.1. 填空:
(1)在△ABC中,∠A= 60°,∠B=∠C,
则∠B= ;(2)在△ABC中,∠A-∠B= 50°,
∠C-∠B= 40°, 则∠B= .60°30°2. 如图,AD是△ABC的角平分线,∠B= 36°,
∠C= 76°,求∠DAC的度数.答:∠DAC的度数是34°3. 如图,∠CAD=100°,∠B=30°,
求∠C 的度数.答:∠C的度数是70°
可分别用a,b,c来表示. 三角形中,有的三边各不相等,有的两边相等,有的三边都相等. 两条边相等的三角形叫作等腰三角形. 在等腰三角形中,相等的两边叫作腰, 另外一边叫作底边, 两腰的夹角叫作顶角, 腰和底边的夹角叫作底角.底边 三边都相等的三角形叫作等边三角形(或正三角形). 等边三角形是特殊的等腰三角形——腰和底边相等的等腰三角形.如果是任意长度的三根小木棒它们一定能拼成三角形吗?为什么有的拼不成三角形?试量一量它们的长度,你发现了什么?我们知道,“两点之间,线段最短”,因此在图中,有:由此可见,三角形三边之间有如下关系:用三根小木棒看能否拼成一个三角形.ABC三角形任意两边之和大于第三边.
三角形任意两边之差小于第三边.不一定不一定 只要满足较小的两条线段之和大于第三条线段,便可构成三角形;若不满足,则不能构成三角形.两短边之和大于长边.两边之差<第三边<两边之和(1)5cm,8cm,2cm (2)3㎝,3㎝,4㎝解:(1)因为5 + 2 = 7< 8,不满足两边之和大于第三边,所以不能摆成三角形.(2)最长线段为4cm,因为3 + 3 = 6>4,满足两边之和大于第三边,所以能摆成三角形.友情提醒:只需比较两较短线段之和与最长线段的大小(3)因为5 + 8= 13=13,不满足两边之和大于第三边,所以不能摆成三角形.(4)最长线段为7.5cm,因为3.5 + 4.5 =8>7.5,满足两边之和大于第三边,所以能摆成三角形.(3)5cm,8cm,13cm (4)3.5㎝,7.5㎝,4.5㎝例2 下面分别是三根小木棒的长度,用它们能摆成三角形吗?只要满足较小的两条线段之和大于第三条线段,便可构成三角形;若不满足,则不能构成三角形.下列长度的各组线段能否组成一个三角形,并说明理由?
(1)15cm、10cm、7cm (2) 4cm、5cm、10cm
(3) 3cm、8cm、5cm (4) 4cm、5cm、6cm练一练4.一个等腰三角形的一边长9cm,另一边长4cm,则它的周长是多少?为什么?
提示:既然是等腰三角形,那么另一边的长要么是4, 要么是9cm.
如果是4cm,那么4 ﹢ 4﹤9cm,这样不满足三角形的三边关系,所以另一边的长只能是9cm,周长就应该是9﹢9﹢4=22cm.
3.一个三角形的两边长分别是2cm、5cm,则第三边长X的取值范围是多少? 分析: X应满足大于5﹣2﹦3cm,小于5 ﹢ 2 ﹦7cm,所以3﹤X﹤7. 在一个三角形中,任意两边之和与第三边的长度之间有怎样的大小关系?为什么? 在△ABC中,BC是连接B,C两点的一条线段,由基本事实“两点之间线段最短”可得 AB + AC > BC.同理可得AB + BC > AC,AC + BC > AB .三角形的任意两边之和大于第三边.一般地,我们可以得出:两短边之和大于长边.
有三根木棒,其长度分别为2cm,3cm,6cm,它们能否首尾相接构成一个三角形?举
例例1 如图,D是△ABC的边AC上一点,AD=BD,
试判断AC与BC的大小.解 在△BDC 中,有 BD+DC >BC(三角形的任意两边之和大于第三边).又 AD = BD,则 BD+DC = AD+DC = AC,所以 AC >BC.1.(1)如图,图中有几个三角形?把它们分别
表示出来.答:五个三角形.(2)如图,在△DBC 中,写出∠D 的对边,
BD 边的对角.答:∠D的对边是BC,
BD边的对角是∠BCD.2. 三根长分别为2cm,5cm,6cm的小木棒能
首尾相接构成一个三角形吗?答:能. 从三角形的一个顶点向它的对边所在的直线作垂线,顶点和垂足之间的线段叫作三角形的高线,简称三角形的高. 如图,AH⊥BC,垂足为点H,则线段AH是△ABC的BC边上的高.如图,试画出图中△ABC的BC边上的高.D 在三角形中,一个角的平分线与这个角的对边相交,这个角的顶点与交点之间的线段叫作三角形的角平分线. 如图,∠BAD=∠CAD,则线段AD是△ABC的一条角平分线. 在三角形中,连接一个顶点和它的对边中点的线段叫作三角形的中线. 如图,BE=EC,则线段AE是△ABC的BC边上的中线. 任意画一个三角形,画出三边上的中线.你发现了什么?EFDEFD 事实上,三角形的三条中线相交于一点. 我们把这三条中线的交点叫作三角形的重心. 如图,△ABC的三条中线AD,BE,CF相交于点G,则点G为△ABC的重心.G举
例例2 如图,AD是△ABC的中线,AE是△ABC的高.
(1)图中共有几个三角形?请分别列举出来.解 (1)图中有6个三角形,它们分别是:△ABD,△ADE,△AEC,△ABE,△ADC,△ABC.(2)其中哪些三角形的面积相等?解 因为AD是△ABC的中线,所以 BD=DC.因为AE是△ABC的高,也是△ABD和△ADC的高,所以S△ABD = S△ADC .又1. 利用三角尺(或直尺)、量角器任意画出一
个三角形,并画出其中一条边上的中线、高以
及这条边所对的角的平分线.2. 如图,AD是△ABC的高,DE是△ADB的中线,
BF是△EBD的角平分线,根据已知条件填空:ADC90AEABEBFDBE 在小学,我们通过对一个三角形进行折叠、剪拼等操作(如图),知道三角形的内角和是180°,你能说出这些方法的原理吗? 在小学,我们通过对一个三角形进行折叠、剪拼等操作(如图),知道三角形的内角和是180°,你能说出这些方法的原理吗? 上述两种操作都是将三角形的三个内角拼到一起构成一个平角.由此受到启发:因为直线在平移下的像是与它平行的直线,如图,将△ABC的边BC所在的直线平移,
使其像经过点A,得到直线 .所以 .则 ,所以∠B+∠BAC+∠C=180°.又三角形的内角和等于180°.举
例例3 在△ABC中,∠A的度数是∠B的度数的3倍,
∠C 比∠B 大15°,求∠A,∠B,∠C的度数.解 设∠B为x °,则∠A为(3x)°,∠C为(x+ 15)°,从而有 3x+x+(x+15)=180.解得 x=33.所以 3x=99 ,x+15 =48.答:∠A,∠B,∠C的度数分别
为99°,33°,48°. 一个三角形的三个内角中,最多有几个直角?最多有几个钝角? 三角形的内角和等于180°,因此最多有一个直角或一个钝角. 三角形中,三个角都是锐角的三角形叫锐角三角形, 有一个角是直角的三角形叫直角三角形,有一个角是钝角的三角形叫钝角三角形.锐角三角形直角三角形钝角三角形 直角三角形可用符号“Rt△”来表示,例如直角三角形ABC可以记作“Rt△ABC”. 在直角三角形中,夹直角的两边叫作直角边,直角的对边叫作斜边. 两条直角边相等的直角三角形叫作等腰直角三角形. 如图,把△ABC的一边BC延长,得到∠ACD. 像这样,三角形的一边与另一边的延长线所组成的角,叫作三角形的外角. 对外角∠ACD来说,∠ACB是与它相邻的内角,∠A,∠B是与它不相邻的内角. 在图中,外角∠ACD和与它不相邻的内角∠A,∠B之间有什么大小关系? 我觉得可以利用“三角形的内角和等于180°”的结论.因为∠ACD+∠ACB = 180°,
∠A +∠B +∠ACB = 180°,所以∠ACD -∠A -∠B = 0(等量减等量,差相等)于是∠ACD =∠A +∠B. 三角形的一个外角等于与它不相邻的两个内角的和.1. 填空:
(1)在△ABC中,∠A= 60°,∠B=∠C,
则∠B= ;(2)在△ABC中,∠A-∠B= 50°,
∠C-∠B= 40°, 则∠B= .60°30°2. 如图,AD是△ABC的角平分线,∠B= 36°,
∠C= 76°,求∠DAC的度数.答:∠DAC的度数是34°3. 如图,∠CAD=100°,∠B=30°,
求∠C 的度数.答:∠C的度数是70°
同课章节目录
