1.2.2 配方法(2)(湖南省邵阳市新邵县)
文档属性
| 名称 | 1.2.2 配方法(2)(湖南省邵阳市新邵县) |

|
|
| 格式 | rar | ||
| 文件大小 | 115.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-05-14 15:31:00 | ||
图片预览

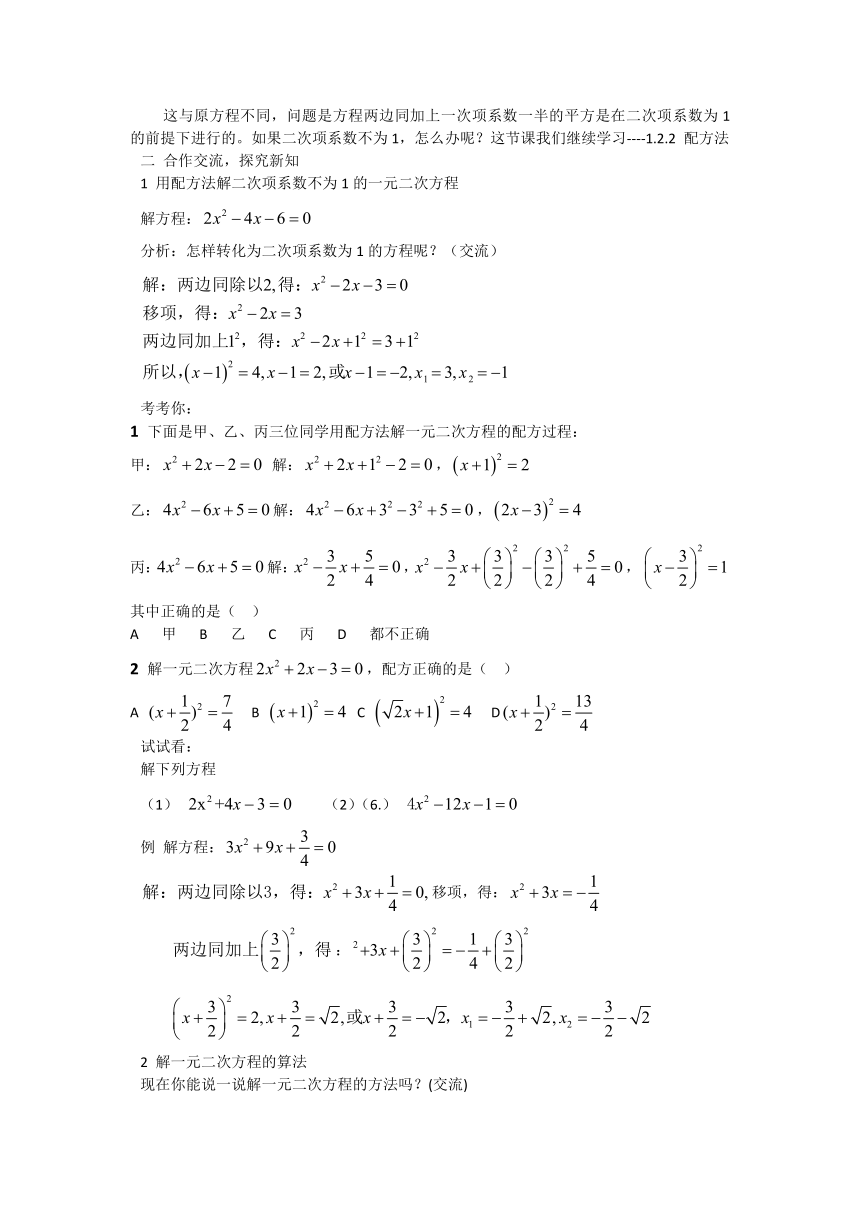
文档简介
课题 1.2.2 配方法
湖南省新邵县酿溪中学王军旗
教学目标
1 进一步理解用配方法解一元二次方程的步骤。
2 能熟练地运用配方法解二次项系数不是1的一元二次方程。
3 在学习运用配方法解二元一次方程的过程中使学生理解配方是一种常用的数学方法,增加对一元二次方程的感性认识。
4在通过探索用配方法将一元二次方程变形的过程中使学生积极参与学习活动,增进对方程的认识,进一步体会化归思想。
重点、难点
重点:会用配方法解二次项系数不为1的一元二次方程
难点:配方
教学过程
一 创设情境,导入新课
1 解方程:
,,
,
上面方程配方为:后,除了用直接开平方法解外,还有什么方法呢?
当一元二次方程的二次项系数为1时,解题步骤是:移----配-----解
2 观察下面解方程的过程,是否正确?
解方程:
解:
分析:把方程展开:
这与原方程不同,问题是方程两边同加上一次项系数一半的平方是在二次项系数为1的前提下进行的。如果二次项系数不为1,怎么办呢?这节课我们继续学习----1.2.2 配方法
二 合作交流,探究新知
1 用配方法解二次项系数不为1的一元二次方程
解方程:
分析:怎样转化为二次项系数为1的方程呢?(交流)
考考你:
1 下面是甲、乙、丙三位同学用配方法解一元二次方程的配方过程:
甲: 解:,
乙:解:,
丙:解:,,
其中正确的是( )
A 甲 B 乙 C 丙 D 都不正确
2 解一元二次方程,配方正确的是( )
A B C D
试试看:
解下列方程
(1) (2)(6.)
例 解方程:
移项,得:
:
2 解一元二次方程的算法
现在你能说一说解一元二次方程的方法吗?(交流)
教师归纳:解一元二次方程时,首先考虑是否能用直接开平方法和因式分解法,如果不能,就考虑用配方法,先化为的形式,然后两边同除以二次项系数,化为的形式,再移项配方。
练一练
解方程:(1),(2),(3)
三应用迁移,巩固提高
例1 一小球以15m/s的初速度竖直向上弹出,它在空中的高度h(m)与时间t(s)满足关系: h=15t-5t2 . 小球何时能达到10m的高度
,
, ,
例2代数式4+8x+5有最大值还是有最少值?是多少
解:设y=4+8x+5=
=≥1
所以,4+8x+5最小值为1.
四课堂练习,巩固提高
解下列方程
(1)(2x+1)(x-3)=1 (2) (3)
五反思小结,拓展提高
用配方法解二次项系数不是1的一元二次方程的步骤:
1.化1:把二次项系数化为1(方程两边都除以二次项系数);
2.移项:把常数项移到方程的右边;
3.配方:方程两边都加上一次项系数绝对值一半的平方;
4.变形:方程左分解因式,右边合并同类;
5.开方:根据平方根意义,方程两边开平方;
6.求解:解一元一次方程;
7.定解:写出原方程的解.
作业
1解下列方程:
(1).6x2 -7x+ 1 = 0; (2).5x2 -9x –18=0; (3).4x 2 –3x =52; (4). 5x2 =4-2x.
2一名跳水运动员进行10米跳台跳水训练,在正常情况下,运动员必须在距离水面5m以前完成规定的翻滚动作,并且调整好如水姿势,否则就容易出现失误,假设运动员起跳后,运动时间t(s)和运动员距离水面的高度h(m)满足关系:h=10+2.5t-5,那么他最多有多长时间完成规定动作?(精确到0.1s)
3如图,在△ABC中,∠B=90°,AB=5cm,BC=7cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC向点C以2cm/s的速度移动,如果P、Q分别从A,B同时出发那么几秒后△PBQ的面积等于4 ,
湖南省新邵县酿溪中学王军旗
教学目标
1 进一步理解用配方法解一元二次方程的步骤。
2 能熟练地运用配方法解二次项系数不是1的一元二次方程。
3 在学习运用配方法解二元一次方程的过程中使学生理解配方是一种常用的数学方法,增加对一元二次方程的感性认识。
4在通过探索用配方法将一元二次方程变形的过程中使学生积极参与学习活动,增进对方程的认识,进一步体会化归思想。
重点、难点
重点:会用配方法解二次项系数不为1的一元二次方程
难点:配方
教学过程
一 创设情境,导入新课
1 解方程:
,,
,
上面方程配方为:后,除了用直接开平方法解外,还有什么方法呢?
当一元二次方程的二次项系数为1时,解题步骤是:移----配-----解
2 观察下面解方程的过程,是否正确?
解方程:
解:
分析:把方程展开:
这与原方程不同,问题是方程两边同加上一次项系数一半的平方是在二次项系数为1的前提下进行的。如果二次项系数不为1,怎么办呢?这节课我们继续学习----1.2.2 配方法
二 合作交流,探究新知
1 用配方法解二次项系数不为1的一元二次方程
解方程:
分析:怎样转化为二次项系数为1的方程呢?(交流)
考考你:
1 下面是甲、乙、丙三位同学用配方法解一元二次方程的配方过程:
甲: 解:,
乙:解:,
丙:解:,,
其中正确的是( )
A 甲 B 乙 C 丙 D 都不正确
2 解一元二次方程,配方正确的是( )
A B C D
试试看:
解下列方程
(1) (2)(6.)
例 解方程:
移项,得:
:
2 解一元二次方程的算法
现在你能说一说解一元二次方程的方法吗?(交流)
教师归纳:解一元二次方程时,首先考虑是否能用直接开平方法和因式分解法,如果不能,就考虑用配方法,先化为的形式,然后两边同除以二次项系数,化为的形式,再移项配方。
练一练
解方程:(1),(2),(3)
三应用迁移,巩固提高
例1 一小球以15m/s的初速度竖直向上弹出,它在空中的高度h(m)与时间t(s)满足关系: h=15t-5t2 . 小球何时能达到10m的高度
,
, ,
例2代数式4+8x+5有最大值还是有最少值?是多少
解:设y=4+8x+5=
=≥1
所以,4+8x+5最小值为1.
四课堂练习,巩固提高
解下列方程
(1)(2x+1)(x-3)=1 (2) (3)
五反思小结,拓展提高
用配方法解二次项系数不是1的一元二次方程的步骤:
1.化1:把二次项系数化为1(方程两边都除以二次项系数);
2.移项:把常数项移到方程的右边;
3.配方:方程两边都加上一次项系数绝对值一半的平方;
4.变形:方程左分解因式,右边合并同类;
5.开方:根据平方根意义,方程两边开平方;
6.求解:解一元一次方程;
7.定解:写出原方程的解.
作业
1解下列方程:
(1).6x2 -7x+ 1 = 0; (2).5x2 -9x –18=0; (3).4x 2 –3x =52; (4). 5x2 =4-2x.
2一名跳水运动员进行10米跳台跳水训练,在正常情况下,运动员必须在距离水面5m以前完成规定的翻滚动作,并且调整好如水姿势,否则就容易出现失误,假设运动员起跳后,运动时间t(s)和运动员距离水面的高度h(m)满足关系:h=10+2.5t-5,那么他最多有多长时间完成规定动作?(精确到0.1s)
3如图,在△ABC中,∠B=90°,AB=5cm,BC=7cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC向点C以2cm/s的速度移动,如果P、Q分别从A,B同时出发那么几秒后△PBQ的面积等于4 ,
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
