江苏省泰州中学附属初级中学2023-2024学年九年级下学期数学第一次月考模拟试题(含答案)
文档属性
| 名称 | 江苏省泰州中学附属初级中学2023-2024学年九年级下学期数学第一次月考模拟试题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-23 09:24:27 | ||
图片预览



文档简介
九年级(上)第一次月考数学模拟试卷2024.3.19
第Ⅰ卷(选择题)
一、选择题:本题共6小题,每小题3分,共18分.在每小题给出的选项中,只有一项是符合题目要求的.
1.将一个棱长为4的正方体的表面涂成灰色,再把它分割成棱长为1的小正方体,从中任取一个小正方体,则取得的小正方体恰有三个面涂有灰色的概率为( )
A. B. C. D.
2.甲、乙、丙、丁四人10次随堂测验的成绩如图所示,从图中可以看出这10次测验平均成绩较高且较稳定是( )
A.甲 B.乙 C.丙 D.丁
3.为迎接中国共产党建党一百周年,某班50名同学进行了党史知识竞赛,测试成绩统计如下表,其中有两个数据被遮盖.
成绩/分 91 92 93 94 95 96 97 98 99 100
人数 ■ ■ 1 2 3 5 6 8 10 12
下列关于成绩的统计量中,与被遮盖的数据无关的是( )
A.平均数,方差 B.中位数,方差 C.中位数,众数 D.平均数,众数
4.一个扇形的弧长是,面积是,则此扇形的圆心角的度数是( )
A. B. C. D.
5.若关于的方程没有实数根,则的值可以是( )
A. B. C.0 D.1
6.下列关于圆的说法中,正确的是( )
A.过三点可以作一个圆 B.相等的圆心角所对的弧相等
C.平分弦的直径垂直于弦 D.圆的直径所在的直线是它的对称轴
第Ⅱ卷(非选择题)
二、填空题:本题共10小题,每小题3分,共30分.
7.,且都是集合的子集,若把叫做集合的“长度”,则集合的长度的最小值是_______.
8.如图,一个正边形纸片被撕掉了一部分,已知它的中心角是,那么_______.
9.一只蚂蚁在如图所示的正方形地砖上爬行,蚂蚁停在阴影部分的概率为_______.
10.某校组织学生参加植树活动,活动结束后,统计了九年级甲班50名学生每人植树的情况,绘制了如下的统计表:
植树棵数 3 4 5 6
人数 20 15 10 5
那么这50名学生平均每人植树_______棵.
11.设是关于的方程的两个根,且,则_______.
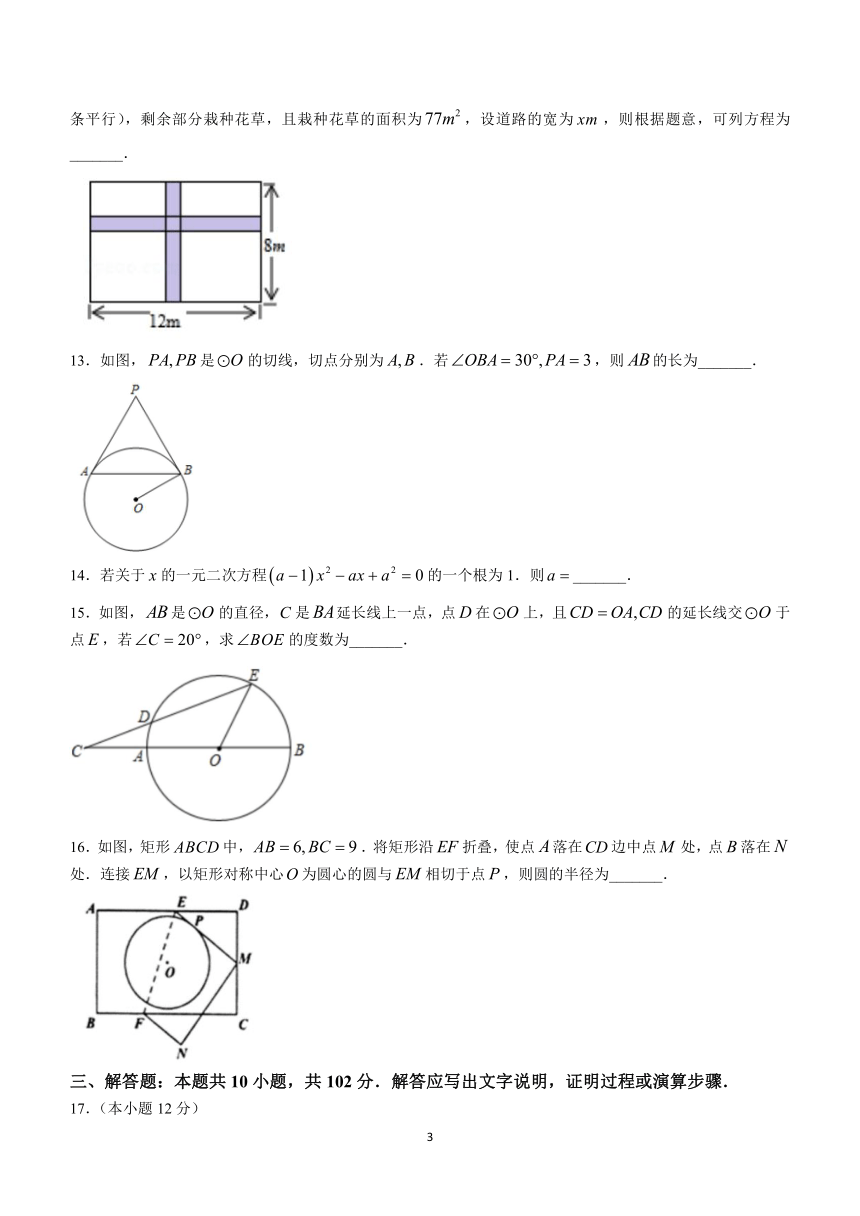
12.如图,在一块长,宽的矩形空地上,修建同样宽的两条互相垂直的道路(两条道路各与矩形的一条平行),剩余部分栽种花草,且栽种花草的面积为,设道路的宽为,则根据题意,可列方程为_______.
13.如图,是的切线,切点分别为.若,则的长为_______.
14.若关于的一元二次方程的一个根为1.则_______.
15.如图,是的直径,是延长线上一点,点在上,且的延长线交于点,若,求的度数为_______.
16.如图,矩形中,.将矩形沿折叠,使点落在边中点处,点落在处.连接,以矩形对称中心为圆心的圆与相切于点,则圆的半径为_______.
三、解答题:本题共10小题,共102分.解答应写出文字说明,证明过程或演算步骤.
17.(本小题12分)
用适当的方法解下列方程:
(1); (2);
(3); (4).
18.(本小题8分)
如图,是的直径,点在上,,垂足为分别交于点.
(1)求证:;
(2)若,求的长度.
19.(本小题8分)
嘉嘉与淇淇两位同学解方程的过程如下:
嘉嘉:两边同除以,得,则. 淇淇:移项,得,提取公因式,得.则或,解得.
(1)嘉嘉的解法_______;淇淇的解法_______;(填“正确”或“不正确”)
(2)请你选择合适的方法尝试解一元二次方程.
20.(本小题8分)
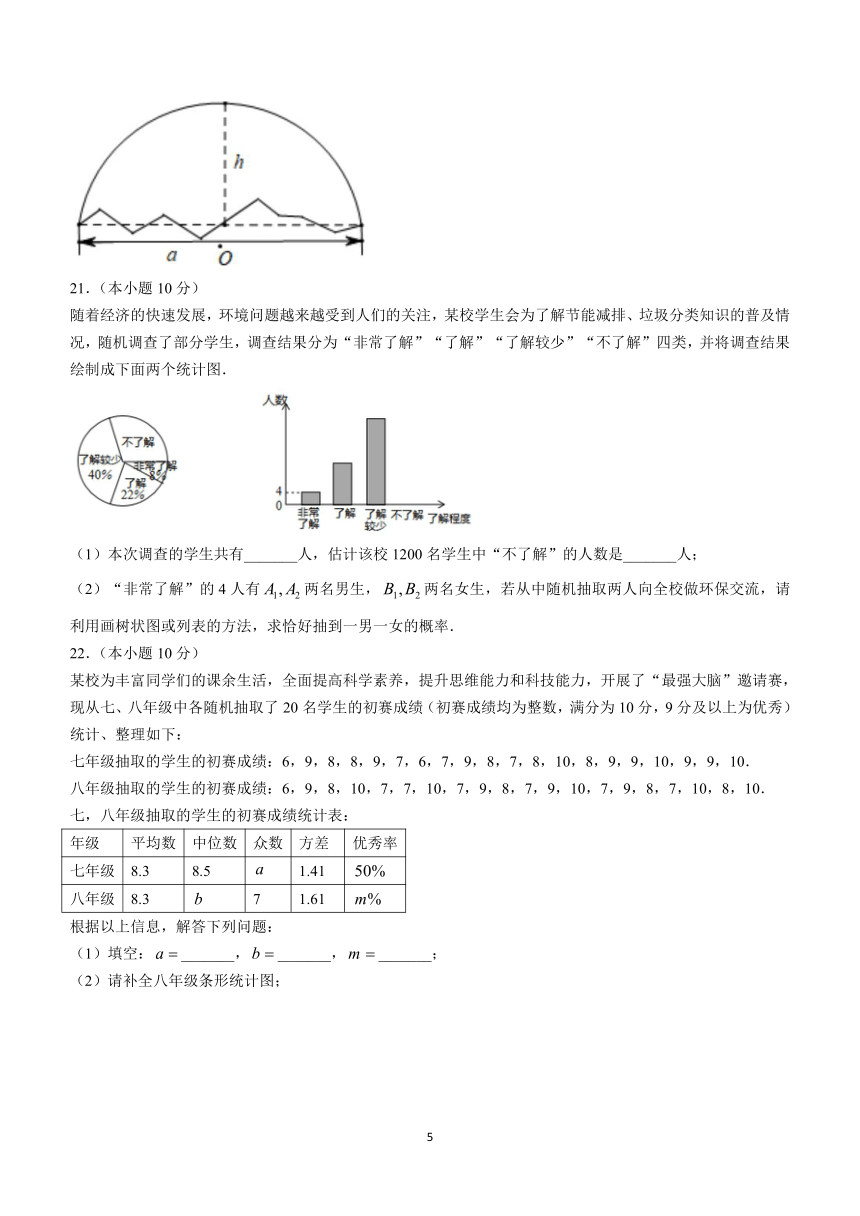
一个残破的车轮如图所示,测得它所剩圆孤两端点间的距离,弧的中点到弧所对弦的距离.如果需要加工与原来大小相同的车轮,那么这个车轮的半径是多少 (结果精确到)
21.(本小题10分)
随着经济的快速发展,环境问题越来越受到人们的关注,某校学生会为了解节能减排、垃圾分类知识的普及情况,随机调查了部分学生,调查结果分为“非常了解”“了解”“了解较少”“不了解”四类,并将调查结果绘制成下面两个统计图.
(1)本次调查的学生共有_______人,估计该校1200名学生中“不了解”的人数是_______人;
(2)“非常了解”的4人有两名男生,两名女生,若从中随机抽取两人向全校做环保交流,请利用画树状图或列表的方法,求恰好抽到一男一女的概率.
22.(本小题10分)
某校为丰富同学们的课余生活,全面提高科学素养,提升思维能力和科技能力,开展了“最强大脑”邀请赛,现从七、八年级中各随机抽取了20名学生的初赛成绩(初赛成绩均为整数,满分为10分,9分及以上为优秀)统计、整理如下:
七年级抽取的学生的初赛成绩:6,9,8,8,9,7,6,7,9,8,7,8,10,8,9,9,10,9,9,10.
八年级抽取的学生的初赛成绩:6,9,8,10,7,7,10,7,9,8,7,9,10,7,9,8,7,10,8,10.
七,八年级抽取的学生的初赛成绩统计表:
年级 平均数 中位数 众数 方差 优秀率
七年级 8.3 8.5 1.41
八年级 8.3 7 1.61
根据以上信息,解答下列问题:
(1)填空:_______,_______,_______;
(2)请补全八年级条形统计图;
(3)在本次“最强大脑”邀请赛中,_______年级的初赛成绩相对稳定;(选填“七”或“八”.)
(4)若七年级有学生800人,八年级有学生900人,且满分才能进入决赛,估计全校进入决赛的学生共有_______人.
23.(本小题10分)
已知关于的一元二次方程有两个实数根.
(1)求的取值范围;
(2)若,求的值.
24.(本小题10分)
如图,在中,,在上取一点,以为直径作,与相交于点,作线段的垂直平分线交于点,连接.
(1)求证:是的切线;
(2)若的半径为1,求线段的长.
25.(本小题12分)
某农户生产经销一种农产品,已知这种产品的成本价为每千克20元.市场调查发现,该产品每天的销售价为25(元/千克)时,每天销售量为30(千克).当产品的销售价每千克涨1元时每天销售量会减少2千克,设涨价(元/千克)(为正整数),每天销售量为(千克).
(1)求与之间的函数关系式.
(2)该农户想要每天获得128元的销售利润,销售价为多少
(3)每千克涨价多少元时,每天的销售利润最大 最大利润是多少元
26.(本小题14分)
如图①,已知是的外接圆,(为上一点,连接交于点.
图① 图② 图③
(1)连接,若,求的大小;
(2)如图②,若点恰好是中点,求证:;
(3)如图③,将分别沿翻折得到,连接,若为直径,请问是否为定值,如果是,请求出这个值,如果不是,请说明理由.
九年级(上)第一次月考数学模拟试卷答案2024.3.19
1.【答案】C 2.【答案】C 3.【答案】C 4.【答案】B 5.【答案】A 6.【答案】D
7.【答案】 8.【答案】9 9.【答案】 10.【答案】4 11.【答案】2
12.【答案】 13.【答案】3 14.【答案】 15.【答案】 16.【答案】2.7
17.【答案】解:(1),
,,即;
(2),,,
,;
(3),,
,
或,;
(4)方程化为,则,
,
该方程有两个不相等的根,且,
.
18.【答案】(1)证明:是的直径,,
,,,
,,,.
(2)解:如图,连接,
,
,,
是等边三角形,,
,,,
的长度.
19.【答案】不正确 正确
20.【答案】解:由垂径定理推论可得:,
设圆的半径为,则,
,即.
解得:.
答:这个车轮的半径为.
21.【答案】(1)50,360;
(2)画树状图,共有12种可能的结果,恰好抽到一男一女的结果有8个,
(恰好抽到一男一女的).
22.【答案】解:(1)9,8,45
(2)由题意可得:7分的人数为6人,10分的人数为5人
补全条形统计图:
(3)七
(4)345
23.【答案】解:
(1)方程有两个实数根,
解得;
(2)由根与系数的关系可得,
,,即,
,解得.
24.【答案】(1)证明:如图,连接,
,,
是的中垂线,,,
是直角三角形,,
,,
,
即,是半径,是的切线;
(2)解:如图,连接,
是的中垂线,,
设
在中,,
在中,,
,
即,
解得,即.
25.【答案】解:(1)由题意得
与之间的函数关系式为;
(2)由题意得
解得(不合题意,舍去),
则销售价位元,
答:销售价为36元;
(3)设每天的销售利润为元,
由题意得
,
则当时,最大为200元.
答:每千克涨价5元时,每天的销售利润最大,最大利润是200元.
26.【答案】解:(1),,
,
;
(2)证明:点是的中点,
,,,
,,
,,
,,;
(3)是定值.
方法一:将分别沿翻折得到,
,
,
过点作于点,则,
连接并延长交于点,连接,则,
图③
,,
在和中
,,
为定值.
方法二:连接,
图④
则,
,
,.
第Ⅰ卷(选择题)
一、选择题:本题共6小题,每小题3分,共18分.在每小题给出的选项中,只有一项是符合题目要求的.
1.将一个棱长为4的正方体的表面涂成灰色,再把它分割成棱长为1的小正方体,从中任取一个小正方体,则取得的小正方体恰有三个面涂有灰色的概率为( )
A. B. C. D.
2.甲、乙、丙、丁四人10次随堂测验的成绩如图所示,从图中可以看出这10次测验平均成绩较高且较稳定是( )
A.甲 B.乙 C.丙 D.丁
3.为迎接中国共产党建党一百周年,某班50名同学进行了党史知识竞赛,测试成绩统计如下表,其中有两个数据被遮盖.
成绩/分 91 92 93 94 95 96 97 98 99 100
人数 ■ ■ 1 2 3 5 6 8 10 12
下列关于成绩的统计量中,与被遮盖的数据无关的是( )
A.平均数,方差 B.中位数,方差 C.中位数,众数 D.平均数,众数
4.一个扇形的弧长是,面积是,则此扇形的圆心角的度数是( )
A. B. C. D.
5.若关于的方程没有实数根,则的值可以是( )
A. B. C.0 D.1
6.下列关于圆的说法中,正确的是( )
A.过三点可以作一个圆 B.相等的圆心角所对的弧相等
C.平分弦的直径垂直于弦 D.圆的直径所在的直线是它的对称轴
第Ⅱ卷(非选择题)
二、填空题:本题共10小题,每小题3分,共30分.
7.,且都是集合的子集,若把叫做集合的“长度”,则集合的长度的最小值是_______.
8.如图,一个正边形纸片被撕掉了一部分,已知它的中心角是,那么_______.
9.一只蚂蚁在如图所示的正方形地砖上爬行,蚂蚁停在阴影部分的概率为_______.
10.某校组织学生参加植树活动,活动结束后,统计了九年级甲班50名学生每人植树的情况,绘制了如下的统计表:
植树棵数 3 4 5 6
人数 20 15 10 5
那么这50名学生平均每人植树_______棵.
11.设是关于的方程的两个根,且,则_______.
12.如图,在一块长,宽的矩形空地上,修建同样宽的两条互相垂直的道路(两条道路各与矩形的一条平行),剩余部分栽种花草,且栽种花草的面积为,设道路的宽为,则根据题意,可列方程为_______.
13.如图,是的切线,切点分别为.若,则的长为_______.
14.若关于的一元二次方程的一个根为1.则_______.
15.如图,是的直径,是延长线上一点,点在上,且的延长线交于点,若,求的度数为_______.
16.如图,矩形中,.将矩形沿折叠,使点落在边中点处,点落在处.连接,以矩形对称中心为圆心的圆与相切于点,则圆的半径为_______.
三、解答题:本题共10小题,共102分.解答应写出文字说明,证明过程或演算步骤.
17.(本小题12分)
用适当的方法解下列方程:
(1); (2);
(3); (4).
18.(本小题8分)
如图,是的直径,点在上,,垂足为分别交于点.
(1)求证:;
(2)若,求的长度.
19.(本小题8分)
嘉嘉与淇淇两位同学解方程的过程如下:
嘉嘉:两边同除以,得,则. 淇淇:移项,得,提取公因式,得.则或,解得.
(1)嘉嘉的解法_______;淇淇的解法_______;(填“正确”或“不正确”)
(2)请你选择合适的方法尝试解一元二次方程.
20.(本小题8分)
一个残破的车轮如图所示,测得它所剩圆孤两端点间的距离,弧的中点到弧所对弦的距离.如果需要加工与原来大小相同的车轮,那么这个车轮的半径是多少 (结果精确到)
21.(本小题10分)
随着经济的快速发展,环境问题越来越受到人们的关注,某校学生会为了解节能减排、垃圾分类知识的普及情况,随机调查了部分学生,调查结果分为“非常了解”“了解”“了解较少”“不了解”四类,并将调查结果绘制成下面两个统计图.
(1)本次调查的学生共有_______人,估计该校1200名学生中“不了解”的人数是_______人;
(2)“非常了解”的4人有两名男生,两名女生,若从中随机抽取两人向全校做环保交流,请利用画树状图或列表的方法,求恰好抽到一男一女的概率.
22.(本小题10分)
某校为丰富同学们的课余生活,全面提高科学素养,提升思维能力和科技能力,开展了“最强大脑”邀请赛,现从七、八年级中各随机抽取了20名学生的初赛成绩(初赛成绩均为整数,满分为10分,9分及以上为优秀)统计、整理如下:
七年级抽取的学生的初赛成绩:6,9,8,8,9,7,6,7,9,8,7,8,10,8,9,9,10,9,9,10.
八年级抽取的学生的初赛成绩:6,9,8,10,7,7,10,7,9,8,7,9,10,7,9,8,7,10,8,10.
七,八年级抽取的学生的初赛成绩统计表:
年级 平均数 中位数 众数 方差 优秀率
七年级 8.3 8.5 1.41
八年级 8.3 7 1.61
根据以上信息,解答下列问题:
(1)填空:_______,_______,_______;
(2)请补全八年级条形统计图;
(3)在本次“最强大脑”邀请赛中,_______年级的初赛成绩相对稳定;(选填“七”或“八”.)
(4)若七年级有学生800人,八年级有学生900人,且满分才能进入决赛,估计全校进入决赛的学生共有_______人.
23.(本小题10分)
已知关于的一元二次方程有两个实数根.
(1)求的取值范围;
(2)若,求的值.
24.(本小题10分)
如图,在中,,在上取一点,以为直径作,与相交于点,作线段的垂直平分线交于点,连接.
(1)求证:是的切线;
(2)若的半径为1,求线段的长.
25.(本小题12分)
某农户生产经销一种农产品,已知这种产品的成本价为每千克20元.市场调查发现,该产品每天的销售价为25(元/千克)时,每天销售量为30(千克).当产品的销售价每千克涨1元时每天销售量会减少2千克,设涨价(元/千克)(为正整数),每天销售量为(千克).
(1)求与之间的函数关系式.
(2)该农户想要每天获得128元的销售利润,销售价为多少
(3)每千克涨价多少元时,每天的销售利润最大 最大利润是多少元
26.(本小题14分)
如图①,已知是的外接圆,(为上一点,连接交于点.
图① 图② 图③
(1)连接,若,求的大小;
(2)如图②,若点恰好是中点,求证:;
(3)如图③,将分别沿翻折得到,连接,若为直径,请问是否为定值,如果是,请求出这个值,如果不是,请说明理由.
九年级(上)第一次月考数学模拟试卷答案2024.3.19
1.【答案】C 2.【答案】C 3.【答案】C 4.【答案】B 5.【答案】A 6.【答案】D
7.【答案】 8.【答案】9 9.【答案】 10.【答案】4 11.【答案】2
12.【答案】 13.【答案】3 14.【答案】 15.【答案】 16.【答案】2.7
17.【答案】解:(1),
,,即;
(2),,,
,;
(3),,
,
或,;
(4)方程化为,则,
,
该方程有两个不相等的根,且,
.
18.【答案】(1)证明:是的直径,,
,,,
,,,.
(2)解:如图,连接,
,
,,
是等边三角形,,
,,,
的长度.
19.【答案】不正确 正确
20.【答案】解:由垂径定理推论可得:,
设圆的半径为,则,
,即.
解得:.
答:这个车轮的半径为.
21.【答案】(1)50,360;
(2)画树状图,共有12种可能的结果,恰好抽到一男一女的结果有8个,
(恰好抽到一男一女的).
22.【答案】解:(1)9,8,45
(2)由题意可得:7分的人数为6人,10分的人数为5人
补全条形统计图:
(3)七
(4)345
23.【答案】解:
(1)方程有两个实数根,
解得;
(2)由根与系数的关系可得,
,,即,
,解得.
24.【答案】(1)证明:如图,连接,
,,
是的中垂线,,,
是直角三角形,,
,,
,
即,是半径,是的切线;
(2)解:如图,连接,
是的中垂线,,
设
在中,,
在中,,
,
即,
解得,即.
25.【答案】解:(1)由题意得
与之间的函数关系式为;
(2)由题意得
解得(不合题意,舍去),
则销售价位元,
答:销售价为36元;
(3)设每天的销售利润为元,
由题意得
,
则当时,最大为200元.
答:每千克涨价5元时,每天的销售利润最大,最大利润是200元.
26.【答案】解:(1),,
,
;
(2)证明:点是的中点,
,,,
,,
,,
,,;
(3)是定值.
方法一:将分别沿翻折得到,
,
,
过点作于点,则,
连接并延长交于点,连接,则,
图③
,,
在和中
,,
为定值.
方法二:连接,
图④
则,
,
,.
同课章节目录
