人教版数学九年级下册28.2解直角三角形的应用 教学设计
文档属性
| 名称 | 人教版数学九年级下册28.2解直角三角形的应用 教学设计 |

|
|
| 格式 | docx | ||
| 文件大小 | 68.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-23 11:39:40 | ||
图片预览

文档简介
28.2解直角三角形的应用——坡度教学设计
一、教学目标
1.弄清铅垂高度、水平宽度、坡度(或坡比)、坡角等概念,
2.能应用解直角三角形的知识,解答综合的实际问题.并会解答相应的实际问题.
3.通过阅读教材、结合看图、讨论交流、例题学习来了解坡高、坡度、坡角及其关系,并获得解答应用题的一-些经验
4.通过本节课的学习一方面增强学生对解直角三角形的应用意识,另一方面培养学生耐心、细致、认真的学习态度.
二、教学重点:理解坡度和坡角的概念.
三、教学难点:利用坡度和坡角等条件,解决有关的实际问题
四、教学准备:课件
五、教学课时:1课时
六、教学过程:
【教学设计】鼓励学生思考,让学生初步知道坡角、坡度等在实际生活中的应用
探究一:(多媒体出示)概念引入1:坡度
(1)坡角:坡面与水平面的夹角
(2)坡度:坡面的垂直高度(h)和水平宽度(l)的比叫做坡度(或坡比)坡度一般写成i=1∶m的形式。坡度越大,则坡角越大,坡面就越陡。
坡度
【设计意图】引导学生通过自主探究,合作交流,使其对具体问题的认识从形象到抽象,训练学生能从实际问题中抽象出数学知识.旨在培养学生的问题意识;提高学生的抽象思维能力
探究二:课堂达标
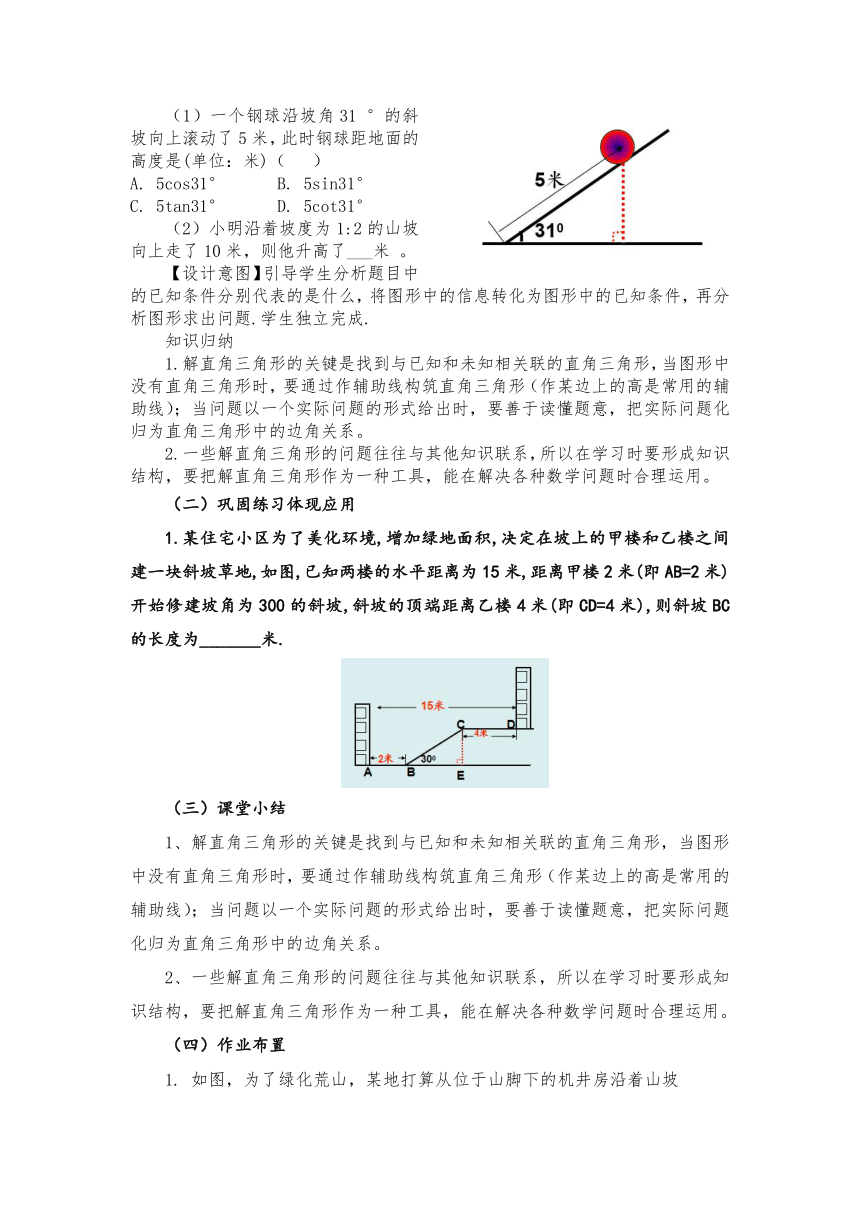
(1)一个钢球沿坡角31 °的斜坡向上滚动了5米,此时钢球距地面的高度是(单位:米)( )
A. 5cos31° B. 5sin31°
C. 5tan31° D. 5cot31°
(2)小明沿着坡度为1:2的山坡向上走了10米,则他升高了___米 。
【设计意图】引导学生分析题目中的已知条件分别代表的是什么,将图形中的信息转化为图形中的已知条件,再分析图形求出问题.学生独立完成.
知识归纳
1.解直角三角形的关键是找到与已知和未知相关联的直角三角形,当图形中没有直角三角形时,要通过作辅助线构筑直角三角形(作某边上的高是常用的辅助线);当问题以一个实际问题的形式给出时,要善于读懂题意,把实际问题化归为直角三角形中的边角关系。
2.一些解直角三角形的问题往往与其他知识联系,所以在学习时要形成知识结构,要把解直角三角形作为一种工具,能在解决各种数学问题时合理运用。
(二)巩固练习体现应用
1.某住宅小区为了美化环境,增加绿地面积,决定在坡上的甲楼和乙楼之间建一块斜坡草地,如图,已知两楼的水平距离为15米,距离甲楼2米(即AB=2米)开始修建坡角为300的斜坡,斜坡的顶端距离乙楼4米(即CD=4米),则斜坡BC的长度为_______米.
(三)课堂小结
1、解直角三角形的关键是找到与已知和未知相关联的直角三角形,当图形中没有直角三角形时,要通过作辅助线构筑直角三角形(作某边上的高是常用的辅助线);当问题以一个实际问题的形式给出时,要善于读懂题意,把实际问题化归为直角三角形中的边角关系。
2、一些解直角三角形的问题往往与其他知识联系,所以在学习时要形成知识结构,要把解直角三角形作为一种工具,能在解决各种数学问题时合理运用。
(四)作业布置
1. 如图,为了绿化荒山,某地打算从位于山脚下的机井房沿着山坡铺设水管,在山坡上修建一座扬水站,对坡面的绿地进行喷灌,现测得斜坡与水平面所成角的度数是30°,为使出水口的高度为35 m,那么需要准备的水管的长为( )
A. 17.5 m B. 35 m C. m D. 70 m
2. 如图,拦水坝的横断面为梯形ABCD,已知AD=5 m,DC=3 m,CE=4 m,CB的坡度i=1∶,则AB的长为 ( )
m B. 14 m C. m D. m
3.小明沿着坡度为1∶2的山坡向上走了1000 m,则他升高了( )
A. m B. 500 m C. m D. 1 000 m
4.某水坝的坡度i=1∶,坡长AB=20 m,则坝的高度为( )
A. 10 m B. 20 m C. 40m D. m
5.如图是一座人行天桥的示意图,天桥的高度是10米,,坡面AC的倾斜角为450,为了方便行人推车过天桥,市政部门决定降低坡度,使新坡面DC的玻度为i=:2,若新坡角下留3米宽的人行道,问离原坡角点处米的建筑物是否需要拆除?参考数据:,)
教学反思
虽然是网络授课,但仍然能通过课件和手写同时并用达到良好的授课效果,在本节课中用来源于学生比较熟悉的实际问题吸引他们的注意力,激发他们的好奇心,体会数学来源于生活并服务于生活,诱发学生对新知识的渴求。
解直角三角形的内容是初中阶段数学教学中重点之一,使学生对所学知识有了更好的巩固,同时让学生体会到数学与实际的联系.例题设置具有一定坡度,由浅入深,步步深入.逐步提高学生的思维能力
一、教学目标
1.弄清铅垂高度、水平宽度、坡度(或坡比)、坡角等概念,
2.能应用解直角三角形的知识,解答综合的实际问题.并会解答相应的实际问题.
3.通过阅读教材、结合看图、讨论交流、例题学习来了解坡高、坡度、坡角及其关系,并获得解答应用题的一-些经验
4.通过本节课的学习一方面增强学生对解直角三角形的应用意识,另一方面培养学生耐心、细致、认真的学习态度.
二、教学重点:理解坡度和坡角的概念.
三、教学难点:利用坡度和坡角等条件,解决有关的实际问题
四、教学准备:课件
五、教学课时:1课时
六、教学过程:
【教学设计】鼓励学生思考,让学生初步知道坡角、坡度等在实际生活中的应用
探究一:(多媒体出示)概念引入1:坡度
(1)坡角:坡面与水平面的夹角
(2)坡度:坡面的垂直高度(h)和水平宽度(l)的比叫做坡度(或坡比)坡度一般写成i=1∶m的形式。坡度越大,则坡角越大,坡面就越陡。
坡度
【设计意图】引导学生通过自主探究,合作交流,使其对具体问题的认识从形象到抽象,训练学生能从实际问题中抽象出数学知识.旨在培养学生的问题意识;提高学生的抽象思维能力
探究二:课堂达标
(1)一个钢球沿坡角31 °的斜坡向上滚动了5米,此时钢球距地面的高度是(单位:米)( )
A. 5cos31° B. 5sin31°
C. 5tan31° D. 5cot31°
(2)小明沿着坡度为1:2的山坡向上走了10米,则他升高了___米 。
【设计意图】引导学生分析题目中的已知条件分别代表的是什么,将图形中的信息转化为图形中的已知条件,再分析图形求出问题.学生独立完成.
知识归纳
1.解直角三角形的关键是找到与已知和未知相关联的直角三角形,当图形中没有直角三角形时,要通过作辅助线构筑直角三角形(作某边上的高是常用的辅助线);当问题以一个实际问题的形式给出时,要善于读懂题意,把实际问题化归为直角三角形中的边角关系。
2.一些解直角三角形的问题往往与其他知识联系,所以在学习时要形成知识结构,要把解直角三角形作为一种工具,能在解决各种数学问题时合理运用。
(二)巩固练习体现应用
1.某住宅小区为了美化环境,增加绿地面积,决定在坡上的甲楼和乙楼之间建一块斜坡草地,如图,已知两楼的水平距离为15米,距离甲楼2米(即AB=2米)开始修建坡角为300的斜坡,斜坡的顶端距离乙楼4米(即CD=4米),则斜坡BC的长度为_______米.
(三)课堂小结
1、解直角三角形的关键是找到与已知和未知相关联的直角三角形,当图形中没有直角三角形时,要通过作辅助线构筑直角三角形(作某边上的高是常用的辅助线);当问题以一个实际问题的形式给出时,要善于读懂题意,把实际问题化归为直角三角形中的边角关系。
2、一些解直角三角形的问题往往与其他知识联系,所以在学习时要形成知识结构,要把解直角三角形作为一种工具,能在解决各种数学问题时合理运用。
(四)作业布置
1. 如图,为了绿化荒山,某地打算从位于山脚下的机井房沿着山坡铺设水管,在山坡上修建一座扬水站,对坡面的绿地进行喷灌,现测得斜坡与水平面所成角的度数是30°,为使出水口的高度为35 m,那么需要准备的水管的长为( )
A. 17.5 m B. 35 m C. m D. 70 m
2. 如图,拦水坝的横断面为梯形ABCD,已知AD=5 m,DC=3 m,CE=4 m,CB的坡度i=1∶,则AB的长为 ( )
m B. 14 m C. m D. m
3.小明沿着坡度为1∶2的山坡向上走了1000 m,则他升高了( )
A. m B. 500 m C. m D. 1 000 m
4.某水坝的坡度i=1∶,坡长AB=20 m,则坝的高度为( )
A. 10 m B. 20 m C. 40m D. m
5.如图是一座人行天桥的示意图,天桥的高度是10米,,坡面AC的倾斜角为450,为了方便行人推车过天桥,市政部门决定降低坡度,使新坡面DC的玻度为i=:2,若新坡角下留3米宽的人行道,问离原坡角点处米的建筑物是否需要拆除?参考数据:,)
教学反思
虽然是网络授课,但仍然能通过课件和手写同时并用达到良好的授课效果,在本节课中用来源于学生比较熟悉的实际问题吸引他们的注意力,激发他们的好奇心,体会数学来源于生活并服务于生活,诱发学生对新知识的渴求。
解直角三角形的内容是初中阶段数学教学中重点之一,使学生对所学知识有了更好的巩固,同时让学生体会到数学与实际的联系.例题设置具有一定坡度,由浅入深,步步深入.逐步提高学生的思维能力
