数学人教A版(2019)选择性必修第三册7.3.1离散型随机变量的均值 课件(共28张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第三册7.3.1离散型随机变量的均值 课件(共28张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-22 00:00:00 | ||
图片预览







文档简介
(共28张PPT)
第七章 随机变量及其分布
7.3.1 离散型随机变量的均值
复习旧知
1、离散型随机变量的分布列
一般地,设离散型随机变量X的可能取值为x1,x2,…,xn,我们称X取每一个值xi的概率P(X=xi)=pi,i=1,2,…,n为X的概率分布列,简称分布列.
2、两点分布列
X 0 1
P 1-p p
复习旧知
3、数据的均值和方差
已知一组样本数据:x1,x2,…,xn
样本均值:
样本方差:
学习目标
1. 理解离散型随机变量均值的概念和含义,会根据离散型随机变量的分布列求出均值;
2. 掌握离散型随机变量的均值的性质和两点分布的均值;
3. 会利用离散型随机变量的均值反映离散型随机变量的取值水平,解决一些相关的实际问题.
4. 核心素养: 数据分析、逻辑推理、数学运算。
情境导学
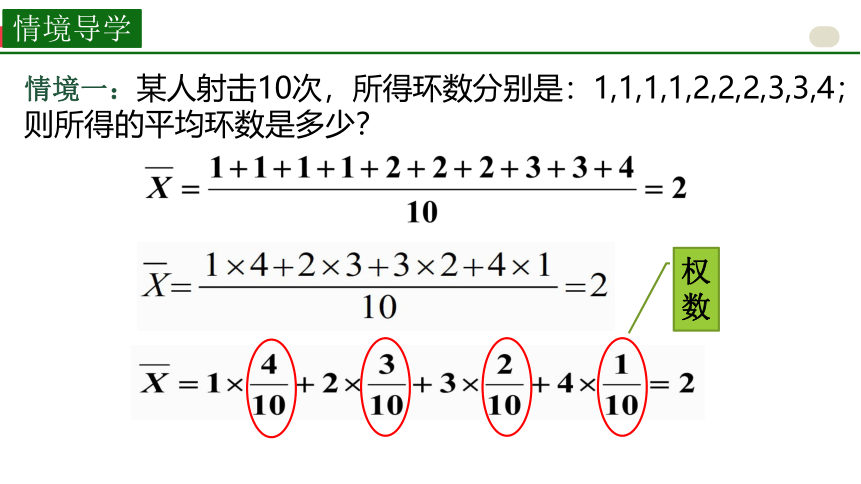
情境一:某人射击10次,所得环数分别是:1,1,1,1,2,2,2,3,3,4;则所得的平均环数是多少?
权数
情境导学
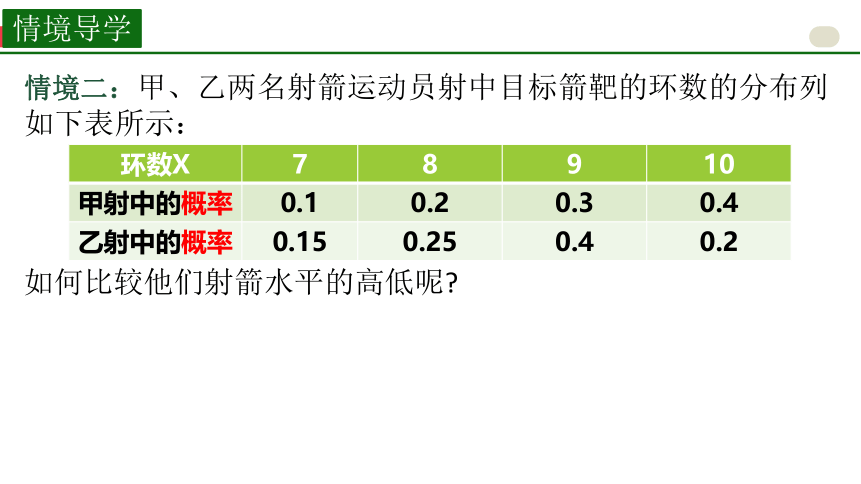
情境二:甲、乙两名射箭运动员射中目标箭靶的环数的分布列如下表所示:
环数X 7 8 9 10
甲射中的概率 0.1 0.2 0.3 0.4
乙射中的概率 0.15 0.25 0.4 0.2
如何比较他们射箭水平的高低呢
情境导学
假设甲射箭n次,射中7环、8环、9环和10环的频率分别为
甲n次射箭射中的平均环数为
当n足够大时,频率稳定于概率,所以 稳定于
即甲射中平均环数的稳定值为9,该值可以反映甲运动员的射箭水平.
所以,从平均值的角度比较,甲运动员的射箭水平比乙运动员高.
同理得乙射中环数的平均值:70.15+80.25+90.4+100.2=8.65.
情境导学
情境三:某商场要将单价分别为18元/kg,24元/kg,36元/kg的3种糖果按3:2:1的比例混合销售,如何对混合糖果定价才合理?
如果用X表示一颗糖果对应的单价,请写出随机变量X的分布列.
新知生成
一般地,若离散型随机变量X的分布列为:
离散型随机变量的均值(数学期望):
X x1 x2 ... xn
P p1 p2 ... pn
则称
1+2+...+
为随机变量X的均值或数学期望,简称期望. 它反映了离散型随机变量取值的平均水平.
典例剖析
例1 在篮球比赛中,罚球命中1次得1分,不中得0分. 如果某运动员罚球命中的概率为0.8,那么他罚球1次的得分X的均值是多少
解: 因为P(X=1)=0.8 , P(X=0)=0.2 ,
所以E(X)=0 × 0.2 + 1 × 0.8=0.8 .
即该运动员罚球1次的得分X的均值是0.8 .
思考:通过例1,你能总结什么经验?
X 0 1
P 1-p p
归纳总结
求随机变量X的期望关键是写出分布列,一般分为四步:
(1)定值:确定随机变量X的所有可能取值;
(2)求概率:求出每种取值相应的概率;
(3)写分布列:写出随机变量X的分布列并检验;
(4)求期望:利用公式计算E ( X ).
典例剖析
例2 抛掷一枚质地均匀的骰子,设出现的点数为X,求X的均值.
新知探究
观察 掷一枚质地均匀的骰子,掷出的点数X的均值为3.5. 随机模拟这个试验,重复60次和重复300次各做6次,观测出现的点数并计算平均数. 根据观测值的平均数(样本均值)绘制统计图,分别如图 (1)和(2)所示. 观察图形,在两组试验中,随机变量的均值与样本均值有何联系与区别
探究:1、样本平均值和随机变量均值的区别与联系
新知探究
①区别: 随机变量的均值是一个常数,它不依赖于样本的抽取,而样本的平均值是一个随机变量,它随样本的不同而变化;
②联系: 对于简单随机样本,随着样本容量的增加样本的平均值越来越接近于总体的均值.因此我们常用样本的平均值估计总体的均值.
探究:1、样本平均值和随机变量均值的区别与联系
新知探究
探究 设Y=aX+b,其中a,b为常数,则Y也是随机变量.
(1) Y的分布列是什么? (2) E(Y)=?
探究:2、随机变量均值的性质
X X1 X2 ... Xi ... Xn
Y
P
新知生成
离散型随机变量均值的运算性质:
(1) E (X+b)=E (X )+b,
(2) E (aX )=aE (X ),
(3) E (aX+b )=aE (X )+b.
小试牛刀
m
典例剖析
例3 猜歌名游戏是根据歌曲的主旋律制成的铃声来猜歌名.某嘉宾参加猜歌名节目,猜对每首歌曲的歌名相互独立,猜对三首歌曲A,B,C歌名的概率及猜对时获得相应的公益基金如表所示.
歌曲 A B C
猜对的概率 0.8 0.6 0.4
获得的公益基金额/元 1000 2000 3000
规则如下:按照A,B,C的顺序猜,只有猜对当前歌曲的歌名才有资格猜下一首.求嘉宾获得的公益基金总额X的分布列及均值.
典例剖析
典例剖析
思考1: 如果改变猜歌的顺序,获得公益基金的均值是否相同?如果按ACB的顺序来猜歌,获得的公益基金的均值是多少?
典例剖析
思考2: 你认为哪个顺序获得的公益基金均值最大?
按由易到难的顺序来猜歌,获得的公益基金的均值最大;对于例3,决策的原则是选择期望值大的猜歌顺序,这称为期望值原则.
典例剖析
例4 根据气象预报,某地区近期有小洪水的概率为0.25,有大洪水的概率为0.01,该地区某工地上有一台大型设备,遇到大洪水时要损失60000元,遇到小洪水时要损失10000元.为保护设备,有以下3种方案:
方案1:运走设备,搬运费为3800元;
方案2:建保护围墙,建设费为2000元,但围墙只能防小洪水;
方案3:不采取措施.
工地的领导该如何决策呢?
典例剖析
典例剖析
巩固练习
1. 甲乙两台机床生产同一种零件,他们生产的产量相同,在1h内生产出的次品数分别为X1,X2,其分布列分别为
哪台机床更好?请解释你所得结论的实际意义.
巩固练习
2.盒子中装有编号为1,2,3,4,5,6的六个球.
(1)从中任意取出两个球,求这两个球的编号之和为偶数的概率;
(2)从中任意取出三个球,记X为编号为偶数的球的个数,求X的分布列和数学期望.
课堂小结
谢谢您的收看
第七章 随机变量及其分布
7.3.1 离散型随机变量的均值
复习旧知
1、离散型随机变量的分布列
一般地,设离散型随机变量X的可能取值为x1,x2,…,xn,我们称X取每一个值xi的概率P(X=xi)=pi,i=1,2,…,n为X的概率分布列,简称分布列.
2、两点分布列
X 0 1
P 1-p p
复习旧知
3、数据的均值和方差
已知一组样本数据:x1,x2,…,xn
样本均值:
样本方差:
学习目标
1. 理解离散型随机变量均值的概念和含义,会根据离散型随机变量的分布列求出均值;
2. 掌握离散型随机变量的均值的性质和两点分布的均值;
3. 会利用离散型随机变量的均值反映离散型随机变量的取值水平,解决一些相关的实际问题.
4. 核心素养: 数据分析、逻辑推理、数学运算。
情境导学
情境一:某人射击10次,所得环数分别是:1,1,1,1,2,2,2,3,3,4;则所得的平均环数是多少?
权数
情境导学
情境二:甲、乙两名射箭运动员射中目标箭靶的环数的分布列如下表所示:
环数X 7 8 9 10
甲射中的概率 0.1 0.2 0.3 0.4
乙射中的概率 0.15 0.25 0.4 0.2
如何比较他们射箭水平的高低呢
情境导学
假设甲射箭n次,射中7环、8环、9环和10环的频率分别为
甲n次射箭射中的平均环数为
当n足够大时,频率稳定于概率,所以 稳定于
即甲射中平均环数的稳定值为9,该值可以反映甲运动员的射箭水平.
所以,从平均值的角度比较,甲运动员的射箭水平比乙运动员高.
同理得乙射中环数的平均值:70.15+80.25+90.4+100.2=8.65.
情境导学
情境三:某商场要将单价分别为18元/kg,24元/kg,36元/kg的3种糖果按3:2:1的比例混合销售,如何对混合糖果定价才合理?
如果用X表示一颗糖果对应的单价,请写出随机变量X的分布列.
新知生成
一般地,若离散型随机变量X的分布列为:
离散型随机变量的均值(数学期望):
X x1 x2 ... xn
P p1 p2 ... pn
则称
1+2+...+
为随机变量X的均值或数学期望,简称期望. 它反映了离散型随机变量取值的平均水平.
典例剖析
例1 在篮球比赛中,罚球命中1次得1分,不中得0分. 如果某运动员罚球命中的概率为0.8,那么他罚球1次的得分X的均值是多少
解: 因为P(X=1)=0.8 , P(X=0)=0.2 ,
所以E(X)=0 × 0.2 + 1 × 0.8=0.8 .
即该运动员罚球1次的得分X的均值是0.8 .
思考:通过例1,你能总结什么经验?
X 0 1
P 1-p p
归纳总结
求随机变量X的期望关键是写出分布列,一般分为四步:
(1)定值:确定随机变量X的所有可能取值;
(2)求概率:求出每种取值相应的概率;
(3)写分布列:写出随机变量X的分布列并检验;
(4)求期望:利用公式计算E ( X ).
典例剖析
例2 抛掷一枚质地均匀的骰子,设出现的点数为X,求X的均值.
新知探究
观察 掷一枚质地均匀的骰子,掷出的点数X的均值为3.5. 随机模拟这个试验,重复60次和重复300次各做6次,观测出现的点数并计算平均数. 根据观测值的平均数(样本均值)绘制统计图,分别如图 (1)和(2)所示. 观察图形,在两组试验中,随机变量的均值与样本均值有何联系与区别
探究:1、样本平均值和随机变量均值的区别与联系
新知探究
①区别: 随机变量的均值是一个常数,它不依赖于样本的抽取,而样本的平均值是一个随机变量,它随样本的不同而变化;
②联系: 对于简单随机样本,随着样本容量的增加样本的平均值越来越接近于总体的均值.因此我们常用样本的平均值估计总体的均值.
探究:1、样本平均值和随机变量均值的区别与联系
新知探究
探究 设Y=aX+b,其中a,b为常数,则Y也是随机变量.
(1) Y的分布列是什么? (2) E(Y)=?
探究:2、随机变量均值的性质
X X1 X2 ... Xi ... Xn
Y
P
新知生成
离散型随机变量均值的运算性质:
(1) E (X+b)=E (X )+b,
(2) E (aX )=aE (X ),
(3) E (aX+b )=aE (X )+b.
小试牛刀
m
典例剖析
例3 猜歌名游戏是根据歌曲的主旋律制成的铃声来猜歌名.某嘉宾参加猜歌名节目,猜对每首歌曲的歌名相互独立,猜对三首歌曲A,B,C歌名的概率及猜对时获得相应的公益基金如表所示.
歌曲 A B C
猜对的概率 0.8 0.6 0.4
获得的公益基金额/元 1000 2000 3000
规则如下:按照A,B,C的顺序猜,只有猜对当前歌曲的歌名才有资格猜下一首.求嘉宾获得的公益基金总额X的分布列及均值.
典例剖析
典例剖析
思考1: 如果改变猜歌的顺序,获得公益基金的均值是否相同?如果按ACB的顺序来猜歌,获得的公益基金的均值是多少?
典例剖析
思考2: 你认为哪个顺序获得的公益基金均值最大?
按由易到难的顺序来猜歌,获得的公益基金的均值最大;对于例3,决策的原则是选择期望值大的猜歌顺序,这称为期望值原则.
典例剖析
例4 根据气象预报,某地区近期有小洪水的概率为0.25,有大洪水的概率为0.01,该地区某工地上有一台大型设备,遇到大洪水时要损失60000元,遇到小洪水时要损失10000元.为保护设备,有以下3种方案:
方案1:运走设备,搬运费为3800元;
方案2:建保护围墙,建设费为2000元,但围墙只能防小洪水;
方案3:不采取措施.
工地的领导该如何决策呢?
典例剖析
典例剖析
巩固练习
1. 甲乙两台机床生产同一种零件,他们生产的产量相同,在1h内生产出的次品数分别为X1,X2,其分布列分别为
哪台机床更好?请解释你所得结论的实际意义.
巩固练习
2.盒子中装有编号为1,2,3,4,5,6的六个球.
(1)从中任意取出两个球,求这两个球的编号之和为偶数的概率;
(2)从中任意取出三个球,记X为编号为偶数的球的个数,求X的分布列和数学期望.
课堂小结
谢谢您的收看
