1.6利用三角函数测高同步练习(无答案)2023—2024学年北师大版数学九年级下册
文档属性
| 名称 | 1.6利用三角函数测高同步练习(无答案)2023—2024学年北师大版数学九年级下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 177.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-23 11:57:37 | ||
图片预览


文档简介
1.6利用三角函数测高同步练习2023—2024学年北师大版数学九年级下册
一、单选题
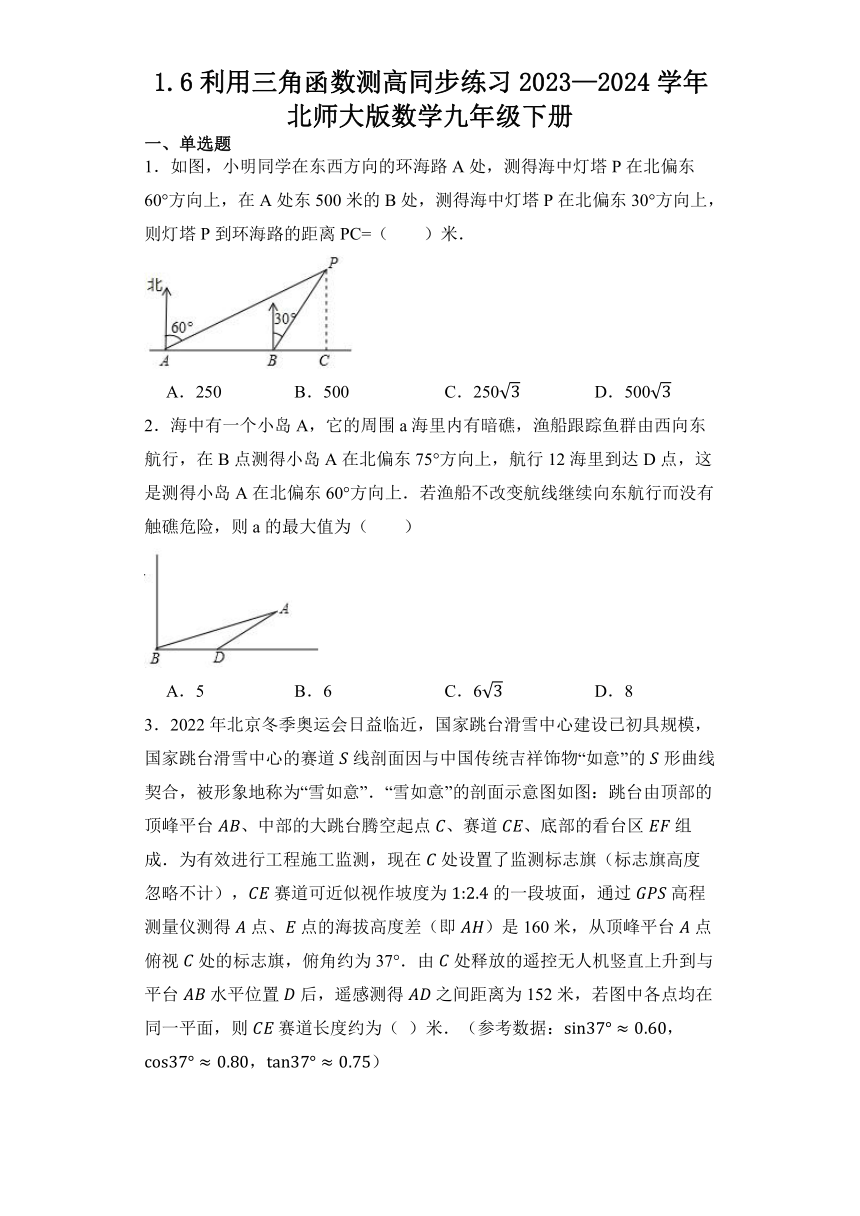
1.如图,小明同学在东西方向的环海路A处,测得海中灯塔P在北偏东60°方向上,在A处东500米的B处,测得海中灯塔P在北偏东30°方向上,则灯塔P到环海路的距离PC=( )米.
A.250 B.500 C.250 D.500
2.海中有一个小岛A,它的周围a海里内有暗礁,渔船跟踪鱼群由西向东航行,在B点测得小岛A在北偏东75°方向上,航行12海里到达D点,这是测得小岛A在北偏东60°方向上.若渔船不改变航线继续向东航行而没有触礁危险,则a的最大值为( )
A.5 B.6 C.6 D.8
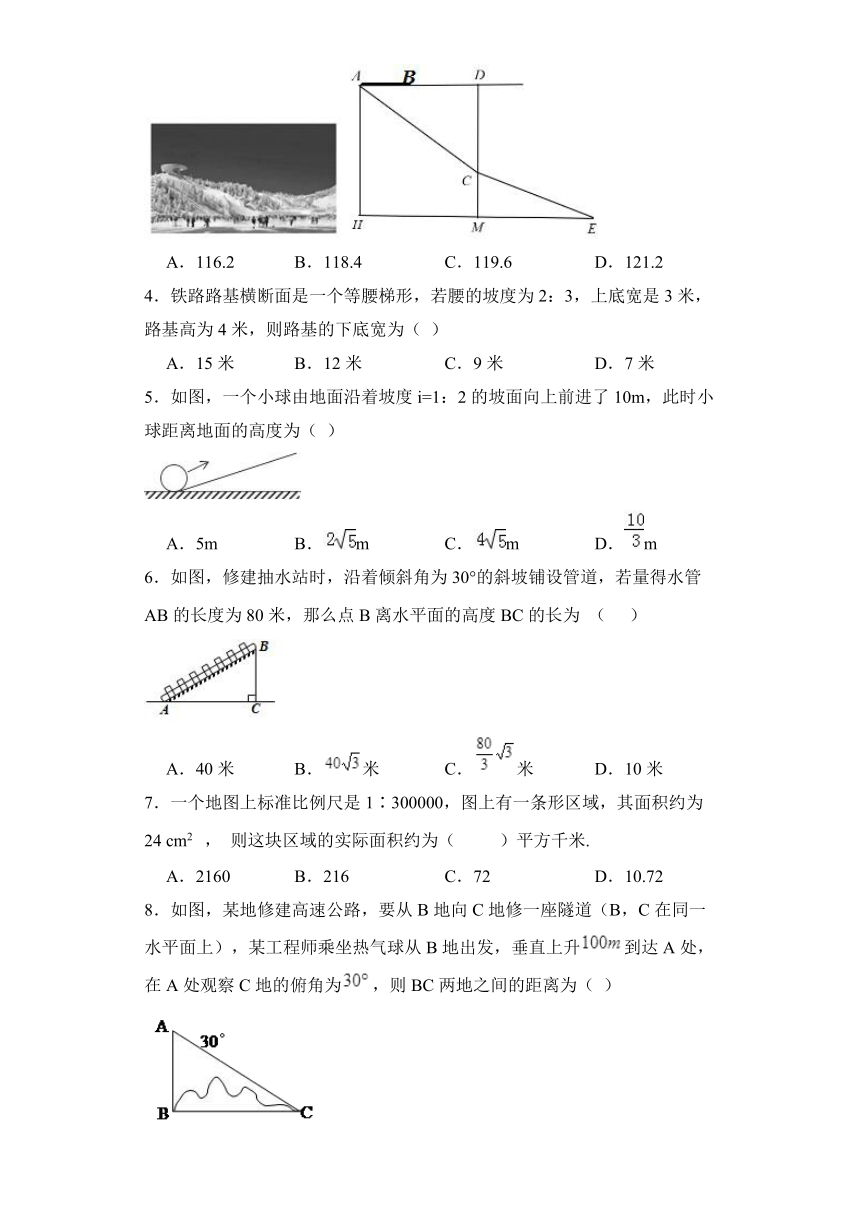
3.2022年北京冬季奥运会日益临近,国家跳台滑雪中心建设已初具规模,国家跳台滑雪中心的赛道线剖面因与中国传统吉祥饰物“如意”的形曲线契合,被形象地称为“雪如意”.“雪如意”的剖面示意图如图:跳台由顶部的顶峰平台、中部的大跳台腾空起点、赛道、底部的看台区组成.为有效进行工程施工监测,现在处设置了监测标志旗(标志旗高度忽略不计),赛道可近似视作坡度为的一段坡面,通过高程测量仪测得点、点的海拔高度差(即)是160米,从顶峰平台点俯视处的标志旗,俯角约为37°.由处释放的遥控无人机竖直上升到与平台水平位置后,遥感测得之间距离为152米,若图中各点均在同一平面,则赛道长度约为( )米.(参考数据:,,)
A.116.2 B.118.4 C.119.6 D.121.2
4.铁路路基横断面是一个等腰梯形,若腰的坡度为2:3,上底宽是3米,路基高为4米,则路基的下底宽为( )
A.15米 B.12米 C.9米 D.7米
5.如图,一个小球由地面沿着坡度i=1:2的坡面向上前进了10m,此时小球距离地面的高度为( )
A.5m B.m C.m D.m
6.如图,修建抽水站时,沿着倾斜角为30°的斜坡铺设管道,若量得水管AB的长度为80米,那么点B离水平面的高度BC的长为 ( )
A.40米 B.米 C.米 D.10米
7.一个地图上标准比例尺是1∶300000,图上有一条形区域,其面积约为24 cm2 , 则这块区域的实际面积约为( )平方千米.
A.2160 B.216 C.72 D.10.72
8.如图,某地修建高速公路,要从B地向C地修一座隧道(B,C在同一水平面上),某工程师乘坐热气球从B地出发,垂直上升到达A处,在A处观察C地的俯角为,则BC两地之间的距离为( )
A. B. C. D.
9.如图,某高楼顶部有一信号发射塔,在矩形建筑物ABCD的A,C两点测得该塔顶端F的仰角分别为45°和60°,矩形建筑物宽度AD=20 m,高度DC=30 m,则信号发射塔顶端到地面的高度(即FG的长)为( )
A.(35+55)m B.(25+45)m C.(25+75)m D.(50+20)m
10.某人沿着有一定坡度的坡面前进了10米,此时他与水平地面的垂直距离为2米,则这个坡面的坡度为( )
A.1:2 B.1:3 C.1: D.:1
二、填空题
11.一个斜坡的坡度是5:12,高度是4m,则他从坡底到坡顶部所走的路程大约是 m(精确到0.1m).
12.如图,某同学用一个有角的直角三角板估测学校旗杆AB的高度.他将与角相邻的直角边水平放在1.5m高的支架CD上,三角板的斜边与旗杆的顶点在同一直线上,他又量得DB的距离为5m,则旗杆AB的高度约为 m.(结果精确到lm,取1.73)
13.如图DABC 中, AB = 2 , BC = 4 , CD ^ AB 于 D , AE ^ BC 于 E , 则AE : CD = .
14.如图,河对岸有古塔AB,小敏在C处测得塔顶A的仰角为α,向塔走s米到达D,在D处测得塔顶A的仰角为β,则塔高是 米.
15.如右图所示,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为D、E,已知AB=6,AD=5,BC=4,则CE=
三、解答题
16.如图,热气球的探测器显示,从热气球看一栋高楼的顶部B的仰角为45°,看这栋高楼底的俯角为60°,热气球与高楼的水平距离AD 为20m,求这栋楼的高度.(结果保留根号)
17.如图所示,某数学活动小组要测量山坡上的电线杆PQ的高度.他们采取的方法是:先在地面上的点A处测得杆顶端点P的仰角是45°,再向前走到B点,测得杆顶端点P和杆底端点Q的仰角分别是60°和30°,这时只需要测出AB的长度就能通过计算求出电线杆PQ的高度.你同意他们的测量方案吗?若同意,画出计算时的图形,简要写出计算的思路,不用求出具体值;若不同意,提出你的测量方案,并简要写出计算思路.
18.北京的6月绿树成荫花成海,周末小明约了几个同到户外活动.当他们来到一座小亭子时,一位同学提议测量一下小亭子的高度,大家很高兴.于是设计出了这样一个测量方案:小明在小亭子和一棵小树的正中间点A的位置,观测小亭子顶端B的仰角∠BAC=60°,观测小树尖D的仰角∠DAE=45°.已知小树高DE=2米.请你也参与到这个活动中来,帮他们求出小亭子高BC的长.(结果精确到0.1.,)
19.安阳红旗渠机场于2023年11月29日正式通航,很多市民共同见证了这一历史时刻.如图,市民甲在处看见飞机A的仰角为45°,同时另一市民乙在斜坡上的处看见飞机A的仰角为30°,若斜坡的坡比,铅垂高度米(点、、、在同一水平线上).求飞机距离地面的高度.(结果保留根号)
20.如图,在热气球上A处测得塔顶B的仰角为52°,测得塔底C的俯角为45°,已知A处距地面98米,求塔高BC.(结果精确到0.1米)
【参考数据:sin52°=0.79,cos52°=0.62,tan52°=1.28】
21.如图,甲乙两建筑物之间的距离为24m,从甲的顶部C测得建筑物乙底部B的俯角为30°,从甲的顶部测得乙的顶部D的仰角为45°,求两建筑物的高.
一、单选题
1.如图,小明同学在东西方向的环海路A处,测得海中灯塔P在北偏东60°方向上,在A处东500米的B处,测得海中灯塔P在北偏东30°方向上,则灯塔P到环海路的距离PC=( )米.
A.250 B.500 C.250 D.500
2.海中有一个小岛A,它的周围a海里内有暗礁,渔船跟踪鱼群由西向东航行,在B点测得小岛A在北偏东75°方向上,航行12海里到达D点,这是测得小岛A在北偏东60°方向上.若渔船不改变航线继续向东航行而没有触礁危险,则a的最大值为( )
A.5 B.6 C.6 D.8
3.2022年北京冬季奥运会日益临近,国家跳台滑雪中心建设已初具规模,国家跳台滑雪中心的赛道线剖面因与中国传统吉祥饰物“如意”的形曲线契合,被形象地称为“雪如意”.“雪如意”的剖面示意图如图:跳台由顶部的顶峰平台、中部的大跳台腾空起点、赛道、底部的看台区组成.为有效进行工程施工监测,现在处设置了监测标志旗(标志旗高度忽略不计),赛道可近似视作坡度为的一段坡面,通过高程测量仪测得点、点的海拔高度差(即)是160米,从顶峰平台点俯视处的标志旗,俯角约为37°.由处释放的遥控无人机竖直上升到与平台水平位置后,遥感测得之间距离为152米,若图中各点均在同一平面,则赛道长度约为( )米.(参考数据:,,)
A.116.2 B.118.4 C.119.6 D.121.2
4.铁路路基横断面是一个等腰梯形,若腰的坡度为2:3,上底宽是3米,路基高为4米,则路基的下底宽为( )
A.15米 B.12米 C.9米 D.7米
5.如图,一个小球由地面沿着坡度i=1:2的坡面向上前进了10m,此时小球距离地面的高度为( )
A.5m B.m C.m D.m
6.如图,修建抽水站时,沿着倾斜角为30°的斜坡铺设管道,若量得水管AB的长度为80米,那么点B离水平面的高度BC的长为 ( )
A.40米 B.米 C.米 D.10米
7.一个地图上标准比例尺是1∶300000,图上有一条形区域,其面积约为24 cm2 , 则这块区域的实际面积约为( )平方千米.
A.2160 B.216 C.72 D.10.72
8.如图,某地修建高速公路,要从B地向C地修一座隧道(B,C在同一水平面上),某工程师乘坐热气球从B地出发,垂直上升到达A处,在A处观察C地的俯角为,则BC两地之间的距离为( )
A. B. C. D.
9.如图,某高楼顶部有一信号发射塔,在矩形建筑物ABCD的A,C两点测得该塔顶端F的仰角分别为45°和60°,矩形建筑物宽度AD=20 m,高度DC=30 m,则信号发射塔顶端到地面的高度(即FG的长)为( )
A.(35+55)m B.(25+45)m C.(25+75)m D.(50+20)m
10.某人沿着有一定坡度的坡面前进了10米,此时他与水平地面的垂直距离为2米,则这个坡面的坡度为( )
A.1:2 B.1:3 C.1: D.:1
二、填空题
11.一个斜坡的坡度是5:12,高度是4m,则他从坡底到坡顶部所走的路程大约是 m(精确到0.1m).
12.如图,某同学用一个有角的直角三角板估测学校旗杆AB的高度.他将与角相邻的直角边水平放在1.5m高的支架CD上,三角板的斜边与旗杆的顶点在同一直线上,他又量得DB的距离为5m,则旗杆AB的高度约为 m.(结果精确到lm,取1.73)
13.如图DABC 中, AB = 2 , BC = 4 , CD ^ AB 于 D , AE ^ BC 于 E , 则AE : CD = .
14.如图,河对岸有古塔AB,小敏在C处测得塔顶A的仰角为α,向塔走s米到达D,在D处测得塔顶A的仰角为β,则塔高是 米.
15.如右图所示,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为D、E,已知AB=6,AD=5,BC=4,则CE=
三、解答题
16.如图,热气球的探测器显示,从热气球看一栋高楼的顶部B的仰角为45°,看这栋高楼底的俯角为60°,热气球与高楼的水平距离AD 为20m,求这栋楼的高度.(结果保留根号)
17.如图所示,某数学活动小组要测量山坡上的电线杆PQ的高度.他们采取的方法是:先在地面上的点A处测得杆顶端点P的仰角是45°,再向前走到B点,测得杆顶端点P和杆底端点Q的仰角分别是60°和30°,这时只需要测出AB的长度就能通过计算求出电线杆PQ的高度.你同意他们的测量方案吗?若同意,画出计算时的图形,简要写出计算的思路,不用求出具体值;若不同意,提出你的测量方案,并简要写出计算思路.
18.北京的6月绿树成荫花成海,周末小明约了几个同到户外活动.当他们来到一座小亭子时,一位同学提议测量一下小亭子的高度,大家很高兴.于是设计出了这样一个测量方案:小明在小亭子和一棵小树的正中间点A的位置,观测小亭子顶端B的仰角∠BAC=60°,观测小树尖D的仰角∠DAE=45°.已知小树高DE=2米.请你也参与到这个活动中来,帮他们求出小亭子高BC的长.(结果精确到0.1.,)
19.安阳红旗渠机场于2023年11月29日正式通航,很多市民共同见证了这一历史时刻.如图,市民甲在处看见飞机A的仰角为45°,同时另一市民乙在斜坡上的处看见飞机A的仰角为30°,若斜坡的坡比,铅垂高度米(点、、、在同一水平线上).求飞机距离地面的高度.(结果保留根号)
20.如图,在热气球上A处测得塔顶B的仰角为52°,测得塔底C的俯角为45°,已知A处距地面98米,求塔高BC.(结果精确到0.1米)
【参考数据:sin52°=0.79,cos52°=0.62,tan52°=1.28】
21.如图,甲乙两建筑物之间的距离为24m,从甲的顶部C测得建筑物乙底部B的俯角为30°,从甲的顶部测得乙的顶部D的仰角为45°,求两建筑物的高.
