重点单元达标练习:运算律(拔高篇)数学四年级下册人教版(含答案)
文档属性
| 名称 | 重点单元达标练习:运算律(拔高篇)数学四年级下册人教版(含答案) | 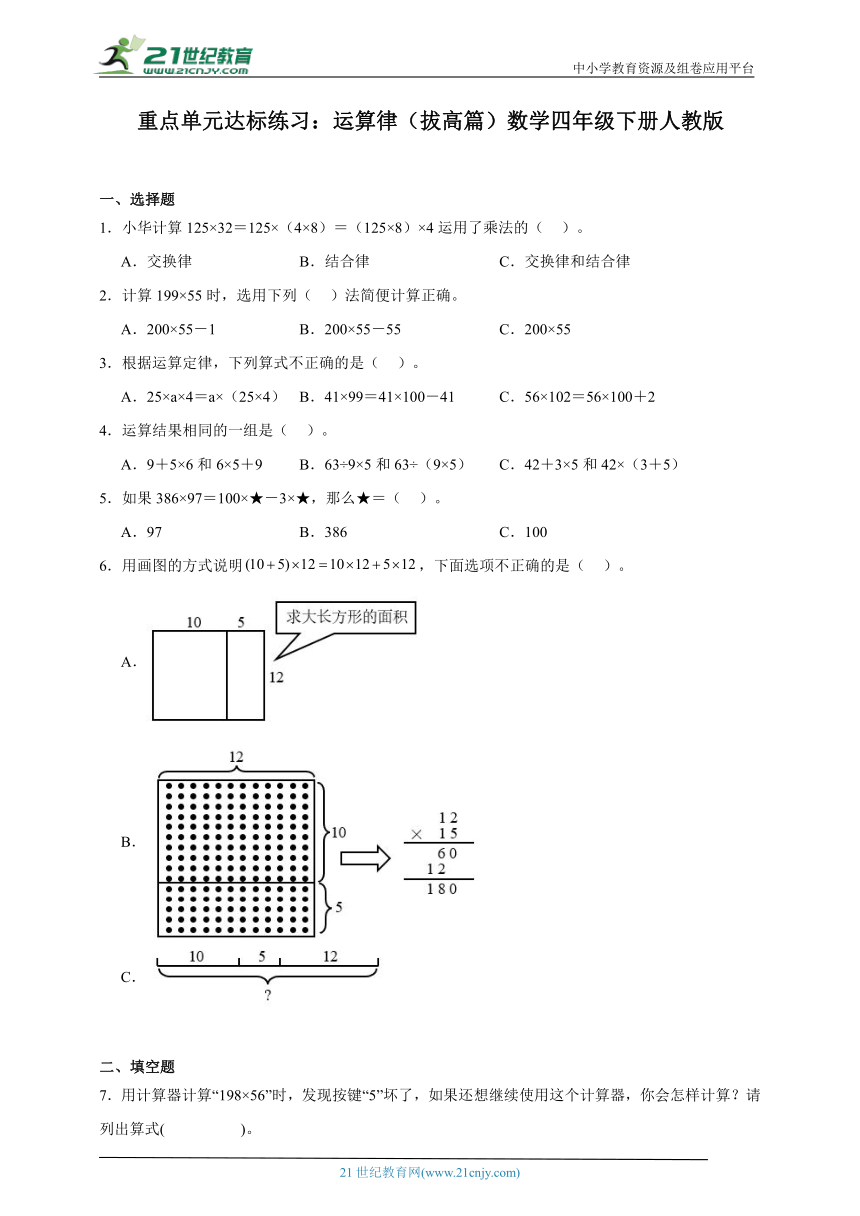 | |
| 格式 | docx | ||
| 文件大小 | 429.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-24 21:35:57 | ||
图片预览





文档简介
中小学教育资源及组卷应用平台
重点单元达标练习:运算律(拔高篇)数学四年级下册人教版
一、选择题
1.小华计算125×32=125×(4×8)=(125×8)×4运用了乘法的( )。
A.交换律 B.结合律 C.交换律和结合律
2.计算199×55时,选用下列( )法简便计算正确。
A.200×55-1 B.200×55-55 C.200×55
3.根据运算定律,下列算式不正确的是( )。
A.25×a×4=a×(25×4) B.41×99=41×100-41 C.56×102=56×100+2
4.运算结果相同的一组是( )。
A.9+5×6和6×5+9 B.63÷9×5和63÷(9×5) C.42+3×5和42×(3+5)
5.如果386×97=100×★-3×★,那么★=( )。
A.97 B.386 C.100
6.用画图的方式说明,下面选项不正确的是( )。
A.
B.
C.
二、填空题
7.用计算器计算“198×56”时,发现按键“5”坏了,如果还想继续使用这个计算器,你会怎样计算?请列出算式( )。
8.35×99+35=35×( ),运用了( )律。
9.在计算125×88时,聪聪是这样想的:125×88=125×(80+8)=125×80+125×8=10000+1000=11000,这是运用了( )律。
10.如果△+○=75,那么120-△-○=( )。
11.如果△+○=4,那么25×△+25×〇=( )。
12.根据运算定律或运算性质把算式补充完整。
48×19+57×48=_______〇(_______〇_______)
693÷21÷3=_______÷(_______〇_______)
三、判断题
13.131-64+36=131-(64+36)。( )
14.305×12=300×12+6。( )
15.◆+□+▲=◆+▲+□。( )
16.用竖式计算的过程中,运用了乘法结合律。( )
17.在计算时,一定要按四则混合运算的顺序,先算乘法,最后算加法。( )
四、计算题
18.直接写出结果。
0×27= 500×60= 240×3= 25×3×4=
608×92≈ 12×30= 125×8= 35×2×5=
19.下面各题,怎样简便就怎样算。
20.列式计算。
72与46的和,乘350减去143的差,积是多少?
五、解答题
21.少先队的主要教育方式是活动,在活动中将学生培养成为“四有”新人。希望小学少先队员共有25个中队,每个中队又分成4个小队。全校共有少先队员1200人,平均每个小队有多少人?
22.织布厂有16台织布机,平均每台织布机每小时织布8米,这些织布机125小时织布多少千米?
23.一张课桌158元,一把椅子42元,买30套课桌椅一共要付多少元?
24.学校买来10套办公桌椅(一张桌子配一把椅子),每张桌子205元,每把椅子95元。一共用了多少钱?
25.奶牛场有5个牛棚,每个牛棚里有4头奶牛,奶牛场一天共喂360kg饲料。平均每头奶牛一天喂多少千克饲料?(用两种方法解答)
26.甲乙两辆汽车同时从A地背向而行,甲车的速度是45千米/小时,乙车的速度是55千米/小时,3小时后,两车相距多少千米?
参考答案:
1.C
【分析】乘法结合律的特点是三个数相乘,先把前两个数相乘,或先把后两个数相乘,积不变。
乘法交换律的特点是两个数相乘,交换两个因数的位置,积不变;依此选择即可。
【详解】125×32=125×(4×8)=(125×8)×4,此算式先将32写成4×8,这是运用了乘法结合律,再交换8与4的位置,这是运用了乘法交换律,因此小华计算125×32=125×(4×8)=(125×8)×4运用了乘法的交换律和结合律。
故答案为:C
【点睛】熟练掌握乘法结合律和交换律的特点是解答此题的关键。
2.B
【分析】计算199×55时,可以把199改写成(200-1),然后运用乘法分配律进行简便运算。
【详解】199×55
=(200-1)×55
=200×55-1×55
=200×55-55
=11000-55
=10945
所以计算199×55时,选用上列200×55-55法简便计算正确。
故答案为:B
【点睛】本题考查了运用定律进行简便运算的能力,要灵活运用乘法分配律。
3.C
【分析】(1)乘法交换律:两个数相乘,交换因数的位置它们的积不变,用字母表示为:a×b=b×a。
(2)乘法结合律:三个数相乘,先把前两个数相乘,再乘第三个数;或者先把后两个数相乘,再和第一个数相乘,它们的积不变,用字母表示为:(a×b)×c=a×(b×c)。
(3)乘法分配律:两个数的和同一个数相乘,等于把两个加数分别同这个数相乘,再把两个积加起来,结果不变,用字母表示为:a×(b+c)=a×b+a×c。据此进行解答。
【详解】A.25×a×4
=a×25×4
=a×(25×4)
正确运用了乘法交换律和乘法结合律;
B.41×99
=41×(100-1)
=41×100-41×1
=41×100-41
=4100-41
=4059
先把99写成了(100-1),再根据乘法分配律计算的,所以原题计算正确;
C.56×102
=56×(100+2)
=56×100+56×2
=5600+112
=5712
先把102拆成(100+2),再根据乘法分配律计算,56×102=56×(100+2)=56×100+56×2,所以原题计算错误。
故答案为:C
【点睛】熟练掌握乘法的运算定律是解答本题的关键。
4.A
【分析】A.根据乘法交换律:两个数相乘,交换两个因数的位置,它们的积不变,用字母表示为a×b=b×a;进行判断;
B.63÷9×5先算除法,再算乘法,63÷(9×5)先算小括号里面的乘法,再算小括号外面的除法;
C.42+3×5先算乘法,再算加法,42×(3+5)先算小括号里面的加法,再算小括号外面的乘法。
【详解】A.9+5×6=6×5+9,交换两个因数的位置,它们的积不变,所以运算结果相同;
B.63÷9×5和63÷(9×5)运算顺序不相同,运算结果也不相同;
C.42+3×5和42×(3+5)运算顺序不相同,运算结果也不相同。
故答案为:A
【点睛】本题主要考查四则混合运算的顺序以及乘法交换律的灵活应用。
5.B
【分析】计算386×97时,可将97写成100-3,然后再根据乘法分配律的特点进行简算;
乘法分配律的其中一个特点是两个数的差与一个数相乘,可以先把它们与这个数分别相乘,再相减。
【详解】386×97=386×(100-3)=386×100-386×3,因此★=386。
故答案为:B
【点睛】熟练掌握乘法分配律的特点是解答此题的关键。
6.C
【分析】本题考查的知识点是乘法分配律,C选项表示的是10+5+12,与题目所给算式不符,据此解答。
【详解】A.表示;
B.表示;
C.表示。
故答案为:C
【点睛】熟练掌握整数乘法分配律并灵活运用是解答本题的关键。
7.198×7×8
【分析】56可写成7×8,则根据乘法结合律的特点可知:198×56=198×7×8,依此进行解答即可。
【详解】因此用计算器计算“198×56”时,发现按键“5”坏了,如果还想继续使用这个计算器,则可以这样计算:198×7×8。
【点睛】熟练掌握乘法结合律的特点是解答此题的关键。
8. 100/99+1 乘法分配/整数乘法分配
【分析】乘法分配律的特点是两个数的和与一个数相乘,可以先把它们与这个数分别相乘,再相加,依此进行填空即可。
【详解】35×99+35=35×(99+1)=35×100,运用了乘法分配律。
【点睛】熟练掌握乘法分配律的特点是解答此题的关键。
9.乘法分配
【分析】乘法分配律:a×(b+c)=a×b+a×c;据此即可解答。
【详解】在计算125×88时,聪聪是这样想的:125×88=125×(80+8)=125×80+125×8=10000+1000=11000,这是运用了乘法分配律。
【点睛】本题主要考查学生对乘法分配律的掌握和灵活运用。
10.45
【分析】减法的性质:一个数连续减去两个数,等于减去这两个数的和,用字母表示是:a-b-c=a-(b+c);120-△-○此算式可先根据减法的性质转化为120-(△+○),再根据如果△+○=75,代入数据计算即可得解。
【详解】如果△+○=75,那么
120-△-○
=120-(△+○)
=120-75
=45
如果△+○=75,那么120-△-○=45。
【点睛】本题考查了减法的性质,要熟练掌握,并灵活运用。
11.100
【分析】根据乘法分配律:ab+ac=a(b+c),解答即可。
【详解】
【点睛】本题考查了乘法分配律的灵活应用。
12.48;×;19;+;57
693;21;×;3
【分析】乘法分配律:a×(b+c)=a×b+a×c,除法的性质:a÷b÷c=a÷(b×c),据此即可解答。
【详解】48×19+57×48=48×(19+57)
693÷21÷3=693÷(21×3)
【点睛】本题主要考查学生对乘法分配律和除法的性质的掌握及灵活运用。
13.×
【分析】依据减法性质把等式右边的算式去掉括号,再与等式左边的算式比较解答。
【详解】依据减法性质可得等式的右边为:
131-(64+36)
=131-64-36
等式的左边=131-64+36
左边≠右边
故题干错误。
【点睛】此题主要考查学生对于减法性质的掌握,以及正确应用。
14.×
【分析】乘法分配律是指两个数的和同一个数相乘,等于把两个加数分别同这个数相乘,再把两个积加起来,结果不变;据此解答即可。
【详解】305×12
=(300+5)×12
=300×12+5×12
=300×12+60
故答案为:×。
【点睛】乘法分配律是乘法运算中非常重要的定律,需熟练掌握,达到能认会用的地步。
15.√
【分析】根据加法的交换律,交换任意两个加数的位置,结果保持不变。
【详解】◆+□+▲=◆+▲+□是利用加法交换律进行变形,原题干做说法正确。
故答案为:√
【点睛】本题考查的是加法交换律的应用,熟练掌握运算定律是关键。
16.×
【分析】根据乘法分配律是指两个数的和同一个数相乘,等于把两个加数分别同这个数相乘,再把两个积加起来,结果不变,本题是把28看成8+20,再根据乘法分配律进行计算。
【详解】45×28
=45×(8+20)
=45×8+45×20
=360+900
=1260
所以这个竖式在计算过程中运用了乘法分配律。
故答案为:×
【点睛】此题主要考查了学生对乘法分配律灵活掌握及运用。
17.×
【分析】在计算56×73+27×56时,也可以根据乘法分配律进行简算,也就是把56×73+27×56改写成56×(73+27),先计算小括号里面的加法,再算乘法,据此判断解答即可。
【详解】因为在四则混合运算中,先算乘除,再算加减,有括号的,应先算括号里面的,再算括号外面的;如能简算要简算。此说法不对。此算式可用乘法分配律进行简算:
56×73+27×56
=56×(73+27)
=56×100
=5600
故答案为:×
【点睛】本题考查了运算定律与简便运算,四则混合运算,注意运算顺序和运算法则,灵活运用所学的运算定律简便计算。
18.0;30000;720;300;
54000;360;1000;350;
【详解】略
19.1300;389;5500;
223;4900;352
【分析】(1)利用乘法结合律计算。三个数相乘,先把前两个数相乘,再和另外一个数相乘,或先把后两个数相乘,再和另外一个数相乘,积不变,叫做乘法结合律。
(2)利用加法结合律计算。三数相加,先把前面两个数相加,再和另一个数相加,或者先把后两个数相加,再加另一个数,和不变,这叫加法结合律。
(3)利用乘法分配律逆运算计算。在一个算式中,各项都含有共同的因数,那么可以把这个因数提到括号外面去,这便是提取公因数法。
(4)利用减法的性质计算,从一个数中连续减去两个数,就等于减去这两个数的和。
(5)利用乘法分配律逆运算计算。
(6)根据四则混合运算,先算除法,再算乘法,最后算减法。
【详解】4×13×25
=4×25×13
=100×13
=1300
267+89+33
=267+33+89
=300+89
=389
55×45+55×55
=55×(45+55)
=55×100
=5500
423-85-115
=423-(85+115)
=423-200
=223
49×101-49
=49×101-49×1
=49×(101-1)
=49×100
=4900
360-60÷15×2
=360-4×2
=360-8
=352
20.24426
【详解】(72+46)×(350-143)=24426
21.12人
【分析】少先队员的总人数÷中队的个数=平均每个中队的人数;平均每个中队的人数÷每个中队中小队的个数=平均每个小队的人数,依此列出综合算式并根据整数除法的性质进行简算。
【详解】1200÷25÷4
=1200÷(25×4)
=1200÷100
=12(人)
答:平均每个小队有12人。
【点睛】此题考查的是应用整数除法的性质解决实际问题,应熟练掌握。
22.16千米
【分析】织布机的台数×平均每台织布机每小时织布的长度×125=这些织布机125小时织布的长度,依此列式并根据乘法结合律的特点进行简算,最后根据1千米=1000米将单位化成千米即可。
【详解】16×8×125
=16×(8×125)
=16×1000
=16000(米)
16000米=16千米
答:这些织布机125小时织布16千米。
【点睛】此题考查的是工程问题的计算,以及千米和米之间的换算,应用乘法结合律的特点进行计算更加简便。
23.6000元
【分析】先算一套桌椅多少钱,再乘30即为所求。
【详解】(158+42)×30
=200×30
=6000(元)
答:买30套课桌椅一共要付6000元。
【点睛】本题考查了总价=单价×数量这一数量关系,还可以先用每张课桌的钱数乘30,求出课桌需要的总钱数,同理求出椅子需要的总钱数,再相加。
24.3000元
【分析】知道买来办公桌椅的数量,知道桌子、椅子的单价,可以用单价乘数量等于总价,分别算出桌子、椅子的总价,然后再算一共用了多少钱。也可以先算一套桌椅要多少钱,再乘数量,就得到10套桌椅要多少钱。
【详解】方法一:
205×10+95×10
=2050+950
=3000(元)
方法二:
(205+95)×10
=300×10
=3000(元)
答:一共用了3000元。
【点睛】本题考查学生对单价数量总价之间的关系掌握、以及运用乘法分配律解决问题。在购买多个物品时,如果数量一样,我们可以将多个物品的单价相加,求出单价之和,然后再乘数量,就能求出最后需要多少钱。
25.18千克
【分析】方法一:可先用饲料的总重量除以牛棚的个数计算出每个牛棚喂饲料的重量,然后用每个牛棚喂饲料的重量除以每个牛棚奶牛的头数即可,因此列式为:饲料的总重量÷牛棚的个数÷每个牛棚奶牛的头数=平均每头奶牛一天喂饲料的重量;
方法二:可先用牛棚的个数乘每个牛棚奶牛的头数计算出奶牛的总头数,然后用饲料的总重量除以奶牛的总头数即可,因此列式为:饲料的总重量÷(牛棚的个数×每个牛棚奶牛的头数)=平均每头奶牛一天喂饲料的重量。依此列式并计算。
【详解】方法一:
(千克)
方法二:
(千克)
答:平均每头奶牛一天喂18千克饲料。
【点睛】此题考查的是运用整数除法的性质解决实际问题,应熟练掌握。
26.300千米
【分析】首先用甲车的速度加上乙车的速度,求出两车的速度之和是多少,也就是两车1小时后相距多少千米;然后根据速度×时间=路程,用两车的速度之和乘时间,求出两车相距多少千米即可。
【详解】(45+55)×3
=100×3
=300(千米)
答:两车相距300千米。
【点睛】此题也可分别求出甲车3小时行的路程,乙车3小时行的路程,再相加,就是两车3小时后相距多少千米,可用乘法分配律进行简算:45×3+55×3=(45+55)×3。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
重点单元达标练习:运算律(拔高篇)数学四年级下册人教版
一、选择题
1.小华计算125×32=125×(4×8)=(125×8)×4运用了乘法的( )。
A.交换律 B.结合律 C.交换律和结合律
2.计算199×55时,选用下列( )法简便计算正确。
A.200×55-1 B.200×55-55 C.200×55
3.根据运算定律,下列算式不正确的是( )。
A.25×a×4=a×(25×4) B.41×99=41×100-41 C.56×102=56×100+2
4.运算结果相同的一组是( )。
A.9+5×6和6×5+9 B.63÷9×5和63÷(9×5) C.42+3×5和42×(3+5)
5.如果386×97=100×★-3×★,那么★=( )。
A.97 B.386 C.100
6.用画图的方式说明,下面选项不正确的是( )。
A.
B.
C.
二、填空题
7.用计算器计算“198×56”时,发现按键“5”坏了,如果还想继续使用这个计算器,你会怎样计算?请列出算式( )。
8.35×99+35=35×( ),运用了( )律。
9.在计算125×88时,聪聪是这样想的:125×88=125×(80+8)=125×80+125×8=10000+1000=11000,这是运用了( )律。
10.如果△+○=75,那么120-△-○=( )。
11.如果△+○=4,那么25×△+25×〇=( )。
12.根据运算定律或运算性质把算式补充完整。
48×19+57×48=_______〇(_______〇_______)
693÷21÷3=_______÷(_______〇_______)
三、判断题
13.131-64+36=131-(64+36)。( )
14.305×12=300×12+6。( )
15.◆+□+▲=◆+▲+□。( )
16.用竖式计算的过程中,运用了乘法结合律。( )
17.在计算时,一定要按四则混合运算的顺序,先算乘法,最后算加法。( )
四、计算题
18.直接写出结果。
0×27= 500×60= 240×3= 25×3×4=
608×92≈ 12×30= 125×8= 35×2×5=
19.下面各题,怎样简便就怎样算。
20.列式计算。
72与46的和,乘350减去143的差,积是多少?
五、解答题
21.少先队的主要教育方式是活动,在活动中将学生培养成为“四有”新人。希望小学少先队员共有25个中队,每个中队又分成4个小队。全校共有少先队员1200人,平均每个小队有多少人?
22.织布厂有16台织布机,平均每台织布机每小时织布8米,这些织布机125小时织布多少千米?
23.一张课桌158元,一把椅子42元,买30套课桌椅一共要付多少元?
24.学校买来10套办公桌椅(一张桌子配一把椅子),每张桌子205元,每把椅子95元。一共用了多少钱?
25.奶牛场有5个牛棚,每个牛棚里有4头奶牛,奶牛场一天共喂360kg饲料。平均每头奶牛一天喂多少千克饲料?(用两种方法解答)
26.甲乙两辆汽车同时从A地背向而行,甲车的速度是45千米/小时,乙车的速度是55千米/小时,3小时后,两车相距多少千米?
参考答案:
1.C
【分析】乘法结合律的特点是三个数相乘,先把前两个数相乘,或先把后两个数相乘,积不变。
乘法交换律的特点是两个数相乘,交换两个因数的位置,积不变;依此选择即可。
【详解】125×32=125×(4×8)=(125×8)×4,此算式先将32写成4×8,这是运用了乘法结合律,再交换8与4的位置,这是运用了乘法交换律,因此小华计算125×32=125×(4×8)=(125×8)×4运用了乘法的交换律和结合律。
故答案为:C
【点睛】熟练掌握乘法结合律和交换律的特点是解答此题的关键。
2.B
【分析】计算199×55时,可以把199改写成(200-1),然后运用乘法分配律进行简便运算。
【详解】199×55
=(200-1)×55
=200×55-1×55
=200×55-55
=11000-55
=10945
所以计算199×55时,选用上列200×55-55法简便计算正确。
故答案为:B
【点睛】本题考查了运用定律进行简便运算的能力,要灵活运用乘法分配律。
3.C
【分析】(1)乘法交换律:两个数相乘,交换因数的位置它们的积不变,用字母表示为:a×b=b×a。
(2)乘法结合律:三个数相乘,先把前两个数相乘,再乘第三个数;或者先把后两个数相乘,再和第一个数相乘,它们的积不变,用字母表示为:(a×b)×c=a×(b×c)。
(3)乘法分配律:两个数的和同一个数相乘,等于把两个加数分别同这个数相乘,再把两个积加起来,结果不变,用字母表示为:a×(b+c)=a×b+a×c。据此进行解答。
【详解】A.25×a×4
=a×25×4
=a×(25×4)
正确运用了乘法交换律和乘法结合律;
B.41×99
=41×(100-1)
=41×100-41×1
=41×100-41
=4100-41
=4059
先把99写成了(100-1),再根据乘法分配律计算的,所以原题计算正确;
C.56×102
=56×(100+2)
=56×100+56×2
=5600+112
=5712
先把102拆成(100+2),再根据乘法分配律计算,56×102=56×(100+2)=56×100+56×2,所以原题计算错误。
故答案为:C
【点睛】熟练掌握乘法的运算定律是解答本题的关键。
4.A
【分析】A.根据乘法交换律:两个数相乘,交换两个因数的位置,它们的积不变,用字母表示为a×b=b×a;进行判断;
B.63÷9×5先算除法,再算乘法,63÷(9×5)先算小括号里面的乘法,再算小括号外面的除法;
C.42+3×5先算乘法,再算加法,42×(3+5)先算小括号里面的加法,再算小括号外面的乘法。
【详解】A.9+5×6=6×5+9,交换两个因数的位置,它们的积不变,所以运算结果相同;
B.63÷9×5和63÷(9×5)运算顺序不相同,运算结果也不相同;
C.42+3×5和42×(3+5)运算顺序不相同,运算结果也不相同。
故答案为:A
【点睛】本题主要考查四则混合运算的顺序以及乘法交换律的灵活应用。
5.B
【分析】计算386×97时,可将97写成100-3,然后再根据乘法分配律的特点进行简算;
乘法分配律的其中一个特点是两个数的差与一个数相乘,可以先把它们与这个数分别相乘,再相减。
【详解】386×97=386×(100-3)=386×100-386×3,因此★=386。
故答案为:B
【点睛】熟练掌握乘法分配律的特点是解答此题的关键。
6.C
【分析】本题考查的知识点是乘法分配律,C选项表示的是10+5+12,与题目所给算式不符,据此解答。
【详解】A.表示;
B.表示;
C.表示。
故答案为:C
【点睛】熟练掌握整数乘法分配律并灵活运用是解答本题的关键。
7.198×7×8
【分析】56可写成7×8,则根据乘法结合律的特点可知:198×56=198×7×8,依此进行解答即可。
【详解】因此用计算器计算“198×56”时,发现按键“5”坏了,如果还想继续使用这个计算器,则可以这样计算:198×7×8。
【点睛】熟练掌握乘法结合律的特点是解答此题的关键。
8. 100/99+1 乘法分配/整数乘法分配
【分析】乘法分配律的特点是两个数的和与一个数相乘,可以先把它们与这个数分别相乘,再相加,依此进行填空即可。
【详解】35×99+35=35×(99+1)=35×100,运用了乘法分配律。
【点睛】熟练掌握乘法分配律的特点是解答此题的关键。
9.乘法分配
【分析】乘法分配律:a×(b+c)=a×b+a×c;据此即可解答。
【详解】在计算125×88时,聪聪是这样想的:125×88=125×(80+8)=125×80+125×8=10000+1000=11000,这是运用了乘法分配律。
【点睛】本题主要考查学生对乘法分配律的掌握和灵活运用。
10.45
【分析】减法的性质:一个数连续减去两个数,等于减去这两个数的和,用字母表示是:a-b-c=a-(b+c);120-△-○此算式可先根据减法的性质转化为120-(△+○),再根据如果△+○=75,代入数据计算即可得解。
【详解】如果△+○=75,那么
120-△-○
=120-(△+○)
=120-75
=45
如果△+○=75,那么120-△-○=45。
【点睛】本题考查了减法的性质,要熟练掌握,并灵活运用。
11.100
【分析】根据乘法分配律:ab+ac=a(b+c),解答即可。
【详解】
【点睛】本题考查了乘法分配律的灵活应用。
12.48;×;19;+;57
693;21;×;3
【分析】乘法分配律:a×(b+c)=a×b+a×c,除法的性质:a÷b÷c=a÷(b×c),据此即可解答。
【详解】48×19+57×48=48×(19+57)
693÷21÷3=693÷(21×3)
【点睛】本题主要考查学生对乘法分配律和除法的性质的掌握及灵活运用。
13.×
【分析】依据减法性质把等式右边的算式去掉括号,再与等式左边的算式比较解答。
【详解】依据减法性质可得等式的右边为:
131-(64+36)
=131-64-36
等式的左边=131-64+36
左边≠右边
故题干错误。
【点睛】此题主要考查学生对于减法性质的掌握,以及正确应用。
14.×
【分析】乘法分配律是指两个数的和同一个数相乘,等于把两个加数分别同这个数相乘,再把两个积加起来,结果不变;据此解答即可。
【详解】305×12
=(300+5)×12
=300×12+5×12
=300×12+60
故答案为:×。
【点睛】乘法分配律是乘法运算中非常重要的定律,需熟练掌握,达到能认会用的地步。
15.√
【分析】根据加法的交换律,交换任意两个加数的位置,结果保持不变。
【详解】◆+□+▲=◆+▲+□是利用加法交换律进行变形,原题干做说法正确。
故答案为:√
【点睛】本题考查的是加法交换律的应用,熟练掌握运算定律是关键。
16.×
【分析】根据乘法分配律是指两个数的和同一个数相乘,等于把两个加数分别同这个数相乘,再把两个积加起来,结果不变,本题是把28看成8+20,再根据乘法分配律进行计算。
【详解】45×28
=45×(8+20)
=45×8+45×20
=360+900
=1260
所以这个竖式在计算过程中运用了乘法分配律。
故答案为:×
【点睛】此题主要考查了学生对乘法分配律灵活掌握及运用。
17.×
【分析】在计算56×73+27×56时,也可以根据乘法分配律进行简算,也就是把56×73+27×56改写成56×(73+27),先计算小括号里面的加法,再算乘法,据此判断解答即可。
【详解】因为在四则混合运算中,先算乘除,再算加减,有括号的,应先算括号里面的,再算括号外面的;如能简算要简算。此说法不对。此算式可用乘法分配律进行简算:
56×73+27×56
=56×(73+27)
=56×100
=5600
故答案为:×
【点睛】本题考查了运算定律与简便运算,四则混合运算,注意运算顺序和运算法则,灵活运用所学的运算定律简便计算。
18.0;30000;720;300;
54000;360;1000;350;
【详解】略
19.1300;389;5500;
223;4900;352
【分析】(1)利用乘法结合律计算。三个数相乘,先把前两个数相乘,再和另外一个数相乘,或先把后两个数相乘,再和另外一个数相乘,积不变,叫做乘法结合律。
(2)利用加法结合律计算。三数相加,先把前面两个数相加,再和另一个数相加,或者先把后两个数相加,再加另一个数,和不变,这叫加法结合律。
(3)利用乘法分配律逆运算计算。在一个算式中,各项都含有共同的因数,那么可以把这个因数提到括号外面去,这便是提取公因数法。
(4)利用减法的性质计算,从一个数中连续减去两个数,就等于减去这两个数的和。
(5)利用乘法分配律逆运算计算。
(6)根据四则混合运算,先算除法,再算乘法,最后算减法。
【详解】4×13×25
=4×25×13
=100×13
=1300
267+89+33
=267+33+89
=300+89
=389
55×45+55×55
=55×(45+55)
=55×100
=5500
423-85-115
=423-(85+115)
=423-200
=223
49×101-49
=49×101-49×1
=49×(101-1)
=49×100
=4900
360-60÷15×2
=360-4×2
=360-8
=352
20.24426
【详解】(72+46)×(350-143)=24426
21.12人
【分析】少先队员的总人数÷中队的个数=平均每个中队的人数;平均每个中队的人数÷每个中队中小队的个数=平均每个小队的人数,依此列出综合算式并根据整数除法的性质进行简算。
【详解】1200÷25÷4
=1200÷(25×4)
=1200÷100
=12(人)
答:平均每个小队有12人。
【点睛】此题考查的是应用整数除法的性质解决实际问题,应熟练掌握。
22.16千米
【分析】织布机的台数×平均每台织布机每小时织布的长度×125=这些织布机125小时织布的长度,依此列式并根据乘法结合律的特点进行简算,最后根据1千米=1000米将单位化成千米即可。
【详解】16×8×125
=16×(8×125)
=16×1000
=16000(米)
16000米=16千米
答:这些织布机125小时织布16千米。
【点睛】此题考查的是工程问题的计算,以及千米和米之间的换算,应用乘法结合律的特点进行计算更加简便。
23.6000元
【分析】先算一套桌椅多少钱,再乘30即为所求。
【详解】(158+42)×30
=200×30
=6000(元)
答:买30套课桌椅一共要付6000元。
【点睛】本题考查了总价=单价×数量这一数量关系,还可以先用每张课桌的钱数乘30,求出课桌需要的总钱数,同理求出椅子需要的总钱数,再相加。
24.3000元
【分析】知道买来办公桌椅的数量,知道桌子、椅子的单价,可以用单价乘数量等于总价,分别算出桌子、椅子的总价,然后再算一共用了多少钱。也可以先算一套桌椅要多少钱,再乘数量,就得到10套桌椅要多少钱。
【详解】方法一:
205×10+95×10
=2050+950
=3000(元)
方法二:
(205+95)×10
=300×10
=3000(元)
答:一共用了3000元。
【点睛】本题考查学生对单价数量总价之间的关系掌握、以及运用乘法分配律解决问题。在购买多个物品时,如果数量一样,我们可以将多个物品的单价相加,求出单价之和,然后再乘数量,就能求出最后需要多少钱。
25.18千克
【分析】方法一:可先用饲料的总重量除以牛棚的个数计算出每个牛棚喂饲料的重量,然后用每个牛棚喂饲料的重量除以每个牛棚奶牛的头数即可,因此列式为:饲料的总重量÷牛棚的个数÷每个牛棚奶牛的头数=平均每头奶牛一天喂饲料的重量;
方法二:可先用牛棚的个数乘每个牛棚奶牛的头数计算出奶牛的总头数,然后用饲料的总重量除以奶牛的总头数即可,因此列式为:饲料的总重量÷(牛棚的个数×每个牛棚奶牛的头数)=平均每头奶牛一天喂饲料的重量。依此列式并计算。
【详解】方法一:
(千克)
方法二:
(千克)
答:平均每头奶牛一天喂18千克饲料。
【点睛】此题考查的是运用整数除法的性质解决实际问题,应熟练掌握。
26.300千米
【分析】首先用甲车的速度加上乙车的速度,求出两车的速度之和是多少,也就是两车1小时后相距多少千米;然后根据速度×时间=路程,用两车的速度之和乘时间,求出两车相距多少千米即可。
【详解】(45+55)×3
=100×3
=300(千米)
答:两车相距300千米。
【点睛】此题也可分别求出甲车3小时行的路程,乙车3小时行的路程,再相加,就是两车3小时后相距多少千米,可用乘法分配律进行简算:45×3+55×3=(45+55)×3。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
