安徽省2016年初中毕业学业考试模拟试题(含答案及评分标准)
文档属性
| 名称 | 安徽省2016年初中毕业学业考试模拟试题(含答案及评分标准) |

|
|
| 格式 | zip | ||
| 文件大小 | 262.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-09-21 00:00:00 | ||
图片预览

文档简介
安徽省2016年初中毕业学业考试模拟试卷
考生注意:本卷共八大题,计23小题,满分150分,考试时间120分钟.
一、选择题 (本题共10小题,每小题4分,满分40分).每一个小题都给出代号为A、B、C、D的四个结论,其中只有一个是正确的,把正确结论的代号写在题后的括号。每一小题:选对得 4分,不选、选错或选出的代号超过一个的(不论是否写在括号内)一律得0分。
1. 135. 下列运算结果是-2的是【 】
A.(-2)0 B.-|-2| C.2-1 D.-(-2)
2. 141. 据合肥市旅游局统计显示,2013年春节7天长假,合肥的景区、景点以及农家乐接待游客数量共达到265万人次,旅游总收入达到14.3亿元.其中14.3元亿用科学记数法表示是【 】
A.14.3×108元 B.1.43×108元 C.1.43×109元 D.14.3×109元
3. 147. 下列标志既是轴对称图形又是中心对称图形的是【 】
A. B. C. D.
4. 153. 下列调查适合普查的是【 】
A.调查2013年2月份合肥市场上某品牌饮料的质量
B.调查某月份长江安徽段水域的水质量情况
C.光明节能厂检测一批新型节能灯的使用寿命
D.了解某班50名学生的年龄情况
5. 159. 下列运算正确的是【 】
A.2a+3b=5ab B.2(a-b)=4a-b
C.(a+b)(a-b)=a2-b2 D.(a+b)2=a2+b2
6. 165. 为减轻用药负担,进一步改善群众的医疗条件,某品牌抗感染药氧氟沙星眼膏剂连续两次降价,由原来每支17.6元降至每支9.9元.若每次的降低率相同,则每次降低率为 【 】
A.15% B.20% C.25% D.30%
7. 171. 如图,AB是⊙O的直径,点C在⊙O上,若∠C=18°,
则∠BOC的度数是【 】
A.36° B.48° C.54° D.72°
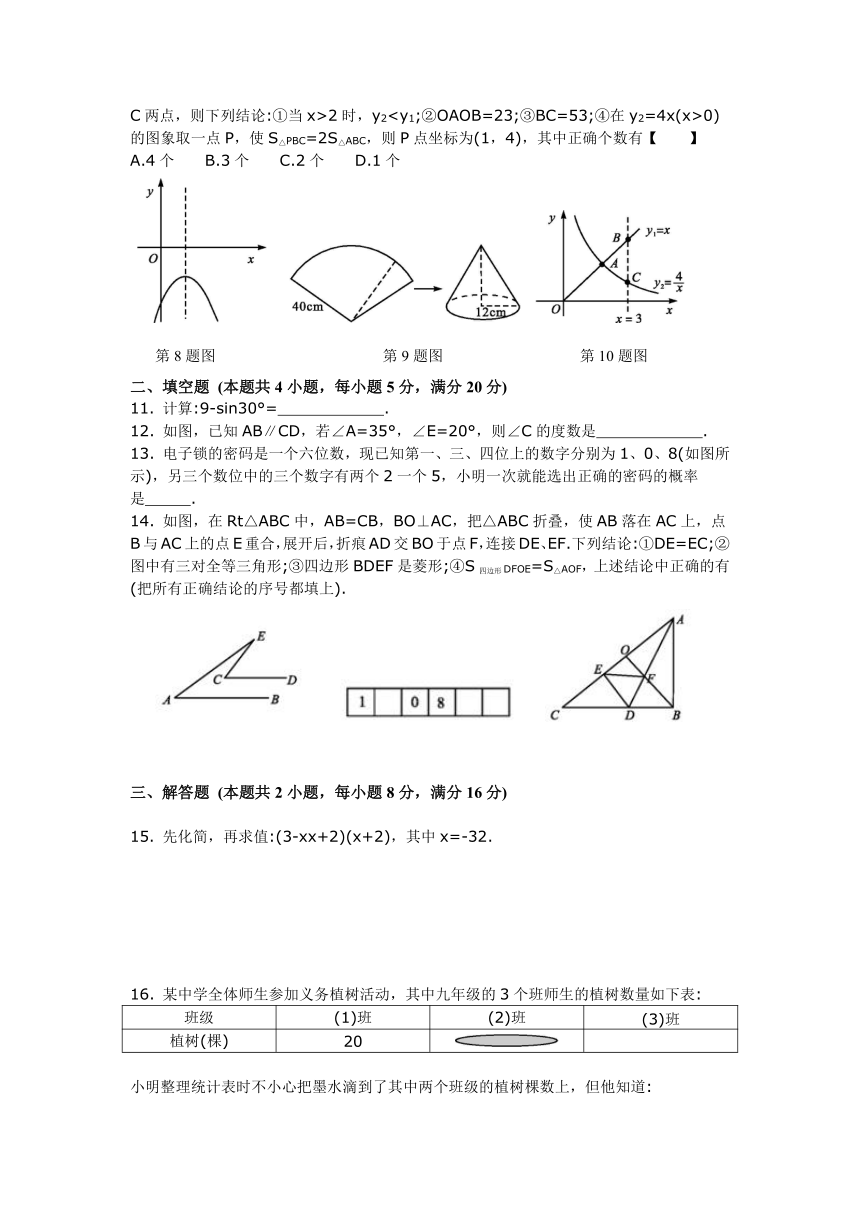
8. 177. 二次函数y=ax2+bx+c(a≠0)的图象如图,
下列判断错误的是【 】
A.a<0 B.b<0 C.c<0 D.b2-4ac<0
9. 183. 现有半径为40 cm,圆心角为120°的一个扇形彩铁皮,
工人师傅打算剪去一部分扇形后,利用剩下的扇形铁皮制作成一个底面半径为12 cm的圆锥形工具(接缝处不重叠),那么剪去的扇形的圆心角为【 】
A.12° B.15° C.25° D.30°
答案:A
解析:设剪去的扇形的圆心角为x,则由题意得,40(120-x)180 π=24π,解得x=12°.
C两点,则下列结论:①当x>2时,y20)的图象取一点P,使S△PBC=2S△ABC,则P点坐标为(1,4),其中正确个数有【 】
A.4个 B.3个 C.2个 D.1个
答案:A
解析:设P点坐标为(x,y),由y1=y2,即x=4x得x=2,x=-2(舍去),故A(2,2).由题意知,B(3,3),C(3,43),
所以BC=3-43=53,OA=22,OB=32,所以OAOB=23,S△ABC =12BC(3-2)=56,所以S△PBC=12BC(3-x)=2S△ABC
=53,即3-x=2,解得x=1,所以y=4,故P(1,4).又由图知,当x>2时,y2二、填空题 (本题共4小题,每小题5分,满分20分)
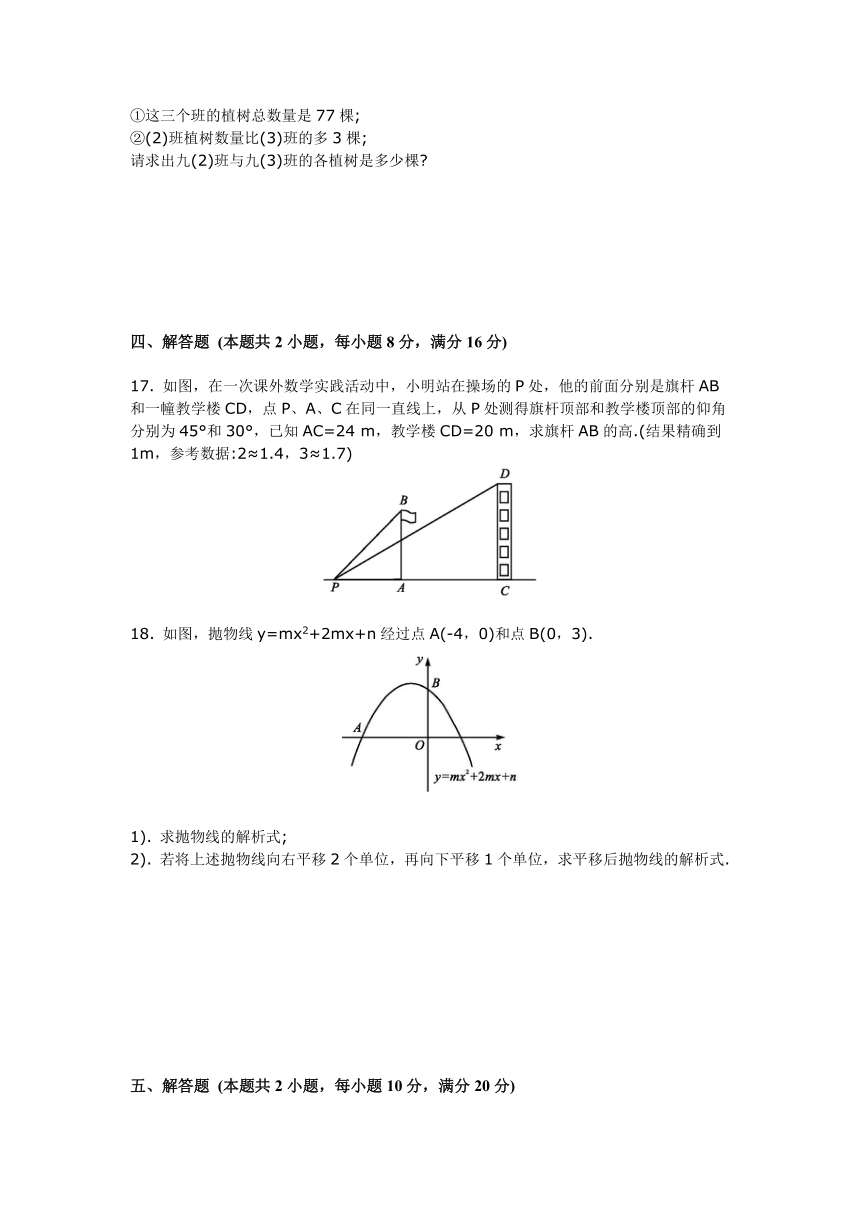
11. 196. 计算:9-sin30°= .
12. 198. 如图,已知AB∥CD,若∠A=35°,∠E=20°,则∠C的度数是 .
13. 200. 电子锁的密码是一个六位数,现已知第一、三、四位上的数字分别为1、0、8(如图所示),另三个数位中的三个数字有两个2一个5,小明一次就能选出正确的密码的概率是 .
14. 202. 如图,在Rt△ABC中,AB=CB,BO⊥AC,把△ABC折叠,使AB落在AC上,点B与AC上的点E重合,展开后,折痕AD交BO于点F,连接DE、EF.下列结论:①DE=EC;②图中有三对全等三角形;③四边形BDEF是菱形;④S四边形DFOE=S△AOF,上述结论中正确的有 (把所有正确结论的序号都填上).
三、解答题 (本题共2小题,每小题8分,满分16分)
15. 205. 先化简,再求值:(3-xx+2)(x+2),其中x=-32.
答案:解:原式=3x+6-xx+2·(x+2) 2分
=2(x+3)x+2·(x+2) 4分
=2x+6. 6分
当x=-32时,
原式=2×(-32)+6=3. 8分
16. 207. 某中学全体师生参加义务植树活动,其中九年级的3个班师生的植树数量如下表:
班级 (1)班 (2)班 (3)班
植树(棵) 20
小明整理统计表时不小心把墨水滴到了其中两个班级的植树棵数上,但他知道:
①这三个班的植树总数量是77棵;
②(2)班植树数量比(3)班的多3棵;
请求出九(2)班与九(3)班的各植树是多少棵
答案:解:设(2)班植树x棵,则20+x+(x-3)=77,3分
解得x=30,4分
30-3=27(棵).6分
答:九(2)班植树30棵,九(3)班植树27棵.8分
四、解答题 (本题共2小题,每小题8分,满分16分)
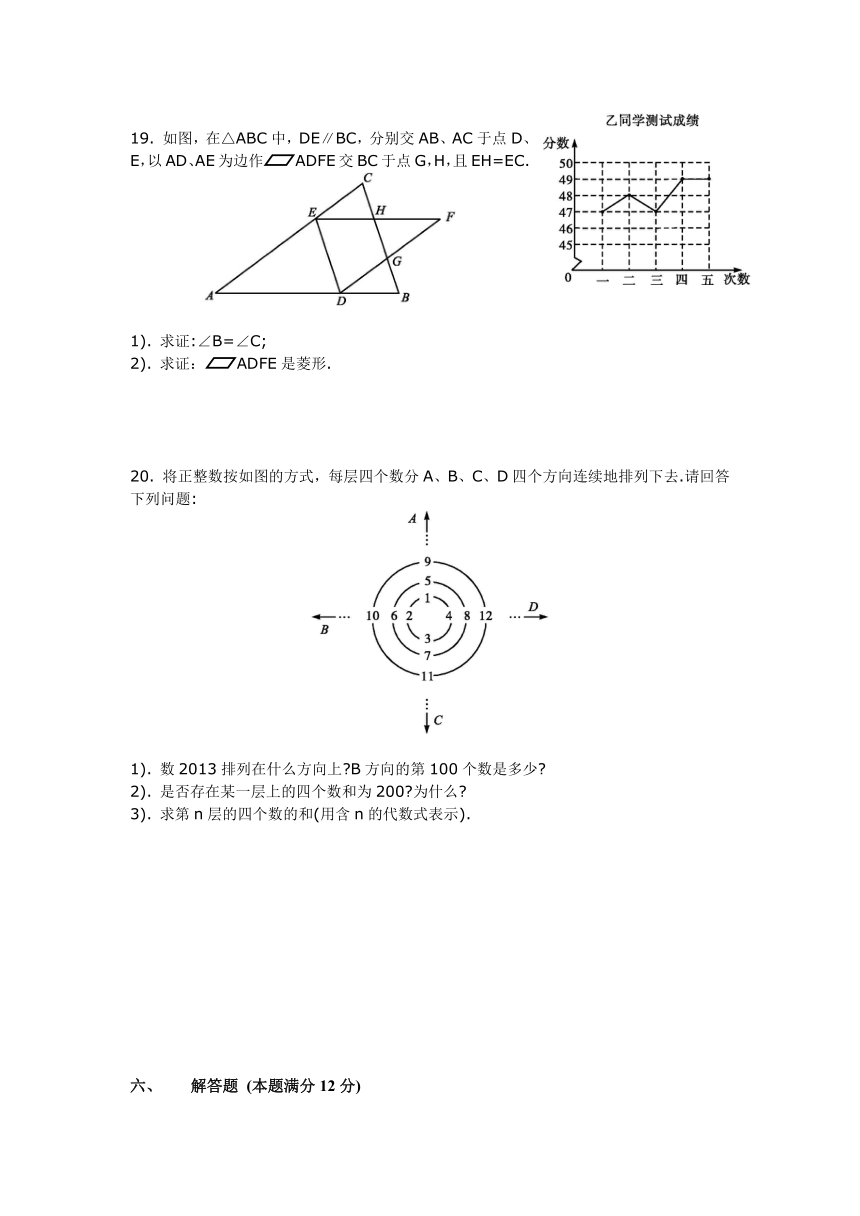
17. 211. 如图,在一次课外数学实践活动中,小明站在操场的P处,他的前面分别是旗杆AB和一幢教学楼CD,点P、A、C在同一直线上,从P处测得旗杆顶部和教学楼顶部的仰角分别为45°和30°,已知AC=24 m,教学楼CD=20 m,求旗杆AB的高.(结果精确到1m,参考数据:2≈1.4,3≈1.7)
答案:解:∵CD⊥PC,∠DPC=30°,
∴tan30°=CDPC.
即33=2024+PA,
∴PA=203-24≈10(m). 5分
∵AB⊥PA,∠APB=45°,
∴∠ABP=45°.
∴AB=PA=10(m).
答:旗杆CD高是10m. 8分
18. 213. 如图,抛物线y=mx2+2mx+n经过点A(-4,0)和点B(0,3).
1). 求抛物线的解析式;
答案:∵抛物线y=mx2+2mx+n经过点A(-4,0)和点B(0,3),
∴16m-8m+n=0,n=3. 2分
解得m=-38,n=3. 3分
∴抛物线的解析式为:y=-38x2-34x+3.4分
2). 若将上述抛物线向右平移2个单位,再向下平移1个单位,求平移后抛物线的解析式.
答案:∵y=-38x2-34x+3=-38(x+1)2+278.
∴将此抛物线向右平移2个单位,再向下平移1个单位的解析式为
y=-38(x+1-2)2+278-1
即y=-38(x-1)2+198. 8分
五、解答题 (本题共2小题,每小题10分,满分20分)
19. 219. 如图,在△ABC中,DE∥BC,分别交AB、AC于点D、E,以AD、AE为边作ADFE交BC于点G,H,且EH=EC.
1). 求证:∠B=∠C;
答案: ADFE中,AD∥EF,
∵∠EHC=∠B,又∵EH=EC,
∴∠EHC=∠C,3分
∴∠B=∠C.4分
2). 求证:ADFE是菱形.
答案:∵DE∥BC,
∴∠AED=∠C,∠ADE=∠B,6分
∵∠B=∠C,∴∠AED=∠ADE.8分
∴AD=AE,
∴ ADFE是菱形.10分
20. 224. 将正整数按如图的方式,每层四个数分A、B、C、D四个方向连续地排列下去.请回答下列问题:
1). 数2013排列在什么方向上 B方向的第100个数是多少
答案:数2013排列在A方向上;B方向的第100个数是398.3分
2). 是否存在某一层上的四个数和为200 为什么
答案:设某层上的四个数分别为x,x+1,x+2,x+3,
若x+(x+1)+(x+2)+(x+3)=200,5分
解得:x=972.
∵972不是正整数,
∴不存在某一层上的四个数和为200. 7分
3). 求第n层的四个数的和(用含n的代数式表示).
答案:第n层的四个数分别是4(n-1)+1,4(n-1)+2,4(n-1)+3,4n.8分
[4(n-1)+1]+[4(n-1)+2]+[4(n-1)+3]+4n
=16n-6.
即第n层的四个数的和是16n-6. 10分
六、 解答题 (本题满分12分)
21. 233. 九年级甲、乙两位学生积极进行体育训练,并在训练期间内先后进行了五次体育测试,甲同学的测试成绩如表,乙同学的测试成绩折线统计图如图所示:
甲同学测试成绩
次数 一 二 三 四 五
分数 46 47 48 49 50
1). 请根据甲、乙两同学五次体育测试的成绩填写下表:
中位数 平均数 方差
甲 48 2
乙 48
答案:甲:平均数48 乙:中位数48 方差0.8.3分
2). 甲、乙两同学这五次测试的成绩中,谁的变化相对平缓 为什么
答案:乙同学五次体育测试成绩较平缓.因为乙的五次测试成绩的方差和极差小于甲的方差和极差.6分
3). 在图中,画出甲的测试成绩的折线图,从甲、乙两同学这五次体育测试的成绩的折线图来看,甲、乙两位同学,谁的训练成效更为显著 请说明理由.
答案:图略,甲同学的训练成效更为显著.因为甲的五次测试成绩逐步上升,并由开始低于乙的成绩逐渐上升到高于乙的成绩.12分
七、 解答题 (本题满分12分)
22. 241. A、B两座城市之间有一条高速公路,甲、乙两辆汽车同时分别从这条路两端的入口处驶入,并始终在高速公路上正常行驶.甲车驶往B城,乙车驶往A城,甲车在行驶过程中速度始终不变.甲车距B城高速公路入口处的距离y(km)与行驶时间x(h)之间的关系如图所示.
1). 求y关于x的表达式;
答案:设y=kx+b,将(0,300),(2,120)代入得:
b=300,2k+b=120,解得k=-90,b=300.2分
所以y=-90x+300.3分
2). 在两车相遇前,乙车以60 km/h的速度匀速行驶;两车相遇后,乙车改变了行车速度并保持匀速行驶,结果共用了4 h到达A城.请求出两车相遇的时间,并在图中画出乙车离开B城高速公路入口处的距离y(km)与行驶时间x(h)之间的函数图象;
答案:由图象知:甲车的速度为90 km/h,4分
设两车出发后t时相遇,则90t+60t=300,5分
t=2.
即出发后2小时两车相遇.
乙车的图象略.8分
3). 在(2)的条件下,直接写出乙车变化后的速度,并求当甲车到达B城时两车相距多少千米
答案:乙车变化后的速度为90 km/h.9分
当y=0时,由0=-90x+300,得x=103.10分
此时,乙车距B城的距离是60×2+90×(103-2)=240 (km).12分
即当甲车到达B城时两车相距240 km.
八、 解答题 (本题满分14分)
23. 250. 阅读下面的材料:
如右图所示,P是等腰△ABC的底边BC上任一点,PE⊥AB于E,PF⊥AC于F,BH是腰AC上的高,求证:PE+PF=BH.
证明:连接AP,则有S△ABC=S△ABP+S△ACP,得
12AC×BH=12AC×PF+12AB×PE.
因为AB=AC,所以BH=PE+PH.
请你利用上面的结论或方法解答下列问题:
1). 如图①,P是边长为2的正方形ABCD边AD上任意一点,且PE⊥AC于E,PF⊥DB于F,求PE+PF的值;
答案:在等腰△OAD中,OA=OD.
∵PE⊥AC,PF⊥DB,腰OA上高为OD.由题结论可得PE+PF=OD.2分
又OD=12BD=2,∴PE+PF=2.4分
2). 如图②,P是等腰△ABC的底边BC的延长线上一点,PE⊥AB于E,PF⊥AC且交AC的延长线于F,BH是腰AC上的高,那么PE,PF与BH有何数量关系 并说明理由;
答案:关系是PE-PF=BH.5分
理由:连接AP,则有S△ABP-S△ACP=S△ABC,故
12AB·PE-12AC·PF=12AC·BH.8分
因为AB=AC,所以PE-PF=BH.9分
3). 如图③,在Rt△ABC中,∠A=90°,D是AB上一点,且BD=CD,过BC上任一点P作PE⊥DB于E,PF⊥DC于F,若tan∠B=12,BC=45,求PE+PF的值.
答案:在等腰△DBC中,DB=DC.11分
∵PE⊥DB,PF⊥DC,腰DB上高为AC.由此可得PE+PF=AC.
在Rt△ABC中,∠A=90°,∵tan B=ACAB=12,
设AC=x,则AB=2x.从而x2+(2x)2=(45)2,12分
解得x=4(负舍),∴PE+PF=AC=4.∴PE+PF=4. 14分
答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 B C A D C C A B A A
二、填空题
11. 52 12. 55° 13. 14. ① ③ ④
三、
15. 解:原式=3x+6-xx+2·(x+2) 2分
=2(x+3)x+2·(x+2) 4分
=2x+6. 6分
当x=-32时,
原式=2×(-32)+6=3. 8分
16. 解:设(2)班植树x棵,则20+x+(x-3)=77 3分
解得x=30 4分
30-3=27(棵) 6分
答:九(2)班植树30棵,九(3)班植树27棵 8分
四、
17. 解:∵CD⊥PC,∠DPC=30°,
∴tan30°=CDPC.
即33=2024+PA,
∴PA=203-24≈10(m) 5分
∵AB⊥PA,∠APB=45°,
∴∠ABP=45°.
∴AB=PA=10(m).
答:旗杆CD高是10m 8分
18. 1). 解:∵抛物线y=mx2+2mx+n经过点A(-4,0)和点B(0,3),
∴16m-8m+n=0,n=3 2分
解得m=-38,n=3 3分
∴抛物线的解析式为:y=-38x2-34x+3 4分
2).解:∵y=-38x2-34x+3=-38(x+1)2+278.
∴将此抛物线向右平移2个单位,再向下平移1个单位的解析式为
y=-38(x+1-2)2+278-1
即y=-38(x-1)2+198 8分
五、
19. 1). 证明: ADFE中,AD∥EF,
∴∠EHC=∠B,
又∵EH=EC,
∴∠EHC=∠C 3分
∴∠B=∠C 4分
2). 证明:∵DE∥BC,
∴∠AED=∠C,∠ADE=∠B 6分
∵∠B=∠C,
∴∠AED=∠ADE 8分
∴AD=AE,
∴ADFE是菱形 10分
20. 1). 答:数2013排列在A方向上;B方向的第100个数是398 3分
2). 解:设某层上的四个数分别为x,x+1,x+2,x+3,
若x+(x+1)+(x+2)+(x+3)=200 5分
解得:x=.
∵不是正整数,
∴不存在某一层上的四个数和为200 7分
3). 解:第n层的四个数分别是4(n-1)+1,4(n-1)+2,4(n-1)+3,4n 8分
[4(n-1)+1]+[4(n-1)+2]+[4(n-1)+3]+4n
=16n-6.
即第n层的四个数的和是16n-6 10分
六、
21. 1). 答:甲:平均数48 乙:中位数48 方差0.8 3分
2). 答:乙同学五次体育测试成绩较平缓.因为乙的五次测试成绩的
方差和极差小于甲的方差和极差 6分
3). 答:图略,甲同学的训练成效更为显著.因为甲的五次测试成绩逐步上升,
并由开始低于乙的成绩逐渐上升到高于乙的成绩 12分
七、
22. 1). 解:设y=kx+b,将(0,300),(2,120)代入得:
解得k=-90,b=300 2分
所以y=-90x+300 3分
2). 解:由图象知:甲车的速度为90 km/h 4分
设两车出发后t时相遇,则90t+60t=300 5分
t=2.
即出发后2小时两车相遇.
乙车的图象略 8分
3). 解:乙车变化后的速度为90 km/h 9分
当y=0时,由0=-90x+300,得x=103 10分
此时,乙车距B城的距离是60×2+90×(103-2)=240 (km) 12分
即当甲车到达B城时两车相距240 km.
八、
23. 1). 解:在等腰△OAD中,OA=OD.
∵PE⊥AC,PF⊥DB, 腰OA上高为OD.
由题结论可得PE+PF=OD 2分
又OD=BD=2,
∴PE+PF=2 4分
2). 解:关系是PE-PF=BH 5分
理由:连接AP,则有S△ABP-S△ACP=S△ABC,
故 AB·PE-AC·PF=AC·BH 8分
因为AB=AC,
所以PE-PF=BH 9分
3). 解:在等腰△DBC中,DB=DC 11分
∵PE⊥DB,PF⊥DC, 腰DB上高为AC.
由此可得PE+PF=AC.
在Rt△ABC中,∠A=90°,
∵tan B==,
设AC=x,则AB=2x.
从而x2+(2x)2=(45)2 12分
解得x=4(负舍),
∴PE+PF=AC=4.
∴PE+PF=4 14分
第7题图
第8题图 第9题图 第10题图
考生注意:本卷共八大题,计23小题,满分150分,考试时间120分钟.
一、选择题 (本题共10小题,每小题4分,满分40分).每一个小题都给出代号为A、B、C、D的四个结论,其中只有一个是正确的,把正确结论的代号写在题后的括号。每一小题:选对得 4分,不选、选错或选出的代号超过一个的(不论是否写在括号内)一律得0分。
1. 135. 下列运算结果是-2的是【 】
A.(-2)0 B.-|-2| C.2-1 D.-(-2)
2. 141. 据合肥市旅游局统计显示,2013年春节7天长假,合肥的景区、景点以及农家乐接待游客数量共达到265万人次,旅游总收入达到14.3亿元.其中14.3元亿用科学记数法表示是【 】
A.14.3×108元 B.1.43×108元 C.1.43×109元 D.14.3×109元
3. 147. 下列标志既是轴对称图形又是中心对称图形的是【 】
A. B. C. D.
4. 153. 下列调查适合普查的是【 】
A.调查2013年2月份合肥市场上某品牌饮料的质量
B.调查某月份长江安徽段水域的水质量情况
C.光明节能厂检测一批新型节能灯的使用寿命
D.了解某班50名学生的年龄情况
5. 159. 下列运算正确的是【 】
A.2a+3b=5ab B.2(a-b)=4a-b
C.(a+b)(a-b)=a2-b2 D.(a+b)2=a2+b2
6. 165. 为减轻用药负担,进一步改善群众的医疗条件,某品牌抗感染药氧氟沙星眼膏剂连续两次降价,由原来每支17.6元降至每支9.9元.若每次的降低率相同,则每次降低率为 【 】
A.15% B.20% C.25% D.30%
7. 171. 如图,AB是⊙O的直径,点C在⊙O上,若∠C=18°,
则∠BOC的度数是【 】
A.36° B.48° C.54° D.72°
8. 177. 二次函数y=ax2+bx+c(a≠0)的图象如图,
下列判断错误的是【 】
A.a<0 B.b<0 C.c<0 D.b2-4ac<0
9. 183. 现有半径为40 cm,圆心角为120°的一个扇形彩铁皮,
工人师傅打算剪去一部分扇形后,利用剩下的扇形铁皮制作成一个底面半径为12 cm的圆锥形工具(接缝处不重叠),那么剪去的扇形的圆心角为【 】
A.12° B.15° C.25° D.30°
答案:A
解析:设剪去的扇形的圆心角为x,则由题意得,40(120-x)180 π=24π,解得x=12°.
C两点,则下列结论:①当x>2时,y2
A.4个 B.3个 C.2个 D.1个
答案:A
解析:设P点坐标为(x,y),由y1=y2,即x=4x得x=2,x=-2(舍去),故A(2,2).由题意知,B(3,3),C(3,43),
所以BC=3-43=53,OA=22,OB=32,所以OAOB=23,S△ABC =12BC(3-2)=56,所以S△PBC=12BC(3-x)=2S△ABC
=53,即3-x=2,解得x=1,所以y=4,故P(1,4).又由图知,当x>2时,y2
11. 196. 计算:9-sin30°= .
12. 198. 如图,已知AB∥CD,若∠A=35°,∠E=20°,则∠C的度数是 .
13. 200. 电子锁的密码是一个六位数,现已知第一、三、四位上的数字分别为1、0、8(如图所示),另三个数位中的三个数字有两个2一个5,小明一次就能选出正确的密码的概率是 .
14. 202. 如图,在Rt△ABC中,AB=CB,BO⊥AC,把△ABC折叠,使AB落在AC上,点B与AC上的点E重合,展开后,折痕AD交BO于点F,连接DE、EF.下列结论:①DE=EC;②图中有三对全等三角形;③四边形BDEF是菱形;④S四边形DFOE=S△AOF,上述结论中正确的有 (把所有正确结论的序号都填上).
三、解答题 (本题共2小题,每小题8分,满分16分)
15. 205. 先化简,再求值:(3-xx+2)(x+2),其中x=-32.
答案:解:原式=3x+6-xx+2·(x+2) 2分
=2(x+3)x+2·(x+2) 4分
=2x+6. 6分
当x=-32时,
原式=2×(-32)+6=3. 8分
16. 207. 某中学全体师生参加义务植树活动,其中九年级的3个班师生的植树数量如下表:
班级 (1)班 (2)班 (3)班
植树(棵) 20
小明整理统计表时不小心把墨水滴到了其中两个班级的植树棵数上,但他知道:
①这三个班的植树总数量是77棵;
②(2)班植树数量比(3)班的多3棵;
请求出九(2)班与九(3)班的各植树是多少棵
答案:解:设(2)班植树x棵,则20+x+(x-3)=77,3分
解得x=30,4分
30-3=27(棵).6分
答:九(2)班植树30棵,九(3)班植树27棵.8分
四、解答题 (本题共2小题,每小题8分,满分16分)
17. 211. 如图,在一次课外数学实践活动中,小明站在操场的P处,他的前面分别是旗杆AB和一幢教学楼CD,点P、A、C在同一直线上,从P处测得旗杆顶部和教学楼顶部的仰角分别为45°和30°,已知AC=24 m,教学楼CD=20 m,求旗杆AB的高.(结果精确到1m,参考数据:2≈1.4,3≈1.7)
答案:解:∵CD⊥PC,∠DPC=30°,
∴tan30°=CDPC.
即33=2024+PA,
∴PA=203-24≈10(m). 5分
∵AB⊥PA,∠APB=45°,
∴∠ABP=45°.
∴AB=PA=10(m).
答:旗杆CD高是10m. 8分
18. 213. 如图,抛物线y=mx2+2mx+n经过点A(-4,0)和点B(0,3).
1). 求抛物线的解析式;
答案:∵抛物线y=mx2+2mx+n经过点A(-4,0)和点B(0,3),
∴16m-8m+n=0,n=3. 2分
解得m=-38,n=3. 3分
∴抛物线的解析式为:y=-38x2-34x+3.4分
2). 若将上述抛物线向右平移2个单位,再向下平移1个单位,求平移后抛物线的解析式.
答案:∵y=-38x2-34x+3=-38(x+1)2+278.
∴将此抛物线向右平移2个单位,再向下平移1个单位的解析式为
y=-38(x+1-2)2+278-1
即y=-38(x-1)2+198. 8分
五、解答题 (本题共2小题,每小题10分,满分20分)
19. 219. 如图,在△ABC中,DE∥BC,分别交AB、AC于点D、E,以AD、AE为边作ADFE交BC于点G,H,且EH=EC.
1). 求证:∠B=∠C;
答案: ADFE中,AD∥EF,
∵∠EHC=∠B,又∵EH=EC,
∴∠EHC=∠C,3分
∴∠B=∠C.4分
2). 求证:ADFE是菱形.
答案:∵DE∥BC,
∴∠AED=∠C,∠ADE=∠B,6分
∵∠B=∠C,∴∠AED=∠ADE.8分
∴AD=AE,
∴ ADFE是菱形.10分
20. 224. 将正整数按如图的方式,每层四个数分A、B、C、D四个方向连续地排列下去.请回答下列问题:
1). 数2013排列在什么方向上 B方向的第100个数是多少
答案:数2013排列在A方向上;B方向的第100个数是398.3分
2). 是否存在某一层上的四个数和为200 为什么
答案:设某层上的四个数分别为x,x+1,x+2,x+3,
若x+(x+1)+(x+2)+(x+3)=200,5分
解得:x=972.
∵972不是正整数,
∴不存在某一层上的四个数和为200. 7分
3). 求第n层的四个数的和(用含n的代数式表示).
答案:第n层的四个数分别是4(n-1)+1,4(n-1)+2,4(n-1)+3,4n.8分
[4(n-1)+1]+[4(n-1)+2]+[4(n-1)+3]+4n
=16n-6.
即第n层的四个数的和是16n-6. 10分
六、 解答题 (本题满分12分)
21. 233. 九年级甲、乙两位学生积极进行体育训练,并在训练期间内先后进行了五次体育测试,甲同学的测试成绩如表,乙同学的测试成绩折线统计图如图所示:
甲同学测试成绩
次数 一 二 三 四 五
分数 46 47 48 49 50
1). 请根据甲、乙两同学五次体育测试的成绩填写下表:
中位数 平均数 方差
甲 48 2
乙 48
答案:甲:平均数48 乙:中位数48 方差0.8.3分
2). 甲、乙两同学这五次测试的成绩中,谁的变化相对平缓 为什么
答案:乙同学五次体育测试成绩较平缓.因为乙的五次测试成绩的方差和极差小于甲的方差和极差.6分
3). 在图中,画出甲的测试成绩的折线图,从甲、乙两同学这五次体育测试的成绩的折线图来看,甲、乙两位同学,谁的训练成效更为显著 请说明理由.
答案:图略,甲同学的训练成效更为显著.因为甲的五次测试成绩逐步上升,并由开始低于乙的成绩逐渐上升到高于乙的成绩.12分
七、 解答题 (本题满分12分)
22. 241. A、B两座城市之间有一条高速公路,甲、乙两辆汽车同时分别从这条路两端的入口处驶入,并始终在高速公路上正常行驶.甲车驶往B城,乙车驶往A城,甲车在行驶过程中速度始终不变.甲车距B城高速公路入口处的距离y(km)与行驶时间x(h)之间的关系如图所示.
1). 求y关于x的表达式;
答案:设y=kx+b,将(0,300),(2,120)代入得:
b=300,2k+b=120,解得k=-90,b=300.2分
所以y=-90x+300.3分
2). 在两车相遇前,乙车以60 km/h的速度匀速行驶;两车相遇后,乙车改变了行车速度并保持匀速行驶,结果共用了4 h到达A城.请求出两车相遇的时间,并在图中画出乙车离开B城高速公路入口处的距离y(km)与行驶时间x(h)之间的函数图象;
答案:由图象知:甲车的速度为90 km/h,4分
设两车出发后t时相遇,则90t+60t=300,5分
t=2.
即出发后2小时两车相遇.
乙车的图象略.8分
3). 在(2)的条件下,直接写出乙车变化后的速度,并求当甲车到达B城时两车相距多少千米
答案:乙车变化后的速度为90 km/h.9分
当y=0时,由0=-90x+300,得x=103.10分
此时,乙车距B城的距离是60×2+90×(103-2)=240 (km).12分
即当甲车到达B城时两车相距240 km.
八、 解答题 (本题满分14分)
23. 250. 阅读下面的材料:
如右图所示,P是等腰△ABC的底边BC上任一点,PE⊥AB于E,PF⊥AC于F,BH是腰AC上的高,求证:PE+PF=BH.
证明:连接AP,则有S△ABC=S△ABP+S△ACP,得
12AC×BH=12AC×PF+12AB×PE.
因为AB=AC,所以BH=PE+PH.
请你利用上面的结论或方法解答下列问题:
1). 如图①,P是边长为2的正方形ABCD边AD上任意一点,且PE⊥AC于E,PF⊥DB于F,求PE+PF的值;
答案:在等腰△OAD中,OA=OD.
∵PE⊥AC,PF⊥DB,腰OA上高为OD.由题结论可得PE+PF=OD.2分
又OD=12BD=2,∴PE+PF=2.4分
2). 如图②,P是等腰△ABC的底边BC的延长线上一点,PE⊥AB于E,PF⊥AC且交AC的延长线于F,BH是腰AC上的高,那么PE,PF与BH有何数量关系 并说明理由;
答案:关系是PE-PF=BH.5分
理由:连接AP,则有S△ABP-S△ACP=S△ABC,故
12AB·PE-12AC·PF=12AC·BH.8分
因为AB=AC,所以PE-PF=BH.9分
3). 如图③,在Rt△ABC中,∠A=90°,D是AB上一点,且BD=CD,过BC上任一点P作PE⊥DB于E,PF⊥DC于F,若tan∠B=12,BC=45,求PE+PF的值.
答案:在等腰△DBC中,DB=DC.11分
∵PE⊥DB,PF⊥DC,腰DB上高为AC.由此可得PE+PF=AC.
在Rt△ABC中,∠A=90°,∵tan B=ACAB=12,
设AC=x,则AB=2x.从而x2+(2x)2=(45)2,12分
解得x=4(负舍),∴PE+PF=AC=4.∴PE+PF=4. 14分
答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 B C A D C C A B A A
二、填空题
11. 52 12. 55° 13. 14. ① ③ ④
三、
15. 解:原式=3x+6-xx+2·(x+2) 2分
=2(x+3)x+2·(x+2) 4分
=2x+6. 6分
当x=-32时,
原式=2×(-32)+6=3. 8分
16. 解:设(2)班植树x棵,则20+x+(x-3)=77 3分
解得x=30 4分
30-3=27(棵) 6分
答:九(2)班植树30棵,九(3)班植树27棵 8分
四、
17. 解:∵CD⊥PC,∠DPC=30°,
∴tan30°=CDPC.
即33=2024+PA,
∴PA=203-24≈10(m) 5分
∵AB⊥PA,∠APB=45°,
∴∠ABP=45°.
∴AB=PA=10(m).
答:旗杆CD高是10m 8分
18. 1). 解:∵抛物线y=mx2+2mx+n经过点A(-4,0)和点B(0,3),
∴16m-8m+n=0,n=3 2分
解得m=-38,n=3 3分
∴抛物线的解析式为:y=-38x2-34x+3 4分
2).解:∵y=-38x2-34x+3=-38(x+1)2+278.
∴将此抛物线向右平移2个单位,再向下平移1个单位的解析式为
y=-38(x+1-2)2+278-1
即y=-38(x-1)2+198 8分
五、
19. 1). 证明: ADFE中,AD∥EF,
∴∠EHC=∠B,
又∵EH=EC,
∴∠EHC=∠C 3分
∴∠B=∠C 4分
2). 证明:∵DE∥BC,
∴∠AED=∠C,∠ADE=∠B 6分
∵∠B=∠C,
∴∠AED=∠ADE 8分
∴AD=AE,
∴ADFE是菱形 10分
20. 1). 答:数2013排列在A方向上;B方向的第100个数是398 3分
2). 解:设某层上的四个数分别为x,x+1,x+2,x+3,
若x+(x+1)+(x+2)+(x+3)=200 5分
解得:x=.
∵不是正整数,
∴不存在某一层上的四个数和为200 7分
3). 解:第n层的四个数分别是4(n-1)+1,4(n-1)+2,4(n-1)+3,4n 8分
[4(n-1)+1]+[4(n-1)+2]+[4(n-1)+3]+4n
=16n-6.
即第n层的四个数的和是16n-6 10分
六、
21. 1). 答:甲:平均数48 乙:中位数48 方差0.8 3分
2). 答:乙同学五次体育测试成绩较平缓.因为乙的五次测试成绩的
方差和极差小于甲的方差和极差 6分
3). 答:图略,甲同学的训练成效更为显著.因为甲的五次测试成绩逐步上升,
并由开始低于乙的成绩逐渐上升到高于乙的成绩 12分
七、
22. 1). 解:设y=kx+b,将(0,300),(2,120)代入得:
解得k=-90,b=300 2分
所以y=-90x+300 3分
2). 解:由图象知:甲车的速度为90 km/h 4分
设两车出发后t时相遇,则90t+60t=300 5分
t=2.
即出发后2小时两车相遇.
乙车的图象略 8分
3). 解:乙车变化后的速度为90 km/h 9分
当y=0时,由0=-90x+300,得x=103 10分
此时,乙车距B城的距离是60×2+90×(103-2)=240 (km) 12分
即当甲车到达B城时两车相距240 km.
八、
23. 1). 解:在等腰△OAD中,OA=OD.
∵PE⊥AC,PF⊥DB, 腰OA上高为OD.
由题结论可得PE+PF=OD 2分
又OD=BD=2,
∴PE+PF=2 4分
2). 解:关系是PE-PF=BH 5分
理由:连接AP,则有S△ABP-S△ACP=S△ABC,
故 AB·PE-AC·PF=AC·BH 8分
因为AB=AC,
所以PE-PF=BH 9分
3). 解:在等腰△DBC中,DB=DC 11分
∵PE⊥DB,PF⊥DC, 腰DB上高为AC.
由此可得PE+PF=AC.
在Rt△ABC中,∠A=90°,
∵tan B==,
设AC=x,则AB=2x.
从而x2+(2x)2=(45)2 12分
解得x=4(负舍),
∴PE+PF=AC=4.
∴PE+PF=4 14分
第7题图
第8题图 第9题图 第10题图
同课章节目录
