人教版小学数学六年级下册5.2 鸽巢问题(2)课件(共17张PPT)
文档属性
| 名称 | 人教版小学数学六年级下册5.2 鸽巢问题(2)课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-23 00:00:00 | ||
图片预览



文档简介
(共17张PPT)
5.2 鸽巢问题(2)
枚举法
在实际生活中,有时数据较大,用“枚举法”就不太方便。
今天,我们将进一步学习用“假设法”解决实际问题。
小学人教版数学六年级下册精编教学PPT课件[21世纪教育]
知识点
用“抽屉原理”解决简单的实际问题
盒子里有同样大小的红球和蓝球各4个,要想摸出的球一定有2个同色的,至少要摸出几个球?
小学人教版数学六年级下册精编教学PPT课件[21世纪教育]
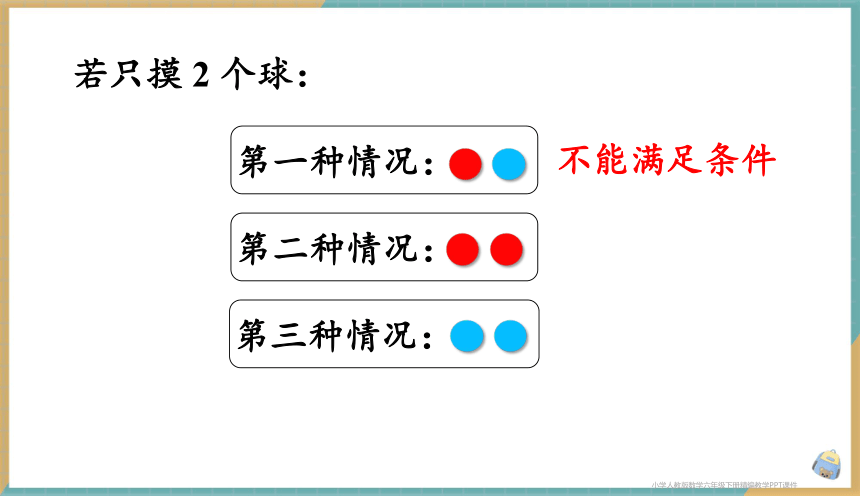
不能满足条件
若只摸 2 个球:
第一种情况:
第二种情况:
第三种情况:
小学人教版数学六年级下册精编教学PPT课件[21世纪教育]
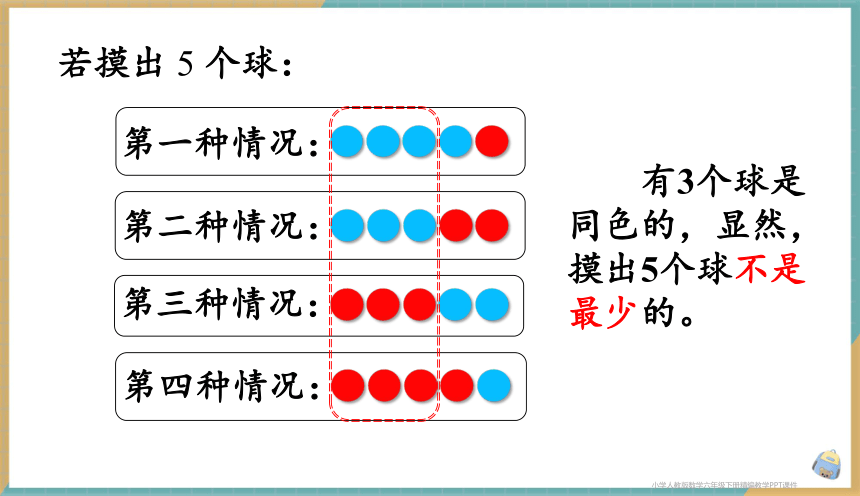
若摸出 5 个球:
有3个球是同色的,显然,摸出5个球不是最少的。
第四种情况:
第一种情况:
第二种情况:
第三种情况:
小学人教版数学六年级下册精编教学PPT课件[21世纪教育]
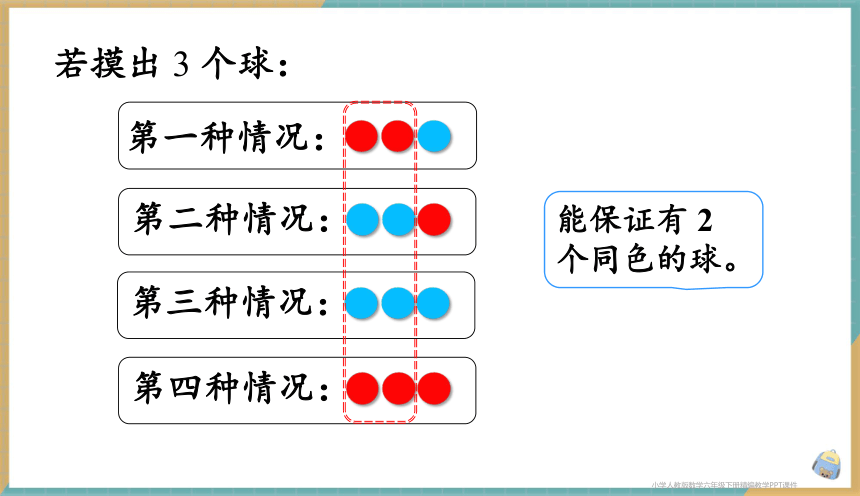
若摸出 3 个球:
能保证有 2 个同色的球。
第一种情况:
第二种情况:
第三种情况:
第四种情况:
小学人教版数学六年级下册精编教学PPT课件[21世纪教育]
只要摸出的球数比它们的颜色种数多1,就能保证有两个球同色。
至少要摸出3个球
盒子里有同样大小的红球和蓝球各4个,要想摸出的球一定有2个同色的,至少要摸出几个球?
小学人教版数学六年级下册精编教学PPT课件[21世纪教育]
用“鸽巢原理”解决求物体个数的方法:
确定把什么看作物体,把什么看作鸽巢。
确定鸽巢的个数。如果有 n 个鸽巢,要保证至少有a个物体放进同一个鸽巢,那么物体的总个数至少是(a-1)n+1。
知识提炼
小学人教版数学六年级下册精编教学PPT课件[21世纪教育]
向东小学六年级共有367名学生,其中六(2)班有37名学生。(选自教材P69做一做T1)
他说得对吗?为什么?
367÷365=1……2
1+1=2(人)
37÷12=3……1
3+1=4(人)
小试牛刀
他说得对。
小学人教版数学六年级下册精编教学PPT课件[21世纪教育]
1. 任意给出 3 个不同的自然数,其中一定有 2 个数的和是偶数,请说明理由。(选自教材P70 T4)
任意 3 个自然数有四种情况:3 个都是偶数;3 个都是奇数;1 个偶数 2 个奇数;1 个奇数 2 个偶数。也就是说必然至少有两个同为奇数或者偶数,那么这两个数相加就肯定是偶数。
小学人教版数学六年级下册精编教学PPT课件[21世纪教育]
2. 给下面每个格子涂上红色或蓝色,至少有两列的涂色方式相同。为什么?(选自教材P70 T5)
无论怎么涂,至少有两列的涂法方式相同。
小学人教版数学六年级下册精编教学PPT课件[21世纪教育]
如果只涂两行的话,结论有什么变化呢?
如果只涂两行,涂色的方式有红红、红蓝、蓝红、蓝蓝 4 种情况,
9÷4=2(列)……1(列)
2+1=3(列)
所以无论怎么涂,至少有 3 列的涂法相同。
小学人教版数学六年级下册精编教学PPT课件[21世纪教育]
3. 把43枚鸡蛋分别放进3个篮子里,总有一个篮子里。
至少放15枚鸡蛋,为什么?
43÷3=14(枚)……1(枚)
14+1=15(枚)
小学人教版数学六年级下册精编教学PPT课件[21世纪教育]
4. 把22封信投入5个信箱里,至少有5封信投入同一
个信箱里,为什么?
22÷5=4……2
4+1=5(封)
小学人教版数学六年级下册精编教学PPT课件[21世纪教育]
5. 把红、黄、蓝、白4种颜色的球各10个放到1个袋
子里。至少取多少个球,可以保证取到两个颜色相
同的球?(选自教材P69做一做T2)
把4种颜色看作4个鸽巢,每种颜色取一个正好取4个,再取 1个就可以保证取到两个颜色相同的球。
4+1=5(个)
答:至少取5个球,可以保证取到两个颜色相同的球。
小学人教版数学六年级下册精编教学PPT课件[21世纪教育]
这节课你们都学会了哪些知识?
用“鸽巢原理”解决求物体个数的方法:
确定把什么看作物体,把什么看作鸽巢。
确定鸽巢的个数。如果有 n 个鸽巢,要保证至少有a个物体放进同一个鸽巢,那么物体的总个数至少是(a-1)n+1。
小学人教版数学六年级下册精编教学PPT课件[21世纪教育]
作业1:完成教材相关练习题。
作业2:完成练习题。
小学人教版数学六年级下册精编教学PPT课件[21世纪教育]
5.2 鸽巢问题(2)
枚举法
在实际生活中,有时数据较大,用“枚举法”就不太方便。
今天,我们将进一步学习用“假设法”解决实际问题。
小学人教版数学六年级下册精编教学PPT课件[21世纪教育]
知识点
用“抽屉原理”解决简单的实际问题
盒子里有同样大小的红球和蓝球各4个,要想摸出的球一定有2个同色的,至少要摸出几个球?
小学人教版数学六年级下册精编教学PPT课件[21世纪教育]
不能满足条件
若只摸 2 个球:
第一种情况:
第二种情况:
第三种情况:
小学人教版数学六年级下册精编教学PPT课件[21世纪教育]
若摸出 5 个球:
有3个球是同色的,显然,摸出5个球不是最少的。
第四种情况:
第一种情况:
第二种情况:
第三种情况:
小学人教版数学六年级下册精编教学PPT课件[21世纪教育]
若摸出 3 个球:
能保证有 2 个同色的球。
第一种情况:
第二种情况:
第三种情况:
第四种情况:
小学人教版数学六年级下册精编教学PPT课件[21世纪教育]
只要摸出的球数比它们的颜色种数多1,就能保证有两个球同色。
至少要摸出3个球
盒子里有同样大小的红球和蓝球各4个,要想摸出的球一定有2个同色的,至少要摸出几个球?
小学人教版数学六年级下册精编教学PPT课件[21世纪教育]
用“鸽巢原理”解决求物体个数的方法:
确定把什么看作物体,把什么看作鸽巢。
确定鸽巢的个数。如果有 n 个鸽巢,要保证至少有a个物体放进同一个鸽巢,那么物体的总个数至少是(a-1)n+1。
知识提炼
小学人教版数学六年级下册精编教学PPT课件[21世纪教育]
向东小学六年级共有367名学生,其中六(2)班有37名学生。(选自教材P69做一做T1)
他说得对吗?为什么?
367÷365=1……2
1+1=2(人)
37÷12=3……1
3+1=4(人)
小试牛刀
他说得对。
小学人教版数学六年级下册精编教学PPT课件[21世纪教育]
1. 任意给出 3 个不同的自然数,其中一定有 2 个数的和是偶数,请说明理由。(选自教材P70 T4)
任意 3 个自然数有四种情况:3 个都是偶数;3 个都是奇数;1 个偶数 2 个奇数;1 个奇数 2 个偶数。也就是说必然至少有两个同为奇数或者偶数,那么这两个数相加就肯定是偶数。
小学人教版数学六年级下册精编教学PPT课件[21世纪教育]
2. 给下面每个格子涂上红色或蓝色,至少有两列的涂色方式相同。为什么?(选自教材P70 T5)
无论怎么涂,至少有两列的涂法方式相同。
小学人教版数学六年级下册精编教学PPT课件[21世纪教育]
如果只涂两行的话,结论有什么变化呢?
如果只涂两行,涂色的方式有红红、红蓝、蓝红、蓝蓝 4 种情况,
9÷4=2(列)……1(列)
2+1=3(列)
所以无论怎么涂,至少有 3 列的涂法相同。
小学人教版数学六年级下册精编教学PPT课件[21世纪教育]
3. 把43枚鸡蛋分别放进3个篮子里,总有一个篮子里。
至少放15枚鸡蛋,为什么?
43÷3=14(枚)……1(枚)
14+1=15(枚)
小学人教版数学六年级下册精编教学PPT课件[21世纪教育]
4. 把22封信投入5个信箱里,至少有5封信投入同一
个信箱里,为什么?
22÷5=4……2
4+1=5(封)
小学人教版数学六年级下册精编教学PPT课件[21世纪教育]
5. 把红、黄、蓝、白4种颜色的球各10个放到1个袋
子里。至少取多少个球,可以保证取到两个颜色相
同的球?(选自教材P69做一做T2)
把4种颜色看作4个鸽巢,每种颜色取一个正好取4个,再取 1个就可以保证取到两个颜色相同的球。
4+1=5(个)
答:至少取5个球,可以保证取到两个颜色相同的球。
小学人教版数学六年级下册精编教学PPT课件[21世纪教育]
这节课你们都学会了哪些知识?
用“鸽巢原理”解决求物体个数的方法:
确定把什么看作物体,把什么看作鸽巢。
确定鸽巢的个数。如果有 n 个鸽巢,要保证至少有a个物体放进同一个鸽巢,那么物体的总个数至少是(a-1)n+1。
小学人教版数学六年级下册精编教学PPT课件[21世纪教育]
作业1:完成教材相关练习题。
作业2:完成练习题。
小学人教版数学六年级下册精编教学PPT课件[21世纪教育]
