2023-2024学年第二学期甘肃省武威市凉州区清水镇九年制学校九年级数学人教版第二十八章《锐角三角函数》单元测试卷(含答案)
文档属性
| 名称 | 2023-2024学年第二学期甘肃省武威市凉州区清水镇九年制学校九年级数学人教版第二十八章《锐角三角函数》单元测试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 371.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-23 19:55:54 | ||
图片预览


文档简介
2023-2024学年第二学期甘肃省武威市凉州区清水镇九年制学校
九年级数学人教版第二十八章《锐角三角函数》单元测试卷
一、选择题(共30分)
1.(3分)如图,AB是圆锥的母线,BC为底面直径,已知BC=6cm,圆锥的侧面积为,则的值为( )
A. B. C. D.
2.(3分)如图,已知CD为⊙O的直径,CD⊥AB于点F,AE⊥BC于点E.若AE过圆心O,OA=1.则四边形BEOF的面积为( )
A. B. C. D.
3.(3分)如图,在矩形中,对角线、相交于点,于点,::,且,则的长度是( )
A. B. C. D.
4.(3分)一个公园的示意图如题7图所示,在大门北偏东的景点是( )
A.海洋世界 B.猴山 C.虎豹园 D.大象馆
5.(3分) 如图,△ABC的三个顶点都在方格纸的格点上,则cosA的值是( )
A. B. C. D.
6.(3分) 在中,为锐角,满足,则等于( )
A. B. C. D.
7.(3分) 在中,,,则的值为( )
A. B. C. D.
8.(3分) 2022年2月4日在北京举办了第24届冬季奥运会,很多学校都开展冰雪项目学习.如图,某滑雪斜坡的坡角为,一位同学乘滑雪板沿斜坡下滑了100米,则该同学在竖直方向上下降的高度为( )
A. B. C. D.
9.(3分)如图,在△ABC中,∠C=90°,BC=a,AC=b,AB=c,则下列选项正确的是( )
A. B. C. D.
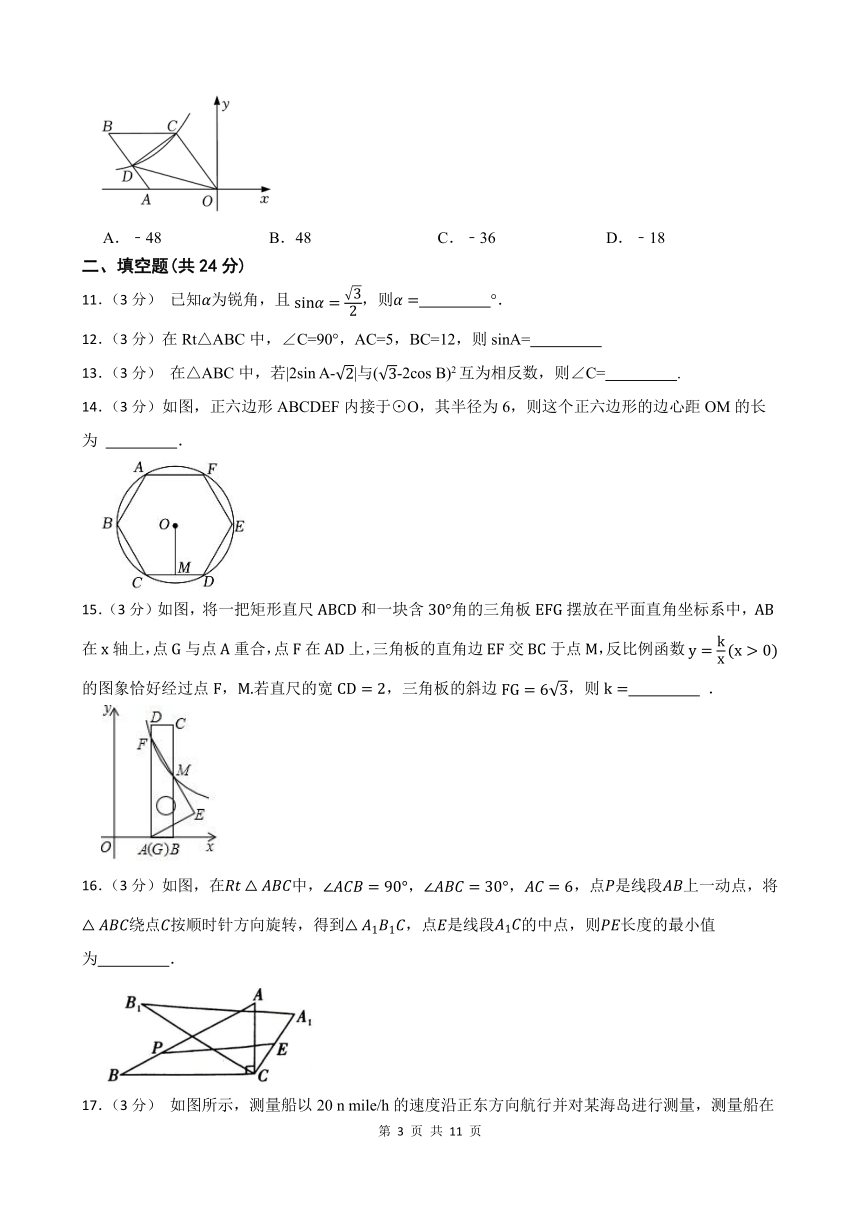
10.(3分)如图,菱形OABC的一边OA在x轴的负半轴上,O是坐标原点,tan∠AOC=,反比例函数y=的图象经过点C,与AB交于点D,若△COD的面积为30,则k的值等于( )
A.﹣48 B.48 C.﹣36 D.﹣18
二、填空题(共24分)
11.(3分) 已知为锐角,且,则 °.
12.(3分)在Rt△ABC中,∠C=90°,AC=5,BC=12,则sinA=
13.(3分) 在△ABC中,若|2sin A-|与(-2cos B)2互为相反数,则∠C= .
14.(3分)如图,正六边形ABCDEF内接于⊙O,其半径为6,则这个正六边形的边心距OM的长为 .
15.(3分)如图,将一把矩形直尺和一块含角的三角板摆放在平面直角坐标系中,在轴上,点与点重合,点在上,三角板的直角边交于点,反比例函数的图象恰好经过点,若直尺的宽,三角板的斜边,则 .
16.(3分)如图,在中,,点是线段上一动点,将绕点按顺时针方向旋转,得到,点是线段的中点,则长度的最小值为 .
17.(3分) 如图所示,测量船以20 n mile/h的速度沿正东方向航行并对某海岛进行测量,测量船在A处测得海岛上观测点D位于北偏东15°方向上,观测点C位于北偏东45°方向上,航行半个小时到达B点,这时测得海岛上观测点C位于北偏西45°方向上,若CD与AB平行,则CD= n mile(计算结果不取近似值).
18.(3分)在 ABCD中,对角线AC,BD相交于点O,若AB=4,BD=10,sin∠BDC= ,则 ABCD的面积是 .
三、计算题(共8分)
19.(1)(4分)
(2)(4分)
四、解答题(共58分)
20.(6分)先化简,再求代数式的值,其中.
21.(6分)如图,点在轴的正半轴上,抛物线与直线在第一象限内的交点为,试求的值.
22.(6分) 如图所示,AB是☉O的直径,点E是劣弧BD上一点,∠PAD=∠AED,且DE=,AE平分∠BAD,AE与BD交于点F.
(1)(3分)求证:PA是☉O的切线;
(2)(3分)若tan∠DAE=,求EF的长.
23.(6分)如图,在中,,点O为边上一点,以为半径的与相切于点D,分别交边于点E,F。
(1)(3分)求证:平分;
(2)(3分)若,求的长。
24.(8分)如图, 在 Rt 中, 是 A C 边上一点, 连接 B D, E 是 外一点且满足 平分 , 连接 D E 交 A B 于点 .
(1)(4分)求证:四边形ADBE是菱形;
(2)(4分)连接OC,若四边形ADBE的周长为20,,求 O C 的长
25.(8分)如图,航母由西向东航行,到达A处时,测得小岛C位于它的北偏东60°方向,且与航母相距80海里,再航行一段时间后到达B处,测得小岛C位于它的北偏东37°方向,如果航母继续航行至小岛C的正南方向的D处,求还需航行的距离BD的长.参考数据:sin37°≈0.6,cos37°≈0.80,tan37°≈0.75
26.(8分)楼房AB后有一假山,其坡度为i=1: ,山坡坡面上E点处有一休息亭,测得假山坡脚C与楼房水平距离BC=30米,与亭子距离CE=18米,小丽从楼房顶测得E点的俯角为45°,求楼房AB的高.
27.(10分)如图,点P在圆O外,PA与圆O相切于A点,OP与圆周相交于C点,点B与点A关于直线PO对称,已知OA=4,PA.求:
(1)(3分)∠POA的度数;
(2)(3分)弦AB的长;
(3)(4分)阴影部分的面积.
答案
1-10 BBCDD ABADC
11.60 12. 13.105° 14.3 15. 16. 17.(5-5) 18.24
19.(1)解:原式
.
(2)解:原式
20.解:
,
∵,
∴原式
21.解:当时,,
解得,舍去,
∴点的坐标为,
.
22.(1)证明:∵AB是☉O的直径,
∴∠ADB=90°.
∴∠DAB+∠DBA=90°.
∵=,∴∠AED=∠ABD.
∵∠PAD=∠AED,∴∠PAD=∠ABD.
∴∠BAD+∠PAD=∠BAD+∠ABD=90°,
即∠PAB=90°.
∴PA是☉O的切线.
(2)解:如图所示,连接OE,EB,
∵AE平分∠BAD,
∴∠DAE=∠BAE.
∴BE=DE=.
∴OE⊥BD.
∵OA=OE,
∴∠OEA=∠OAE.
∴∠DAE=∠AEO.
∴AD∥OE.
∵AB是☉O的直径,
∴∠ADF=∠BEF=90°.
∵=,∴∠DAE=∠DBE.
∴tan∠EBF=tan∠DAE=.
∴=.
∴EF=EB=1.
23.(1)证明:如图,连接.
∵是的切线,是的半径,D是切点,
∴,
∴,
∴,
∴.
∵,
∴,
∴,
∴平分;
(2)解:如图,连接,
∵在中,,,
∴,
∴.
∵是直径,
∴,
∴,
由(1)知,
∴,
∴,即,
∴.
24.(1)证明:,
四边形 A D B E 是平行四边形
∵AB平分
AE=BE
四边形ADBE是菱形.
(2)解:∵菱形ADBE的周长为20,
:.AD=BD=5,AE∥BD,
,
, 即
∴CD=3
在 Rt 中, ,
在 Rt 中, ,
,
25.解:在Rt△ADC中,∠CAD=30°,AC=80海里,
则CD=AC=×80=40(海里),
在Rt△BDC中,∠BCD=37°,
∵tan∠BCD=,
∴BD=CD tan∠BCD≈40×0.75=30(海里),
答:还需航行的距离BD的长约为30海里.
26.解:过点E作EF⊥BC的延长线于F,EH⊥AB于点H,
在Rt△CEF中,
∵i= = =tan∠ECF,∴∠ECF=30°,
∴EF= CE=9米,CF=9 米,
∴BH=EF=9米,HE=BF=BC+CF=(30+9 )米,
在Rt△AHE中,∵∠HAE=45°,
∴AH=HE=(30+9 )米,
∴AB=AH+HB=(39+9 )米.
答:楼房AB的高为(39+9 )米.
27.(1)解:∵PA是圆O的切线,切点是A.
∴OA⊥PA.
在Rt△APO中,tan∠POA,
∴∠POA=60°
(2)解:设AB与PO相交于点D,如图,
∵点B与点A关于直线PO对称,
∴AB⊥PO,且AB=2AD,
在Rt△ADO中,AD=OAsin60°=2,
∴AB=2AD=4;
(3)解:设阴影部分面积为s,
则S=S△OAP﹣S扇形AOC,
∵S△OAP=8,S扇形AOC,
∴S=8().
九年级数学人教版第二十八章《锐角三角函数》单元测试卷
一、选择题(共30分)
1.(3分)如图,AB是圆锥的母线,BC为底面直径,已知BC=6cm,圆锥的侧面积为,则的值为( )
A. B. C. D.
2.(3分)如图,已知CD为⊙O的直径,CD⊥AB于点F,AE⊥BC于点E.若AE过圆心O,OA=1.则四边形BEOF的面积为( )
A. B. C. D.
3.(3分)如图,在矩形中,对角线、相交于点,于点,::,且,则的长度是( )
A. B. C. D.
4.(3分)一个公园的示意图如题7图所示,在大门北偏东的景点是( )
A.海洋世界 B.猴山 C.虎豹园 D.大象馆
5.(3分) 如图,△ABC的三个顶点都在方格纸的格点上,则cosA的值是( )
A. B. C. D.
6.(3分) 在中,为锐角,满足,则等于( )
A. B. C. D.
7.(3分) 在中,,,则的值为( )
A. B. C. D.
8.(3分) 2022年2月4日在北京举办了第24届冬季奥运会,很多学校都开展冰雪项目学习.如图,某滑雪斜坡的坡角为,一位同学乘滑雪板沿斜坡下滑了100米,则该同学在竖直方向上下降的高度为( )
A. B. C. D.
9.(3分)如图,在△ABC中,∠C=90°,BC=a,AC=b,AB=c,则下列选项正确的是( )
A. B. C. D.
10.(3分)如图,菱形OABC的一边OA在x轴的负半轴上,O是坐标原点,tan∠AOC=,反比例函数y=的图象经过点C,与AB交于点D,若△COD的面积为30,则k的值等于( )
A.﹣48 B.48 C.﹣36 D.﹣18
二、填空题(共24分)
11.(3分) 已知为锐角,且,则 °.
12.(3分)在Rt△ABC中,∠C=90°,AC=5,BC=12,则sinA=
13.(3分) 在△ABC中,若|2sin A-|与(-2cos B)2互为相反数,则∠C= .
14.(3分)如图,正六边形ABCDEF内接于⊙O,其半径为6,则这个正六边形的边心距OM的长为 .
15.(3分)如图,将一把矩形直尺和一块含角的三角板摆放在平面直角坐标系中,在轴上,点与点重合,点在上,三角板的直角边交于点,反比例函数的图象恰好经过点,若直尺的宽,三角板的斜边,则 .
16.(3分)如图,在中,,点是线段上一动点,将绕点按顺时针方向旋转,得到,点是线段的中点,则长度的最小值为 .
17.(3分) 如图所示,测量船以20 n mile/h的速度沿正东方向航行并对某海岛进行测量,测量船在A处测得海岛上观测点D位于北偏东15°方向上,观测点C位于北偏东45°方向上,航行半个小时到达B点,这时测得海岛上观测点C位于北偏西45°方向上,若CD与AB平行,则CD= n mile(计算结果不取近似值).
18.(3分)在 ABCD中,对角线AC,BD相交于点O,若AB=4,BD=10,sin∠BDC= ,则 ABCD的面积是 .
三、计算题(共8分)
19.(1)(4分)
(2)(4分)
四、解答题(共58分)
20.(6分)先化简,再求代数式的值,其中.
21.(6分)如图,点在轴的正半轴上,抛物线与直线在第一象限内的交点为,试求的值.
22.(6分) 如图所示,AB是☉O的直径,点E是劣弧BD上一点,∠PAD=∠AED,且DE=,AE平分∠BAD,AE与BD交于点F.
(1)(3分)求证:PA是☉O的切线;
(2)(3分)若tan∠DAE=,求EF的长.
23.(6分)如图,在中,,点O为边上一点,以为半径的与相切于点D,分别交边于点E,F。
(1)(3分)求证:平分;
(2)(3分)若,求的长。
24.(8分)如图, 在 Rt 中, 是 A C 边上一点, 连接 B D, E 是 外一点且满足 平分 , 连接 D E 交 A B 于点 .
(1)(4分)求证:四边形ADBE是菱形;
(2)(4分)连接OC,若四边形ADBE的周长为20,,求 O C 的长
25.(8分)如图,航母由西向东航行,到达A处时,测得小岛C位于它的北偏东60°方向,且与航母相距80海里,再航行一段时间后到达B处,测得小岛C位于它的北偏东37°方向,如果航母继续航行至小岛C的正南方向的D处,求还需航行的距离BD的长.参考数据:sin37°≈0.6,cos37°≈0.80,tan37°≈0.75
26.(8分)楼房AB后有一假山,其坡度为i=1: ,山坡坡面上E点处有一休息亭,测得假山坡脚C与楼房水平距离BC=30米,与亭子距离CE=18米,小丽从楼房顶测得E点的俯角为45°,求楼房AB的高.
27.(10分)如图,点P在圆O外,PA与圆O相切于A点,OP与圆周相交于C点,点B与点A关于直线PO对称,已知OA=4,PA.求:
(1)(3分)∠POA的度数;
(2)(3分)弦AB的长;
(3)(4分)阴影部分的面积.
答案
1-10 BBCDD ABADC
11.60 12. 13.105° 14.3 15. 16. 17.(5-5) 18.24
19.(1)解:原式
.
(2)解:原式
20.解:
,
∵,
∴原式
21.解:当时,,
解得,舍去,
∴点的坐标为,
.
22.(1)证明:∵AB是☉O的直径,
∴∠ADB=90°.
∴∠DAB+∠DBA=90°.
∵=,∴∠AED=∠ABD.
∵∠PAD=∠AED,∴∠PAD=∠ABD.
∴∠BAD+∠PAD=∠BAD+∠ABD=90°,
即∠PAB=90°.
∴PA是☉O的切线.
(2)解:如图所示,连接OE,EB,
∵AE平分∠BAD,
∴∠DAE=∠BAE.
∴BE=DE=.
∴OE⊥BD.
∵OA=OE,
∴∠OEA=∠OAE.
∴∠DAE=∠AEO.
∴AD∥OE.
∵AB是☉O的直径,
∴∠ADF=∠BEF=90°.
∵=,∴∠DAE=∠DBE.
∴tan∠EBF=tan∠DAE=.
∴=.
∴EF=EB=1.
23.(1)证明:如图,连接.
∵是的切线,是的半径,D是切点,
∴,
∴,
∴,
∴.
∵,
∴,
∴,
∴平分;
(2)解:如图,连接,
∵在中,,,
∴,
∴.
∵是直径,
∴,
∴,
由(1)知,
∴,
∴,即,
∴.
24.(1)证明:,
四边形 A D B E 是平行四边形
∵AB平分
AE=BE
四边形ADBE是菱形.
(2)解:∵菱形ADBE的周长为20,
:.AD=BD=5,AE∥BD,
,
, 即
∴CD=3
在 Rt 中, ,
在 Rt 中, ,
,
25.解:在Rt△ADC中,∠CAD=30°,AC=80海里,
则CD=AC=×80=40(海里),
在Rt△BDC中,∠BCD=37°,
∵tan∠BCD=,
∴BD=CD tan∠BCD≈40×0.75=30(海里),
答:还需航行的距离BD的长约为30海里.
26.解:过点E作EF⊥BC的延长线于F,EH⊥AB于点H,
在Rt△CEF中,
∵i= = =tan∠ECF,∴∠ECF=30°,
∴EF= CE=9米,CF=9 米,
∴BH=EF=9米,HE=BF=BC+CF=(30+9 )米,
在Rt△AHE中,∵∠HAE=45°,
∴AH=HE=(30+9 )米,
∴AB=AH+HB=(39+9 )米.
答:楼房AB的高为(39+9 )米.
27.(1)解:∵PA是圆O的切线,切点是A.
∴OA⊥PA.
在Rt△APO中,tan∠POA,
∴∠POA=60°
(2)解:设AB与PO相交于点D,如图,
∵点B与点A关于直线PO对称,
∴AB⊥PO,且AB=2AD,
在Rt△ADO中,AD=OAsin60°=2,
∴AB=2AD=4;
(3)解:设阴影部分面积为s,
则S=S△OAP﹣S扇形AOC,
∵S△OAP=8,S扇形AOC,
∴S=8().
