六年级下册数学人教版圆柱与圆锥复习课件(共82张PPT)
文档属性
| 名称 | 六年级下册数学人教版圆柱与圆锥复习课件(共82张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 433.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-23 20:16:07 | ||
图片预览










文档简介
(共82张PPT)
圆柱圆锥复习课
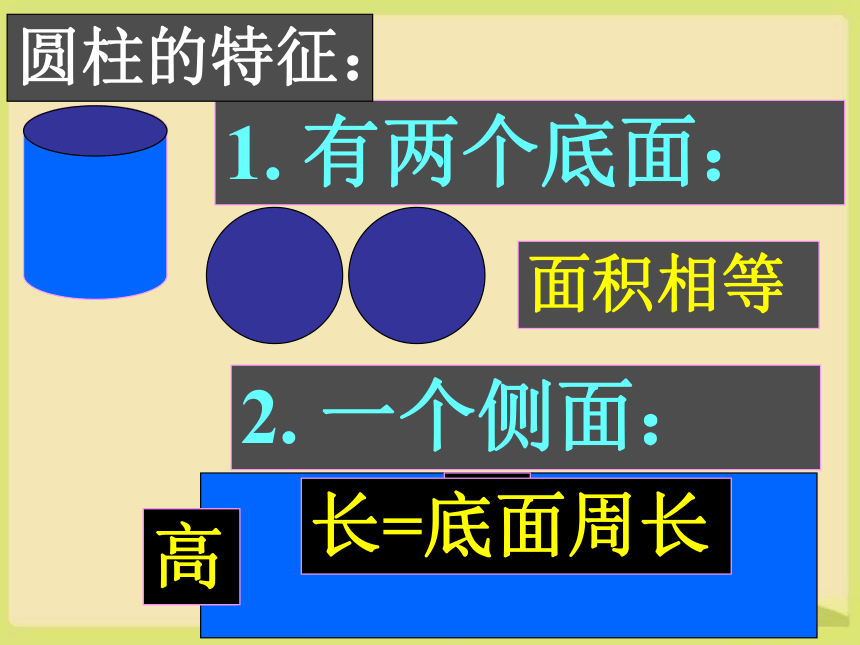
1. 有两个底面:
2. 一个侧面:
面积相等
宽
长
高
长=底面周长
圆柱的特征:
侧面积:S=底面周长×高=C×h 其中: (C=πd=2πr)
表面积:S=底面积(2个)+侧面积 其中S=πr2
注意:底面积不一定是两个!
圆柱的侧面积、表面积
圆柱的体积=底面积×高
如果已知圆柱底面的半径 r和高 h ,圆柱的体积公式是 .
V=Sh=лr2h
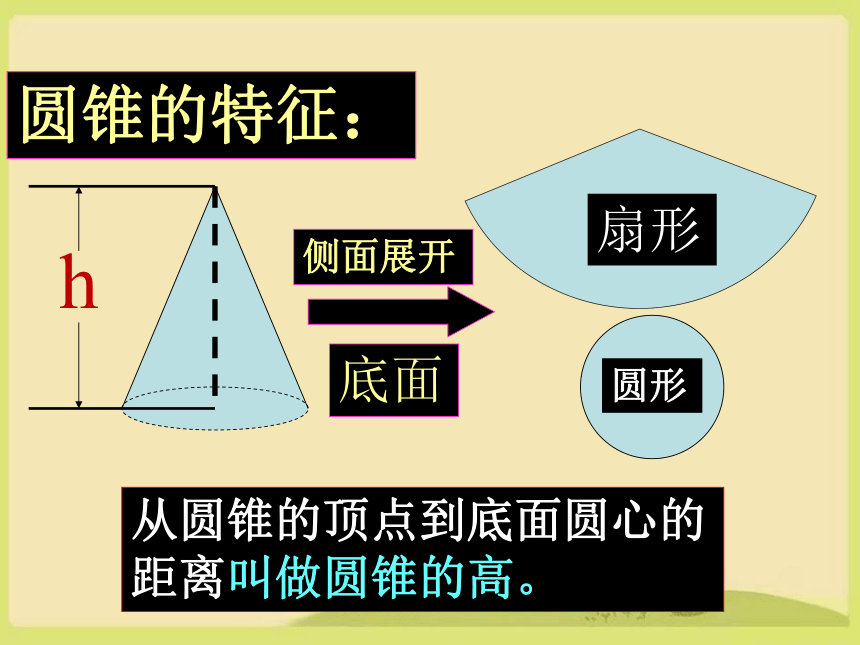
圆锥的特征:
扇形
侧面展开
底面
圆形
h
从圆锥的顶点到底面圆心的距离叫做圆锥的高。
1、已知圆锥的底面半径r和高h,如何求体积V?
S=πr2
圆锥的体积= 底面积×高
2、已知圆锥的底面直径d和高h,如何求体积V?
r= d÷2
S=πr2
圆锥的体积= 底面积×高
3、已知圆锥的底面周长C和高h,如何求体积V?
r=C÷π÷2
S=πr2
圆锥的体积= 底面积×高
圆柱
一、填空
1.把圆柱体的侧面展开,得到一个( ),它的( )等于圆柱底面周长,( )等于圆柱的高.
2. 一个圆柱体,底面周长是94.2厘米, 高是25厘米,它的侧面积是 ( )平方厘米.
长方形
长
宽
2355
3. 一个圆柱体, 底面半径是2厘米, 高是6厘米, 它的侧面积是( )平方厘米.
4. 一个圆柱体的侧面积是12.56平方厘米, 底面半径是2分米, 它的高是( )厘米.
75.36
0.1
5. 把一张长8分米, 宽5分米的白纸, 围成一个圆柱形纸筒, 这个纸筒的侧面积是( )平方分米.
6. 把一张边长为5.5厘米的正方形白纸 , 围成一个圆柱形纸筒 , 这个纸筒的侧面积是
( )平方分米.
40
0.3025
7. 圆柱体的体积等于( )乘( ),用字母表示它的计算公式是( ).
8. 把一个底面直径和高都是2分米的圆柱,切拼成一个近似的长方体,这个长方体底面的长约是( )分米,宽约是( )分米,底面积约是( )平方分米,体积约是( )立方分米.
高
底面积
V=Sh
3.14
1
3.14
6.28
把圆柱的底面平均分的份数越多,切拼成的立体图形越接近长方体。
9.一个圆柱体的底面积是105平方分米, 高是40厘米, 体积是( )立方分米.
420
二、判断
圆柱的侧面展开后一定是长方形.
( )
2. 6立方厘米比5平方厘米显然要大.
( )
3. 一个物体上、下两个面是相等的圆面,那么,它一定是圆柱形物体.
( )
×
×
×
4. 把两张相同的长方形纸,分别卷成两个形状不同的圆柱筒,并装上两个底面,那么制的圆柱的高、侧面积、表面积一定相等. ( )
5. 圆柱体的表面积=底面积×2+底面积×高. ( )
6. 圆柱体的表面积一定比它的侧面积大. ( )
7. 圆柱体的高越长,它的侧面积就越大. ( )
×
×
×
×
8.长方体、正方体、圆柱体的体积都可以用底面积乘高的方法来计算. ( )
9.圆柱体的底面积和体积成正比例. ( )
10.圆柱的体积和容积实际是一样的. ( )
√
×
×
三、求下面各圆柱体的侧面积.
1. 底面周长是6分米,高是3.5分米.
2. 底面直径是2.5分米,高是4分米.
3. 底面半径是3厘米,高是15厘米.
1. 21平方分米
2. 31.4平方分米
3. 282.6平方厘米
4.求下列圆柱的体积.
1、底面半径:8÷2=4(厘米)
底面面积:3.14×4×4=50.24(平方厘米)
圆柱体积:50.24×12=602.88(立方厘米)
答:圆柱的体积是602.88立方厘米.
2、底面半径:1.2÷2=0.6(厘米)
底面面积:3.14×0.6×0.6=1.1304(平方厘米)
圆柱体积:1.1304×0.8=0.90432(立方厘米)
答:圆柱的体积是0.90432立方厘米.
四、 选择题
1.做一个无盖的圆柱体的水桶,需要的铁皮的面积是( )
①侧面积+一个底面积
②侧面积+两个底面积
③(侧面积+底面积)×2
①
2、一个圆柱的底面直径是10厘米,高是4分米,它的侧面积是( )平方厘米.
①400 ②12.56
③125.6 ④1256
④
3、圆柱的底面直径扩大2倍,高缩小到原来的1/2 ,圆柱的侧面积是( )
①扩大2倍 ②缩小2倍 ③不变
③
五、解下列应用题.
1、一个圆柱的体积是150.72立方厘米,底面周长是12.56厘米,它的高是多少厘米?
1.底面半径:12.56÷3.14÷2=2(厘米)
底面面积:3.14×2×2=12.56(平方厘米)
高:150.72÷12.56=12(厘米)
答:它的高是12厘米.
五、解下列应用题.
2、把一根长4米的圆柱形钢材截成两段,表面积比原来增加15.7平方厘米. 这根钢材的体积是多少立方厘米?
2. 15.7÷2×4=31.4(立方厘米)
答:这根钢材的体积是31.4立方厘米.
圆锥
一、填空
1、一个圆柱和一个圆锥的底面积和高分别相等,圆锥的体积是圆柱体积的( ),圆柱的体积是圆锥体积的( ).
2、一个圆柱的体积是15立方厘米,与它等底等高的圆锥的体积是( )立方厘米.
1/3
3倍
5
3、一个圆锥的体积是7.2立方米,与它等底等高的圆柱的体积是( )立方米.
21.6
4、圆锥的底面半径是6厘米,高是20厘米,它的体积是( )立方米.
753.6
5、等底等高的圆柱和圆锥的体积相差16立方米,这个圆柱的体积是( )立方米,圆锥的体积是( )立方米.
6、等底等高的一个圆柱和一个圆锥的体积和是96立方分米,圆柱的体积是( )立方分米,圆锥的体积是( )立方分米.
24
8
72
24
7、把一个体积是18立方厘米的圆柱削成一个最大的圆锥,削成的圆锥体积是( )立方厘米.
8、一个圆柱和一个圆锥的体积和底面积相等,圆锥的高是9厘米,圆柱的高是( )厘米.
6
3
9、圆锥的底面半径是3厘米,体积是6.28立方厘米,这个圆锥的高是( )厘米.
10、一个棱长是4分米正方体容器装满水后,倒入一个底面积是12平方分米的圆锥体容器里正好装满,这个圆锥体的高是( )分米.
2/3
16
二、判断
1、圆锥的体积是等于圆柱体积的1/3.
( )
2、圆锥的体积比与它等底等高的圆柱体积小2/3. ( )
3、一个圆锥的底面半径扩大3倍,它的体积也扩大3倍. ( )
4、一个正方体和一个圆锥体的底面积和高都相等,这个正方体体积是圆锥体积的3倍. ( )
×
×
√
√
5、一个圆柱与一个圆锥的底面积和体积相等,那么圆锥的高是圆柱高的1/3 . ( )
6、把一个圆柱削成一个圆锥,这个圆锥的体积是圆柱体积的 1/3 . ( )
×
×
7、圆柱体积比与它等底等高的圆锥体的体积大2倍. ( )
8、圆锥的底面周长是12.56分米,高是4分米,它的体积是(12.56×4×1/3)立方分米.
( )
√
×
三、选择
1、一个圆柱和一个圆锥的底面直径相等,圆锥的高是圆柱的3倍,圆锥的体积是12立方分米,圆柱的体积是( )立方分米.
①12 ②36 ③4 ④8
2、一个圆锥的体积是12立方厘米,底面积是4平方厘米,高是( )厘米.
①3 ②6 ③9 ④12
①
③
3、一个圆锥的体积是n立方厘米,和它等底等高的圆柱体的体积是( )立方厘米.
① ②2n ③3n ④
③
4、把一段圆钢切削成一个最大的圆锥体,切削掉的部分部分重8千克,这段圆钢重( )千克.
①24 ②16 ③12 ④8
①
5、一个圆柱体积比一个与它等底等高的圆锥体的体积大( )
①2/3 ②1 ③2倍 ④3倍
6、一个底面直径是27厘米,高9厘米的圆锥体木块,分成形状大小完全相同的两个木块后,表面积比原来增加( )平方厘米.
①81 ②243 ③121.5 ④125.6
③
③
四、应用题
1、一堆圆锥形黄沙,底面周长是25.12米,高1.5米,每立方米的黄沙重1.5吨,这堆沙重多少吨?
1、 25.12÷3.14÷2=4(米)
1/3×(3.14×4×4)×1.5
=25.12(立方米)
1.5×25.12=37.68(吨)
答:这堆沙重37.68吨.
四、应用题
2、把一个横截面为正方形的长方体,削成一个最大的圆锥体,已知圆锥体的底面周长6.28厘米,高5厘米,长方体的体积是多少?
2、 6.28÷3.14÷2=1(厘米)
(1+1)×(1+1)×5
=20(立方厘米)
答:长方体的体积是20立方厘米.
3、一根圆柱形钢管,长30厘米,外直径是长的1/5,管壁厚1厘米,已知每立方厘米的钢重7.8克,这根钢管重多少千克?
4、一辆货车箱是一个长方体,它的长是4米,宽是1.5米,高是4米,装满一车沙,卸后沙堆成一个高是5分米的圆锥形,它的底面积是多少平方米?
3. 外直径:30×1/5 =6(厘米)
外半径:6÷2=3(厘米)
内直径:6-1-1=4(厘米)
内半径:4÷2=2(厘米)
体积:3.14×(3×3-2×2)×30
=471(立方厘米)
重量:7.8×471=3673.8(克)
答:这根钢管重3673.8克.
4.4×1.5×4÷1/3÷5=14.4(平方米)
答:它的底面积是14.4平方米.
圆柱圆锥复习课
1. 有两个底面:
2. 一个侧面:
面积相等
宽
长
高
长=底面周长
圆柱的特征:
侧面积:S=底面周长×高=C×h 其中: (C=πd=2πr)
表面积:S=底面积(2个)+侧面积 其中S=πr2
注意:底面积不一定是两个!
圆柱的侧面积、表面积
圆柱的体积=底面积×高
如果已知圆柱底面的半径 r和高 h ,圆柱的体积公式是 .
V=Sh=лr2h
圆锥的特征:
扇形
侧面展开
底面
圆形
h
从圆锥的顶点到底面圆心的距离叫做圆锥的高。
1、已知圆锥的底面半径r和高h,如何求体积V?
S=πr2
圆锥的体积= 底面积×高
2、已知圆锥的底面直径d和高h,如何求体积V?
r= d÷2
S=πr2
圆锥的体积= 底面积×高
3、已知圆锥的底面周长C和高h,如何求体积V?
r=C÷π÷2
S=πr2
圆锥的体积= 底面积×高
圆柱
一、填空
1.把圆柱体的侧面展开,得到一个( ),它的( )等于圆柱底面周长,( )等于圆柱的高.
2. 一个圆柱体,底面周长是94.2厘米, 高是25厘米,它的侧面积是 ( )平方厘米.
长方形
长
宽
2355
3. 一个圆柱体, 底面半径是2厘米, 高是6厘米, 它的侧面积是( )平方厘米.
4. 一个圆柱体的侧面积是12.56平方厘米, 底面半径是2分米, 它的高是( )厘米.
75.36
0.1
5. 把一张长8分米, 宽5分米的白纸, 围成一个圆柱形纸筒, 这个纸筒的侧面积是( )平方分米.
6. 把一张边长为5.5厘米的正方形白纸 , 围成一个圆柱形纸筒 , 这个纸筒的侧面积是
( )平方分米.
40
0.3025
7. 圆柱体的体积等于( )乘( ),用字母表示它的计算公式是( ).
8. 把一个底面直径和高都是2分米的圆柱,切拼成一个近似的长方体,这个长方体底面的长约是( )分米,宽约是( )分米,底面积约是( )平方分米,体积约是( )立方分米.
高
底面积
V=Sh
3.14
1
3.14
6.28
把圆柱的底面平均分的份数越多,切拼成的立体图形越接近长方体。
9.一个圆柱体的底面积是105平方分米, 高是40厘米, 体积是( )立方分米.
420
二、判断
圆柱的侧面展开后一定是长方形.
( )
2. 6立方厘米比5平方厘米显然要大.
( )
3. 一个物体上、下两个面是相等的圆面,那么,它一定是圆柱形物体.
( )
×
×
×
4. 把两张相同的长方形纸,分别卷成两个形状不同的圆柱筒,并装上两个底面,那么制的圆柱的高、侧面积、表面积一定相等. ( )
5. 圆柱体的表面积=底面积×2+底面积×高. ( )
6. 圆柱体的表面积一定比它的侧面积大. ( )
7. 圆柱体的高越长,它的侧面积就越大. ( )
×
×
×
×
8.长方体、正方体、圆柱体的体积都可以用底面积乘高的方法来计算. ( )
9.圆柱体的底面积和体积成正比例. ( )
10.圆柱的体积和容积实际是一样的. ( )
√
×
×
三、求下面各圆柱体的侧面积.
1. 底面周长是6分米,高是3.5分米.
2. 底面直径是2.5分米,高是4分米.
3. 底面半径是3厘米,高是15厘米.
1. 21平方分米
2. 31.4平方分米
3. 282.6平方厘米
4.求下列圆柱的体积.
1、底面半径:8÷2=4(厘米)
底面面积:3.14×4×4=50.24(平方厘米)
圆柱体积:50.24×12=602.88(立方厘米)
答:圆柱的体积是602.88立方厘米.
2、底面半径:1.2÷2=0.6(厘米)
底面面积:3.14×0.6×0.6=1.1304(平方厘米)
圆柱体积:1.1304×0.8=0.90432(立方厘米)
答:圆柱的体积是0.90432立方厘米.
四、 选择题
1.做一个无盖的圆柱体的水桶,需要的铁皮的面积是( )
①侧面积+一个底面积
②侧面积+两个底面积
③(侧面积+底面积)×2
①
2、一个圆柱的底面直径是10厘米,高是4分米,它的侧面积是( )平方厘米.
①400 ②12.56
③125.6 ④1256
④
3、圆柱的底面直径扩大2倍,高缩小到原来的1/2 ,圆柱的侧面积是( )
①扩大2倍 ②缩小2倍 ③不变
③
五、解下列应用题.
1、一个圆柱的体积是150.72立方厘米,底面周长是12.56厘米,它的高是多少厘米?
1.底面半径:12.56÷3.14÷2=2(厘米)
底面面积:3.14×2×2=12.56(平方厘米)
高:150.72÷12.56=12(厘米)
答:它的高是12厘米.
五、解下列应用题.
2、把一根长4米的圆柱形钢材截成两段,表面积比原来增加15.7平方厘米. 这根钢材的体积是多少立方厘米?
2. 15.7÷2×4=31.4(立方厘米)
答:这根钢材的体积是31.4立方厘米.
圆锥
一、填空
1、一个圆柱和一个圆锥的底面积和高分别相等,圆锥的体积是圆柱体积的( ),圆柱的体积是圆锥体积的( ).
2、一个圆柱的体积是15立方厘米,与它等底等高的圆锥的体积是( )立方厘米.
1/3
3倍
5
3、一个圆锥的体积是7.2立方米,与它等底等高的圆柱的体积是( )立方米.
21.6
4、圆锥的底面半径是6厘米,高是20厘米,它的体积是( )立方米.
753.6
5、等底等高的圆柱和圆锥的体积相差16立方米,这个圆柱的体积是( )立方米,圆锥的体积是( )立方米.
6、等底等高的一个圆柱和一个圆锥的体积和是96立方分米,圆柱的体积是( )立方分米,圆锥的体积是( )立方分米.
24
8
72
24
7、把一个体积是18立方厘米的圆柱削成一个最大的圆锥,削成的圆锥体积是( )立方厘米.
8、一个圆柱和一个圆锥的体积和底面积相等,圆锥的高是9厘米,圆柱的高是( )厘米.
6
3
9、圆锥的底面半径是3厘米,体积是6.28立方厘米,这个圆锥的高是( )厘米.
10、一个棱长是4分米正方体容器装满水后,倒入一个底面积是12平方分米的圆锥体容器里正好装满,这个圆锥体的高是( )分米.
2/3
16
二、判断
1、圆锥的体积是等于圆柱体积的1/3.
( )
2、圆锥的体积比与它等底等高的圆柱体积小2/3. ( )
3、一个圆锥的底面半径扩大3倍,它的体积也扩大3倍. ( )
4、一个正方体和一个圆锥体的底面积和高都相等,这个正方体体积是圆锥体积的3倍. ( )
×
×
√
√
5、一个圆柱与一个圆锥的底面积和体积相等,那么圆锥的高是圆柱高的1/3 . ( )
6、把一个圆柱削成一个圆锥,这个圆锥的体积是圆柱体积的 1/3 . ( )
×
×
7、圆柱体积比与它等底等高的圆锥体的体积大2倍. ( )
8、圆锥的底面周长是12.56分米,高是4分米,它的体积是(12.56×4×1/3)立方分米.
( )
√
×
三、选择
1、一个圆柱和一个圆锥的底面直径相等,圆锥的高是圆柱的3倍,圆锥的体积是12立方分米,圆柱的体积是( )立方分米.
①12 ②36 ③4 ④8
2、一个圆锥的体积是12立方厘米,底面积是4平方厘米,高是( )厘米.
①3 ②6 ③9 ④12
①
③
3、一个圆锥的体积是n立方厘米,和它等底等高的圆柱体的体积是( )立方厘米.
① ②2n ③3n ④
③
4、把一段圆钢切削成一个最大的圆锥体,切削掉的部分部分重8千克,这段圆钢重( )千克.
①24 ②16 ③12 ④8
①
5、一个圆柱体积比一个与它等底等高的圆锥体的体积大( )
①2/3 ②1 ③2倍 ④3倍
6、一个底面直径是27厘米,高9厘米的圆锥体木块,分成形状大小完全相同的两个木块后,表面积比原来增加( )平方厘米.
①81 ②243 ③121.5 ④125.6
③
③
四、应用题
1、一堆圆锥形黄沙,底面周长是25.12米,高1.5米,每立方米的黄沙重1.5吨,这堆沙重多少吨?
1、 25.12÷3.14÷2=4(米)
1/3×(3.14×4×4)×1.5
=25.12(立方米)
1.5×25.12=37.68(吨)
答:这堆沙重37.68吨.
四、应用题
2、把一个横截面为正方形的长方体,削成一个最大的圆锥体,已知圆锥体的底面周长6.28厘米,高5厘米,长方体的体积是多少?
2、 6.28÷3.14÷2=1(厘米)
(1+1)×(1+1)×5
=20(立方厘米)
答:长方体的体积是20立方厘米.
3、一根圆柱形钢管,长30厘米,外直径是长的1/5,管壁厚1厘米,已知每立方厘米的钢重7.8克,这根钢管重多少千克?
4、一辆货车箱是一个长方体,它的长是4米,宽是1.5米,高是4米,装满一车沙,卸后沙堆成一个高是5分米的圆锥形,它的底面积是多少平方米?
3. 外直径:30×1/5 =6(厘米)
外半径:6÷2=3(厘米)
内直径:6-1-1=4(厘米)
内半径:4÷2=2(厘米)
体积:3.14×(3×3-2×2)×30
=471(立方厘米)
重量:7.8×471=3673.8(克)
答:这根钢管重3673.8克.
4.4×1.5×4÷1/3÷5=14.4(平方米)
答:它的底面积是14.4平方米.
