小学数学人教版四年级下《乘法分配律》课件(共27张PPT)
文档属性
| 名称 | 小学数学人教版四年级下《乘法分配律》课件(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 798.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-23 21:51:20 | ||
图片预览






文档简介
(共27张PPT)
乘法分配律
小学数学人教版四年级下册
创设情境
矛盾激趣,引发需求
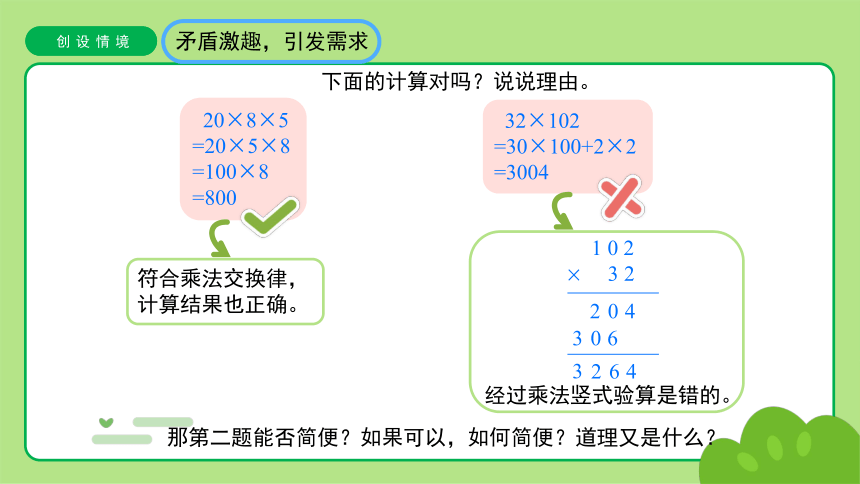
下面的计算对吗?说说理由。
20×8×5
=20×5×8
=100×8
=800
32×102
=30×100+2×2
=3004
符合乘法交换律,计算结果也正确。
4
0
1 0 2
3 2
×
2
6
0
3
4
6
2
3
经过乘法竖式验算是错的。
那第二题能否简便?如果可以,如何简便?道理又是什么?
探究新知
计算比较,初步感知
算一算:(64+36)×8,64×8+36×8。
(64+36)×8
=100×8
=800
64×8+36×8
=512+288
=800
比一比:这两个算式有哪些相同之处?有什么不同之处?
相同点:①都包含乘法和加法两种运算;
②都用到了64、36、8,且64、36在两边算式中都各出现一次。
探究新知
计算比较,初步感知
算一算:(64+36)×8,64×8+36×8。
(64+36)×8
=100×8
=800
64×8+36×8
=512+288
=800
比一比:这两个算式有哪些相同之处?有什么不同之处?
不同点:①左边算式有括号,右边算式没有;
②8在左边算式中出现一次,在右边算式中出现两次。
③左边算式先算加法,合起来以后再乘;
④右边算式分别先算乘法,再相加。
探究新知
计算比较,初步感知
算一算:(64+36)×8,64×8+36×8。
(64+36)×8
=100×8
=800
64×8+36×8
=512+288
=800
想一想:联系乘法算式的含义,想一想结果为什么相等?
因为第一个式子表示100个8,第二个式子是64个8加36个8,一共也是100个8,所以结果相等。
探究新知
计算比较,初步感知
算一算:(64+36)×8,64×8+36×8。
(64+36)×8
=100×8
=800
64×8+36×8
=512+288
=800
像这样结果相等的两个算式,就可以用等号连接写成(64+36)×8=64×8+36×8。
写一写
探究新知
问题解决,引发猜想
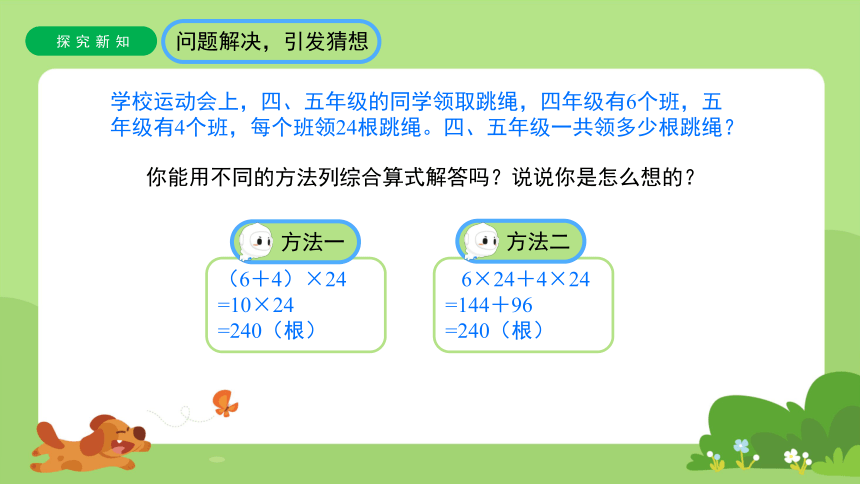
学校运动会上,四、五年级的同学领取跳绳,四年级有6个班,五年级有4个班,每个班领24根跳绳。四、五年级一共领多少根跳绳?
仔细审题,你得到了哪些信息?
四年级有6个班,五年级有4个班。
每个班领24根跳绳。
四、五年级一共领多少根跳绳?
探究新知
问题解决,引发猜想
学校运动会上,四、五年级的同学领取跳绳,四年级有6个班,五年级有4个班,每个班领24根跳绳。四、五年级一共领多少根跳绳?
你能用不同的方法列综合算式解答吗?说说你是怎么想的?
(6+4)×24
=10×24
=240(根)
6×24+4×24
=144+96
=240(根)
方法一
方法二
探究新知
问题解决,引发猜想
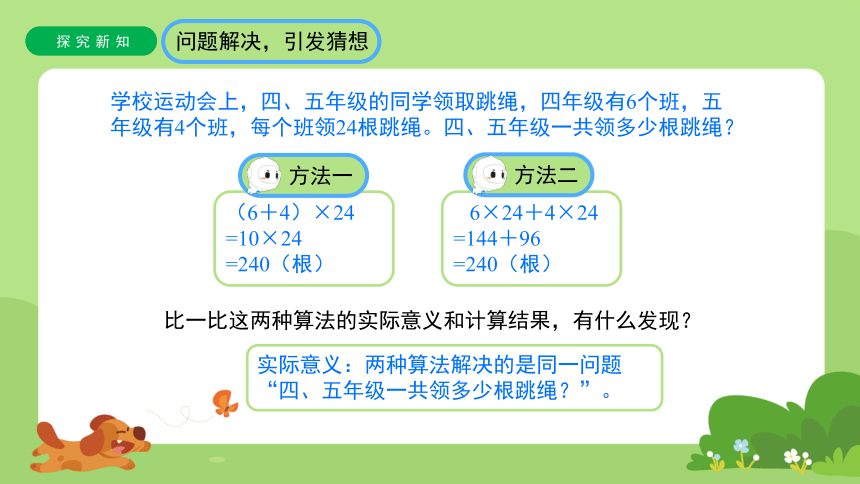
学校运动会上,四、五年级的同学领取跳绳,四年级有6个班,五年级有4个班,每个班领24根跳绳。四、五年级一共领多少根跳绳?
比一比这两种算法的实际意义和计算结果,有什么发现?
(6+4)×24
=10×24
=240(根)
6×24+4×24
=144+96
=240(根)
方法一
方法二
实际意义:两种算法解决的是同一问题“四、五年级一共领多少根跳绳?”。
探究新知
问题解决,引发猜想
学校运动会上,四、五年级的同学领取跳绳,四年级有6个班,五年级有4个班,每个班领24根跳绳。四、五年级一共领多少根跳绳?
比一比这两种算法的实际意义和计算结果,有什么发现?
(6+4)×24
=10×24
=240(根)
6×24+4×24
=144+96
=240(根)
方法一
方法二
计算结果:两种算法两个式子的计算结果相等,都是240。
探究新知
问题解决,引发猜想
学校运动会上,四、五年级的同学领取跳绳,四年级有6个班,五年级有4个班,每个班领24根跳绳。四、五年级一共领多少根跳绳?
(6+4)×24
=10×24
=240(根)
6×24+4×24
=144+96
=240(根)
方法一
方法二
像这样结果相等的两个算式,就可以用等号连接写成(6+4)×24=6×24+4×24。
小结
探究新知
数形结合,深化理解
用两种不同的方法计算长方形的周长,并结合计算过程说说它们之间的联系。
64米
26米
(64+26)×2
=90×2
=180(米)
方法一
64×2+26×2
=128+52
=180(米)
方法二
(64+26)×2=64×2+26×2
小结
探究新知
数形结合,深化理解
观察这三个等式,你有什么发现?同桌之间说一说。
(64+36)×8 = 64×8+36×8
(6+4)×24 = 6×24+4×24
(64+26)×2 = 64×2+26×2
等号右边:
这两个数先分别与第三个数相乘,再相加
等号左边:
两个数的和与一个数相乘
两个数的和与一个数相乘,可以先把它们与这个数分别相乘,再相加。
猜想
探究新知
充分验证,揭示规律
同学们提出了自己的猜想,真好。但它只是猜想显然是不够的。你们觉得还需要做些什么?
你们想用什么方法验证?
验证
可以再写几组,算一算。
可以根据乘法的意义说道理。
……
探究新知
充分验证,揭示规律
验证1:你还能再写出几组? 写一写,算一算。
(4+2)×25
=6×25
=150
4×25+2×25
=100+50
=150
(3+6)×5
=9×5
=45
3×5+6×5
=15+30
=45
(5+7)×8
=12×8
=96
5×8+7×8
=40+56
=96
……
第1组
第2组
第3组
=
=
=
探究新知
充分验证,揭示规律
验证2:根据乘法的意义,等号两边的算式分别是什么含义,说一说?
(64+36)×8 = 64×8+36×8
(6+4)×24 = 6×24+4×24
(64+26)×2 = 64×2+26×2
第一个等式:64 个 8 加上 36 个 8 就是 100 个 8 。
第二个等式:6 个 24 加上 4 个 24 就是 10 个 24 。
第三个等式:64 个 2 加上 26 个 2 就是 90 个 2 。
探究新知
充分验证,揭示规律
(64+36)×8 = 64×8+36×8
(6+4)×24 = 6×24+4×24
(64+26)×2 = 64×2+26×2
第一个等式:64 个 8 加上 36 个 8 就是 100 个 8 。
第二个等式:6 个 24 加上 4 个 24 就是 10 个 24 。
第三个等式:64 个 2 加上 26 个 2 就是 90 个 2 。
看来这样的等式并不是偶然,而是一种必然的规律,是怎样的规律呢?
探究新知
充分验证,揭示规律
(64+36)×8 = 64×8+36×8
(6+4)×24 = 6×24+4×24
(64+26)×2 = 64×2+26×2
两个数的和与一个数相乘,可以先把它们与这个数分别相乘,再相加。
规律
我们可以用字母分别表示这三个数:(a+b)×c=a×c+b×c,
这就是数学运算中一个很重要的规律:乘法分配律。
看来这样的等式并不是偶然,而是一种必然的规律,是怎样的规律呢?
探究新知
回顾反思,突出重点
回顾刚才我们探究乘法分配律的过程,经历了哪些步骤?
第一步:计算比较(64+36)×8和64× 8+36×8 ,进行初步感知;
第二步:解决问题“学校运动会上,四、五年级的同学领取跳绳,四年级有6个班,五年级有4个班,每个班领24根跳绳。四、五年级一共领多少根跳绳?”引发猜想“(6+4)×24=6×24+4×24。”
第三步:用两种不同的方法计算长方形的周长,并说明它们之间的联系,深化理解。
第四步:举例计算、根据乘法的意义说道理以验证猜想,揭示规律。
探究新知
回顾反思,突出重点
你有什么收获?
知道了什么是乘法分配律:两个数的和与一个数相乘,可以先把它们与这个数分别相乘,再相加,用字母表示是(a+b)×c=a×c+b×c。
知道了探究乘法分配律的方法。
巩固练习
分层练习,内化理解
1.结构理解:在□里填数,在○里填运算符号。
(42+35)×2=42×□+35×□
27×12+43×12=(27+□)×□
15×26+15×14=□○(□○□)
72×(30+6)=□○□○□○□
提示:根据乘法分配律填写,填的过程中,可以联系乘法算式的含义,还可以用算一算的方法检验。
2
2
43
12
15
×
26
14
+
72
×
30
+
72
×
6
巩固练习
分层练习,内化理解
2.内涵把握:下面哪些算式是正确的?正确的画“√”,错误的画“×”。
(1)(28+16)×7=28×7+16×7 ( )
(2)15×39+45×39=(15+45)×39 ( )
(3)74×(20+1)=74×20+74 ( )
(4)40×50+50×90=40×(50+90) ( )
提示:根据乘法分配律判断,判断的过程中,可以联系乘法算式的含义,还可以用算一算的方法检验。
√
√
√
×
等同于74×1,其中“1”可省略不写。
相同的因数应该在括号外
分层练习,内化理解
3.变式练习。变例题中的问题为:四年级比五年级多领多少根跳绳?
学校运动会上,四、五年级的同学领取跳绳,四年级有6个班,五年级有4个班,每个班领24根跳绳。四年级比五年级多领多少根跳绳?
如何解答这道题?
方法一:
(6-4)×24
=2×24
=48(根)
方法二:
6×24-4×24
=144-96
=48(根)
现在你对乘法分配律有什么新的认识吗?
两个数的差与一个数相乘,可以先把它们与这个数分别相乘,再相减。
乘法对减法也有分配律。
巩固练习
分层练习,内化理解
4.内化提升。小组讨论:请结合本课所学的知识,用多种方法分析说明下题的计算过程为什么是错的。
32×102
=30×100+2×2
=3004
方法一:算一算。
4
0
1 0 2
3 2
×
2
6
0
3
4
6
2
3
方法二:根据乘法的意义判断。算式含义应该是32个102,即30个102加2个102,而不是30个100加2个2。
方法三:根据乘法分配律判断。此算式不符合(a+b)×c=a×c+b×c。
巩固练习
问题解决,引发猜想
课堂小结
今天的学习你有什么收获?
矛盾激趣,引发需求
判断计算结果的正误
计算比较,初步感知
计算并比较算式
知识
内容
解决问题
用不同方法解决实际问题
用不同方法计算长方形周长
数形结合,深化理解
充分验证,揭示规律
举例
乘法分配律
拓展延伸
在□里填上适当的数。
(25+20+4)×2=□×□+□×□+□×□
123×4+9×123+2×123=□×(□+□+□)
98×5+98×6+98×3+98=□×□
根据乘法的意义,我们得出(a+b)个 c 等于 a 个 c 加上 b 个 c,即乘法分配律(a+b)×c=a×c+b×c;
其实,乘法对三个数的和、四个数的和……也有分配律,例如(a+b+c+d)个 c 等于 a 个 c 加上 b 个 c加上c个 c加上 d个 c ,所以(a+b+c+d)×c=a×c+b×c +c×c +d×c 。
25
2
20
2
4
2
123
4
9
2
98
15
提示:注意找准相同的因数;一个数与“1”相乘,可以省略“1”。
课后活动
我们探究出了乘法对加法的分配律:(a+b)×c=a×c+b×c。请你参照本节课的探究方法,探究乘法对减法的分配律: (a-b)×c=a×c-b×c。
乘法分配律
小学数学人教版四年级下册
创设情境
矛盾激趣,引发需求
下面的计算对吗?说说理由。
20×8×5
=20×5×8
=100×8
=800
32×102
=30×100+2×2
=3004
符合乘法交换律,计算结果也正确。
4
0
1 0 2
3 2
×
2
6
0
3
4
6
2
3
经过乘法竖式验算是错的。
那第二题能否简便?如果可以,如何简便?道理又是什么?
探究新知
计算比较,初步感知
算一算:(64+36)×8,64×8+36×8。
(64+36)×8
=100×8
=800
64×8+36×8
=512+288
=800
比一比:这两个算式有哪些相同之处?有什么不同之处?
相同点:①都包含乘法和加法两种运算;
②都用到了64、36、8,且64、36在两边算式中都各出现一次。
探究新知
计算比较,初步感知
算一算:(64+36)×8,64×8+36×8。
(64+36)×8
=100×8
=800
64×8+36×8
=512+288
=800
比一比:这两个算式有哪些相同之处?有什么不同之处?
不同点:①左边算式有括号,右边算式没有;
②8在左边算式中出现一次,在右边算式中出现两次。
③左边算式先算加法,合起来以后再乘;
④右边算式分别先算乘法,再相加。
探究新知
计算比较,初步感知
算一算:(64+36)×8,64×8+36×8。
(64+36)×8
=100×8
=800
64×8+36×8
=512+288
=800
想一想:联系乘法算式的含义,想一想结果为什么相等?
因为第一个式子表示100个8,第二个式子是64个8加36个8,一共也是100个8,所以结果相等。
探究新知
计算比较,初步感知
算一算:(64+36)×8,64×8+36×8。
(64+36)×8
=100×8
=800
64×8+36×8
=512+288
=800
像这样结果相等的两个算式,就可以用等号连接写成(64+36)×8=64×8+36×8。
写一写
探究新知
问题解决,引发猜想
学校运动会上,四、五年级的同学领取跳绳,四年级有6个班,五年级有4个班,每个班领24根跳绳。四、五年级一共领多少根跳绳?
仔细审题,你得到了哪些信息?
四年级有6个班,五年级有4个班。
每个班领24根跳绳。
四、五年级一共领多少根跳绳?
探究新知
问题解决,引发猜想
学校运动会上,四、五年级的同学领取跳绳,四年级有6个班,五年级有4个班,每个班领24根跳绳。四、五年级一共领多少根跳绳?
你能用不同的方法列综合算式解答吗?说说你是怎么想的?
(6+4)×24
=10×24
=240(根)
6×24+4×24
=144+96
=240(根)
方法一
方法二
探究新知
问题解决,引发猜想
学校运动会上,四、五年级的同学领取跳绳,四年级有6个班,五年级有4个班,每个班领24根跳绳。四、五年级一共领多少根跳绳?
比一比这两种算法的实际意义和计算结果,有什么发现?
(6+4)×24
=10×24
=240(根)
6×24+4×24
=144+96
=240(根)
方法一
方法二
实际意义:两种算法解决的是同一问题“四、五年级一共领多少根跳绳?”。
探究新知
问题解决,引发猜想
学校运动会上,四、五年级的同学领取跳绳,四年级有6个班,五年级有4个班,每个班领24根跳绳。四、五年级一共领多少根跳绳?
比一比这两种算法的实际意义和计算结果,有什么发现?
(6+4)×24
=10×24
=240(根)
6×24+4×24
=144+96
=240(根)
方法一
方法二
计算结果:两种算法两个式子的计算结果相等,都是240。
探究新知
问题解决,引发猜想
学校运动会上,四、五年级的同学领取跳绳,四年级有6个班,五年级有4个班,每个班领24根跳绳。四、五年级一共领多少根跳绳?
(6+4)×24
=10×24
=240(根)
6×24+4×24
=144+96
=240(根)
方法一
方法二
像这样结果相等的两个算式,就可以用等号连接写成(6+4)×24=6×24+4×24。
小结
探究新知
数形结合,深化理解
用两种不同的方法计算长方形的周长,并结合计算过程说说它们之间的联系。
64米
26米
(64+26)×2
=90×2
=180(米)
方法一
64×2+26×2
=128+52
=180(米)
方法二
(64+26)×2=64×2+26×2
小结
探究新知
数形结合,深化理解
观察这三个等式,你有什么发现?同桌之间说一说。
(64+36)×8 = 64×8+36×8
(6+4)×24 = 6×24+4×24
(64+26)×2 = 64×2+26×2
等号右边:
这两个数先分别与第三个数相乘,再相加
等号左边:
两个数的和与一个数相乘
两个数的和与一个数相乘,可以先把它们与这个数分别相乘,再相加。
猜想
探究新知
充分验证,揭示规律
同学们提出了自己的猜想,真好。但它只是猜想显然是不够的。你们觉得还需要做些什么?
你们想用什么方法验证?
验证
可以再写几组,算一算。
可以根据乘法的意义说道理。
……
探究新知
充分验证,揭示规律
验证1:你还能再写出几组? 写一写,算一算。
(4+2)×25
=6×25
=150
4×25+2×25
=100+50
=150
(3+6)×5
=9×5
=45
3×5+6×5
=15+30
=45
(5+7)×8
=12×8
=96
5×8+7×8
=40+56
=96
……
第1组
第2组
第3组
=
=
=
探究新知
充分验证,揭示规律
验证2:根据乘法的意义,等号两边的算式分别是什么含义,说一说?
(64+36)×8 = 64×8+36×8
(6+4)×24 = 6×24+4×24
(64+26)×2 = 64×2+26×2
第一个等式:64 个 8 加上 36 个 8 就是 100 个 8 。
第二个等式:6 个 24 加上 4 个 24 就是 10 个 24 。
第三个等式:64 个 2 加上 26 个 2 就是 90 个 2 。
探究新知
充分验证,揭示规律
(64+36)×8 = 64×8+36×8
(6+4)×24 = 6×24+4×24
(64+26)×2 = 64×2+26×2
第一个等式:64 个 8 加上 36 个 8 就是 100 个 8 。
第二个等式:6 个 24 加上 4 个 24 就是 10 个 24 。
第三个等式:64 个 2 加上 26 个 2 就是 90 个 2 。
看来这样的等式并不是偶然,而是一种必然的规律,是怎样的规律呢?
探究新知
充分验证,揭示规律
(64+36)×8 = 64×8+36×8
(6+4)×24 = 6×24+4×24
(64+26)×2 = 64×2+26×2
两个数的和与一个数相乘,可以先把它们与这个数分别相乘,再相加。
规律
我们可以用字母分别表示这三个数:(a+b)×c=a×c+b×c,
这就是数学运算中一个很重要的规律:乘法分配律。
看来这样的等式并不是偶然,而是一种必然的规律,是怎样的规律呢?
探究新知
回顾反思,突出重点
回顾刚才我们探究乘法分配律的过程,经历了哪些步骤?
第一步:计算比较(64+36)×8和64× 8+36×8 ,进行初步感知;
第二步:解决问题“学校运动会上,四、五年级的同学领取跳绳,四年级有6个班,五年级有4个班,每个班领24根跳绳。四、五年级一共领多少根跳绳?”引发猜想“(6+4)×24=6×24+4×24。”
第三步:用两种不同的方法计算长方形的周长,并说明它们之间的联系,深化理解。
第四步:举例计算、根据乘法的意义说道理以验证猜想,揭示规律。
探究新知
回顾反思,突出重点
你有什么收获?
知道了什么是乘法分配律:两个数的和与一个数相乘,可以先把它们与这个数分别相乘,再相加,用字母表示是(a+b)×c=a×c+b×c。
知道了探究乘法分配律的方法。
巩固练习
分层练习,内化理解
1.结构理解:在□里填数,在○里填运算符号。
(42+35)×2=42×□+35×□
27×12+43×12=(27+□)×□
15×26+15×14=□○(□○□)
72×(30+6)=□○□○□○□
提示:根据乘法分配律填写,填的过程中,可以联系乘法算式的含义,还可以用算一算的方法检验。
2
2
43
12
15
×
26
14
+
72
×
30
+
72
×
6
巩固练习
分层练习,内化理解
2.内涵把握:下面哪些算式是正确的?正确的画“√”,错误的画“×”。
(1)(28+16)×7=28×7+16×7 ( )
(2)15×39+45×39=(15+45)×39 ( )
(3)74×(20+1)=74×20+74 ( )
(4)40×50+50×90=40×(50+90) ( )
提示:根据乘法分配律判断,判断的过程中,可以联系乘法算式的含义,还可以用算一算的方法检验。
√
√
√
×
等同于74×1,其中“1”可省略不写。
相同的因数应该在括号外
分层练习,内化理解
3.变式练习。变例题中的问题为:四年级比五年级多领多少根跳绳?
学校运动会上,四、五年级的同学领取跳绳,四年级有6个班,五年级有4个班,每个班领24根跳绳。四年级比五年级多领多少根跳绳?
如何解答这道题?
方法一:
(6-4)×24
=2×24
=48(根)
方法二:
6×24-4×24
=144-96
=48(根)
现在你对乘法分配律有什么新的认识吗?
两个数的差与一个数相乘,可以先把它们与这个数分别相乘,再相减。
乘法对减法也有分配律。
巩固练习
分层练习,内化理解
4.内化提升。小组讨论:请结合本课所学的知识,用多种方法分析说明下题的计算过程为什么是错的。
32×102
=30×100+2×2
=3004
方法一:算一算。
4
0
1 0 2
3 2
×
2
6
0
3
4
6
2
3
方法二:根据乘法的意义判断。算式含义应该是32个102,即30个102加2个102,而不是30个100加2个2。
方法三:根据乘法分配律判断。此算式不符合(a+b)×c=a×c+b×c。
巩固练习
问题解决,引发猜想
课堂小结
今天的学习你有什么收获?
矛盾激趣,引发需求
判断计算结果的正误
计算比较,初步感知
计算并比较算式
知识
内容
解决问题
用不同方法解决实际问题
用不同方法计算长方形周长
数形结合,深化理解
充分验证,揭示规律
举例
乘法分配律
拓展延伸
在□里填上适当的数。
(25+20+4)×2=□×□+□×□+□×□
123×4+9×123+2×123=□×(□+□+□)
98×5+98×6+98×3+98=□×□
根据乘法的意义,我们得出(a+b)个 c 等于 a 个 c 加上 b 个 c,即乘法分配律(a+b)×c=a×c+b×c;
其实,乘法对三个数的和、四个数的和……也有分配律,例如(a+b+c+d)个 c 等于 a 个 c 加上 b 个 c加上c个 c加上 d个 c ,所以(a+b+c+d)×c=a×c+b×c +c×c +d×c 。
25
2
20
2
4
2
123
4
9
2
98
15
提示:注意找准相同的因数;一个数与“1”相乘,可以省略“1”。
课后活动
我们探究出了乘法对加法的分配律:(a+b)×c=a×c+b×c。请你参照本节课的探究方法,探究乘法对减法的分配律: (a-b)×c=a×c-b×c。
