数学人教A版(2019)选择性必修第一册3.1.1椭圆及其标准方程 课件(共21张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册3.1.1椭圆及其标准方程 课件(共21张ppt) | 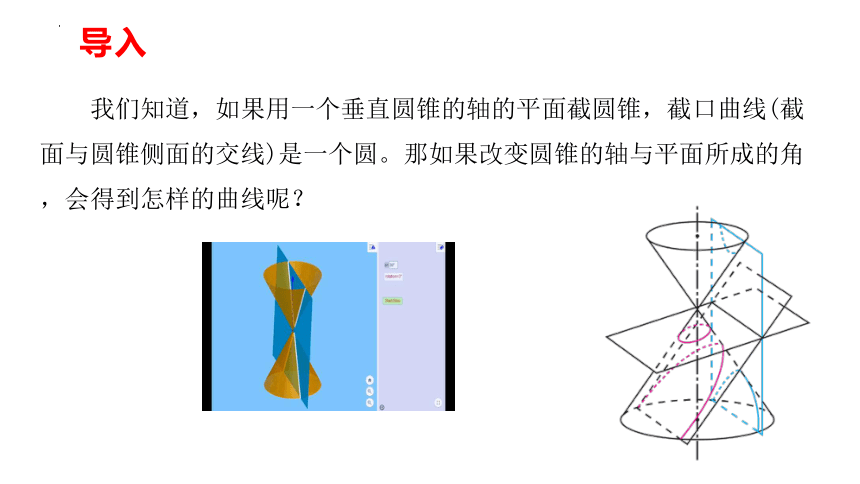 | |
| 格式 | pptx | ||
| 文件大小 | 6.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-23 19:36:36 | ||
图片预览









文档简介
(共21张PPT)
我们知道,如果用一个垂直圆锥的轴的平面截圆锥,截口曲线(截面与圆锥侧面的交线)是一个圆。那如果改变圆锥的轴与平面所成的角,会得到怎样的曲线呢?
导入
天体的运行
导入
生活中的椭圆
这么美的椭圆该如何精确地设计、制作呢?
导入
1.1 椭圆及其标准方程
1.理解椭圆的定义及椭圆的标准方程;(数学抽象)
2.掌握用定义法和待定系数法求椭圆的标准方程;(数学运算)
3.理解椭圆标准方程的推导过程,并能运用标准方程解决相关问题。(数学运算)
学习目标
探究1 椭圆的定义
圆:
O
M
r
取一条定长(没有弹性)的细绳,把它的两端都固定在画板的同一点套上铅笔拉紧绳子,移动笔尖,这时笔尖(动点)画出的轨迹是一个圆。
平面内,到定点的距离等于定长的点的集合。
新知探究
1、回忆圆的定义,说说如何画一个圆?(工具:一条细绳、一支笔)
F1
F2
2、动手画一画(小组合作)
如果把细绳的两端拉开一段距离,分别固定在画板上的两点,套上铅笔,拉紧绳子,移动笔尖,画出的轨迹是什么曲线?
问题1:
(1)在画图过程中,细绳两端是固定的还是运动的?
固定的
(2)在画图过程中,绳子长度变了没有?说明了什么?
绳子长度没变,说明M到F1和F2的距离之和是一个定值
(3)在画图过程中,绳子长度与两定点距离大小有怎样的关系?
绳子长度大于两定点的距离
M
F
2
F
1
平面内到两个定点F1、F2的距离之和等于常数(大于|F1 F2|)的点的集合(或轨迹)叫做椭圆。
这两个定点F1、F2叫做椭圆的焦点,
两焦点间的距离|F1 F2|叫做椭圆的焦距.
M
F1
F2
用2a表示
用2c表示
(2a>2c)
探究1 椭圆的定义
M
F1
F2
椭圆
线段F1F2
不存在
点的轨迹讨论
M
F1
F2
问题2:定义中的常数为什么要大于焦距|F1F2|?
F1
F2
1、求曲线方程的基本步骤:
(1)建系;(2)设点;(3)找条件;(4)列式;(5)化简;(6)验证。
2、请同学们观察椭圆形状,思考如何建系最合理 。
M
探究2 椭圆的标准方程
M
O
x
y
M
O
x
y
M
O
x
y
M
O
x
y
方案一
方案四
方案二
方案三
探究2 椭圆的标准方程
建立平面直角坐标系通常遵循的原则:对称、简洁
(1)建系:
(2)设点:
(3)列式:
x
F1
F2
M
0
y
(4)化简:
x
F1
F2
M
0
y
探究2 椭圆的标准方程
+ =1 (a>>0)
椭圆的标准方程:
它的焦点在x轴上,两个焦点分别是其中
1
o
F
y
x
2
F
M
1
2
y
o
F
F
M
x
焦点坐标: F1(-c,0)、F2(c,0)
焦点坐标: F1(0,-c )、F2(0,c)
焦点在y轴:
焦点在x轴:
探究2 椭圆的标准方程
椭圆的标准方程的再认识:
(1)椭圆标准方程的形式:左边是两个分式的平方和,右边是1;
(4)椭圆的标准方程中,x2与y2的分母哪一个大,焦点就在哪一个轴上 .
例1.用定义判断下列动点M的轨迹是否为椭圆.
(1)到F1(-2,0)、F2(2,0)的距离之和为6的点的轨迹.
(2)到F1(-2,0)、F2(2,0)的距离之和为4的点的轨迹.
(3)到F1(-2,0)、F2(2,0)的距离之和为3的点的轨迹.
是
不是椭圆,是线段|F1F2|
不是椭圆,点的轨迹不存在
新知应用
例2.请判断以下哪些方程表示椭圆,如果是,则判断焦点在哪个轴上?
指出
焦点位置的判断:
标准方程中,哪个分母大,焦点就在哪条坐标轴上!
新知应用
例3.已知椭圆的两个焦点分别为并且经过点求椭圆的标准方程。
求椭圆标准方程的步骤:
一定焦点位置;
二设椭圆方程;
三求a、b、c的值.
新知应用
(1)椭圆的定义:
我们把平面内与两个定点F1、F2的距离之和等于常数(大于|F1F2|)的点的轨迹叫做椭圆
这两个定点F1,F2叫做椭圆的焦点,两焦点间的距离|F1F2|叫做焦距。
课堂小结
标准方程中,分母哪个大,焦点就在哪个轴上!
标 准 方 程
相 同 点
焦点位置的判断
不 同 点
图 形
焦 点 坐 标
a、b、c 的关系
焦点在x轴上
焦点在y轴上
y
x
M
O
F1
F2
课堂小结
(2)椭圆的标准方程:
课后作业
、5
拓展:同步学考练
我们知道,如果用一个垂直圆锥的轴的平面截圆锥,截口曲线(截面与圆锥侧面的交线)是一个圆。那如果改变圆锥的轴与平面所成的角,会得到怎样的曲线呢?
导入
天体的运行
导入
生活中的椭圆
这么美的椭圆该如何精确地设计、制作呢?
导入
1.1 椭圆及其标准方程
1.理解椭圆的定义及椭圆的标准方程;(数学抽象)
2.掌握用定义法和待定系数法求椭圆的标准方程;(数学运算)
3.理解椭圆标准方程的推导过程,并能运用标准方程解决相关问题。(数学运算)
学习目标
探究1 椭圆的定义
圆:
O
M
r
取一条定长(没有弹性)的细绳,把它的两端都固定在画板的同一点套上铅笔拉紧绳子,移动笔尖,这时笔尖(动点)画出的轨迹是一个圆。
平面内,到定点的距离等于定长的点的集合。
新知探究
1、回忆圆的定义,说说如何画一个圆?(工具:一条细绳、一支笔)
F1
F2
2、动手画一画(小组合作)
如果把细绳的两端拉开一段距离,分别固定在画板上的两点,套上铅笔,拉紧绳子,移动笔尖,画出的轨迹是什么曲线?
问题1:
(1)在画图过程中,细绳两端是固定的还是运动的?
固定的
(2)在画图过程中,绳子长度变了没有?说明了什么?
绳子长度没变,说明M到F1和F2的距离之和是一个定值
(3)在画图过程中,绳子长度与两定点距离大小有怎样的关系?
绳子长度大于两定点的距离
M
F
2
F
1
平面内到两个定点F1、F2的距离之和等于常数(大于|F1 F2|)的点的集合(或轨迹)叫做椭圆。
这两个定点F1、F2叫做椭圆的焦点,
两焦点间的距离|F1 F2|叫做椭圆的焦距.
M
F1
F2
用2a表示
用2c表示
(2a>2c)
探究1 椭圆的定义
M
F1
F2
椭圆
线段F1F2
不存在
点的轨迹讨论
M
F1
F2
问题2:定义中的常数为什么要大于焦距|F1F2|?
F1
F2
1、求曲线方程的基本步骤:
(1)建系;(2)设点;(3)找条件;(4)列式;(5)化简;(6)验证。
2、请同学们观察椭圆形状,思考如何建系最合理 。
M
探究2 椭圆的标准方程
M
O
x
y
M
O
x
y
M
O
x
y
M
O
x
y
方案一
方案四
方案二
方案三
探究2 椭圆的标准方程
建立平面直角坐标系通常遵循的原则:对称、简洁
(1)建系:
(2)设点:
(3)列式:
x
F1
F2
M
0
y
(4)化简:
x
F1
F2
M
0
y
探究2 椭圆的标准方程
+ =1 (a>>0)
椭圆的标准方程:
它的焦点在x轴上,两个焦点分别是其中
1
o
F
y
x
2
F
M
1
2
y
o
F
F
M
x
焦点坐标: F1(-c,0)、F2(c,0)
焦点坐标: F1(0,-c )、F2(0,c)
焦点在y轴:
焦点在x轴:
探究2 椭圆的标准方程
椭圆的标准方程的再认识:
(1)椭圆标准方程的形式:左边是两个分式的平方和,右边是1;
(4)椭圆的标准方程中,x2与y2的分母哪一个大,焦点就在哪一个轴上 .
例1.用定义判断下列动点M的轨迹是否为椭圆.
(1)到F1(-2,0)、F2(2,0)的距离之和为6的点的轨迹.
(2)到F1(-2,0)、F2(2,0)的距离之和为4的点的轨迹.
(3)到F1(-2,0)、F2(2,0)的距离之和为3的点的轨迹.
是
不是椭圆,是线段|F1F2|
不是椭圆,点的轨迹不存在
新知应用
例2.请判断以下哪些方程表示椭圆,如果是,则判断焦点在哪个轴上?
指出
焦点位置的判断:
标准方程中,哪个分母大,焦点就在哪条坐标轴上!
新知应用
例3.已知椭圆的两个焦点分别为并且经过点求椭圆的标准方程。
求椭圆标准方程的步骤:
一定焦点位置;
二设椭圆方程;
三求a、b、c的值.
新知应用
(1)椭圆的定义:
我们把平面内与两个定点F1、F2的距离之和等于常数(大于|F1F2|)的点的轨迹叫做椭圆
这两个定点F1,F2叫做椭圆的焦点,两焦点间的距离|F1F2|叫做焦距。
课堂小结
标准方程中,分母哪个大,焦点就在哪个轴上!
标 准 方 程
相 同 点
焦点位置的判断
不 同 点
图 形
焦 点 坐 标
a、b、c 的关系
焦点在x轴上
焦点在y轴上
y
x
M
O
F1
F2
课堂小结
(2)椭圆的标准方程:
课后作业
、5
拓展:同步学考练
