小学数学人教版四年级下《平均数》课件(共20张PPT)
文档属性
| 名称 | 小学数学人教版四年级下《平均数》课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-23 21:49:53 | ||
图片预览





文档简介
(共20张PPT)
平均数
小学数学人教版四年级下册
创设情境
应该选哪位篮球运动员去参加全校的比赛呢
场次 第一次 第二次 第三次
个数 3 8 7
场次 第一次 第二次 第三次 第四次
个数 4 9 1 6
比较总个数
比较平均投篮的个数
比较单次投最多的个数
公平
1
2
3
探究新知
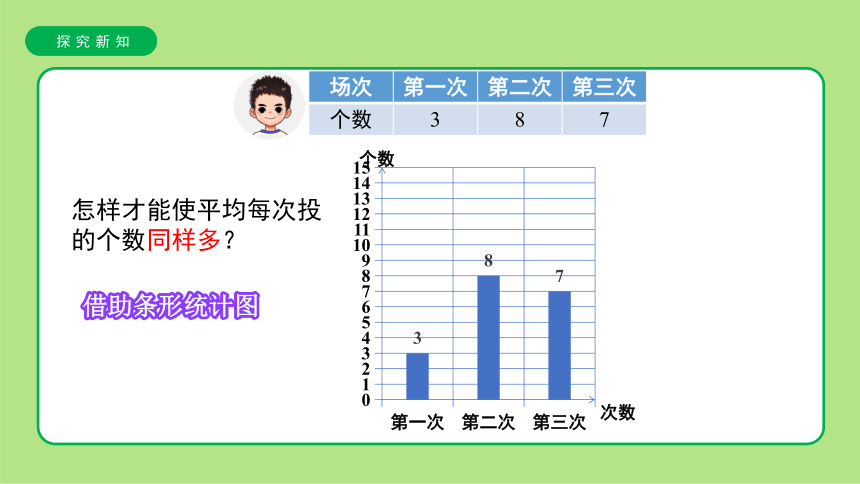
场次 第一次 第二次 第三次
个数 3 8 7
怎样才能使平均每次投的个数同样多?
借助条形统计图
借助条形统计图
探究新知
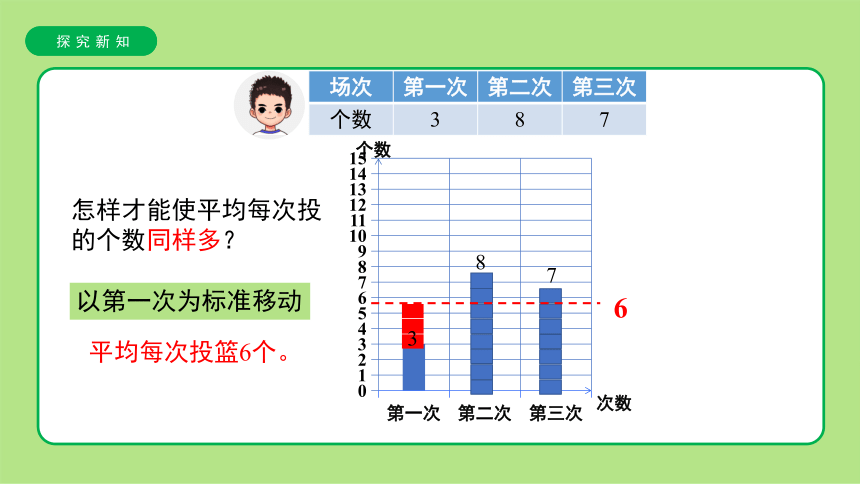
以第一次为标准移动
平均每次投篮6个。
6
场次 第一次 第二次 第三次
个数 3 8 7
怎样才能使平均每次投的个数同样多?
3
8
7
探究新知
平均每次投篮6个。
场次 第一次 第二次 第三次
个数 3 8 7
6
以第一次为标准多的拿出来再分
怎样才能使平均每次投的个数同样多?
探究新知
6是3、8、7这3个数的平均数,它反映的是这个同学3次投篮个数的整体水平。
把个数多的补给少的,最终使每次投的个数同样多
6
移多补少
移多补少
通过移多补少得到的这组同样多的数叫作这组数的 。
平均数
平均数
探究新知
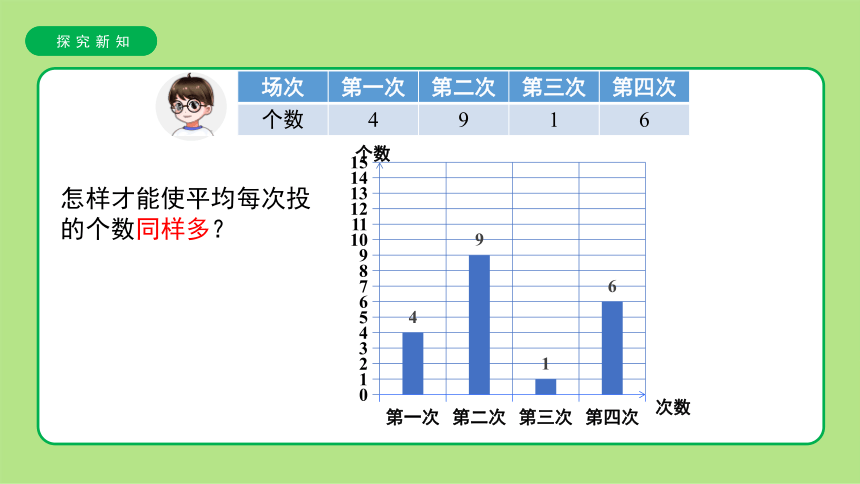
怎样才能使平均每次投的个数同样多?
场次 第一次 第二次 第三次 第四次
个数 4 9 1 6
探究新知
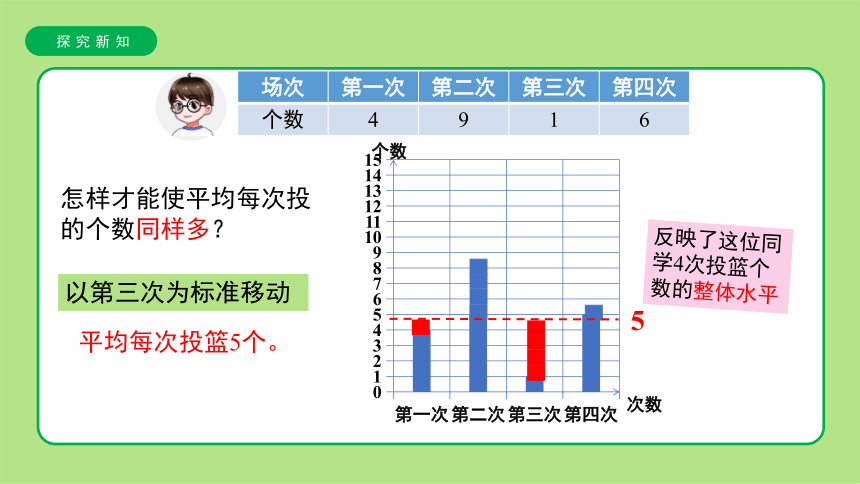
以第三次为标准移动
平均每次投篮5个。
5
反映了这位同学4次投篮个数的整体水平
怎样才能使平均每次投的个数同样多?
场次 第一次 第二次 第三次 第四次
个数 4 9 1 6
探究新知
5
6
应该选谁参加全校的比赛
探究新知
场次 第一次 第二次 第三次
个数 3 8 7
现在的平均成绩还是6个吗?
第四次
10
10
3
平均数应该在最大数和最小数之间
探究新知
(3+8+7+10)÷4=7(个)
先合并
再平均分
总数量÷总份数=平均数
7
场次 第一次 第二次 第三次
个数 3 8 7
第四次
10
怎样计算?
探究新知
场次 第一次 第二次 第三次 第四次 平均数
个数 3 8 7
10
7
(3+8+7+10)÷4=7(个)
个数 3 8 7
2
(3+8+7+2)÷4=5(个)
5
个数 3 8 7
6
(3+8+7+6)÷4=6(个)
6
观察表格,你有什么发现?
前三次的数
据没有变化
第四次数据引起平均数变化
平均数易变化
平均数易变化
7
探究新知
6
5
比较一下超过的部分与不到的部分,你发现了什么?
3=2+1
1+4=4+1
4=1+3
超出平均数的部分
超出平均数的部分
不到平均数的部分
不到平均数的部分
巩固练习
资料:摘编自《人民日报》2021年1月18日《科技视点》栏目,文字有修改。
1970年4月24日,中国发射了独
立自主研制的第一颗航天器东方红
一号卫星,迈出了走向太空的第一
步。2020年11月24日到12月17日,
嫦娥五号完成了23天的月球采样返回之旅,创造了中国航天史上又一个里程碑式的成就。从东方红一号到嫦娥五号,中国空间技术研究院研制并成功发射了300个航天器,俗称为“三百星”,包括第一颗人造卫星、第一艘飞船、第一颗导航卫星、第一颗月球探测器、第一个空间实验室、第一艘货运飞船……其中,发射第一个“百星”用了41年时间,完成第二个“百星”用了6年时间,而达成第三个“百星”只用了3年时间。
阅读资料,根据今天学均数知识,提取相关信息,提出数学问题。
1970年—2020年
300个航天器
第一个“百星”用41年
第二个“百星”用6年
第三个“百星”用3年
1970年—2020年
300个航天器
第一个“百星”用41年
第二个“百星”用6年
第三个“百星”用3年
第一个“百星”用41年,这段时间年平均发射多少颗星?
第二个“百星”用6年,这段时间年平均发射多少颗星?
50年发射300颗星,平均每年发射多少颗星?
第三个“百星”用3年,这段时间年平均发射多少颗星?
根据信息提出数学问题。
巩固练习
1
2
3
4
300÷50=6(颗)
100÷41≈2.4(颗)
100÷6≈16.7(颗)
100÷3≈33.3(颗)
总数量÷总份数=平均数
巩固练习
解决问题。
第一个“百星”用41年,这段时间每年平均发射多少颗星?
第二个“百星”用6年,这段时间每年平均发射多少颗星?
50年发射300颗星,平均每年发射多少颗星?
第三个“百星”用3年,这段时间每年平均发射多少颗星?
1
2
3
4
发射星数量 第一个百星 第二个百星 第三个百星 三百星
时间(年) 41 6 3 50
平均数 (颗/年) 2.4 16.7 33.3 6
6
你有什么发现?
与平均每年发射6颗星比较,后两个“百星”时间段内年平均发射星数量增速惊人。
每一个“百星”时间段内年平均发射星的数量成倍数增加。
第三个“百星”只用了3年时间,年平均发射33.3颗星。
我国航天事业飞速发展。
巩固练习
今天的学习你有什么收获?
今天的学习你有什么收获?
平均数
平均数的意义
平均数的求法
平均数的统计意义
课堂小结
总数量÷总份数=平均数
反映一组数据的整体水平
拓展延伸
有位同学参与了三场篮球比赛,但是老师忘记统计他的第三次成绩了,我们知道他的投篮平均个数是6,你猜猜他第三次投篮几个?
6
6×3-9-6=3(个)
想:可以根据平均数6先求出总成绩,再从总成绩里减去前两次的投篮成绩就得到第三次的成绩了。
答:第三次投篮3个。
课后活动
平均数在生活中应用十分广泛,请你列举生活中平均数应用的例子,写一写,算一算,说一说这个平均数有什么实际的意义。
平均数
小学数学人教版四年级下册
创设情境
应该选哪位篮球运动员去参加全校的比赛呢
场次 第一次 第二次 第三次
个数 3 8 7
场次 第一次 第二次 第三次 第四次
个数 4 9 1 6
比较总个数
比较平均投篮的个数
比较单次投最多的个数
公平
1
2
3
探究新知
场次 第一次 第二次 第三次
个数 3 8 7
怎样才能使平均每次投的个数同样多?
借助条形统计图
借助条形统计图
探究新知
以第一次为标准移动
平均每次投篮6个。
6
场次 第一次 第二次 第三次
个数 3 8 7
怎样才能使平均每次投的个数同样多?
3
8
7
探究新知
平均每次投篮6个。
场次 第一次 第二次 第三次
个数 3 8 7
6
以第一次为标准多的拿出来再分
怎样才能使平均每次投的个数同样多?
探究新知
6是3、8、7这3个数的平均数,它反映的是这个同学3次投篮个数的整体水平。
把个数多的补给少的,最终使每次投的个数同样多
6
移多补少
移多补少
通过移多补少得到的这组同样多的数叫作这组数的 。
平均数
平均数
探究新知
怎样才能使平均每次投的个数同样多?
场次 第一次 第二次 第三次 第四次
个数 4 9 1 6
探究新知
以第三次为标准移动
平均每次投篮5个。
5
反映了这位同学4次投篮个数的整体水平
怎样才能使平均每次投的个数同样多?
场次 第一次 第二次 第三次 第四次
个数 4 9 1 6
探究新知
5
6
应该选谁参加全校的比赛
探究新知
场次 第一次 第二次 第三次
个数 3 8 7
现在的平均成绩还是6个吗?
第四次
10
10
3
平均数应该在最大数和最小数之间
探究新知
(3+8+7+10)÷4=7(个)
先合并
再平均分
总数量÷总份数=平均数
7
场次 第一次 第二次 第三次
个数 3 8 7
第四次
10
怎样计算?
探究新知
场次 第一次 第二次 第三次 第四次 平均数
个数 3 8 7
10
7
(3+8+7+10)÷4=7(个)
个数 3 8 7
2
(3+8+7+2)÷4=5(个)
5
个数 3 8 7
6
(3+8+7+6)÷4=6(个)
6
观察表格,你有什么发现?
前三次的数
据没有变化
第四次数据引起平均数变化
平均数易变化
平均数易变化
7
探究新知
6
5
比较一下超过的部分与不到的部分,你发现了什么?
3=2+1
1+4=4+1
4=1+3
超出平均数的部分
超出平均数的部分
不到平均数的部分
不到平均数的部分
巩固练习
资料:摘编自《人民日报》2021年1月18日《科技视点》栏目,文字有修改。
1970年4月24日,中国发射了独
立自主研制的第一颗航天器东方红
一号卫星,迈出了走向太空的第一
步。2020年11月24日到12月17日,
嫦娥五号完成了23天的月球采样返回之旅,创造了中国航天史上又一个里程碑式的成就。从东方红一号到嫦娥五号,中国空间技术研究院研制并成功发射了300个航天器,俗称为“三百星”,包括第一颗人造卫星、第一艘飞船、第一颗导航卫星、第一颗月球探测器、第一个空间实验室、第一艘货运飞船……其中,发射第一个“百星”用了41年时间,完成第二个“百星”用了6年时间,而达成第三个“百星”只用了3年时间。
阅读资料,根据今天学均数知识,提取相关信息,提出数学问题。
1970年—2020年
300个航天器
第一个“百星”用41年
第二个“百星”用6年
第三个“百星”用3年
1970年—2020年
300个航天器
第一个“百星”用41年
第二个“百星”用6年
第三个“百星”用3年
第一个“百星”用41年,这段时间年平均发射多少颗星?
第二个“百星”用6年,这段时间年平均发射多少颗星?
50年发射300颗星,平均每年发射多少颗星?
第三个“百星”用3年,这段时间年平均发射多少颗星?
根据信息提出数学问题。
巩固练习
1
2
3
4
300÷50=6(颗)
100÷41≈2.4(颗)
100÷6≈16.7(颗)
100÷3≈33.3(颗)
总数量÷总份数=平均数
巩固练习
解决问题。
第一个“百星”用41年,这段时间每年平均发射多少颗星?
第二个“百星”用6年,这段时间每年平均发射多少颗星?
50年发射300颗星,平均每年发射多少颗星?
第三个“百星”用3年,这段时间每年平均发射多少颗星?
1
2
3
4
发射星数量 第一个百星 第二个百星 第三个百星 三百星
时间(年) 41 6 3 50
平均数 (颗/年) 2.4 16.7 33.3 6
6
你有什么发现?
与平均每年发射6颗星比较,后两个“百星”时间段内年平均发射星数量增速惊人。
每一个“百星”时间段内年平均发射星的数量成倍数增加。
第三个“百星”只用了3年时间,年平均发射33.3颗星。
我国航天事业飞速发展。
巩固练习
今天的学习你有什么收获?
今天的学习你有什么收获?
平均数
平均数的意义
平均数的求法
平均数的统计意义
课堂小结
总数量÷总份数=平均数
反映一组数据的整体水平
拓展延伸
有位同学参与了三场篮球比赛,但是老师忘记统计他的第三次成绩了,我们知道他的投篮平均个数是6,你猜猜他第三次投篮几个?
6
6×3-9-6=3(个)
想:可以根据平均数6先求出总成绩,再从总成绩里减去前两次的投篮成绩就得到第三次的成绩了。
答:第三次投篮3个。
课后活动
平均数在生活中应用十分广泛,请你列举生活中平均数应用的例子,写一写,算一算,说一说这个平均数有什么实际的意义。
