北师大版八年级下册 第2章 一元一次不等式与一元一次不等式组 单元测试卷(含解析)
文档属性
| 名称 | 北师大版八年级下册 第2章 一元一次不等式与一元一次不等式组 单元测试卷(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 277.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-23 00:00:00 | ||
图片预览




文档简介
北师大版八年级下册 第2章 一元一次不等式与一元一次不等式组 单元测试卷
满分120分
一.选择题(共10小题,满分30分,每小题3分)
1.在下列式子中:①﹣2<0;②a=3;③x+2>x+1;④2a+3;⑤x≠﹣2;⑥4x+5>0,是不等式的有( )
A.2个 B.3个 C.4个 D.5个
2.若a>b,则下列不等式成立的是( )
A.a﹣3<b﹣3 B.﹣2a>﹣2b C.a﹣b>0 D.
3.下列各式不是一元一次不等式组的是( )
A. B. C. D.
4.不等式x>4的解集在数轴上表示正确的是( )
A. B.
C. D.
5.已知点A(a﹣2,2a+6)在第二象限,则a的取值范围是( )
A.a<﹣3或a>2 B.﹣3<a<2 C.a<2 D.a>﹣3
6.把不等式组的解集表示在数轴上,正确的是( )
A. B.
C. D.
7.近日,教育部正式印发《义务教育课程方案》,将劳动从原来的综合实践活动课程中完全独立出来,并在今年9月份开学开始正式施行.某学校组织八年级同学到劳动教育基地参加实践活动,某小组的任务是平整土地300m2.开始的半小时,由于操作不熟练,只平整完30m2,学校要求完成全部任务的时间不超过3小时,若他们在剩余时间内每小时平整土地x m2,则x满足的不等关系为( )
A.30+(3﹣0.5)x≤300 B.300﹣30x﹣0.5≤3
C.30+(3﹣0.5)x≥300 D.0.5+300﹣30x≥3
8.已知一次函数y=kx+b(k≠0)的图象如图所示,则不等式kx+b≤0的解集是( )
A.x≤2 B.x<2 C.x≥2 D.x>2
9.不等式组的解集是x>2,则m的取值范围是( )
A.m≤2 B.m≥2 C.m≤1 D.m>1
10.若关于x的不等式组的整数解共有3个,则m的取值范围是( )
A.6<m<7 B.6≤m<7 C.6<m≤7 D.6≤m≤7
二.填空题(共8小题,满分32分,每小题4分)
11.“x的2倍与1的差比y小”用不等式表示为 .
12.选择适当的不等号填空:若a<b,则﹣2a ﹣2b.
13.若(m﹣2)x|m|﹣1>5是关于x的一元一次不等式,则m的值为 .
14.已知关于x的不等式的解集在数轴上表示如图所示,则这个不等式的解集是 .
15.不等式2x+11>0的负整数解有 个.
16.如图,直线y=kx+b经过点A(﹣2,﹣1)和B两点,则不等式x<kx+b的解集为 .
17.若关于x的不等式组无解,则m的取值范围是 .
18.若关于x的方程5(2﹣x)+x=ax的解为正数,且关于x的不等式组有解,则满足条件的所有整数a的值之和是 .
三.解答题(共7小题,满分58分)
19.(7分)解不等式2x﹣3<,并把它的解集在数轴上表示出来.
20.(7分)求不等式 的正整数解.
21.(7分)解不等式组并把解集在数轴上表示出来.
22.(8分)解不等式组,并写出满足条件的正整数解.
23.(8分)已知关于x,y的方程组的解x+y>0,则m的取值范围是多少?
24.(9分)“人间烟火气,最抚凡人心.”在这喧嚣的世界里,地摊的存在,让人们感受到了那份朴实无华的温暖,也让城市多了一份生活的温度.某个体户购买了腊梅,百合两种鲜花摆摊销售,若购进腊梅5束,百合3束,需要114元;若购进腊梅8束,百合6束,需要204元.
(1)求腊梅,百合两种鲜花的进价分别是每束多少元?
(2)若每束腊梅的售价为20元,每束百合的售价为30元.结合市场需求,该个体户决定购进两种鲜花共80束,计划购买成本不超过1260元,且购进百合的数量不少于腊梅数量的.两种鲜花全部销售完时,求销售的最大利润及相应的进货方案.
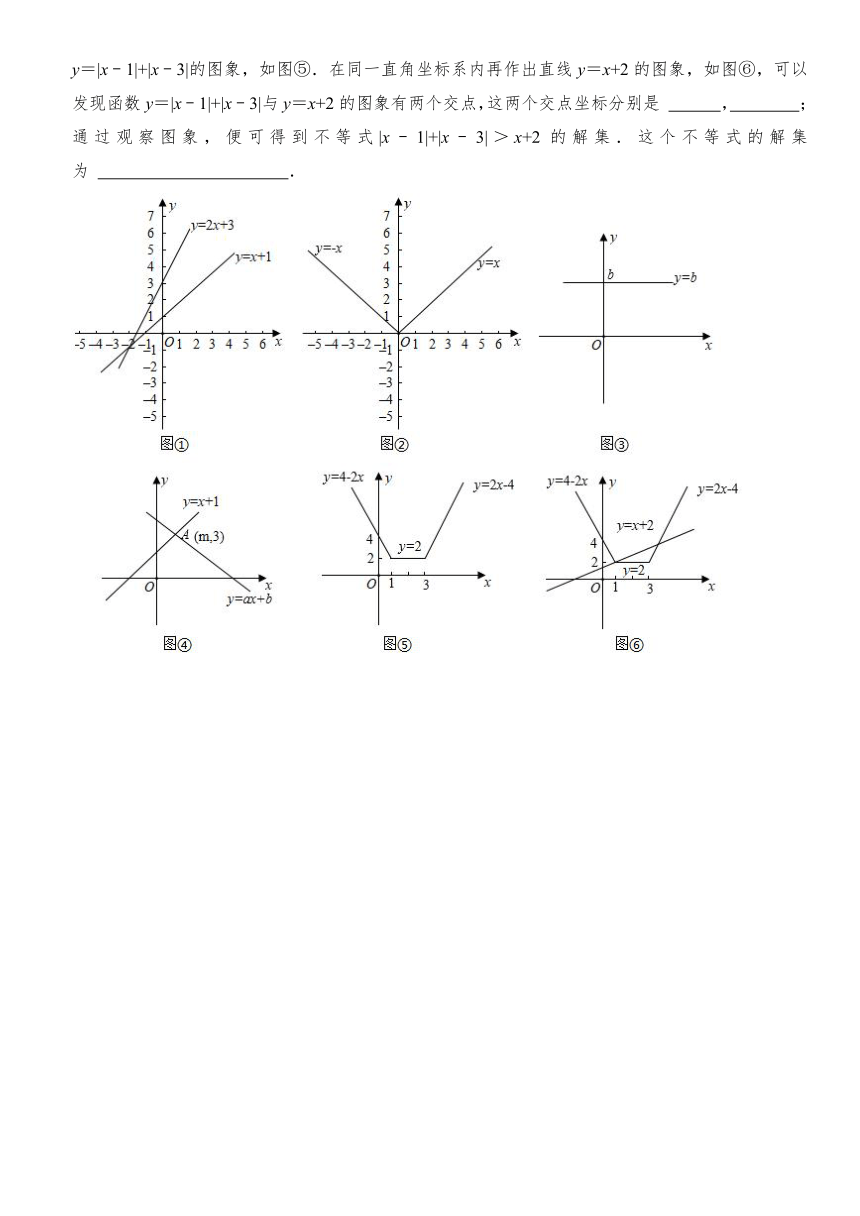
25.(12分)[问题提出]:如何解不等式|x﹣1|+|x﹣3|>x+2?
预备知识1:同学们学习了一元一次方程、一元一次不等式和一次函数,利用这些一次模型和函数的图象,可以解决一系列问题.
图①中给出了函数y=x+1和y=2x+3的图象,观察图象,我们可以得到:
当x>﹣2时,函数y=2x+3的图象在y=x+1图象上方,由此可知:不等式2x+3>x+1的解集为 .
预备知识2:函数y=|x|=,称为分段函数,其图象如图②所示,实际上对带有绝对值
的代数式的化简,通常采用“零点分段”的办法,将带有绝对值符号的代数式在各“取值段”化简,即可去掉绝对值符号.比如化简|x﹣1|+|x﹣3|时,可令x﹣1=0和x﹣3=0,分别求得x=1,x=3(称1,3分别是|x﹣1|和|x﹣3|的零点值),这样可以就x<1,1≤x<3,x≥3三种情况进行讨论:
(1)当x<1时,|x﹣1|+|x﹣3|=﹣(x﹣1)﹣(x﹣3)
(2)当1≤x<3时,|x﹣1|+|x﹣3|=(x﹣1)﹣(x﹣3)=2;
(3)当x≥3时,|x﹣1|+|x﹣3|=(x﹣1)+(x﹣3)=2x﹣4
所以|x﹣1+|x﹣3|就可以化简为
预备知识3:函数y=b(b为常数)称为常数函数,其图象如图③所示.
[知识迁移]
如图④,直线y=x+1与直线y=ax+b相交于点A(m,3),则关于x的不等式x+1≤ax+b的解集是 .
[问题解决]:
结合前面的预备知识,我们来研究怎样解不等式|x﹣1|+x﹣3|>x+2.在平面直角坐标系内作出函数y=|x﹣1|+|x﹣3|的图象,如图⑤.在同一直角坐标系内再作出直线y=x+2的图象,如图⑥,可以发现函数y=|x﹣1|+|x﹣3|与y=x+2的图象有两个交点,这两个交点坐标分别是 , ;
通过观察图象,便可得到不等式|x﹣1|+|x﹣3|>x+2的解集.这个不等式的解集为 .
参考答案
一.选择题(共10小题,满分30分,每小题3分)
1.解:不等式有:﹣2<0,x+2>x+1,x≠﹣2,4x+5>0,共4个,
故选:C.
2.解:若a>b,两边同时减3得a﹣3>b﹣3,则A不符合题意;
若a>b,两边同时乘﹣2得﹣2a<﹣2b,则B不符合题意;
若a>b,两边同时减b得a﹣b>0,则C符合题意;
若a>b,两边同时除以4得>,则D不符合题意;
故选:C.
3.解:A、该不等式组符合一元一次不等式组的定义,故本选项错误;
B、该不等式组中含有2给未知数,不是一元一次不等式组,故本选项正确;
C、该不等式组符合一元一次不等式组的定义,故本选项错误;
D、该不等式组符合一元一次不等式组的定义,故本选项错误;
故选:B.
4.解:不等式x>4的解集在数轴上表示,
故选:D.
5.解:由题意知,,
解得﹣3<a<2,
故选:B.
6.解:解不等式x+2>1,得:x>﹣1,
解不等式,得:x≤2,
则不等式组的解集为﹣1<x≤2,
在数轴上表示为:
故选:B.
7.解:依题意得:30+(3﹣0.5)x≥300.
故选:C.
8.解:由图象可得:当x≤2时,kx+b≤0,
所以不等式kx+b≤0的解集为x≤2,
故选:A.
9.解:∵不等式组的解集是x>2,
解不等式①得x>2,
解不等式②得x>m+1,
不等式组的解集是x>2,
∴不等式,①解集是不等式组的解集,
∴m+1≤2,
m≤1,
故选:C.
10.解:,
由①得,x≤m,
由②得,x>3,
故原不等式组的解集为:3<x≤m,
∵不等式组的整数解有3个,
∴其整数解应为:4、5、6,
∴m的取值范围是6≤m<7.
故选:B.
二.填空题(共8小题,满分32分,每小题4分)
11.解:依题意得2x﹣1<y,
故答案为:2x﹣1<y.
12.解:∵a<b,
∴﹣2a>﹣2b,
故答案为:>.
13.解:(m﹣2)x|m|﹣1>5是关于x的一元一次不等式,
由一元一次不等式的定义可得:m﹣2≠0且|m|﹣1=1.
解m﹣2≠0,得m≠2,
由|m|﹣1=1,得m=±2,
所以m=﹣2.
故答案为:m=﹣2.
14.解:这个不等式的解集是:x≥1.
故答案为:x≥1.
15.解:2x+11>0,
2x>﹣11,
x>﹣5.5,
所以不等式2x+11>0的负整数解有﹣5,﹣4,﹣3,﹣2,﹣1共5个,
故答案为:5.
16.解:不等式x<kx+b的解集为x<﹣2.
故答案为x<﹣2.
17.解:,
解不等式①得:x≤m+2,
解不等式②得:x>5,
∵关于x的不等式组无解,
∴m+2≤5,
解得:m≤3.
故答案为:m≤3.
18.解:5(2﹣x)+x=ax,
去括号:10﹣5x+x=ax,
移项:(a+4)x=10,
解得:x=,
∵关于x的方程5(2﹣x)+x=ax的解为正数,
∴a+4>0,
解得a>﹣4,
,
解不等式①得:x<1,
解不等式②得:x≥a,
∵不等式组有解,
∴a<1,
∴﹣4<a<1,
∴整数为﹣3或﹣2或﹣1或0,其和为﹣3+(﹣2)+(﹣1)+0=﹣6.
故答案为:﹣6.
三.解答题(共7小题,满分58分)
19.解:先去分母,得3(2x﹣3)<x﹣4,
去括号,得6x﹣9<x﹣4,
移项合并同类项,得5x<5,
系数化为1,得x<1
∴原不等式的解集为:x<1.
在数轴上表示为:
20.解:,
3(2x﹣5)≤7﹣2(x+3),
6x﹣15≤7﹣2x﹣6,
6x+2x≤7﹣6+15,
8x≤16,
x≤2,
∴该不等式的正整数解为:1,2.
21.解:解不等式①,得:x≥﹣2,
解不等式②,得:x<1,
则不等式组的解集为﹣2≤x<1,
将不等式组的解集表示在数轴上如下:
22.解:解不等式1﹣x<2(x+3),得:x>﹣1,
解不等式≥x+,得:x≤2,
∴不等式组的解集为﹣1<x≤2,
则不等式组的正整数解为1,2.
23.解:,
②×2﹣①,得x=2m﹣6,
把x=2m﹣6代入②得4m﹣12+y=m﹣1,
∴y=﹣3m+11,
∴x+y=5﹣m,
∵x+y>0,
∴5﹣m>0
∴m<5.
24.解:(1)设腊梅的进价是x元/束,百合的进价是y元/束,
根据题意得:,
解得:.
答:腊梅的进价是12元/束,百合的进价是18元/束;
(2)设购进腊梅m束,则购进百合(80﹣m)束,
根据题意得:,
解得:30≤m≤48,
设购进的两种鲜花全部销售完后获得的总利润为w元,则w=(20﹣12)m+(30﹣18)(80﹣m),
即w=﹣4m+960,
∵﹣4<0,
∴w随m的增大而减小,
∴当m=30时,w取得最小值,最小值=﹣4×30+960=840(元),此时80﹣m=80﹣30=50(束).
答:当购进腊梅30束,百合50束时,销售利润最大,销售的最大利润为840元.
25.解:[问题提出],如图,
∵当>﹣2时,函数y=2x+3的图象在y=x+1的图象上方,
∴不等式2x+3>x+1的解集为:x>﹣2,
故答案为:x>﹣2;
[知识迁移],如图,
∵点A(m,3)在y=x+1上,
∴m+1=3,
解得:m=2,
∴A(2,3),
∵当x≤2时,直线y=ax+b的图象在y=x+1的图象的上方,
∴不等式ax+b≥x+1,
即x+1≤ax+b的解集为:x≤2,
故答案为:x≤2;
[问题解决],如图,
设y=|x﹣1|+|x﹣3|,
根据题意得:
y=|x﹣1|+|x﹣3|=,
由函数图象得:
y=4﹣2x与y=x+2有交点,
则,
解得:,
y=2x﹣4与y=x+2有交点,
则,
解得:,
∴y=|x﹣1|+|x﹣3|与y=x+2的两个交点坐标分别为:();(6,8),
故答案为:();(6,8);
由函数图象可知,当x时,y=|x﹣1|+|x﹣3|的图象在y=x+2的上方,
当x>6时,y=|x﹣1|+|x﹣3|的图象在y=x+2的上方,
故不等式|x﹣1|+|x﹣3|>x+2的解集为:x或x>6,
故答案为:x或x>6.
满分120分
一.选择题(共10小题,满分30分,每小题3分)
1.在下列式子中:①﹣2<0;②a=3;③x+2>x+1;④2a+3;⑤x≠﹣2;⑥4x+5>0,是不等式的有( )
A.2个 B.3个 C.4个 D.5个
2.若a>b,则下列不等式成立的是( )
A.a﹣3<b﹣3 B.﹣2a>﹣2b C.a﹣b>0 D.
3.下列各式不是一元一次不等式组的是( )
A. B. C. D.
4.不等式x>4的解集在数轴上表示正确的是( )
A. B.
C. D.
5.已知点A(a﹣2,2a+6)在第二象限,则a的取值范围是( )
A.a<﹣3或a>2 B.﹣3<a<2 C.a<2 D.a>﹣3
6.把不等式组的解集表示在数轴上,正确的是( )
A. B.
C. D.
7.近日,教育部正式印发《义务教育课程方案》,将劳动从原来的综合实践活动课程中完全独立出来,并在今年9月份开学开始正式施行.某学校组织八年级同学到劳动教育基地参加实践活动,某小组的任务是平整土地300m2.开始的半小时,由于操作不熟练,只平整完30m2,学校要求完成全部任务的时间不超过3小时,若他们在剩余时间内每小时平整土地x m2,则x满足的不等关系为( )
A.30+(3﹣0.5)x≤300 B.300﹣30x﹣0.5≤3
C.30+(3﹣0.5)x≥300 D.0.5+300﹣30x≥3
8.已知一次函数y=kx+b(k≠0)的图象如图所示,则不等式kx+b≤0的解集是( )
A.x≤2 B.x<2 C.x≥2 D.x>2
9.不等式组的解集是x>2,则m的取值范围是( )
A.m≤2 B.m≥2 C.m≤1 D.m>1
10.若关于x的不等式组的整数解共有3个,则m的取值范围是( )
A.6<m<7 B.6≤m<7 C.6<m≤7 D.6≤m≤7
二.填空题(共8小题,满分32分,每小题4分)
11.“x的2倍与1的差比y小”用不等式表示为 .
12.选择适当的不等号填空:若a<b,则﹣2a ﹣2b.
13.若(m﹣2)x|m|﹣1>5是关于x的一元一次不等式,则m的值为 .
14.已知关于x的不等式的解集在数轴上表示如图所示,则这个不等式的解集是 .
15.不等式2x+11>0的负整数解有 个.
16.如图,直线y=kx+b经过点A(﹣2,﹣1)和B两点,则不等式x<kx+b的解集为 .
17.若关于x的不等式组无解,则m的取值范围是 .
18.若关于x的方程5(2﹣x)+x=ax的解为正数,且关于x的不等式组有解,则满足条件的所有整数a的值之和是 .
三.解答题(共7小题,满分58分)
19.(7分)解不等式2x﹣3<,并把它的解集在数轴上表示出来.
20.(7分)求不等式 的正整数解.
21.(7分)解不等式组并把解集在数轴上表示出来.
22.(8分)解不等式组,并写出满足条件的正整数解.
23.(8分)已知关于x,y的方程组的解x+y>0,则m的取值范围是多少?
24.(9分)“人间烟火气,最抚凡人心.”在这喧嚣的世界里,地摊的存在,让人们感受到了那份朴实无华的温暖,也让城市多了一份生活的温度.某个体户购买了腊梅,百合两种鲜花摆摊销售,若购进腊梅5束,百合3束,需要114元;若购进腊梅8束,百合6束,需要204元.
(1)求腊梅,百合两种鲜花的进价分别是每束多少元?
(2)若每束腊梅的售价为20元,每束百合的售价为30元.结合市场需求,该个体户决定购进两种鲜花共80束,计划购买成本不超过1260元,且购进百合的数量不少于腊梅数量的.两种鲜花全部销售完时,求销售的最大利润及相应的进货方案.
25.(12分)[问题提出]:如何解不等式|x﹣1|+|x﹣3|>x+2?
预备知识1:同学们学习了一元一次方程、一元一次不等式和一次函数,利用这些一次模型和函数的图象,可以解决一系列问题.
图①中给出了函数y=x+1和y=2x+3的图象,观察图象,我们可以得到:
当x>﹣2时,函数y=2x+3的图象在y=x+1图象上方,由此可知:不等式2x+3>x+1的解集为 .
预备知识2:函数y=|x|=,称为分段函数,其图象如图②所示,实际上对带有绝对值
的代数式的化简,通常采用“零点分段”的办法,将带有绝对值符号的代数式在各“取值段”化简,即可去掉绝对值符号.比如化简|x﹣1|+|x﹣3|时,可令x﹣1=0和x﹣3=0,分别求得x=1,x=3(称1,3分别是|x﹣1|和|x﹣3|的零点值),这样可以就x<1,1≤x<3,x≥3三种情况进行讨论:
(1)当x<1时,|x﹣1|+|x﹣3|=﹣(x﹣1)﹣(x﹣3)
(2)当1≤x<3时,|x﹣1|+|x﹣3|=(x﹣1)﹣(x﹣3)=2;
(3)当x≥3时,|x﹣1|+|x﹣3|=(x﹣1)+(x﹣3)=2x﹣4
所以|x﹣1+|x﹣3|就可以化简为
预备知识3:函数y=b(b为常数)称为常数函数,其图象如图③所示.
[知识迁移]
如图④,直线y=x+1与直线y=ax+b相交于点A(m,3),则关于x的不等式x+1≤ax+b的解集是 .
[问题解决]:
结合前面的预备知识,我们来研究怎样解不等式|x﹣1|+x﹣3|>x+2.在平面直角坐标系内作出函数y=|x﹣1|+|x﹣3|的图象,如图⑤.在同一直角坐标系内再作出直线y=x+2的图象,如图⑥,可以发现函数y=|x﹣1|+|x﹣3|与y=x+2的图象有两个交点,这两个交点坐标分别是 , ;
通过观察图象,便可得到不等式|x﹣1|+|x﹣3|>x+2的解集.这个不等式的解集为 .
参考答案
一.选择题(共10小题,满分30分,每小题3分)
1.解:不等式有:﹣2<0,x+2>x+1,x≠﹣2,4x+5>0,共4个,
故选:C.
2.解:若a>b,两边同时减3得a﹣3>b﹣3,则A不符合题意;
若a>b,两边同时乘﹣2得﹣2a<﹣2b,则B不符合题意;
若a>b,两边同时减b得a﹣b>0,则C符合题意;
若a>b,两边同时除以4得>,则D不符合题意;
故选:C.
3.解:A、该不等式组符合一元一次不等式组的定义,故本选项错误;
B、该不等式组中含有2给未知数,不是一元一次不等式组,故本选项正确;
C、该不等式组符合一元一次不等式组的定义,故本选项错误;
D、该不等式组符合一元一次不等式组的定义,故本选项错误;
故选:B.
4.解:不等式x>4的解集在数轴上表示,
故选:D.
5.解:由题意知,,
解得﹣3<a<2,
故选:B.
6.解:解不等式x+2>1,得:x>﹣1,
解不等式,得:x≤2,
则不等式组的解集为﹣1<x≤2,
在数轴上表示为:
故选:B.
7.解:依题意得:30+(3﹣0.5)x≥300.
故选:C.
8.解:由图象可得:当x≤2时,kx+b≤0,
所以不等式kx+b≤0的解集为x≤2,
故选:A.
9.解:∵不等式组的解集是x>2,
解不等式①得x>2,
解不等式②得x>m+1,
不等式组的解集是x>2,
∴不等式,①解集是不等式组的解集,
∴m+1≤2,
m≤1,
故选:C.
10.解:,
由①得,x≤m,
由②得,x>3,
故原不等式组的解集为:3<x≤m,
∵不等式组的整数解有3个,
∴其整数解应为:4、5、6,
∴m的取值范围是6≤m<7.
故选:B.
二.填空题(共8小题,满分32分,每小题4分)
11.解:依题意得2x﹣1<y,
故答案为:2x﹣1<y.
12.解:∵a<b,
∴﹣2a>﹣2b,
故答案为:>.
13.解:(m﹣2)x|m|﹣1>5是关于x的一元一次不等式,
由一元一次不等式的定义可得:m﹣2≠0且|m|﹣1=1.
解m﹣2≠0,得m≠2,
由|m|﹣1=1,得m=±2,
所以m=﹣2.
故答案为:m=﹣2.
14.解:这个不等式的解集是:x≥1.
故答案为:x≥1.
15.解:2x+11>0,
2x>﹣11,
x>﹣5.5,
所以不等式2x+11>0的负整数解有﹣5,﹣4,﹣3,﹣2,﹣1共5个,
故答案为:5.
16.解:不等式x<kx+b的解集为x<﹣2.
故答案为x<﹣2.
17.解:,
解不等式①得:x≤m+2,
解不等式②得:x>5,
∵关于x的不等式组无解,
∴m+2≤5,
解得:m≤3.
故答案为:m≤3.
18.解:5(2﹣x)+x=ax,
去括号:10﹣5x+x=ax,
移项:(a+4)x=10,
解得:x=,
∵关于x的方程5(2﹣x)+x=ax的解为正数,
∴a+4>0,
解得a>﹣4,
,
解不等式①得:x<1,
解不等式②得:x≥a,
∵不等式组有解,
∴a<1,
∴﹣4<a<1,
∴整数为﹣3或﹣2或﹣1或0,其和为﹣3+(﹣2)+(﹣1)+0=﹣6.
故答案为:﹣6.
三.解答题(共7小题,满分58分)
19.解:先去分母,得3(2x﹣3)<x﹣4,
去括号,得6x﹣9<x﹣4,
移项合并同类项,得5x<5,
系数化为1,得x<1
∴原不等式的解集为:x<1.
在数轴上表示为:
20.解:,
3(2x﹣5)≤7﹣2(x+3),
6x﹣15≤7﹣2x﹣6,
6x+2x≤7﹣6+15,
8x≤16,
x≤2,
∴该不等式的正整数解为:1,2.
21.解:解不等式①,得:x≥﹣2,
解不等式②,得:x<1,
则不等式组的解集为﹣2≤x<1,
将不等式组的解集表示在数轴上如下:
22.解:解不等式1﹣x<2(x+3),得:x>﹣1,
解不等式≥x+,得:x≤2,
∴不等式组的解集为﹣1<x≤2,
则不等式组的正整数解为1,2.
23.解:,
②×2﹣①,得x=2m﹣6,
把x=2m﹣6代入②得4m﹣12+y=m﹣1,
∴y=﹣3m+11,
∴x+y=5﹣m,
∵x+y>0,
∴5﹣m>0
∴m<5.
24.解:(1)设腊梅的进价是x元/束,百合的进价是y元/束,
根据题意得:,
解得:.
答:腊梅的进价是12元/束,百合的进价是18元/束;
(2)设购进腊梅m束,则购进百合(80﹣m)束,
根据题意得:,
解得:30≤m≤48,
设购进的两种鲜花全部销售完后获得的总利润为w元,则w=(20﹣12)m+(30﹣18)(80﹣m),
即w=﹣4m+960,
∵﹣4<0,
∴w随m的增大而减小,
∴当m=30时,w取得最小值,最小值=﹣4×30+960=840(元),此时80﹣m=80﹣30=50(束).
答:当购进腊梅30束,百合50束时,销售利润最大,销售的最大利润为840元.
25.解:[问题提出],如图,
∵当>﹣2时,函数y=2x+3的图象在y=x+1的图象上方,
∴不等式2x+3>x+1的解集为:x>﹣2,
故答案为:x>﹣2;
[知识迁移],如图,
∵点A(m,3)在y=x+1上,
∴m+1=3,
解得:m=2,
∴A(2,3),
∵当x≤2时,直线y=ax+b的图象在y=x+1的图象的上方,
∴不等式ax+b≥x+1,
即x+1≤ax+b的解集为:x≤2,
故答案为:x≤2;
[问题解决],如图,
设y=|x﹣1|+|x﹣3|,
根据题意得:
y=|x﹣1|+|x﹣3|=,
由函数图象得:
y=4﹣2x与y=x+2有交点,
则,
解得:,
y=2x﹣4与y=x+2有交点,
则,
解得:,
∴y=|x﹣1|+|x﹣3|与y=x+2的两个交点坐标分别为:();(6,8),
故答案为:();(6,8);
由函数图象可知,当x时,y=|x﹣1|+|x﹣3|的图象在y=x+2的上方,
当x>6时,y=|x﹣1|+|x﹣3|的图象在y=x+2的上方,
故不等式|x﹣1|+|x﹣3|>x+2的解集为:x或x>6,
故答案为:x或x>6.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
