9.4.2 用边角关系判定两个三角形相似同步练习(含解析)
文档属性
| 名称 | 9.4.2 用边角关系判定两个三角形相似同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 5.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-24 08:01:21 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第九章 图形的相似
4 探索三角形相似的条件
第2课时 用边角关系判定两个三角形相似
基 础 练
练点 用边角关系判定两个三角形相似
1.下列 的正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,则在网格图中的三角形与 相似的是( )
2.如图,在四边形ABCD 中,对角线AC,BD 交于点 O,若 则图中一定相似的三角形是( )
) )
3.如图,在边长为4 的正方形ABCD中,P是BC边上的点,且 3PC,Q是 CD的中点,求证:
纠易错 因考虑问题不全面而漏解
4.在中,点D在边AB上,且点E在边AC上,当________时,以A,D,E为顶点的三角形与 相似.
提 升 练
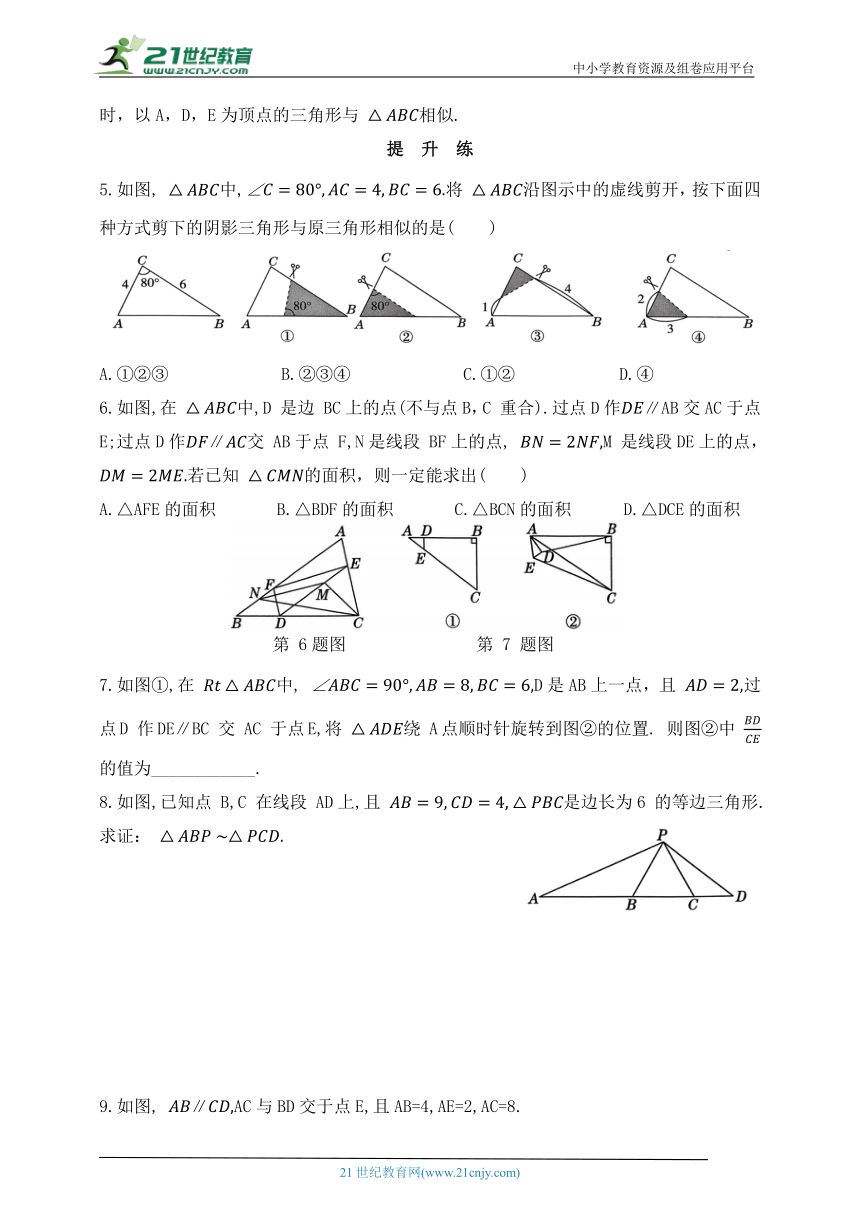
5.如图, 中,将 沿图示中的虚线剪开,按下面四种方式剪下的阴影三角形与原三角形相似的是( )
A.①②③ B.②③④ C.①② D.④
6.如图,在 中,D 是边 BC上的点(不与点B,C 重合).过点D作∥AB交AC于点E;过点D作∥交 AB于点 F,N是线段 BF上的点, M 是线段DE上的点, 若已知 的面积,则一定能求出( )
A.△AFE的面积 B.△BDF的面积 C.△BCN的面积 D.△DCE的面积
第 6题图 第 7 题图
7.如图①,在 中, D是AB上一点,且 过
点D 作DE∥BC 交 AC 于点E,将 绕 A点顺时针旋转到图②的位置. 则图②中 的值为____________.
8.如图,已知点 B,C 在线段 AD上,且 是边长为6 的等边三角形.求证:
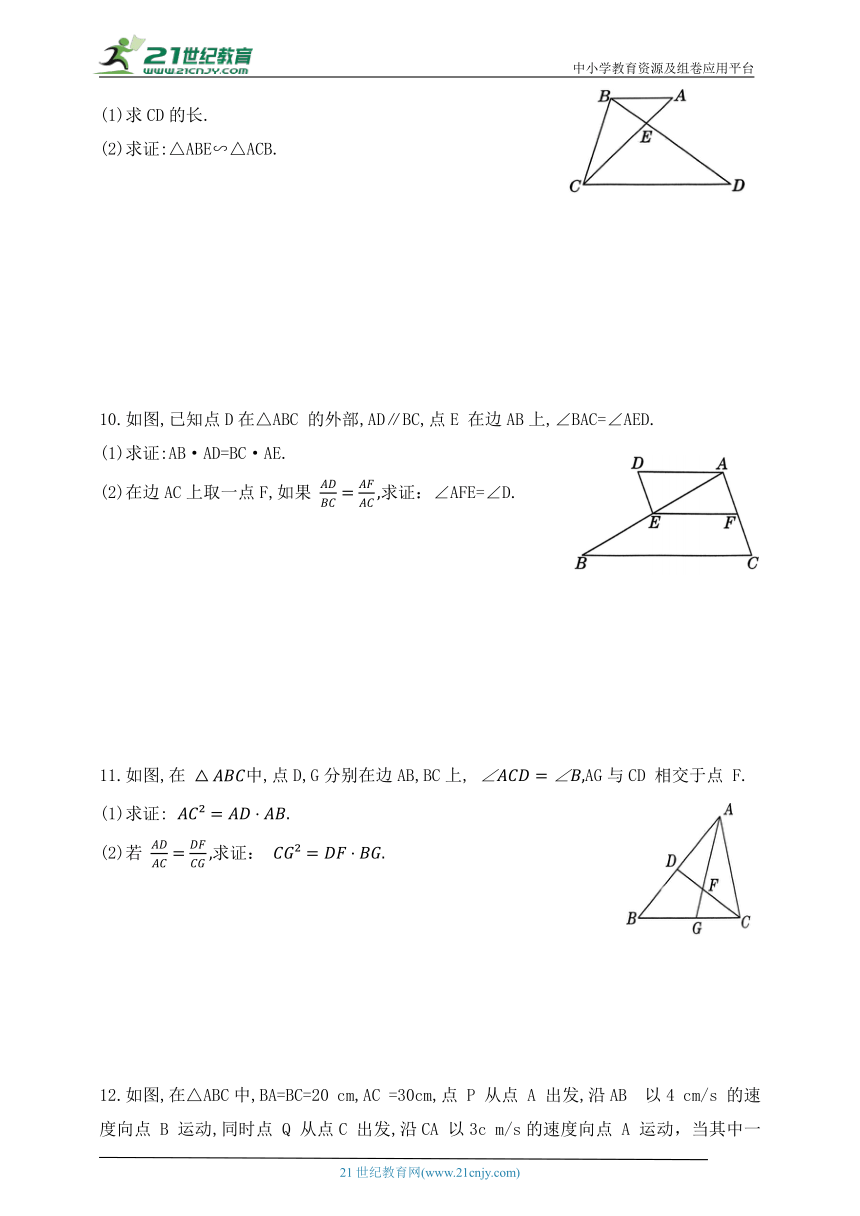
9.如图, ∥AC与BD交于点E,且AB=4,AE=2,AC=8.
(1)求CD的长.
(2)求证:△ABE∽△ACB.
10.如图,已知点D在△ABC 的外部,AD∥BC,点E 在边AB上,∠BAC=∠AED.
(1)求证:AB·AD=BC·AE.
(2)在边AC上取一点F,如果 求证:∠AFE=∠D.
11.如图,在 中,点D,G分别在边AB,BC上, AG与CD 相交于点 F.
(1)求证:
(2)若 求证:
12.如图,在△ABC中,BA=BC=20 cm,AC =30cm,点 P 从点 A 出发,沿AB 以4 cm/s 的速度向点 B 运动,同时点 Q 从点C 出发,沿CA 以3c m/s的速度向点 A 运动,当其中一点到达终点时,另一点也停止运动,设运动时间为 x s.
(1)当 ∥时,求的值.
与 能否相似 若能,求出 AP的长;若不能,请说明理由.
参考答案
1. C 【点拨】根据勾股定理, 所以 所以 是直角三角形,且 所以,夹直角的两边的比为 观察各选项,只有C 选项中的三角形与所给图形的三角形相似.
2. B 【点拨】 ∴△BOA∽△COD.
3.【证明】∵ 四边形ABCD 是正方形, Q是CD的中点,
又∵
或 【点拨】当 时, 此时
当 时, 此时
综上所述,当 或 时,以A,D,E 为顶点的三角形与 相似.
点易错 当 或 时, 以 A,D,E 为顶点的三角形与 相似,本题容易因考虑问题不全面出现漏解.
5. A 【点拨】题图①中阴影三角形与原三角形有两个角相等,故两三角形相似;题图②中阴影三角形与原三角形有两个角相等,故两三角形相似;题图③中, 两三角形对应边成比例且夹角相等,故两三角形相似;题图④中,两三角形夹相等的角的对应边不成比例,故两三角形不相似.
6. D 【点拨】连接ND. ∥∥∠DEC.∴△FBD∽△EDC,∠NFD=∠MEC.
又∵∠NFD=∠MEC,∴△NFD∽△MEC.∴∠ECM=∠FDN.
∵∠FDB =∠ECD,∴ ∠MCD =∠NDB.∥
【点拨】在题图①中,∵∠ABC =90°,AB =8,∵DE∥BC,∴∠ADE=∠ABC,∠AED=∠ACB,
将△ADE绕 A 点顺时针旋转到题图②的位置,∴ ∠DAB=∠EAC,
8.【证明】∵ △PBC是等边三角形,∴PB=PC=BC=6,∠PBC=∠PCB=60°,∴∠ABP=∠DCP=120°.
∴△ABP∽△PCD.
9.(1)【解】∵AB∥CD,∴∠A=∠DCE,∠ABE=∠D,即
∴ CD=12.
(2)【证明】∵.
又∵∠A =∠A,∴△ABE∽△ACB.
10.【证明】(1)∵AD∥BC,∴∠DAE=∠B.∵∠BAC=·AD = BC·AE.
.
∵∠EAF=∠BAC,∴△AEF∽△ABC,∴ ∠AFE=∠C.
由(1)知△ADE∽△BCA,∴∠ADE =∠C,∴∠AFE =∠D.
11.【证明】(1)∵∠ACD=∠B,∠CAD=∠BAC,
(2)过点 B 作 交AG 的延长线于点 E,则
又
又∵
.
又∵
12.【解】(1)当 时,
解得x
当 ∥时,
(2) 能. ①当 时,有 即解得
②当 时,有 即 解得 x =5 或 x = -10(舍去),
∴ AP =20cm.∴当与 相似时,AP的长为 或20 cm.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第九章 图形的相似
4 探索三角形相似的条件
第2课时 用边角关系判定两个三角形相似
基 础 练
练点 用边角关系判定两个三角形相似
1.下列 的正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,则在网格图中的三角形与 相似的是( )
2.如图,在四边形ABCD 中,对角线AC,BD 交于点 O,若 则图中一定相似的三角形是( )
) )
3.如图,在边长为4 的正方形ABCD中,P是BC边上的点,且 3PC,Q是 CD的中点,求证:
纠易错 因考虑问题不全面而漏解
4.在中,点D在边AB上,且点E在边AC上,当________时,以A,D,E为顶点的三角形与 相似.
提 升 练
5.如图, 中,将 沿图示中的虚线剪开,按下面四种方式剪下的阴影三角形与原三角形相似的是( )
A.①②③ B.②③④ C.①② D.④
6.如图,在 中,D 是边 BC上的点(不与点B,C 重合).过点D作∥AB交AC于点E;过点D作∥交 AB于点 F,N是线段 BF上的点, M 是线段DE上的点, 若已知 的面积,则一定能求出( )
A.△AFE的面积 B.△BDF的面积 C.△BCN的面积 D.△DCE的面积
第 6题图 第 7 题图
7.如图①,在 中, D是AB上一点,且 过
点D 作DE∥BC 交 AC 于点E,将 绕 A点顺时针旋转到图②的位置. 则图②中 的值为____________.
8.如图,已知点 B,C 在线段 AD上,且 是边长为6 的等边三角形.求证:
9.如图, ∥AC与BD交于点E,且AB=4,AE=2,AC=8.
(1)求CD的长.
(2)求证:△ABE∽△ACB.
10.如图,已知点D在△ABC 的外部,AD∥BC,点E 在边AB上,∠BAC=∠AED.
(1)求证:AB·AD=BC·AE.
(2)在边AC上取一点F,如果 求证:∠AFE=∠D.
11.如图,在 中,点D,G分别在边AB,BC上, AG与CD 相交于点 F.
(1)求证:
(2)若 求证:
12.如图,在△ABC中,BA=BC=20 cm,AC =30cm,点 P 从点 A 出发,沿AB 以4 cm/s 的速度向点 B 运动,同时点 Q 从点C 出发,沿CA 以3c m/s的速度向点 A 运动,当其中一点到达终点时,另一点也停止运动,设运动时间为 x s.
(1)当 ∥时,求的值.
与 能否相似 若能,求出 AP的长;若不能,请说明理由.
参考答案
1. C 【点拨】根据勾股定理, 所以 所以 是直角三角形,且 所以,夹直角的两边的比为 观察各选项,只有C 选项中的三角形与所给图形的三角形相似.
2. B 【点拨】 ∴△BOA∽△COD.
3.【证明】∵ 四边形ABCD 是正方形, Q是CD的中点,
又∵
或 【点拨】当 时, 此时
当 时, 此时
综上所述,当 或 时,以A,D,E 为顶点的三角形与 相似.
点易错 当 或 时, 以 A,D,E 为顶点的三角形与 相似,本题容易因考虑问题不全面出现漏解.
5. A 【点拨】题图①中阴影三角形与原三角形有两个角相等,故两三角形相似;题图②中阴影三角形与原三角形有两个角相等,故两三角形相似;题图③中, 两三角形对应边成比例且夹角相等,故两三角形相似;题图④中,两三角形夹相等的角的对应边不成比例,故两三角形不相似.
6. D 【点拨】连接ND. ∥∥∠DEC.∴△FBD∽△EDC,∠NFD=∠MEC.
又∵∠NFD=∠MEC,∴△NFD∽△MEC.∴∠ECM=∠FDN.
∵∠FDB =∠ECD,∴ ∠MCD =∠NDB.∥
【点拨】在题图①中,∵∠ABC =90°,AB =8,∵DE∥BC,∴∠ADE=∠ABC,∠AED=∠ACB,
将△ADE绕 A 点顺时针旋转到题图②的位置,∴ ∠DAB=∠EAC,
8.【证明】∵ △PBC是等边三角形,∴PB=PC=BC=6,∠PBC=∠PCB=60°,∴∠ABP=∠DCP=120°.
∴△ABP∽△PCD.
9.(1)【解】∵AB∥CD,∴∠A=∠DCE,∠ABE=∠D,即
∴ CD=12.
(2)【证明】∵.
又∵∠A =∠A,∴△ABE∽△ACB.
10.【证明】(1)∵AD∥BC,∴∠DAE=∠B.∵∠BAC=·AD = BC·AE.
.
∵∠EAF=∠BAC,∴△AEF∽△ABC,∴ ∠AFE=∠C.
由(1)知△ADE∽△BCA,∴∠ADE =∠C,∴∠AFE =∠D.
11.【证明】(1)∵∠ACD=∠B,∠CAD=∠BAC,
(2)过点 B 作 交AG 的延长线于点 E,则
又
又∵
.
又∵
12.【解】(1)当 时,
解得x
当 ∥时,
(2) 能. ①当 时,有 即解得
②当 时,有 即 解得 x =5 或 x = -10(舍去),
∴ AP =20cm.∴当与 相似时,AP的长为 或20 cm.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
