湘教版八下第一章 直角三角形单元测试卷(含解析)
文档属性
| 名称 | 湘教版八下第一章 直角三角形单元测试卷(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-24 07:51:15 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
湘教版八下第一章直角三角形单元测试卷
时间100分钟 满分120分
一、选择题(每小题3分,共36分)
1.下列四组线段中,可以构成直角三角形的是( )
A.2、3、4 B.、2、 C.3、4、5 D.5、6、7
2.如图,CD⊥AD于点D,CB⊥AB于点B,CD=CB,那么可以直接判定△ADC≌△ABC的定理是( )
A.AAS B.SAS C.SSS D.HL
3.直角三角形的两边长分别为3和5,则另一边长为( )
A.4 B. C.4或 D.4或
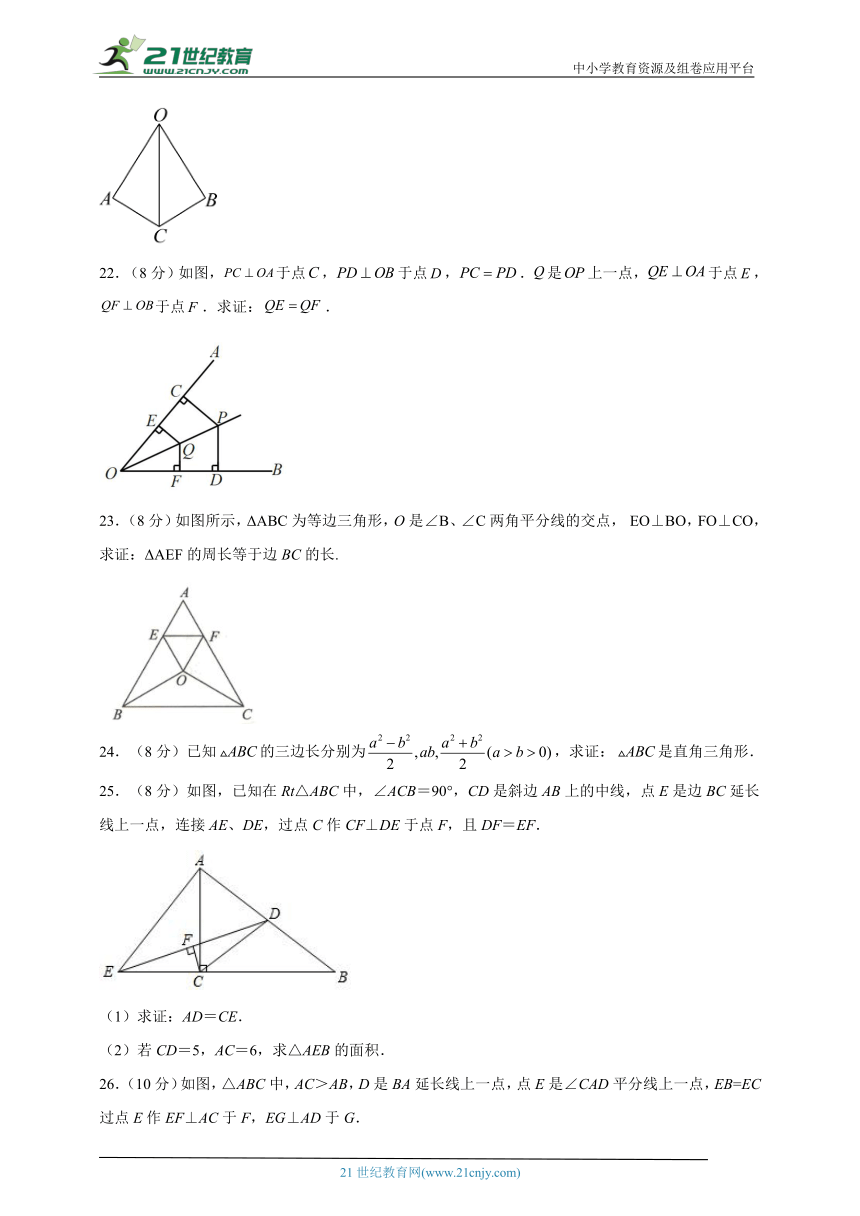
4.图是甲、乙、丙三位同学在内作的尺规作图痕迹,则其中一定能得到的是( )
A.只有甲 B.只有甲和乙 C.只有乙 D.甲、乙、丙都可以
5.以三角形的三边为边分别向外作正方形,正方形的面积分别是5,3,8,则此三角形的形状是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.任意三角形
6.下列线段不能组成直角三角形的是( ).
A.a=6,b=8,c=10 B.a=1,b=,c=
C.a=,b=1,c= D.a=2,b=3,c=
7.如图,于,于,若,,则下列结论:①;②平分;③中,正确的是( )
A.①③ B.①②③ C.①② D.②③
8.如图所示,,为平分线上一点,交于点,于点,若,则的长为( )
A.2 B.4 C.6 D.8
9.我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”,如图是由弦图变化得到,它是用八个全等的直角三角形拼接而成,记图中正方形,正方形,正方形的面积分别为,,.若,则下列关于,,的说法正确的是( )
A. B. C. D.
10.如图,在中,,,交BC于点D,,则BC的长是( )
A.8 B.9 C.10 D.11
11.如图,直线,交于点O,射线平分,若,则等于 ( )
A. B. C. D.
12.如图,在中,,,D为边上一动点,连接.以为底边,在的左侧作等腰直角三角形,点F是边上的定点,连接,当取最小值时,若,则为( )(用含的式子表示)
A. B. C. D.
二、填空题(每小题3分,共24分)
13.如图,OP平分∠AOB,PC⊥OB于点C,已知PC=5,则点P到OA的距离是 .
14.已知点,,,则点与点之间的距离为 .
15.如图,△ABC中,∠C=90°,∠BAC的平分线4D交BC于点D.BC=9,BD=6,点E在AB上,连接DE.则DE的最小值为 .
16.直角三角形纸片ABC中,∠C=90°,AC=8,AB=10,AD是∠BAC的角平分线,则BD= .
17.若,则由,,组成的三角形是 三角形.
18.如图,在平行四边形中,,,则与之间的距离为 .
19.如图,已知△ABC的周长是21,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于点D,且OD=4,△ABC的面积是 .
20.如图,AD是△ABC的角平分线,DE⊥AB,垂足为E,若△ABC的面积为15,DE=3,AB=6,则AC的长是
三、解答题(共60分)
21.(8分)如图,已知,, ,求证:.
22.(8分)如图,于点,于点,.是上一点,于点,于点.求证:.
23.(8分)如图所示,ΔABC为等边三角形,O是∠B、∠C两角平分线的交点, EO⊥BO,FO⊥CO,求证:ΔAEF的周长等于边BC的长.
24.(8分)已知的三边长分别为,求证:是直角三角形.
25.(8分)如图,已知在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,点E是边BC延长线上一点,连接AE、DE,过点C作CF⊥DE于点F,且DF=EF.
(1)求证:AD=CE.
(2)若CD=5,AC=6,求△AEB的面积.
26.(10分)如图,△ABC中,AC>AB,D是BA延长线上一点,点E是∠CAD平分线上一点,EB=EC过点E作EF⊥AC于F,EG⊥AD于G.
(1)请你在不添加辅助线的情况下找出一对你认为全等的三角形,并加以证明;
(2)若AB=3,AC=5,求AF的长.
27.(10分)在平面直角坐标系中,已知,,且,满足.
(1)求A、B两点的坐标;
(2)如图,点D为x轴正半轴上一动点,点F为线段上一动点,,,判断、、三者的数量关系,并予以证明;
(3)以为腰,为顶角顶点作等腰,若,求的长.
第一章直角三角形单元测试卷参考答案
1.C[提示:A.22+32≠42,不能作为直角三角形的三边长,故本选项不符合题意.
B. ,不能作为直角三角形的三边长,故本选项不符合题意.
C.32+42=52,能作为直角三角形的三边长,故本选项符合题意.
D.52+62≠72,不能作为直角三角形的三边长,故本选项不符合题意.
故选C.]
2.D[提示:∵CD⊥AD于点D,CB⊥AB于点B,
∴∠CDA=∠CBA=90°,
在直角△CDA与直角△CBA中,
∴(HL)
故选:D.]
3.C[提示:当长度为5的边为直角边时,则第三边;
当长度为5的边为斜边时,则第三边.
故第三边长为:或4.
故选:C.]
4.B[提示:甲图是角平分线的尺规作图的方法,可以得出;
乙图是先通过尺规取相同的弧,得到对应线段相等,再通过作平行线以及平行线的性质可以推出;
丙图画的是中线,不是角平分线,不能推出.
甲和乙可以推出.
故选:B.]
5.B[提示:解:如图,
∵,,,
而,
∴,
∴是直角三角形.
故选:B.]
6.D[提示:A、∵62+82=102,∴能组成直角三角形,故本选项错误;
B、∵12+()2=()2,∴能组成直角三角形,故本选项错误;
C、∵()2+12=()2,∴能组成直角三角形,故本选项错误;
D、∵22+()2≠32,∴不能组成直角三角形,故本选项正确.
故选:D.]
7.C[提示:∵于,于,
∴
∵,,
∴
∴,故①正确;
∴平分,故②正确;
在中,,故③错误;
故选:C.]
8.D[提示:如图,作于点,
是∠AOB平分线上一点,,,,
,,
,
,
,则
,
,
,,
,
,则
故选:D.]
9.D[提示:八个直角三角形全等,四边形,,是正方形,
,,
,
,
,
,
,
,
,
,
,
,
故选:D.]
10.B[提示:∵AB=AC,∠BAC=120°,
∴∠B=∠C=30°,
∵AD⊥AB,
∴∠DAB=90°,又∠B=30°,
∴BD=2AD=6,
∵∠BAC=120°,∠DAC=90°,
∴∠DAC=30°,
∴∠DAC=∠C,
∴CD=AD=3,
∴BC=BD+CD=9,
故选 B.]
11.D[提示;∵,
又∵平分,
∴,
∴,
故选:D.]
12.D[提示:如图,取的中点H,连接,交于,作直线,交于,
∵,,
∴,,,
∵等腰直角三角形,,
∴,
设,
取的中点,连接,,
∴,,
∴,,
∴,
∴,
∴,
∴,
∴在直线上运动,且,
∵,
∴是的垂直平分线,
∴,,
当,,三点共线时,
,此时最短,
∵,
∴,
∴,
故选D.]
13.5[提示:过P作PD⊥OA于D,如图,
即点P到OA的距离为DP的长度,
∵OP平分∠AOB,
∴OP为的角平分线,
又∵角的平分线上的点到角的两边的距离相等,PC=5,
∴DP=PC=5,
故答案为:5.]
14.[提示:AC10,
故答案为:10.]
15.3[提示:根据点到直线上的距离垂线段最短,当时,最小,
∠BAC的平分线AD交BC于点D
当时,
的最小值为3
故答案为:]
16.[提示:∵直角三角形纸片ABC中,∠C=90°,AC=8,AB=10,
∴BC=
作DE⊥AB,
∵AD是∠BAC的角平分线,
∴CD=DE,AE=AC=8
∴BE=2
设BD=x,得到DE=6-x,
在Rt△BDE中BD2=DE2+BE2
即x2=(6-x)2+22
解得x=.
故答案为:.]
17.直角[提示:根据题意得,,,,
解得,,,
,
此三角形是直角三角形 .
故答案为: 直角三角形 .]
18.[提示:作,
则,
又∵,
,
,
,
,
,
,
∴与之间的距离为,
故答案为:.]
19.42[提示:如下图,连接OA,过O作OE⊥AB于E,OF⊥AC于F,
∵OB、OC分别平分∠ABC和∠ACB,
∴OE=OF=OD=4,
∵的周长是21,OD⊥BC于D,且OD=4,
∴
=42,
故答案为:42.]
20.4[提示;过点D作DF⊥AC
∵AD是△ABC的角平分线,DF⊥AC, DE⊥AB,
∴DE=DF,
又三角形的面积的,
即,
解得AC=4]
21.证明: ,,,
在与中有:
,
22.证明:∵,,,
∴是的平分线,
∵,,
∴.
23.证明:设OE=a,因为△ABC是等边三角形,且OB,OC平分∠ABC、∠ACB,所以BE=CF=2a,
由勾股定理得:OB=a,又因为EO⊥BO,FO⊥CO,所以∠EOF=60°,
所以△EOF为等边三角形,
∴∠OEF=∠OFE=∠EOF=60°,
∴∠AEF=∠AFE=60°,
∴三角形AEF是等边三角形,
∴AE=AF=EF=a,所以EF=OE=a,BC=3a,AE+AF+EF=AB-BE+AC-CF+EF=3a-2a+3a-2a+a=3a=BC.
即△AEF的周长等于BC的长.
24.证明:
,
以为三边的是直角三角形.
25.(1)证明:∵DF=EF
∴点F为DE的中点
又∵CF⊥DE
∴CF为DE的中垂线
∴CD=CE
又∵在Rt△ABC中,∠ACB=90°,
CD是斜边AB上的中线
∴CD==AD
∴AD=CE
(2)解:由(1)得CD=CE==5
∴AB=10
∴在Rt△ABC中,BC==8
∴EB=EC+BC=13
∴ .
26.(1)△EGA≌△EFA(或△EGB≌△EFC).
证明:∵AE平分∠CAD,
∴∠EAG=∠EAF.
又∵EF⊥AC,EG⊥AD,
∴∠EGA=∠EFA=90°.
在△AEG和△EFA中:
∠EAG=∠EAF,∠EGA=∠EFA,AE=AE,
∴△EGA≌△EFA(AAS).
(2)∵AE平分∠CAD且EF⊥AC,EG⊥AD,
∴EG=EF,∠EGB=∠EFC=90°.
在Rt△EGB和Rt△EFC中
.
∴Rt△EGB≌Rt△EFC(HL).
∴BG=CF.
又∵BG=AB+AG,CF=AC-AF,
即AB+AG=AC-AF,
又∵△EGA≌△EFA,
∴AG=AF.
∴2AF=AC-AB=5-3=2.
∴AF=1.
27.(1)解:,
,
,,
,,
,,
,;
(2)解:结论:,理由如下:
如图,过点作平分交于,在上取使,连接.
设,则,
,
平分,
,
,
又,,
,
,
,,
∴,
,
;
(3)解:如图2中:当在内部,且,时,过点作于,于.设.在上取一点,连接使得.
,,
,
,
,,
,,
,
,
,
,
,
,
,
此时;
②当在的延长线上时,连接,可得,
,
都是等边三角形,
.
③当在上方时,同法可得,,
综上所述,的值为或2或.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
湘教版八下第一章直角三角形单元测试卷
时间100分钟 满分120分
一、选择题(每小题3分,共36分)
1.下列四组线段中,可以构成直角三角形的是( )
A.2、3、4 B.、2、 C.3、4、5 D.5、6、7
2.如图,CD⊥AD于点D,CB⊥AB于点B,CD=CB,那么可以直接判定△ADC≌△ABC的定理是( )
A.AAS B.SAS C.SSS D.HL
3.直角三角形的两边长分别为3和5,则另一边长为( )
A.4 B. C.4或 D.4或
4.图是甲、乙、丙三位同学在内作的尺规作图痕迹,则其中一定能得到的是( )
A.只有甲 B.只有甲和乙 C.只有乙 D.甲、乙、丙都可以
5.以三角形的三边为边分别向外作正方形,正方形的面积分别是5,3,8,则此三角形的形状是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.任意三角形
6.下列线段不能组成直角三角形的是( ).
A.a=6,b=8,c=10 B.a=1,b=,c=
C.a=,b=1,c= D.a=2,b=3,c=
7.如图,于,于,若,,则下列结论:①;②平分;③中,正确的是( )
A.①③ B.①②③ C.①② D.②③
8.如图所示,,为平分线上一点,交于点,于点,若,则的长为( )
A.2 B.4 C.6 D.8
9.我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”,如图是由弦图变化得到,它是用八个全等的直角三角形拼接而成,记图中正方形,正方形,正方形的面积分别为,,.若,则下列关于,,的说法正确的是( )
A. B. C. D.
10.如图,在中,,,交BC于点D,,则BC的长是( )
A.8 B.9 C.10 D.11
11.如图,直线,交于点O,射线平分,若,则等于 ( )
A. B. C. D.
12.如图,在中,,,D为边上一动点,连接.以为底边,在的左侧作等腰直角三角形,点F是边上的定点,连接,当取最小值时,若,则为( )(用含的式子表示)
A. B. C. D.
二、填空题(每小题3分,共24分)
13.如图,OP平分∠AOB,PC⊥OB于点C,已知PC=5,则点P到OA的距离是 .
14.已知点,,,则点与点之间的距离为 .
15.如图,△ABC中,∠C=90°,∠BAC的平分线4D交BC于点D.BC=9,BD=6,点E在AB上,连接DE.则DE的最小值为 .
16.直角三角形纸片ABC中,∠C=90°,AC=8,AB=10,AD是∠BAC的角平分线,则BD= .
17.若,则由,,组成的三角形是 三角形.
18.如图,在平行四边形中,,,则与之间的距离为 .
19.如图,已知△ABC的周长是21,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于点D,且OD=4,△ABC的面积是 .
20.如图,AD是△ABC的角平分线,DE⊥AB,垂足为E,若△ABC的面积为15,DE=3,AB=6,则AC的长是
三、解答题(共60分)
21.(8分)如图,已知,, ,求证:.
22.(8分)如图,于点,于点,.是上一点,于点,于点.求证:.
23.(8分)如图所示,ΔABC为等边三角形,O是∠B、∠C两角平分线的交点, EO⊥BO,FO⊥CO,求证:ΔAEF的周长等于边BC的长.
24.(8分)已知的三边长分别为,求证:是直角三角形.
25.(8分)如图,已知在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,点E是边BC延长线上一点,连接AE、DE,过点C作CF⊥DE于点F,且DF=EF.
(1)求证:AD=CE.
(2)若CD=5,AC=6,求△AEB的面积.
26.(10分)如图,△ABC中,AC>AB,D是BA延长线上一点,点E是∠CAD平分线上一点,EB=EC过点E作EF⊥AC于F,EG⊥AD于G.
(1)请你在不添加辅助线的情况下找出一对你认为全等的三角形,并加以证明;
(2)若AB=3,AC=5,求AF的长.
27.(10分)在平面直角坐标系中,已知,,且,满足.
(1)求A、B两点的坐标;
(2)如图,点D为x轴正半轴上一动点,点F为线段上一动点,,,判断、、三者的数量关系,并予以证明;
(3)以为腰,为顶角顶点作等腰,若,求的长.
第一章直角三角形单元测试卷参考答案
1.C[提示:A.22+32≠42,不能作为直角三角形的三边长,故本选项不符合题意.
B. ,不能作为直角三角形的三边长,故本选项不符合题意.
C.32+42=52,能作为直角三角形的三边长,故本选项符合题意.
D.52+62≠72,不能作为直角三角形的三边长,故本选项不符合题意.
故选C.]
2.D[提示:∵CD⊥AD于点D,CB⊥AB于点B,
∴∠CDA=∠CBA=90°,
在直角△CDA与直角△CBA中,
∴(HL)
故选:D.]
3.C[提示:当长度为5的边为直角边时,则第三边;
当长度为5的边为斜边时,则第三边.
故第三边长为:或4.
故选:C.]
4.B[提示:甲图是角平分线的尺规作图的方法,可以得出;
乙图是先通过尺规取相同的弧,得到对应线段相等,再通过作平行线以及平行线的性质可以推出;
丙图画的是中线,不是角平分线,不能推出.
甲和乙可以推出.
故选:B.]
5.B[提示:解:如图,
∵,,,
而,
∴,
∴是直角三角形.
故选:B.]
6.D[提示:A、∵62+82=102,∴能组成直角三角形,故本选项错误;
B、∵12+()2=()2,∴能组成直角三角形,故本选项错误;
C、∵()2+12=()2,∴能组成直角三角形,故本选项错误;
D、∵22+()2≠32,∴不能组成直角三角形,故本选项正确.
故选:D.]
7.C[提示:∵于,于,
∴
∵,,
∴
∴,故①正确;
∴平分,故②正确;
在中,,故③错误;
故选:C.]
8.D[提示:如图,作于点,
是∠AOB平分线上一点,,,,
,,
,
,
,则
,
,
,,
,
,则
故选:D.]
9.D[提示:八个直角三角形全等,四边形,,是正方形,
,,
,
,
,
,
,
,
,
,
,
,
故选:D.]
10.B[提示:∵AB=AC,∠BAC=120°,
∴∠B=∠C=30°,
∵AD⊥AB,
∴∠DAB=90°,又∠B=30°,
∴BD=2AD=6,
∵∠BAC=120°,∠DAC=90°,
∴∠DAC=30°,
∴∠DAC=∠C,
∴CD=AD=3,
∴BC=BD+CD=9,
故选 B.]
11.D[提示;∵,
又∵平分,
∴,
∴,
故选:D.]
12.D[提示:如图,取的中点H,连接,交于,作直线,交于,
∵,,
∴,,,
∵等腰直角三角形,,
∴,
设,
取的中点,连接,,
∴,,
∴,,
∴,
∴,
∴,
∴,
∴在直线上运动,且,
∵,
∴是的垂直平分线,
∴,,
当,,三点共线时,
,此时最短,
∵,
∴,
∴,
故选D.]
13.5[提示:过P作PD⊥OA于D,如图,
即点P到OA的距离为DP的长度,
∵OP平分∠AOB,
∴OP为的角平分线,
又∵角的平分线上的点到角的两边的距离相等,PC=5,
∴DP=PC=5,
故答案为:5.]
14.[提示:AC10,
故答案为:10.]
15.3[提示:根据点到直线上的距离垂线段最短,当时,最小,
∠BAC的平分线AD交BC于点D
当时,
的最小值为3
故答案为:]
16.[提示:∵直角三角形纸片ABC中,∠C=90°,AC=8,AB=10,
∴BC=
作DE⊥AB,
∵AD是∠BAC的角平分线,
∴CD=DE,AE=AC=8
∴BE=2
设BD=x,得到DE=6-x,
在Rt△BDE中BD2=DE2+BE2
即x2=(6-x)2+22
解得x=.
故答案为:.]
17.直角[提示:根据题意得,,,,
解得,,,
,
此三角形是直角三角形 .
故答案为: 直角三角形 .]
18.[提示:作,
则,
又∵,
,
,
,
,
,
,
∴与之间的距离为,
故答案为:.]
19.42[提示:如下图,连接OA,过O作OE⊥AB于E,OF⊥AC于F,
∵OB、OC分别平分∠ABC和∠ACB,
∴OE=OF=OD=4,
∵的周长是21,OD⊥BC于D,且OD=4,
∴
=42,
故答案为:42.]
20.4[提示;过点D作DF⊥AC
∵AD是△ABC的角平分线,DF⊥AC, DE⊥AB,
∴DE=DF,
又三角形的面积的,
即,
解得AC=4]
21.证明: ,,,
在与中有:
,
22.证明:∵,,,
∴是的平分线,
∵,,
∴.
23.证明:设OE=a,因为△ABC是等边三角形,且OB,OC平分∠ABC、∠ACB,所以BE=CF=2a,
由勾股定理得:OB=a,又因为EO⊥BO,FO⊥CO,所以∠EOF=60°,
所以△EOF为等边三角形,
∴∠OEF=∠OFE=∠EOF=60°,
∴∠AEF=∠AFE=60°,
∴三角形AEF是等边三角形,
∴AE=AF=EF=a,所以EF=OE=a,BC=3a,AE+AF+EF=AB-BE+AC-CF+EF=3a-2a+3a-2a+a=3a=BC.
即△AEF的周长等于BC的长.
24.证明:
,
以为三边的是直角三角形.
25.(1)证明:∵DF=EF
∴点F为DE的中点
又∵CF⊥DE
∴CF为DE的中垂线
∴CD=CE
又∵在Rt△ABC中,∠ACB=90°,
CD是斜边AB上的中线
∴CD==AD
∴AD=CE
(2)解:由(1)得CD=CE==5
∴AB=10
∴在Rt△ABC中,BC==8
∴EB=EC+BC=13
∴ .
26.(1)△EGA≌△EFA(或△EGB≌△EFC).
证明:∵AE平分∠CAD,
∴∠EAG=∠EAF.
又∵EF⊥AC,EG⊥AD,
∴∠EGA=∠EFA=90°.
在△AEG和△EFA中:
∠EAG=∠EAF,∠EGA=∠EFA,AE=AE,
∴△EGA≌△EFA(AAS).
(2)∵AE平分∠CAD且EF⊥AC,EG⊥AD,
∴EG=EF,∠EGB=∠EFC=90°.
在Rt△EGB和Rt△EFC中
.
∴Rt△EGB≌Rt△EFC(HL).
∴BG=CF.
又∵BG=AB+AG,CF=AC-AF,
即AB+AG=AC-AF,
又∵△EGA≌△EFA,
∴AG=AF.
∴2AF=AC-AB=5-3=2.
∴AF=1.
27.(1)解:,
,
,,
,,
,,
,;
(2)解:结论:,理由如下:
如图,过点作平分交于,在上取使,连接.
设,则,
,
平分,
,
,
又,,
,
,
,,
∴,
,
;
(3)解:如图2中:当在内部,且,时,过点作于,于.设.在上取一点,连接使得.
,,
,
,
,,
,,
,
,
,
,
,
,
,
此时;
②当在的延长线上时,连接,可得,
,
都是等边三角形,
.
③当在上方时,同法可得,,
综上所述,的值为或2或.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
