小学数学人教版三年级下《长方形、正方形面积的计算》表格式教案
文档属性
| 名称 | 小学数学人教版三年级下《长方形、正方形面积的计算》表格式教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 140.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-24 00:00:00 | ||
图片预览


文档简介
长方形、正方形面积的计算
教学目标:
1. 使学生经历长方形和正方形面积公式的推导过程,理解并掌握这两个面积公式,能应用公式正确计算长方形或正方形的面积,并能解决相关的简单实际问题。
2. 使学生在推导长方形、正方形面积公式的过程中,培养初步的比较、分析、抽象、概括和简单推理的能力,进一步积累学习图形与几何的经验。
3. 使学生在学习活动中,进一步体会动手实践、自主探索、合作交流的价值、增进对数学学习的积极情感。
教学重点:
让学生经历面积计算公式的推导发现过程,对平面图形面积计算推导形成认知结构,
教学难点:
在数学实验活动中,发展学生数学思维,让学生理解长方形的面积与长、宽的关系。
教学过程:
教学环节 教师活动 学生活动 设计意图
环节一 创设情境 复习激活,渗透方法 师:我们学过了哪些面积单位?怎样的正方形面积正好是1平方厘米、1平方分米、1平方米 师:下面图形的面积是多少?(每格是1平方厘米的正方形) 师:通过数一数或数数算算,你们都有什么发现呢? 师:一个图形含有面积单位的个数就是这个图形的面积。 生:我们学习的面积单位有:平方厘米、平方分米、平方米;边长是1厘米的正方形面积是1平方厘米,边长是1分米的正方形面积是1平方分米,边长是1米的正方形面积是1平方米。 生1:它们的面积分别是9平方厘米、10平方厘米、15平方厘米,我是用数格子的方法得到的,可以从左往右数或从上往下数,有几个格子面积就是几平方厘米。 生2:第三幅图也可以先数再算,因为它是长方形,先数出每排有5个,有这样的3排,再用3乘5得15,一共有15格,所以面积是15平方厘米。 生:有几个1平方厘米,它们的面积就是几平方厘米。 教师在与学生交流、复习旧知的同时唤起学生已有的知识经验,从而较好地把握了教学起点。特别是数图形的环节,学生会自然而然的用先数再算的方法推理长方形的面积,有利于学生展开对新知的探索,培养学生的空间观念。
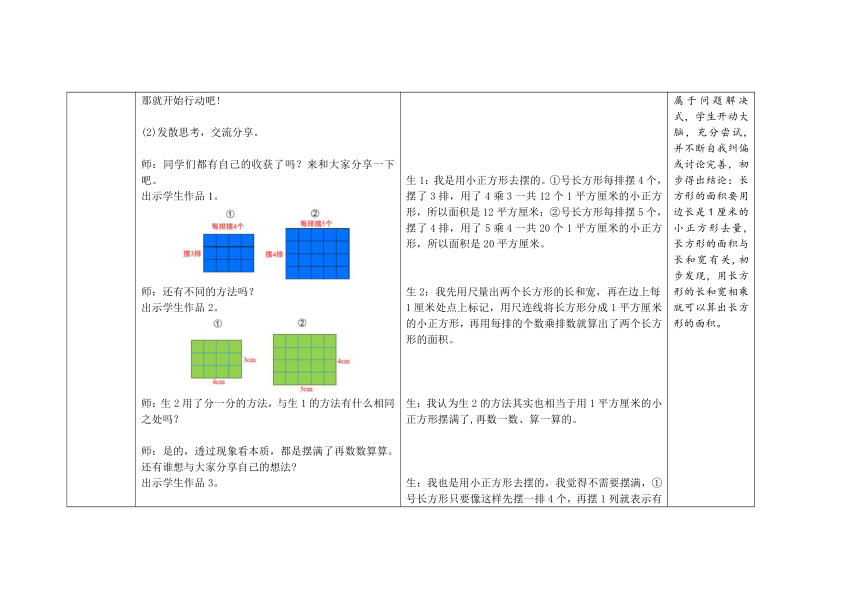
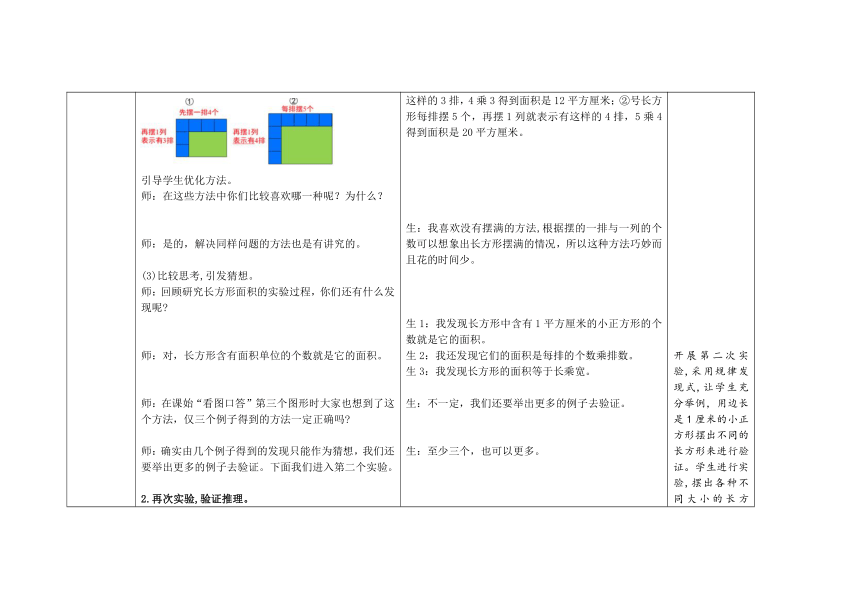
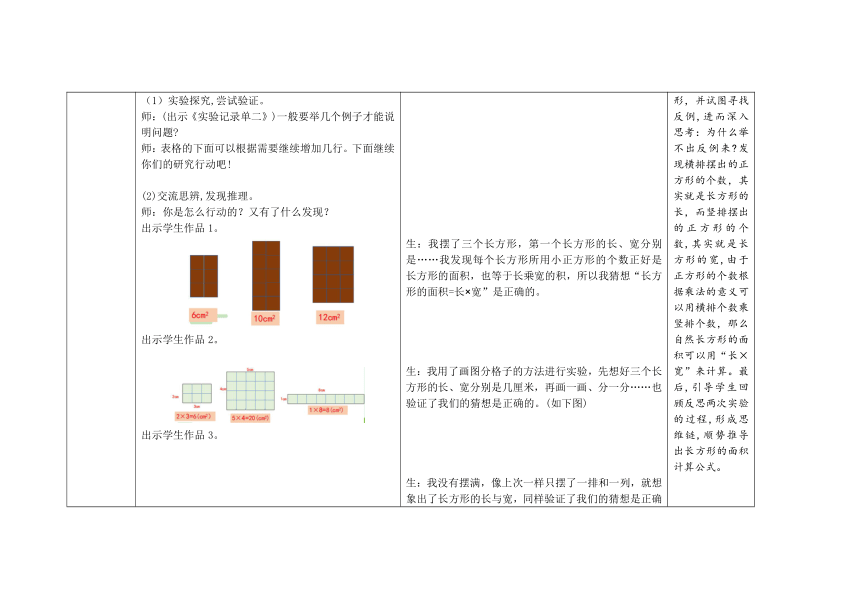
环节二 探究新知 实验探究,发现方法 1.初次实验,引发猜想。 (1)启发思考,自主探究。 师:这里有两个没有分好格子的长方形,想知道它们的面积有什么好办法呢?(揭示课题:长方形的面积) 师:(出示《实验记录单一》)同学们都有了自己的想法,那就开始行动吧! (2)发散思考,交流分享。 师:同学们都有自己的收获了吗?来和大家分享一下吧。 出示学生作品1。 师:还有不同的方法吗? 出示学生作品2。 师:生2用了分一分的方法,与生1的方法有什么相同之处吗? 师:是的,透过现象看本质,都是摆满了再数数算算。还有谁想与大家分享自己的想法 出示学生作品3。 引导学生优化方法。 师:在这些方法中你们比较喜欢哪一种呢?为什么? 师:是的,解决同样问题的方法也是有讲究的。 (3)比较思考,引发猜想。 师:回顾研究长方形面积的实验过程,你们还有什么发现呢 师:对,长方形含有面积单位的个数就是它的面积。 师:在课始“看图口答”第三个图形时大家也想到了这个方法,仅三个例子得到的方法一定正确吗 师:确实由几个例子得到的发现只能作为猜想,我们还要举出更多的例子去验证。下面我们进入第二个实验。 2.再次实验,验证推理。 (1)实验探究,尝试验证。 师:(出示《实验记录单二》)一般要举几个例子才能说明问题 师:表格的下面可以根据需要继续增加几行。下面继续你们的研究行动吧! (2)交流思辨,发现推理。 师:你是怎么行动的?又有了什么发现? 出示学生作品1。 出示学生作品2。 出示学生作品3。 师:同学们很会动脑子,大多数用了简摆的方法去举例。每个同学都至少举了三个例子,合起来已经有很多不同的例子了,例子还可以继续举下去吗 师:再举出10个、100个、1000个乃至更多的例子,就能说明我们的猜想一定是正确的吗? 师:大家可以举出无数的例子,但还不能急于下结论,有时候还要寻找有没有反例,如果一个反例也找不到就能下结论了。大家找找看,有反例吗? 师:为什么找不到反例呢?能结合刚才你们的研究过程来说说理由吗?先自己想一想,再与小组同学说一说。 师:现在我们可以认为大家的猜想是正确的吗 师:如果用S表示长方形的面积,用a和b分别表示长方形的长和宽,公式怎么简写呢? (3)延伸拓展,整体建构。 师:同学们动手动脑自己研究发现了长方形的面积计算方法,正方形的面积计算方法又是怎样的 (课题补充:正方形)你能自己思考发现吗?先自己想一想,再与同伴交流一下想法。 师:同学们根据长方形与正方形的关系推导出了正方形的面积计算公式,利用关系来推理也是很重要的本领,给自己鼓鼓掌! 师:如果用S表示正方形的面积,用a表示正方形的边长,公式又可以怎样简写 回顾反思,内化方法 师:通过刚才的学习研究,回顾一下长方形的面积公式是怎样推导出来的,正方形呢 师:是的,在许多数学方法或规律的学习中,都要经历这样的研究过程。 生1:可以用尺去量一量长方形的长、宽是多少厘米,然后分成1平方厘米的正方形格子,数数算算有几格,面积就是几。 生2:我看到学具盒里有1平方厘米的小正方形,可以用它去摆一摆,量一量,也可以知道长方形的面积。 生1:我是用小正方形去摆的。①号长方形每排摆4个,摆了3排,用了4乘3一共12个1平方厘米的小正方形,所以面积是12平方厘米;②号长方形每排摆5个,摆了4排,用了5乘4一共20个1平方厘米的小正方形,所以面积是20平方厘米。 生2:我先用尺量出两个长方形的长和宽,再在边上每1厘米处点上标记,用尺连线将长方形分成1平方厘米的小正方形,再用每排的个数乘排数就算出了两个长方形的面积。 生:我认为生2的方法其实也相当于用1平方厘米的小正方形摆满了,再数一数、算一算的。 生:我也是用小正方形去摆的,我觉得不需要摆满,①号长方形只要像这样先摆一排4个,再摆1列就表示有这样的3排,4乘3得到面积是12平方厘米;②号长方形每排摆5个,再摆1列就表示有这样的4排,5乘4得到面积是20平方厘米。 生:我喜欢没有摆满的方法,根据摆的一排与一列的个数可以想象出长方形摆满的情况,所以这种方法巧妙而且花的时间少。 生1:我发现长方形中含有1平方厘米的小正方形的个数就是它的面积。 生2:我还发现它们的面积是每排的个数乘排数。 生3:我发现长方形的面积等于长乘宽。 生:不一定,我们还要举出更多的例子去验证。 生:至少三个,也可以更多。 生:我摆了三个长方形,第一个长方形的长、宽分别是……我发现每个长方形所用小正方形的个数正好是长方形的面积,也等于长乘宽的积,所以我猜想“长方形的面积=长×宽”是正确的。 生:我用了画图分格子的方法进行实验,先想好三个长方形的长、宽分别是几厘米,再画一画、分一分……也验证了我们的猜想是正确的。(如下图) 生:我没有摆满,像上次一样只摆了一排和一列,就想象出了长方形的长与宽,同样验证了我们的猜想是正确的。 生:可以。 生:不太确定。 生:我们想到了比较特别的一种,就是摆一排的那种,每排不管是几个,1乘几面积还是几,仍然验证了我们的猜想,找不到反例。 生:不管摆多少个长方形都可以发现,长方形含有小正方形的个数就是它的面积,而小正方形的个数等于每排的个数乘排数,每排的个数就是长方形的长,排数就是长方形的宽,所以长方形的面积就等于长乘宽。 生:可以。 生: S=a×b。 (学生独立思考,小组交流) 生1:我认为正方形的面积=边长×边长,因为正方形是特殊的长方形,当长方形的长和宽相等时,长方形就变成了正方形,只要将公式中的长方形改写成正方形,长和宽改写成边长就可以了。 生2:我同意他的想法,我们可以想象,如果用边长1厘米的小正方形去摆,就摆出了每排的个数等于排数的特殊情况,所以正方形的面积=边长×边长。 生:S=a×a 生1:我们先通过几个例子的研究发现长方形的面积计算方法,由几个特殊例子得到的发现不一定正确,只能作为猜想,我们又举了更多例子去验证,并且找不到反例,最后得出结论。 生2:我们还根据正方形与长方形的关系,推出了正方形的面积计算公式。 先提出挑战性问题:“这里有两个没有分好格子的长方形,想知道它的面积有什么好办法呢 ”让学生的思维发散开来,顺势开展第一次的数学实验。该数学实验属于问题解决式,学生开动大脑,充分尝试,并不断自我纠偏或讨论完善,初步得出结论:长方形的面积要用边长是1厘米的小正方形去量,长方形的面积与长和宽有关,初步发现,用长方形的长和宽相乘就可以算出长方形的面积。 开展第二次实验,采用规律发现式,让学生充分举例,用边长是1厘米的小正方形摆出不同的长方形来进行验证。学生进行实验,摆出各种不同大小的长方形,并试图寻找反例,进而深入思考:为什么举不出反例来 发现横排摆出的正方形的个数,其实就是长方形的长,而竖排摆出的正方形的个数,其实就是长方形的宽,由于正方形的个数根据乘法的意义可以用横排个数乘竖排个数,那么自然长方形的面积可以用“长×宽”来计算。最后,引导学生回顾反思两次实验的过程,形成思维链,顺势推导出长方形的面积计算公式。 引导学生回顾反思,促使学生整理面积公式的推导方法,形成可迁移的研究方法结构,为后续的相关学习建立基础的活动经验。
环节三 练习巩固 1.看图计算。 计算下面各图形的面积。 2.想一想,画一画。 2×4 5×6 9×3 3. 挑战自我。 下图中每个小正方形表示1平方厘米,你能算出两个长方形的面积吗 生:6×4=24(平方分米) 9×9=81(平方米) 生: 生:3×4=12(平方厘米) 7×4=28(平方厘米) 第1题是基础练习题,让学生熟练掌握长方形面积计算的方法。 第2题通过画符合条件的图形,深入理解长方形面积的意义。 第3题引导学生根据已知条件找出长方形的长和宽,学生有了前期摆小正方形和分1平方厘米格子的学习经验,很快会想到解决问题的方法。
环节四 课堂小结 师:同学们通过今天的学习有什么收获 师:同学们不仅知道并会运用长方形和正方形的面积计算公式,还知道这些公式是怎么研究发现的。相信大家带着这样的研究方法与科学态度,一定会发现更多的数学奥秘。 生1:我通过两次实验推导出:长方形的面积=长×宽。 生2:由长方形的面积公式推导我还得出正方形的面积计算公式,正方形的面积=边长×边长。 生3:长方形的面积公式是“摆”出来的,以后这种方法可以用到其它公式的推导学习中去。 生4:可以利用长方形和正方形的面积公式解决一些实际问题。 引导学生整理学习的知识内容,从反思学习方法过程中习得学习经验。
环节五 拓展延伸 动手做。 把一个长12厘米、宽5厘米的长方形分成长3厘米、宽2厘米的小长方形,最多能分成多少个? 生:大长方形的面积:12×5=60(cm ) 小长方形的面积:3×2=6(cm ) 60÷6=10 最多能分成10个。 让学生在动手做的过程中更多的认识长方形的长和宽与面积的关系。
环节六 课后活动 活动:走一步大约长多少厘米?互相量一量。 (1)沿着学校篮球场的长和宽走一走,看看各走了多少步。 (2)根据步测的结果,估计篮球场的周长和面积。 要求:两人一组进行合作。为了使量出的结果更有代表性,一要用正常步伐行走,并随机测量其中一步的长度;二要多量几次,记录每次测量的结果,比较后确定自己走一步的长度。步测篮球场的长、宽时,也可要求他们多走儿次,记录每次走的步数,比较后确定长、宽各走了多少步。最后估算。 课后活动时间让学生估算学校篮球场的面积,充分使学生感受长方形的面积计算能解决生活中的实际问题,同时培养学生综合解决问题的能力。
教学目标:
1. 使学生经历长方形和正方形面积公式的推导过程,理解并掌握这两个面积公式,能应用公式正确计算长方形或正方形的面积,并能解决相关的简单实际问题。
2. 使学生在推导长方形、正方形面积公式的过程中,培养初步的比较、分析、抽象、概括和简单推理的能力,进一步积累学习图形与几何的经验。
3. 使学生在学习活动中,进一步体会动手实践、自主探索、合作交流的价值、增进对数学学习的积极情感。
教学重点:
让学生经历面积计算公式的推导发现过程,对平面图形面积计算推导形成认知结构,
教学难点:
在数学实验活动中,发展学生数学思维,让学生理解长方形的面积与长、宽的关系。
教学过程:
教学环节 教师活动 学生活动 设计意图
环节一 创设情境 复习激活,渗透方法 师:我们学过了哪些面积单位?怎样的正方形面积正好是1平方厘米、1平方分米、1平方米 师:下面图形的面积是多少?(每格是1平方厘米的正方形) 师:通过数一数或数数算算,你们都有什么发现呢? 师:一个图形含有面积单位的个数就是这个图形的面积。 生:我们学习的面积单位有:平方厘米、平方分米、平方米;边长是1厘米的正方形面积是1平方厘米,边长是1分米的正方形面积是1平方分米,边长是1米的正方形面积是1平方米。 生1:它们的面积分别是9平方厘米、10平方厘米、15平方厘米,我是用数格子的方法得到的,可以从左往右数或从上往下数,有几个格子面积就是几平方厘米。 生2:第三幅图也可以先数再算,因为它是长方形,先数出每排有5个,有这样的3排,再用3乘5得15,一共有15格,所以面积是15平方厘米。 生:有几个1平方厘米,它们的面积就是几平方厘米。 教师在与学生交流、复习旧知的同时唤起学生已有的知识经验,从而较好地把握了教学起点。特别是数图形的环节,学生会自然而然的用先数再算的方法推理长方形的面积,有利于学生展开对新知的探索,培养学生的空间观念。
环节二 探究新知 实验探究,发现方法 1.初次实验,引发猜想。 (1)启发思考,自主探究。 师:这里有两个没有分好格子的长方形,想知道它们的面积有什么好办法呢?(揭示课题:长方形的面积) 师:(出示《实验记录单一》)同学们都有了自己的想法,那就开始行动吧! (2)发散思考,交流分享。 师:同学们都有自己的收获了吗?来和大家分享一下吧。 出示学生作品1。 师:还有不同的方法吗? 出示学生作品2。 师:生2用了分一分的方法,与生1的方法有什么相同之处吗? 师:是的,透过现象看本质,都是摆满了再数数算算。还有谁想与大家分享自己的想法 出示学生作品3。 引导学生优化方法。 师:在这些方法中你们比较喜欢哪一种呢?为什么? 师:是的,解决同样问题的方法也是有讲究的。 (3)比较思考,引发猜想。 师:回顾研究长方形面积的实验过程,你们还有什么发现呢 师:对,长方形含有面积单位的个数就是它的面积。 师:在课始“看图口答”第三个图形时大家也想到了这个方法,仅三个例子得到的方法一定正确吗 师:确实由几个例子得到的发现只能作为猜想,我们还要举出更多的例子去验证。下面我们进入第二个实验。 2.再次实验,验证推理。 (1)实验探究,尝试验证。 师:(出示《实验记录单二》)一般要举几个例子才能说明问题 师:表格的下面可以根据需要继续增加几行。下面继续你们的研究行动吧! (2)交流思辨,发现推理。 师:你是怎么行动的?又有了什么发现? 出示学生作品1。 出示学生作品2。 出示学生作品3。 师:同学们很会动脑子,大多数用了简摆的方法去举例。每个同学都至少举了三个例子,合起来已经有很多不同的例子了,例子还可以继续举下去吗 师:再举出10个、100个、1000个乃至更多的例子,就能说明我们的猜想一定是正确的吗? 师:大家可以举出无数的例子,但还不能急于下结论,有时候还要寻找有没有反例,如果一个反例也找不到就能下结论了。大家找找看,有反例吗? 师:为什么找不到反例呢?能结合刚才你们的研究过程来说说理由吗?先自己想一想,再与小组同学说一说。 师:现在我们可以认为大家的猜想是正确的吗 师:如果用S表示长方形的面积,用a和b分别表示长方形的长和宽,公式怎么简写呢? (3)延伸拓展,整体建构。 师:同学们动手动脑自己研究发现了长方形的面积计算方法,正方形的面积计算方法又是怎样的 (课题补充:正方形)你能自己思考发现吗?先自己想一想,再与同伴交流一下想法。 师:同学们根据长方形与正方形的关系推导出了正方形的面积计算公式,利用关系来推理也是很重要的本领,给自己鼓鼓掌! 师:如果用S表示正方形的面积,用a表示正方形的边长,公式又可以怎样简写 回顾反思,内化方法 师:通过刚才的学习研究,回顾一下长方形的面积公式是怎样推导出来的,正方形呢 师:是的,在许多数学方法或规律的学习中,都要经历这样的研究过程。 生1:可以用尺去量一量长方形的长、宽是多少厘米,然后分成1平方厘米的正方形格子,数数算算有几格,面积就是几。 生2:我看到学具盒里有1平方厘米的小正方形,可以用它去摆一摆,量一量,也可以知道长方形的面积。 生1:我是用小正方形去摆的。①号长方形每排摆4个,摆了3排,用了4乘3一共12个1平方厘米的小正方形,所以面积是12平方厘米;②号长方形每排摆5个,摆了4排,用了5乘4一共20个1平方厘米的小正方形,所以面积是20平方厘米。 生2:我先用尺量出两个长方形的长和宽,再在边上每1厘米处点上标记,用尺连线将长方形分成1平方厘米的小正方形,再用每排的个数乘排数就算出了两个长方形的面积。 生:我认为生2的方法其实也相当于用1平方厘米的小正方形摆满了,再数一数、算一算的。 生:我也是用小正方形去摆的,我觉得不需要摆满,①号长方形只要像这样先摆一排4个,再摆1列就表示有这样的3排,4乘3得到面积是12平方厘米;②号长方形每排摆5个,再摆1列就表示有这样的4排,5乘4得到面积是20平方厘米。 生:我喜欢没有摆满的方法,根据摆的一排与一列的个数可以想象出长方形摆满的情况,所以这种方法巧妙而且花的时间少。 生1:我发现长方形中含有1平方厘米的小正方形的个数就是它的面积。 生2:我还发现它们的面积是每排的个数乘排数。 生3:我发现长方形的面积等于长乘宽。 生:不一定,我们还要举出更多的例子去验证。 生:至少三个,也可以更多。 生:我摆了三个长方形,第一个长方形的长、宽分别是……我发现每个长方形所用小正方形的个数正好是长方形的面积,也等于长乘宽的积,所以我猜想“长方形的面积=长×宽”是正确的。 生:我用了画图分格子的方法进行实验,先想好三个长方形的长、宽分别是几厘米,再画一画、分一分……也验证了我们的猜想是正确的。(如下图) 生:我没有摆满,像上次一样只摆了一排和一列,就想象出了长方形的长与宽,同样验证了我们的猜想是正确的。 生:可以。 生:不太确定。 生:我们想到了比较特别的一种,就是摆一排的那种,每排不管是几个,1乘几面积还是几,仍然验证了我们的猜想,找不到反例。 生:不管摆多少个长方形都可以发现,长方形含有小正方形的个数就是它的面积,而小正方形的个数等于每排的个数乘排数,每排的个数就是长方形的长,排数就是长方形的宽,所以长方形的面积就等于长乘宽。 生:可以。 生: S=a×b。 (学生独立思考,小组交流) 生1:我认为正方形的面积=边长×边长,因为正方形是特殊的长方形,当长方形的长和宽相等时,长方形就变成了正方形,只要将公式中的长方形改写成正方形,长和宽改写成边长就可以了。 生2:我同意他的想法,我们可以想象,如果用边长1厘米的小正方形去摆,就摆出了每排的个数等于排数的特殊情况,所以正方形的面积=边长×边长。 生:S=a×a 生1:我们先通过几个例子的研究发现长方形的面积计算方法,由几个特殊例子得到的发现不一定正确,只能作为猜想,我们又举了更多例子去验证,并且找不到反例,最后得出结论。 生2:我们还根据正方形与长方形的关系,推出了正方形的面积计算公式。 先提出挑战性问题:“这里有两个没有分好格子的长方形,想知道它的面积有什么好办法呢 ”让学生的思维发散开来,顺势开展第一次的数学实验。该数学实验属于问题解决式,学生开动大脑,充分尝试,并不断自我纠偏或讨论完善,初步得出结论:长方形的面积要用边长是1厘米的小正方形去量,长方形的面积与长和宽有关,初步发现,用长方形的长和宽相乘就可以算出长方形的面积。 开展第二次实验,采用规律发现式,让学生充分举例,用边长是1厘米的小正方形摆出不同的长方形来进行验证。学生进行实验,摆出各种不同大小的长方形,并试图寻找反例,进而深入思考:为什么举不出反例来 发现横排摆出的正方形的个数,其实就是长方形的长,而竖排摆出的正方形的个数,其实就是长方形的宽,由于正方形的个数根据乘法的意义可以用横排个数乘竖排个数,那么自然长方形的面积可以用“长×宽”来计算。最后,引导学生回顾反思两次实验的过程,形成思维链,顺势推导出长方形的面积计算公式。 引导学生回顾反思,促使学生整理面积公式的推导方法,形成可迁移的研究方法结构,为后续的相关学习建立基础的活动经验。
环节三 练习巩固 1.看图计算。 计算下面各图形的面积。 2.想一想,画一画。 2×4 5×6 9×3 3. 挑战自我。 下图中每个小正方形表示1平方厘米,你能算出两个长方形的面积吗 生:6×4=24(平方分米) 9×9=81(平方米) 生: 生:3×4=12(平方厘米) 7×4=28(平方厘米) 第1题是基础练习题,让学生熟练掌握长方形面积计算的方法。 第2题通过画符合条件的图形,深入理解长方形面积的意义。 第3题引导学生根据已知条件找出长方形的长和宽,学生有了前期摆小正方形和分1平方厘米格子的学习经验,很快会想到解决问题的方法。
环节四 课堂小结 师:同学们通过今天的学习有什么收获 师:同学们不仅知道并会运用长方形和正方形的面积计算公式,还知道这些公式是怎么研究发现的。相信大家带着这样的研究方法与科学态度,一定会发现更多的数学奥秘。 生1:我通过两次实验推导出:长方形的面积=长×宽。 生2:由长方形的面积公式推导我还得出正方形的面积计算公式,正方形的面积=边长×边长。 生3:长方形的面积公式是“摆”出来的,以后这种方法可以用到其它公式的推导学习中去。 生4:可以利用长方形和正方形的面积公式解决一些实际问题。 引导学生整理学习的知识内容,从反思学习方法过程中习得学习经验。
环节五 拓展延伸 动手做。 把一个长12厘米、宽5厘米的长方形分成长3厘米、宽2厘米的小长方形,最多能分成多少个? 生:大长方形的面积:12×5=60(cm ) 小长方形的面积:3×2=6(cm ) 60÷6=10 最多能分成10个。 让学生在动手做的过程中更多的认识长方形的长和宽与面积的关系。
环节六 课后活动 活动:走一步大约长多少厘米?互相量一量。 (1)沿着学校篮球场的长和宽走一走,看看各走了多少步。 (2)根据步测的结果,估计篮球场的周长和面积。 要求:两人一组进行合作。为了使量出的结果更有代表性,一要用正常步伐行走,并随机测量其中一步的长度;二要多量几次,记录每次测量的结果,比较后确定自己走一步的长度。步测篮球场的长、宽时,也可要求他们多走儿次,记录每次走的步数,比较后确定长、宽各走了多少步。最后估算。 课后活动时间让学生估算学校篮球场的面积,充分使学生感受长方形的面积计算能解决生活中的实际问题,同时培养学生综合解决问题的能力。
