初中数学人教版七年级下册第七章:平面直角坐标系单元复习 含解析
文档属性
| 名称 | 初中数学人教版七年级下册第七章:平面直角坐标系单元复习 含解析 |

|
|
| 格式 | docx | ||
| 文件大小 | 424.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-24 09:46:44 | ||
图片预览

文档简介
平面直角坐标系单元复习
一、单选题
1.已知点A(1,2),AC⊥x轴于C,则点C坐标为( )
A.(2,0) B.(1,0) C.(0,2) D.(0,1)
2.如图,在平面直角坐标系中,点A,C在x轴上,点C的坐标为(-1,0),AC=2,将Rt△ABC先绕点C顺时针旋转90°,再向右平移3个单位长度,则变换后点A的对应点坐标是( )
A.(2,2) B.(1,2) C.(-1,2) D.(2,-1)
3.已知点A的坐标为(0,0),点B的坐标为(4,0),点C在y轴上,△ABC的面积是10,则点C的坐标可能是( )
A.(0,10) B.(5,0) C.(0,﹣5) D.(0,4)
4.如图,直线与轴、轴分别相交于点A、,过点作,使.将绕点顺时针旋转,每次旋转.则第2024次旋转结束时,点的对应点落在反比例函数的图象上,则的值为( )
A.6 B.-6 C.-4 D.4
5.如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2)……按这样的运动规律,经过第2019次运动后,动点P的坐标是( )
A.(2018,2) B.(2019,0) C.(2019,1) D.(2019,2)
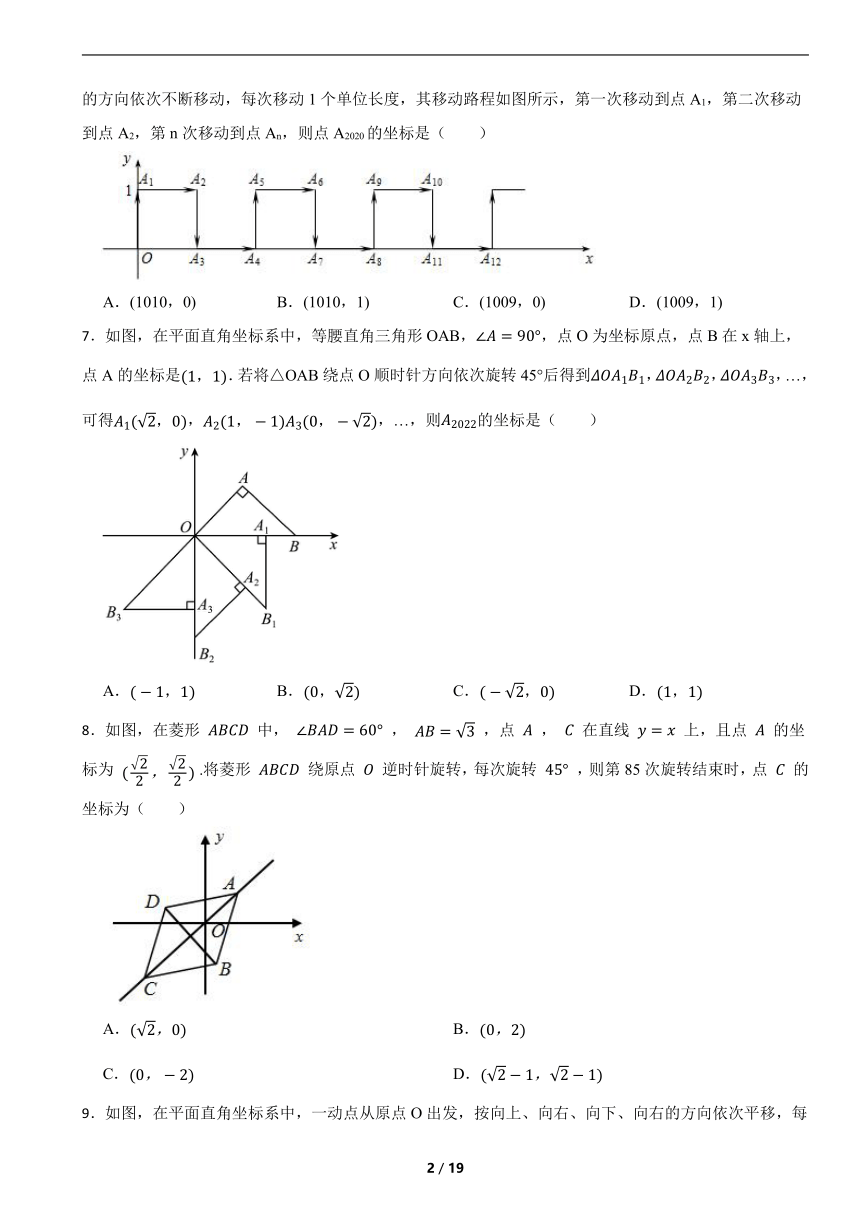
6.在平面直角坐标系中,一个智能机器人接到的指令是:从原点O出发,按“向上→向右→向下→向右”的方向依次不断移动,每次移动1个单位长度,其移动路程如图所示,第一次移动到点A1,第二次移动到点A2,第n次移动到点An,则点A2020的坐标是( )
A.(1010,0) B.(1010,1) C.(1009,0) D.(1009,1)
7.如图,在平面直角坐标系中,等腰直角三角形OAB,,点O为坐标原点,点B在x轴上,点A的坐标是.若将△OAB绕点O顺时针方向依次旋转45°后得到,,,…,可得,,…,则的坐标是( )
A. B. C. D.
8.如图,在菱形 中, , ,点 , 在直线 上,且点 的坐标为 .将菱形 绕原点 逆时针旋转,每次旋转 ,则第85次旋转结束时,点 的坐标为( )
A. B.
C. D.
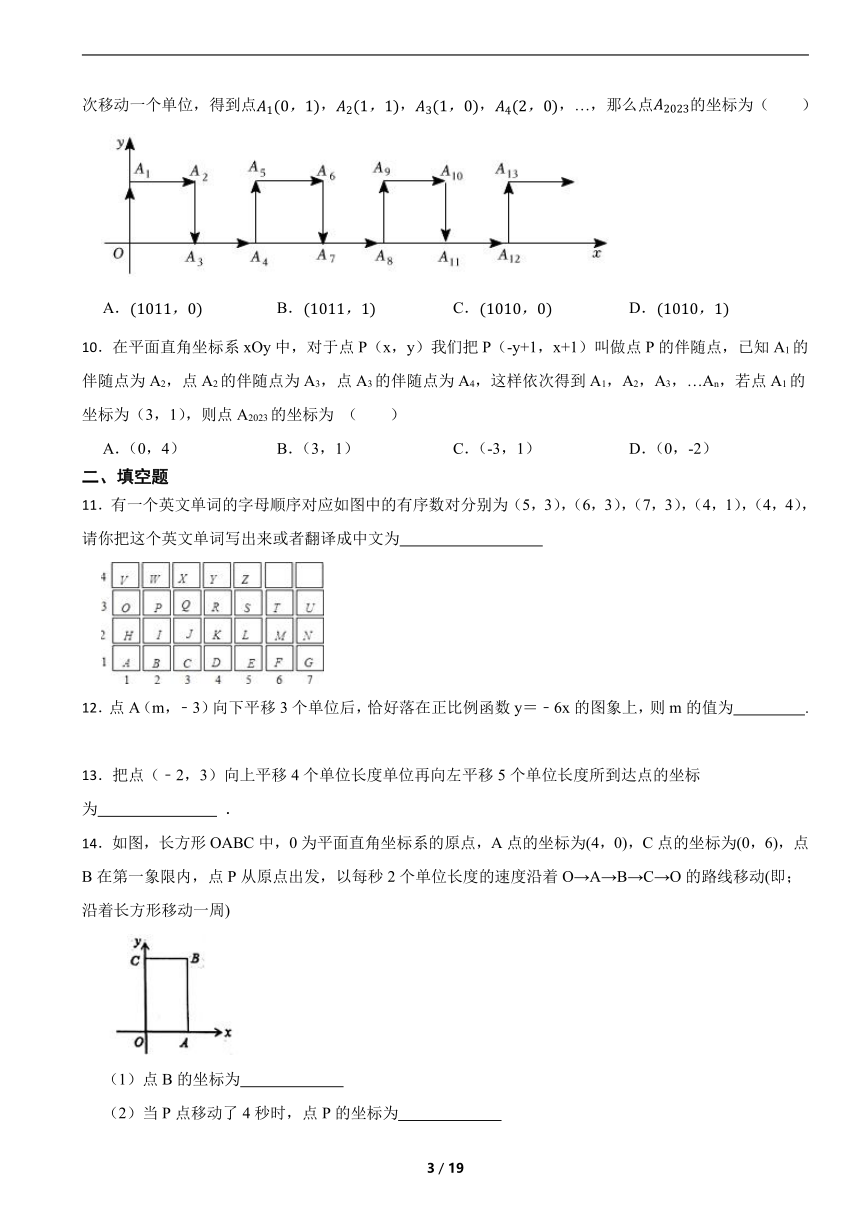
9.如图,在平面直角坐标系中,一动点从原点O出发,按向上、向右、向下、向右的方向依次平移,每次移动一个单位,得到点,,,,…,那么点的坐标为( )
A. B. C. D.
10.在平面直角坐标系xOy中,对于点P(x,y)我们把P(-y+1,x+1)叫做点P的伴随点,已知A1的伴随点为A2,点A2的伴随点为A3,点A3的伴随点为A4,这样依次得到A1,A2,A3,…An,若点A1的坐标为(3,1),则点A2023的坐标为 ( )
A.(0,4) B.(3,1) C.(-3,1) D.(0,-2)
二、填空题
11.有一个英文单词的字母顺序对应如图中的有序数对分别为(5,3),(6,3),(7,3),(4,1),(4,4),请你把这个英文单词写出来或者翻译成中文为
12.点A(m,﹣3)向下平移3个单位后,恰好落在正比例函数y=﹣6x的图象上,则m的值为 .
13.把点(﹣2,3)向上平移4个单位长度单位再向左平移5个单位长度所到达点的坐标为 .
14.如图,长方形OABC中,0为平面直角坐标系的原点,A点的坐标为(4,0),C点的坐标为(0,6),点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O→A→B→C→O的路线移动(即;沿着长方形移动一周)
(1)点B的坐标为
(2)当P点移动了4秒时,点P的坐标为
(3)在移动过程中,当点P到x轴距离为5个单位长度时,则点P移动的时间为
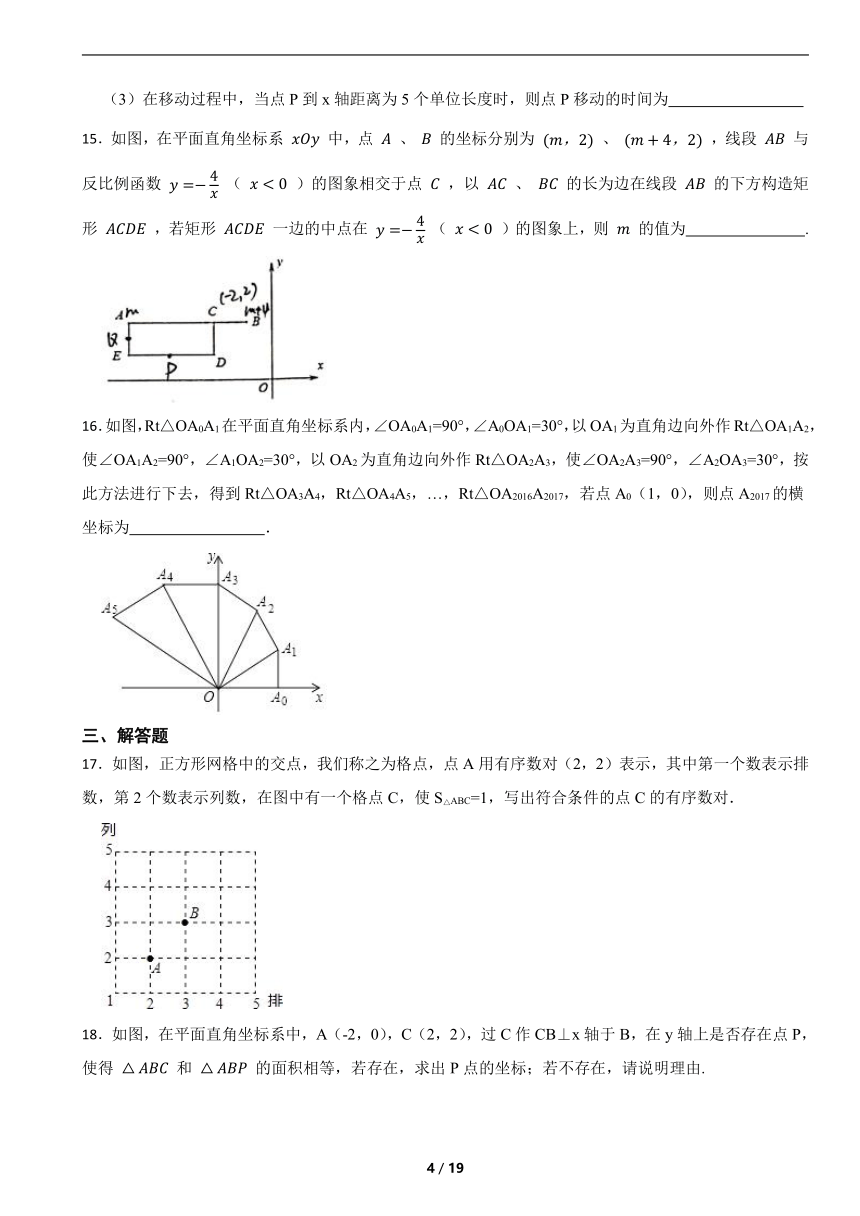
15.如图,在平面直角坐标系 中,点 、 的坐标分别为 、 ,线段 与反比例函数 ( )的图象相交于点 ,以 、 的长为边在线段 的下方构造矩形 ,若矩形 一边的中点在 ( )的图象上,则 的值为 .
16.如图,Rt△OA0A1在平面直角坐标系内,∠OA0A1=90°,∠A0OA1=30°,以OA1为直角边向外作Rt△OA1A2,使∠OA1A2=90°,∠A1OA2=30°,以OA2为直角边向外作Rt△OA2A3,使∠OA2A3=90°,∠A2OA3=30°,按此方法进行下去,得到Rt△OA3A4,Rt△OA4A5,…,Rt△OA2016A2017,若点A0(1,0),则点A2017的横坐标为 .
三、解答题
17.如图,正方形网格中的交点,我们称之为格点,点A用有序数对(2,2)表示,其中第一个数表示排数,第2个数表示列数,在图中有一个格点C,使S△ABC=1,写出符合条件的点C的有序数对.
18.如图,在平面直角坐标系中,A(-2,0),C(2,2),过C作CB⊥x轴于B,在y轴上是否存在点P,使得 和 的面积相等,若存在,求出P点的坐标;若不存在,请说明理由.
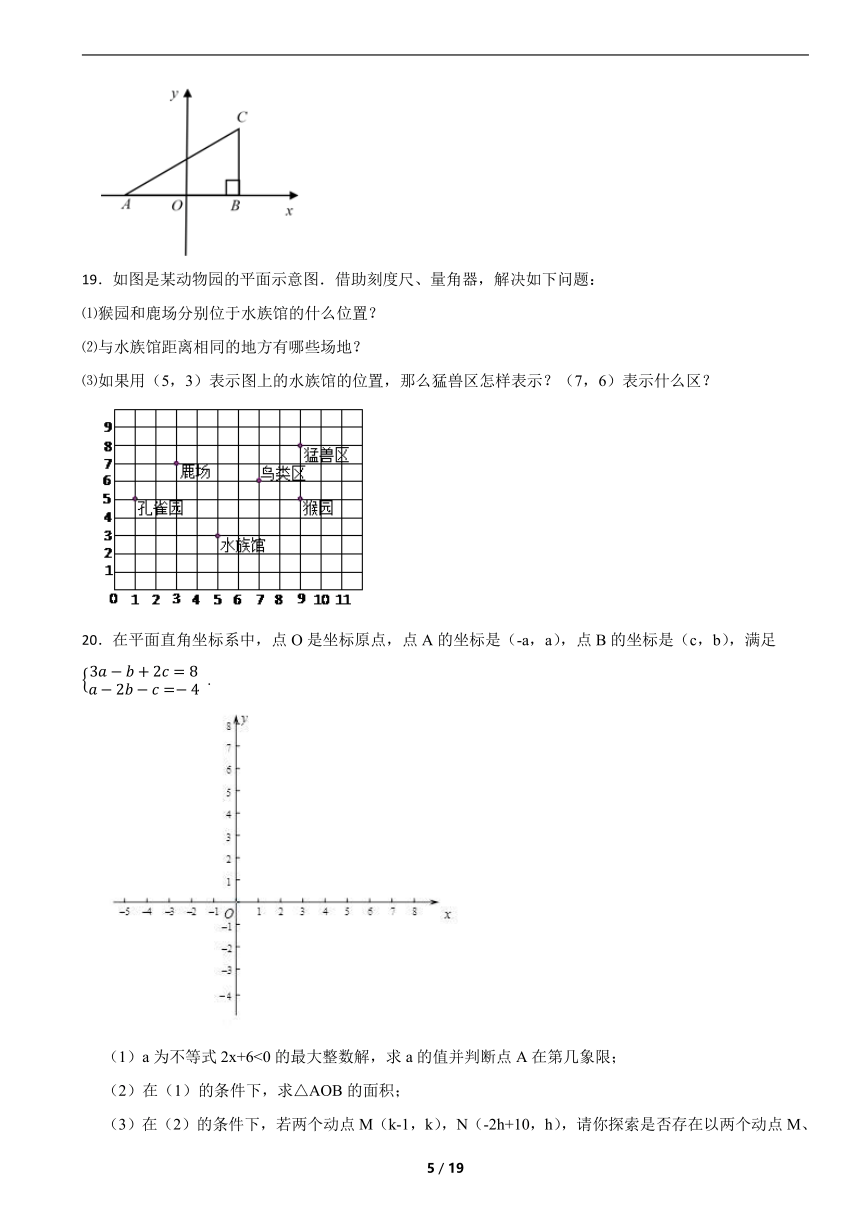
19.如图是某动物园的平面示意图.借助刻度尺、量角器,解决如下问题:
⑴猴园和鹿场分别位于水族馆的什么位置?
⑵与水族馆距离相同的地方有哪些场地?
⑶如果用(5,3)表示图上的水族馆的位置,那么猛兽区怎样表示?(7,6)表示什么区?
20.在平面直角坐标系中,点O是坐标原点,点A的坐标是(-a,a),点B的坐标是(c,b),满足 .
(1)a为不等式2x+6<0的最大整数解,求a的值并判断点A在第几象限;
(2)在(1)的条件下,求△AOB的面积;
(3)在(2)的条件下,若两个动点M(k-1,k),N(-2h+10,h),请你探索是否存在以两个动点M、N为端点的线段MN//AB,且MN=AB,若存在,求M、N两点的坐标;若不存在,请说明理由.
21.如图所示,点坐标,点在轴上,将沿轴负方向平移,平移后的图形为,且点的坐标为.
(1)请直接写出点,点的坐标 ; .
(2)在四边形中,点从点出发,沿“”移动.若点的速度为每秒1个单位长度,运动时间为秒,回答下列问题,并说明你的理由.
①求点在运动过程中的坐标(用含的式子表示)
②当为多少秒时,点的横坐标与纵坐标互为相反数.
22.如图,点的坐标为,点的坐标为,且,为轴上的一个动点,,且,连接交轴于点.
(1)求,两点坐标.
(2)若点的坐标为,求点的坐标.
(3)当点在轴上运动时,求证:为定值.
四、计算题
23.在平面直角坐标系xOy中,一次函数 的图象与y轴交于点 ,与反比例函数 的图象交于点 .
(1)求反比例函数的表达式和一次函数表达式;
(2)若点C是y轴上一点,且 ,直接写出点C的坐标.
五、实践探究题
24.在平面直角坐标系中,对于任意三点,,的“矩面积”给出如下定义:“水平底”:任意两点横坐标差的最大值,“铅垂高”:任意两点纵坐标差的最大值,则“矩面积”.、例如:三点的坐标分别为,,,则“水平底”,“铅垂高”,“矩面积”.
(1)若,,的“矩面积”为,求点的坐标.
(2)若,,,则“水平底” ,“铅垂高” ,“矩面积” ;
答案解析部分
1.【答案】B
【解析】【解答】∵ 轴于 , (1,2),
∴点 的横坐标为1,纵坐标为0,
故答案为:B.
【分析】根据平面直角坐标系得到点C的横坐标为1,纵坐标为0.
2.【答案】A
【解析】【解答】解:∵点C的坐标为(-1,0),AC=2,
∴将Rt△ABC先绕点C顺时针旋转90°后点A的对应点的坐标为(-1,2),
∴再将点(-1,2)向右平移3个单位长度后的坐标为(2,2),
故答案为:A.
【分析】利用利用旋转的性质求出点A旋转后的点坐标,再利用点坐标平移的特征:左减右加,上加下减求解即可。
3.【答案】C
【解析】【解答】解:解:设点C坐标是(0,y)根据题意得, AB×AC=10即 ×4×|y|=10,
解得y=±5.
所以点C坐标是:(0,5)或(0,﹣5).
故选C.
【分析】首先求得AB的长,根据三角形的面积公式,即可求得C的纵坐标,进而得到C的坐标.
4.【答案】B
【解析】【解答】解:如图,过点C作轴,垂足为D,如图所示:
把,代入得:,解得:,
∴,
把,代入得:,
∴,
∴,
∵,
∴,
∴,,
∴,
∴,
∴点,
第一次旋转的坐标为,第二次旋转坐标与点C关于原点对称为,第三次旋转坐标与第一次坐标关于原点对称为,第四次回到起点,
∴每4次一个循环,
∴,
∴第2024次变化后点的坐标为,
∴,故B正确.
故答案为:B.
【分析】过点C作轴,垂足为D,由求出,,可得AB=,即得BC=2,从而求出△DBC为等腰直角三角形,可得DC=BD=BC=2,从而得出C(-2,3),根据旋转可知点C每4次一个循环,由可知第2024次变化后与点C重合,即得C'坐标,继而求出K值.
5.【答案】D
【解析】【解答】解:分析图象可以发现,点P的运动每4次纵坐标循环一次,横坐标等于运动的次数,
∴2019=4×504+3,
当第504循环结束时,点P位置在(2016,0),在此基础之上运动三次到(2019,2),
故答案为:D.
【分析】分析点P的运动规律,找到循环次数即可.
6.【答案】A
【解析】【解答】A1(0,1),A2(1,1),A3(1,0),A4(2,0),A5(2,1),A6(3,1),…,
2020÷4=505,
所以A2020的坐标为(505×2,0),
则A2020的坐标是(1010,0).
故答案为:A.
【分析】根据图象可得移动4次图象完成一个循环,从而可得出点A2020的坐标.
7.【答案】A
【解析】【解答】解:∵若将△OAB绕点O顺时针方向依次旋转45°后得到,,,…
∴旋转360°÷45°=8次为一个变化周期,
2022÷8=252......6,
∴的坐标与第六次旋转后的坐标相同,
如图:
∵A的坐标是
∴
∴的坐标为
即的坐标为
故答案为:A.
【分析】易得将△OAB绕点O顺时针方向依次旋转45°后8次为一个变化周期,由于2022÷8=252......6,可知的坐标与第六次旋转后的坐标相同,画出图形求出的坐标即可.
8.【答案】B
【解析】【解答】解:由题意可得每8次旋转为一个循环,
∴85÷8=10…5,
∴第85次旋转结束时,点 的坐标与第5次旋转结束后点C坐标相同,此时点C在y轴上
∵初始位置点 的坐标为 ,且点 在直线 上
∴OA=
设菱形对角线BD与AC交于点E
由题意在菱形 中, ,
∴
∴ ,则AC=2AE=3
∴OC=AC-OA=2
即C点坐标为(0,2)
故答案为:B
【分析】根据旋转的性质,结合旋转角,先求出C点坐标,根据题意得出规律,即每8次旋转为一个循环,则第85次旋转结束时,点 的坐标与第5次旋转结束后点C坐标相同,据此解答即可.
9.【答案】A
【解析】【解答】解:由图象可知:每移动4次图象完成一个循环,每个循环结束图象向右移动2个单位,
∵2023÷4=505······3,
∴点A的坐标为(505×2+1,0),即(1011,0),
故答案为:A.
【分析】由图象可知:每移动4次图象完成一个循环,每个循环结束图象向右移动2个单位,据此解答即可.
10.【答案】C
【解析】【解答】解:的为(3,1),
.'.(0,4),(-3,1), (0,-2),(3,1)...
依此类推,每4个点为一个循环组依次循环,
∵,
∴点的坐标与的坐标相同,为(-3,1).
故答案为:C.
【分析】根据“伴随点”的定义依次求出各点,不难发现,每4个点为一个循环组依次循环,用2023除以4,根据商和余数的情况确定点的坐标即可.
11.【答案】study(学习)
【解析】【解答】解:由图形可知:(5,3)表示s;(6,3)表示t;(7,3)表示u;(4,1)表示d;(4,4)表示y.
∴这个英文单词为study,翻译成中文为学习.
故答案为:study(学习).
【分析】根据图形找出有序数对代表的每个字母,合在一起即可得出结论.
12.【答案】1
【解析】【解答】解: 点 向下平移3个单位,
平移后的点的坐标为 ,
,
故答案为:1
【分析】先求出平移后的坐标为(m,-6),然后代入y=﹣6x中,求出m的值即可.
13.【答案】(﹣7,7)
【解析】【解答】解:点(﹣2,3)向上平移4个单位长度单位再向左平移5个单位长度所到达点的坐标为(﹣2﹣5,3+4),
即(﹣7,7),
故答案为:(﹣7,7).
【分析】根据点的平移方法可得把点(﹣2,3)的横坐标减5,纵坐标加4,然后计算即可.
14.【答案】(1)(4,6)
(2)(4,4)
(3)4.5秒或7.5秒
【解析】【解答】(1)∵A(4,0)C(0,6),
∴OA=4,OC=6,
∴点B(4,6)
(2)∵点P移动4秒的距离时2×4=8,
∴点P移动到AB上且到点A的距离为4,
∴点P(4,4)
(3) 当点P到x轴距离为5个单位长度时 ,
∴点P的纵坐标为5,
当点P在AB上时,点P移动的距离为OA+AP=4+5=9,
t=9÷2=4.5秒;
当点P在OC上时,点P移动的距离为OA+AB+BC+CP=4+6+4+1=15,
t=15÷2=7.5秒;
综上所述:当点P到x轴距离为5个单位长度时 ,点P移动的时间为4.5秒或7.5秒.
【分析】(1)由A、C坐标,求出OA、OC的长,据此即得点B坐标;
(2)先求出点P移动4秒的距离,据此确定点P位置,即得坐标;
(3) 由于当点P到x轴距离为5个单位长度时 ,可得点P的纵坐标为5,分两种情况①当点P在AB上时②当点P在OC上时,据此分别求解即可.
15.【答案】-4或
【解析】【解答】解: ,
点 的纵坐标为2,
当 时, ,即 ,
,
以 、 的长为边在线段 的下方构造矩形 ,
,
,
的中点坐标为 ,即 ,
的中点坐标为 ,
由题意,分以下两种情况:
(1)当 的中点 在 的图象上时,
则 ,
解得 或 (舍去);
(2)当 的中点 在 的图象上,
则 ,
解得 或 (舍去);
综上, 的值为 或 ,
故答案为: 或 .
【分析】利用点A,B的坐标可得到点C的纵坐标,利用函数解析式求出当y=2时的x的值,可得到点C的坐标及AC,BC,DE,AE的长;由此可得到点D,E的坐标,利用线段中点坐标的计算方法求出点AE的中点坐标;再分情况讨论:当AE的中点在反比例函数图象上时,可求出符合题意的m的值;当线段DE的中点在反比例函数图象,建立关于m的方程和不等式,然后求出符合题意的m的值即可.
16.【答案】( )2016
【解析】【解答】解:∵∠OA0A1=90°,OA1= ,∠A2OA1=30°,
同理:OA2=( )2,…,OAn=( )n,
∴OA2017的长度为( )2017;
∵2017×30°÷360=168…1,
∴OA2017与OA1重合,
∴点A2017的横坐标为( )2017÷ =( )2016.
故答案为:( )2016.
【分析】根据直角三角形在坐标系中的特点,求出OA2、…、OAn 的长,探索规律得到OA2017的长度,得到点A2017的横坐标.
17.【答案】解:如图,点C可以为(1,3),(5,3),(2,4),(3,1),(3,5),(4,2).
【解析】【分析】根据A、B点间的水平距离和竖直距离都是1,找出使AC或BC为2的点C即可.
18.【答案】解:由题意,设点P的坐标为 ,则 ,
,
,
轴,
的面积为 ,
和 的面积相等,
的面积为 ,即 ,
解得 ,
故点P的坐标为 或 .
【解析】【分析】先根据点A、C的坐标可得AB、BC的长,从而可得 的面积,再根据三角形的面积公式可求出OP的长,由此即可得出答案.
19.【答案】解:⑴猴园在水族馆北偏东方向,鹿场在水族馆北偏西方向;
⑵孔雀园;鹿场和猴园;
⑶猛兽区(9,8);(7,6)表示鸟类区.
【解析】【分析】据动手测量可得出(1)(2)中的答案;(3)要利用数方格的方法确定猛兽区的位置和(7,6)表示的区.解题的关键是读懂题意,掌握平面内的点与有序实数对是一一对应关系.
20.【答案】(1)解:不等式2x+6<0的解为x<-3,x的最大整数解为-4即a=-4;
则A(4,-4),在第四象限。
(2)解:将a=-4代入题中的方程组可得 解得 则B(8,-4),如图,在坐标系在描出A(4,-4)和B(8,-4),连接OB,OA,则AB=4反向延长AB交y轴于C,可得OC=4
则 。
(3)解:由(1)、(2)可得A(4,-4),B(8,-4),
因为AB//MN,且AB=MN,所以解得k=h=5或k=h=
故M( 4 ,5),N( 0 , 5 )或M( , ),N( , )。
【解析】【分析】(1)求出不等式的解,可得a的值,和A的坐标,根据象限点坐标的特征判断;
(2)将a的值代入题中的方程组,可解得b,c的值,即求出了B的坐标,在坐标系中标出A,B, 延长AB交y轴于C ,以AB为底,OC为高,即可求出△AOB的面积;
(3)由AB=MN,且AB//MN,再根据A、B的坐标特征,即可求出M、N的坐标。
21.【答案】(1);
(2)解:①当点在上时,点的横坐标为,纵坐标为2,即,
当点在上时,点的横坐标为,纵坐标为,即;
②轴,
,
点运动到点所需时间为秒,运动到点所需时间为秒,
当点在上,即时,设,
点的横坐标与纵坐标互为相反数,
,解得,符合题意;
当点在上,即时,设,即,
点的横坐标与纵坐标互为相反数,
,解得,不符合题意,舍去;
综上,当秒时,点的横坐标与纵坐标互为相反数.
【解析】【解答】解:(1)∵点A(1,0),
∴OA=1,
∵C(-3,2),将沿轴负方向平移,平移后的图形为,
∴CD=BO=2,OD=BC=AE=3,DE=AO=1,
∴点D(-3,0),OE=3-1=2,
∴点E(-2,0)
故答案为:D(-3,0),(-2,0)
【分析】(1)利用点A的坐标可求出OA的长,再利用点C的坐标和平移的性质可得到OD,DE的长,即可求出OE的长,可得到点D和点E的坐标.
(2)①分情况讨论:当点P在BC上时,利用点的运动方向,可得到点P的坐标为(-t,2);当点P在CD上时,可得到点P的横坐标,可得到点P的坐标;②利用已知可得到BC,CD的长,同时可表示出点P运动到点C所需要的时间及运动到点D所需的时间;当点P在BC上时,0≤t≤3,可表示出点P的坐标,再根据点P的横纵坐标互为相反数,可得到关于t的方程,解方程求出t的值;当点P在CD上时,3<t≤5时,设点P(-3,5-t),同理可得到关于t的方程,解方程求出t的值;综上所述可得到符合题意的t的值.
22.【答案】(1)解:,,
又,
,,
,,
,;
(2)解:过点作轴于.
,,,
,,
,
,,
,
≌,
,,
,
.
(3)证明:≌,
,
,
,
轴,
,
,,
≌,
,
,
是定值.
【解析】【分析】(1)根据非负数之和为零,即可求出a和b的值,进而得到点A和点B的坐标;
(2)过点作轴于,结合已知信息得到:利用"AAS"证明得到:进而得到的长度,即可得到点E的坐标;
(3)由(2)中 的全等得到:结合已知条件得到:利用"AAS"证明得到:即可得到进而可证明为定值.
23.【答案】(1)∵双曲线 过 ,将 代入 ,解得: .
∴所求反比例函数表达式为: .
∵点 ,点 在直线 上,∴ , ,∴ ,∴所求一次函数表达式为 .
(2)由 , 可得: ,∴ .
又∵ ,∴ 或 ,∴ , 或 , .
【解析】【分析】(1)一次函数 过 , ,将其两点代入解析式,即可求解得到k,b的值,从而写出函数表达式。反比例函数 过 ,将其代入即可得m的值,故求出函数表达式。
(2)根据坐标利用勾股定理即可求出BA的长度,点C有两种情况,即在坐标轴原点以上或以下 。然后即可求出点C的坐标。
24.【答案】(1)解:由题意:,
当时,,
则,可得,故点的坐标为;
当时,,
则,可得,故点的坐标为;
综上,点的坐标为或
(2)6;4;24
【解析】【解答】解:(1)∵,,,
∴a=3-(-3)=6,h=2-(-2)=4,
∴S=ab=6×4=24,
故答案为:6;4;24.
【分析】(1)根据所给的定义求出a=3-(-3)=6,h=2-(-2)=4,再求解即可;
(2)根据题意先求出a=4,再分类讨论,列方程求解即可。
1 / 1
一、单选题
1.已知点A(1,2),AC⊥x轴于C,则点C坐标为( )
A.(2,0) B.(1,0) C.(0,2) D.(0,1)
2.如图,在平面直角坐标系中,点A,C在x轴上,点C的坐标为(-1,0),AC=2,将Rt△ABC先绕点C顺时针旋转90°,再向右平移3个单位长度,则变换后点A的对应点坐标是( )
A.(2,2) B.(1,2) C.(-1,2) D.(2,-1)
3.已知点A的坐标为(0,0),点B的坐标为(4,0),点C在y轴上,△ABC的面积是10,则点C的坐标可能是( )
A.(0,10) B.(5,0) C.(0,﹣5) D.(0,4)
4.如图,直线与轴、轴分别相交于点A、,过点作,使.将绕点顺时针旋转,每次旋转.则第2024次旋转结束时,点的对应点落在反比例函数的图象上,则的值为( )
A.6 B.-6 C.-4 D.4
5.如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2)……按这样的运动规律,经过第2019次运动后,动点P的坐标是( )
A.(2018,2) B.(2019,0) C.(2019,1) D.(2019,2)
6.在平面直角坐标系中,一个智能机器人接到的指令是:从原点O出发,按“向上→向右→向下→向右”的方向依次不断移动,每次移动1个单位长度,其移动路程如图所示,第一次移动到点A1,第二次移动到点A2,第n次移动到点An,则点A2020的坐标是( )
A.(1010,0) B.(1010,1) C.(1009,0) D.(1009,1)
7.如图,在平面直角坐标系中,等腰直角三角形OAB,,点O为坐标原点,点B在x轴上,点A的坐标是.若将△OAB绕点O顺时针方向依次旋转45°后得到,,,…,可得,,…,则的坐标是( )
A. B. C. D.
8.如图,在菱形 中, , ,点 , 在直线 上,且点 的坐标为 .将菱形 绕原点 逆时针旋转,每次旋转 ,则第85次旋转结束时,点 的坐标为( )
A. B.
C. D.
9.如图,在平面直角坐标系中,一动点从原点O出发,按向上、向右、向下、向右的方向依次平移,每次移动一个单位,得到点,,,,…,那么点的坐标为( )
A. B. C. D.
10.在平面直角坐标系xOy中,对于点P(x,y)我们把P(-y+1,x+1)叫做点P的伴随点,已知A1的伴随点为A2,点A2的伴随点为A3,点A3的伴随点为A4,这样依次得到A1,A2,A3,…An,若点A1的坐标为(3,1),则点A2023的坐标为 ( )
A.(0,4) B.(3,1) C.(-3,1) D.(0,-2)
二、填空题
11.有一个英文单词的字母顺序对应如图中的有序数对分别为(5,3),(6,3),(7,3),(4,1),(4,4),请你把这个英文单词写出来或者翻译成中文为
12.点A(m,﹣3)向下平移3个单位后,恰好落在正比例函数y=﹣6x的图象上,则m的值为 .
13.把点(﹣2,3)向上平移4个单位长度单位再向左平移5个单位长度所到达点的坐标为 .
14.如图,长方形OABC中,0为平面直角坐标系的原点,A点的坐标为(4,0),C点的坐标为(0,6),点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O→A→B→C→O的路线移动(即;沿着长方形移动一周)
(1)点B的坐标为
(2)当P点移动了4秒时,点P的坐标为
(3)在移动过程中,当点P到x轴距离为5个单位长度时,则点P移动的时间为
15.如图,在平面直角坐标系 中,点 、 的坐标分别为 、 ,线段 与反比例函数 ( )的图象相交于点 ,以 、 的长为边在线段 的下方构造矩形 ,若矩形 一边的中点在 ( )的图象上,则 的值为 .
16.如图,Rt△OA0A1在平面直角坐标系内,∠OA0A1=90°,∠A0OA1=30°,以OA1为直角边向外作Rt△OA1A2,使∠OA1A2=90°,∠A1OA2=30°,以OA2为直角边向外作Rt△OA2A3,使∠OA2A3=90°,∠A2OA3=30°,按此方法进行下去,得到Rt△OA3A4,Rt△OA4A5,…,Rt△OA2016A2017,若点A0(1,0),则点A2017的横坐标为 .
三、解答题
17.如图,正方形网格中的交点,我们称之为格点,点A用有序数对(2,2)表示,其中第一个数表示排数,第2个数表示列数,在图中有一个格点C,使S△ABC=1,写出符合条件的点C的有序数对.
18.如图,在平面直角坐标系中,A(-2,0),C(2,2),过C作CB⊥x轴于B,在y轴上是否存在点P,使得 和 的面积相等,若存在,求出P点的坐标;若不存在,请说明理由.
19.如图是某动物园的平面示意图.借助刻度尺、量角器,解决如下问题:
⑴猴园和鹿场分别位于水族馆的什么位置?
⑵与水族馆距离相同的地方有哪些场地?
⑶如果用(5,3)表示图上的水族馆的位置,那么猛兽区怎样表示?(7,6)表示什么区?
20.在平面直角坐标系中,点O是坐标原点,点A的坐标是(-a,a),点B的坐标是(c,b),满足 .
(1)a为不等式2x+6<0的最大整数解,求a的值并判断点A在第几象限;
(2)在(1)的条件下,求△AOB的面积;
(3)在(2)的条件下,若两个动点M(k-1,k),N(-2h+10,h),请你探索是否存在以两个动点M、N为端点的线段MN//AB,且MN=AB,若存在,求M、N两点的坐标;若不存在,请说明理由.
21.如图所示,点坐标,点在轴上,将沿轴负方向平移,平移后的图形为,且点的坐标为.
(1)请直接写出点,点的坐标 ; .
(2)在四边形中,点从点出发,沿“”移动.若点的速度为每秒1个单位长度,运动时间为秒,回答下列问题,并说明你的理由.
①求点在运动过程中的坐标(用含的式子表示)
②当为多少秒时,点的横坐标与纵坐标互为相反数.
22.如图,点的坐标为,点的坐标为,且,为轴上的一个动点,,且,连接交轴于点.
(1)求,两点坐标.
(2)若点的坐标为,求点的坐标.
(3)当点在轴上运动时,求证:为定值.
四、计算题
23.在平面直角坐标系xOy中,一次函数 的图象与y轴交于点 ,与反比例函数 的图象交于点 .
(1)求反比例函数的表达式和一次函数表达式;
(2)若点C是y轴上一点,且 ,直接写出点C的坐标.
五、实践探究题
24.在平面直角坐标系中,对于任意三点,,的“矩面积”给出如下定义:“水平底”:任意两点横坐标差的最大值,“铅垂高”:任意两点纵坐标差的最大值,则“矩面积”.、例如:三点的坐标分别为,,,则“水平底”,“铅垂高”,“矩面积”.
(1)若,,的“矩面积”为,求点的坐标.
(2)若,,,则“水平底” ,“铅垂高” ,“矩面积” ;
答案解析部分
1.【答案】B
【解析】【解答】∵ 轴于 , (1,2),
∴点 的横坐标为1,纵坐标为0,
故答案为:B.
【分析】根据平面直角坐标系得到点C的横坐标为1,纵坐标为0.
2.【答案】A
【解析】【解答】解:∵点C的坐标为(-1,0),AC=2,
∴将Rt△ABC先绕点C顺时针旋转90°后点A的对应点的坐标为(-1,2),
∴再将点(-1,2)向右平移3个单位长度后的坐标为(2,2),
故答案为:A.
【分析】利用利用旋转的性质求出点A旋转后的点坐标,再利用点坐标平移的特征:左减右加,上加下减求解即可。
3.【答案】C
【解析】【解答】解:解:设点C坐标是(0,y)根据题意得, AB×AC=10即 ×4×|y|=10,
解得y=±5.
所以点C坐标是:(0,5)或(0,﹣5).
故选C.
【分析】首先求得AB的长,根据三角形的面积公式,即可求得C的纵坐标,进而得到C的坐标.
4.【答案】B
【解析】【解答】解:如图,过点C作轴,垂足为D,如图所示:
把,代入得:,解得:,
∴,
把,代入得:,
∴,
∴,
∵,
∴,
∴,,
∴,
∴,
∴点,
第一次旋转的坐标为,第二次旋转坐标与点C关于原点对称为,第三次旋转坐标与第一次坐标关于原点对称为,第四次回到起点,
∴每4次一个循环,
∴,
∴第2024次变化后点的坐标为,
∴,故B正确.
故答案为:B.
【分析】过点C作轴,垂足为D,由求出,,可得AB=,即得BC=2,从而求出△DBC为等腰直角三角形,可得DC=BD=BC=2,从而得出C(-2,3),根据旋转可知点C每4次一个循环,由可知第2024次变化后与点C重合,即得C'坐标,继而求出K值.
5.【答案】D
【解析】【解答】解:分析图象可以发现,点P的运动每4次纵坐标循环一次,横坐标等于运动的次数,
∴2019=4×504+3,
当第504循环结束时,点P位置在(2016,0),在此基础之上运动三次到(2019,2),
故答案为:D.
【分析】分析点P的运动规律,找到循环次数即可.
6.【答案】A
【解析】【解答】A1(0,1),A2(1,1),A3(1,0),A4(2,0),A5(2,1),A6(3,1),…,
2020÷4=505,
所以A2020的坐标为(505×2,0),
则A2020的坐标是(1010,0).
故答案为:A.
【分析】根据图象可得移动4次图象完成一个循环,从而可得出点A2020的坐标.
7.【答案】A
【解析】【解答】解:∵若将△OAB绕点O顺时针方向依次旋转45°后得到,,,…
∴旋转360°÷45°=8次为一个变化周期,
2022÷8=252......6,
∴的坐标与第六次旋转后的坐标相同,
如图:
∵A的坐标是
∴
∴的坐标为
即的坐标为
故答案为:A.
【分析】易得将△OAB绕点O顺时针方向依次旋转45°后8次为一个变化周期,由于2022÷8=252......6,可知的坐标与第六次旋转后的坐标相同,画出图形求出的坐标即可.
8.【答案】B
【解析】【解答】解:由题意可得每8次旋转为一个循环,
∴85÷8=10…5,
∴第85次旋转结束时,点 的坐标与第5次旋转结束后点C坐标相同,此时点C在y轴上
∵初始位置点 的坐标为 ,且点 在直线 上
∴OA=
设菱形对角线BD与AC交于点E
由题意在菱形 中, ,
∴
∴ ,则AC=2AE=3
∴OC=AC-OA=2
即C点坐标为(0,2)
故答案为:B
【分析】根据旋转的性质,结合旋转角,先求出C点坐标,根据题意得出规律,即每8次旋转为一个循环,则第85次旋转结束时,点 的坐标与第5次旋转结束后点C坐标相同,据此解答即可.
9.【答案】A
【解析】【解答】解:由图象可知:每移动4次图象完成一个循环,每个循环结束图象向右移动2个单位,
∵2023÷4=505······3,
∴点A的坐标为(505×2+1,0),即(1011,0),
故答案为:A.
【分析】由图象可知:每移动4次图象完成一个循环,每个循环结束图象向右移动2个单位,据此解答即可.
10.【答案】C
【解析】【解答】解:的为(3,1),
.'.(0,4),(-3,1), (0,-2),(3,1)...
依此类推,每4个点为一个循环组依次循环,
∵,
∴点的坐标与的坐标相同,为(-3,1).
故答案为:C.
【分析】根据“伴随点”的定义依次求出各点,不难发现,每4个点为一个循环组依次循环,用2023除以4,根据商和余数的情况确定点的坐标即可.
11.【答案】study(学习)
【解析】【解答】解:由图形可知:(5,3)表示s;(6,3)表示t;(7,3)表示u;(4,1)表示d;(4,4)表示y.
∴这个英文单词为study,翻译成中文为学习.
故答案为:study(学习).
【分析】根据图形找出有序数对代表的每个字母,合在一起即可得出结论.
12.【答案】1
【解析】【解答】解: 点 向下平移3个单位,
平移后的点的坐标为 ,
,
故答案为:1
【分析】先求出平移后的坐标为(m,-6),然后代入y=﹣6x中,求出m的值即可.
13.【答案】(﹣7,7)
【解析】【解答】解:点(﹣2,3)向上平移4个单位长度单位再向左平移5个单位长度所到达点的坐标为(﹣2﹣5,3+4),
即(﹣7,7),
故答案为:(﹣7,7).
【分析】根据点的平移方法可得把点(﹣2,3)的横坐标减5,纵坐标加4,然后计算即可.
14.【答案】(1)(4,6)
(2)(4,4)
(3)4.5秒或7.5秒
【解析】【解答】(1)∵A(4,0)C(0,6),
∴OA=4,OC=6,
∴点B(4,6)
(2)∵点P移动4秒的距离时2×4=8,
∴点P移动到AB上且到点A的距离为4,
∴点P(4,4)
(3) 当点P到x轴距离为5个单位长度时 ,
∴点P的纵坐标为5,
当点P在AB上时,点P移动的距离为OA+AP=4+5=9,
t=9÷2=4.5秒;
当点P在OC上时,点P移动的距离为OA+AB+BC+CP=4+6+4+1=15,
t=15÷2=7.5秒;
综上所述:当点P到x轴距离为5个单位长度时 ,点P移动的时间为4.5秒或7.5秒.
【分析】(1)由A、C坐标,求出OA、OC的长,据此即得点B坐标;
(2)先求出点P移动4秒的距离,据此确定点P位置,即得坐标;
(3) 由于当点P到x轴距离为5个单位长度时 ,可得点P的纵坐标为5,分两种情况①当点P在AB上时②当点P在OC上时,据此分别求解即可.
15.【答案】-4或
【解析】【解答】解: ,
点 的纵坐标为2,
当 时, ,即 ,
,
以 、 的长为边在线段 的下方构造矩形 ,
,
,
的中点坐标为 ,即 ,
的中点坐标为 ,
由题意,分以下两种情况:
(1)当 的中点 在 的图象上时,
则 ,
解得 或 (舍去);
(2)当 的中点 在 的图象上,
则 ,
解得 或 (舍去);
综上, 的值为 或 ,
故答案为: 或 .
【分析】利用点A,B的坐标可得到点C的纵坐标,利用函数解析式求出当y=2时的x的值,可得到点C的坐标及AC,BC,DE,AE的长;由此可得到点D,E的坐标,利用线段中点坐标的计算方法求出点AE的中点坐标;再分情况讨论:当AE的中点在反比例函数图象上时,可求出符合题意的m的值;当线段DE的中点在反比例函数图象,建立关于m的方程和不等式,然后求出符合题意的m的值即可.
16.【答案】( )2016
【解析】【解答】解:∵∠OA0A1=90°,OA1= ,∠A2OA1=30°,
同理:OA2=( )2,…,OAn=( )n,
∴OA2017的长度为( )2017;
∵2017×30°÷360=168…1,
∴OA2017与OA1重合,
∴点A2017的横坐标为( )2017÷ =( )2016.
故答案为:( )2016.
【分析】根据直角三角形在坐标系中的特点,求出OA2、…、OAn 的长,探索规律得到OA2017的长度,得到点A2017的横坐标.
17.【答案】解:如图,点C可以为(1,3),(5,3),(2,4),(3,1),(3,5),(4,2).
【解析】【分析】根据A、B点间的水平距离和竖直距离都是1,找出使AC或BC为2的点C即可.
18.【答案】解:由题意,设点P的坐标为 ,则 ,
,
,
轴,
的面积为 ,
和 的面积相等,
的面积为 ,即 ,
解得 ,
故点P的坐标为 或 .
【解析】【分析】先根据点A、C的坐标可得AB、BC的长,从而可得 的面积,再根据三角形的面积公式可求出OP的长,由此即可得出答案.
19.【答案】解:⑴猴园在水族馆北偏东方向,鹿场在水族馆北偏西方向;
⑵孔雀园;鹿场和猴园;
⑶猛兽区(9,8);(7,6)表示鸟类区.
【解析】【分析】据动手测量可得出(1)(2)中的答案;(3)要利用数方格的方法确定猛兽区的位置和(7,6)表示的区.解题的关键是读懂题意,掌握平面内的点与有序实数对是一一对应关系.
20.【答案】(1)解:不等式2x+6<0的解为x<-3,x的最大整数解为-4即a=-4;
则A(4,-4),在第四象限。
(2)解:将a=-4代入题中的方程组可得 解得 则B(8,-4),如图,在坐标系在描出A(4,-4)和B(8,-4),连接OB,OA,则AB=4反向延长AB交y轴于C,可得OC=4
则 。
(3)解:由(1)、(2)可得A(4,-4),B(8,-4),
因为AB//MN,且AB=MN,所以解得k=h=5或k=h=
故M( 4 ,5),N( 0 , 5 )或M( , ),N( , )。
【解析】【分析】(1)求出不等式的解,可得a的值,和A的坐标,根据象限点坐标的特征判断;
(2)将a的值代入题中的方程组,可解得b,c的值,即求出了B的坐标,在坐标系中标出A,B, 延长AB交y轴于C ,以AB为底,OC为高,即可求出△AOB的面积;
(3)由AB=MN,且AB//MN,再根据A、B的坐标特征,即可求出M、N的坐标。
21.【答案】(1);
(2)解:①当点在上时,点的横坐标为,纵坐标为2,即,
当点在上时,点的横坐标为,纵坐标为,即;
②轴,
,
点运动到点所需时间为秒,运动到点所需时间为秒,
当点在上,即时,设,
点的横坐标与纵坐标互为相反数,
,解得,符合题意;
当点在上,即时,设,即,
点的横坐标与纵坐标互为相反数,
,解得,不符合题意,舍去;
综上,当秒时,点的横坐标与纵坐标互为相反数.
【解析】【解答】解:(1)∵点A(1,0),
∴OA=1,
∵C(-3,2),将沿轴负方向平移,平移后的图形为,
∴CD=BO=2,OD=BC=AE=3,DE=AO=1,
∴点D(-3,0),OE=3-1=2,
∴点E(-2,0)
故答案为:D(-3,0),(-2,0)
【分析】(1)利用点A的坐标可求出OA的长,再利用点C的坐标和平移的性质可得到OD,DE的长,即可求出OE的长,可得到点D和点E的坐标.
(2)①分情况讨论:当点P在BC上时,利用点的运动方向,可得到点P的坐标为(-t,2);当点P在CD上时,可得到点P的横坐标,可得到点P的坐标;②利用已知可得到BC,CD的长,同时可表示出点P运动到点C所需要的时间及运动到点D所需的时间;当点P在BC上时,0≤t≤3,可表示出点P的坐标,再根据点P的横纵坐标互为相反数,可得到关于t的方程,解方程求出t的值;当点P在CD上时,3<t≤5时,设点P(-3,5-t),同理可得到关于t的方程,解方程求出t的值;综上所述可得到符合题意的t的值.
22.【答案】(1)解:,,
又,
,,
,,
,;
(2)解:过点作轴于.
,,,
,,
,
,,
,
≌,
,,
,
.
(3)证明:≌,
,
,
,
轴,
,
,,
≌,
,
,
是定值.
【解析】【分析】(1)根据非负数之和为零,即可求出a和b的值,进而得到点A和点B的坐标;
(2)过点作轴于,结合已知信息得到:利用"AAS"证明得到:进而得到的长度,即可得到点E的坐标;
(3)由(2)中 的全等得到:结合已知条件得到:利用"AAS"证明得到:即可得到进而可证明为定值.
23.【答案】(1)∵双曲线 过 ,将 代入 ,解得: .
∴所求反比例函数表达式为: .
∵点 ,点 在直线 上,∴ , ,∴ ,∴所求一次函数表达式为 .
(2)由 , 可得: ,∴ .
又∵ ,∴ 或 ,∴ , 或 , .
【解析】【分析】(1)一次函数 过 , ,将其两点代入解析式,即可求解得到k,b的值,从而写出函数表达式。反比例函数 过 ,将其代入即可得m的值,故求出函数表达式。
(2)根据坐标利用勾股定理即可求出BA的长度,点C有两种情况,即在坐标轴原点以上或以下 。然后即可求出点C的坐标。
24.【答案】(1)解:由题意:,
当时,,
则,可得,故点的坐标为;
当时,,
则,可得,故点的坐标为;
综上,点的坐标为或
(2)6;4;24
【解析】【解答】解:(1)∵,,,
∴a=3-(-3)=6,h=2-(-2)=4,
∴S=ab=6×4=24,
故答案为:6;4;24.
【分析】(1)根据所给的定义求出a=3-(-3)=6,h=2-(-2)=4,再求解即可;
(2)根据题意先求出a=4,再分类讨论,列方程求解即可。
1 / 1
