特殊平行四边形复习
图片预览
文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
特殊平行四边形
课标要求: 1. 掌握几种特殊平行四边形的概念和性质.,以及四边形是矩形、菱形、正方形的条件,了解几种特殊四边形之间的关系。
2. 探索几种特殊平行四边形的轴对称及中心对称的特点
复习重点: 矩形、菱形、正方形的性质及判别方法的灵活运用。
考点热点: 与特殊平行四边形相关的证明计算,几何动态问题、数形结合问题、探索性问题等。
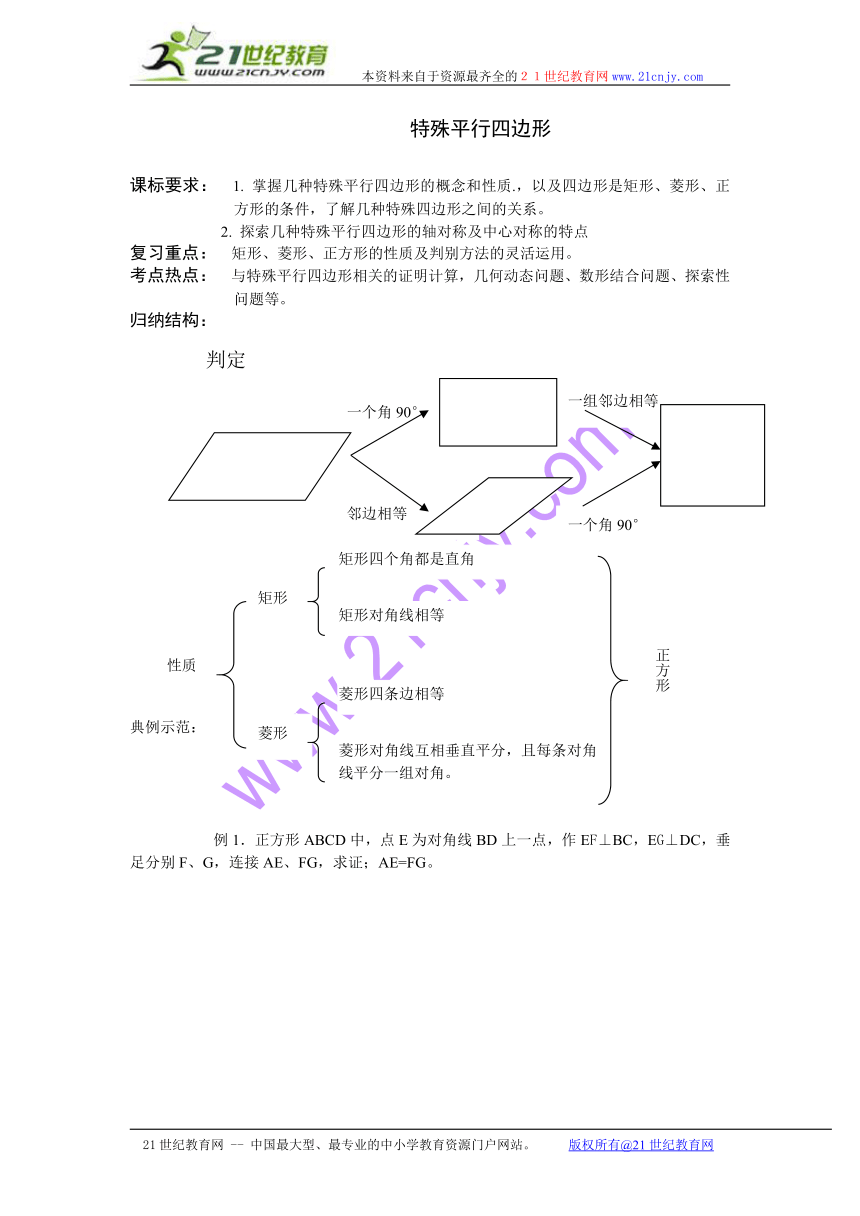
归纳结构:
典例示范:
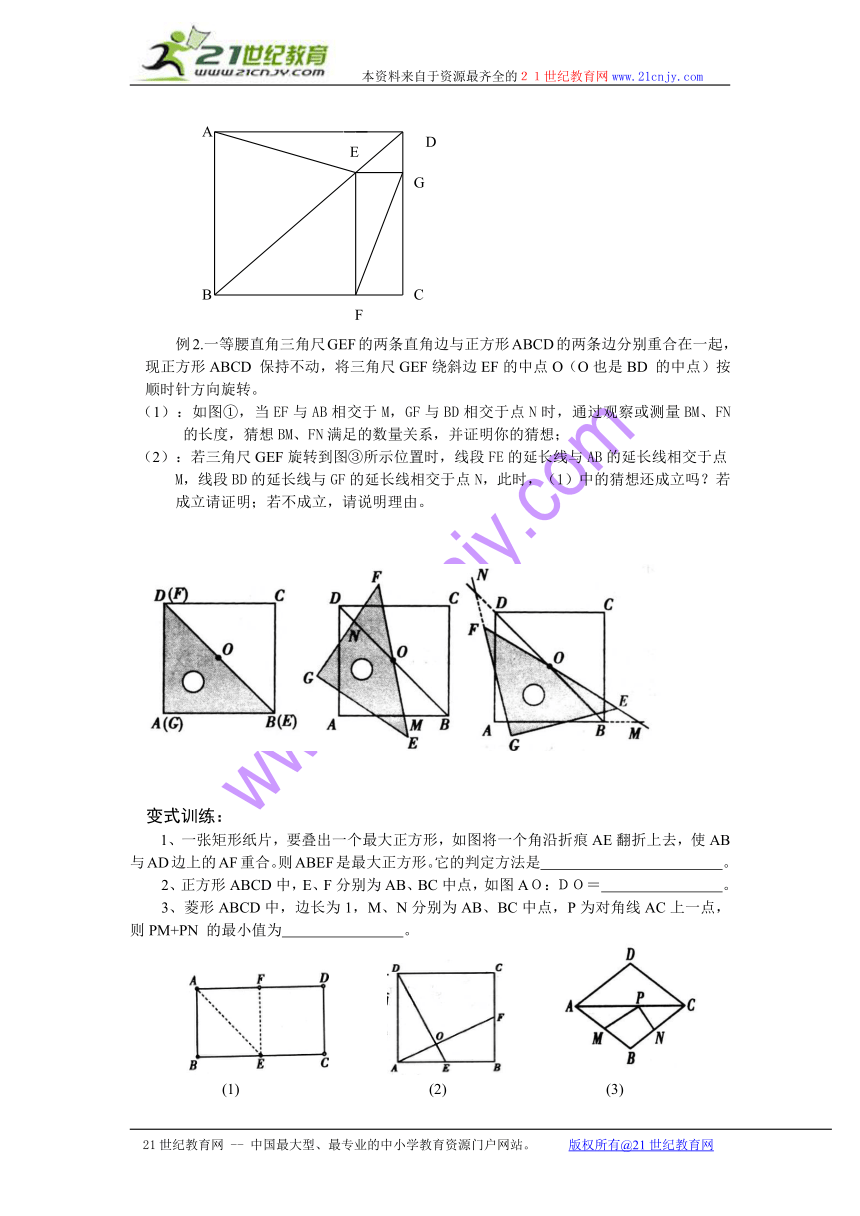
例1.正方形ABCD中,点E为对角线BD上一点,作EF⊥BC,EG⊥DC,垂足分别F、G,连接AE、FG,求证;AE=FG。
例2.一等腰直角三角尺GEF的两条直角边与正方形ABCD的两条边分别重合在一起,现正方形ABCD 保持不动,将三角尺GEF绕斜边EF的中点O(O也是BD 的中点)按顺时针方向旋转。
(1):如图①,当EF与AB相交于M,GF与BD相交于点N时,通过观察或测量BM、FN的长度,猜想BM、FN满足的数量关系,并证明你的猜想;
(2):若三角尺GEF旋转到图③所示位置时,线段FE的延长线与AB的延长线相交于点M,线段BD的延长线与GF的延长线相交于点N,此时,(1)中的猜想还成立吗?若成立请证明;若不成立,请说明理由。
变式训练:
1、一张矩形纸片,要叠出一个最大正方形,如图将一个角沿折痕AE翻折上去,使AB与AD边上的AF重合。则ABEF是最大正方形。它的判定方法是 。
2、正方形ABCD中,E、F分别为AB、BC中点,如图AO:DO= 。
3、菱形ABCD中,边长为1,M、N分别为AB、BC中点,P为对角线AC上一点,则PM+PN 的最小值为 。
(1) (2) (3)
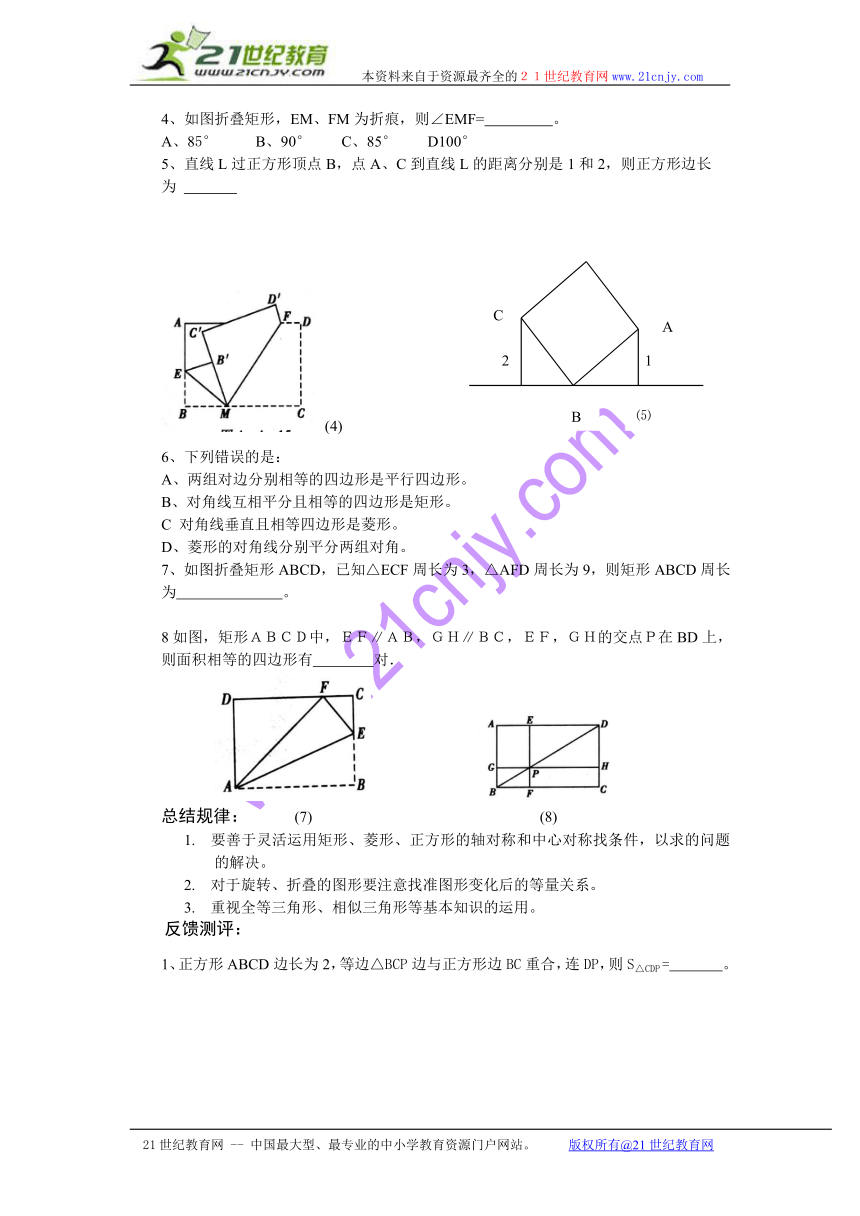
4、如图折叠矩形,EM、FM为折痕,则∠EMF= 。
A、85° B、90° C、85° D100°
5、直线L过正方形顶点B,点A、C到直线L的距离分别是1和2,则正方形边长
为
(4)
6、下列错误的是:
A、两组对边分别相等的四边形是平行四边形。
B、对角线互相平分且相等的四边形是矩形。
C 对角线垂直且相等四边形是菱形。
D、菱形的对角线分别平分两组对角。
7、如图折叠矩形ABCD,已知△ECF周长为3,△AFD周长为9,则矩形ABCD周长为 。
8如图,矩形ABCD中,EF∥AB,GH∥BC,EF,GH的交点P在BD上,则面积相等的四边形有 对.
总结规律: (7) (8)
1. 要善于灵活运用矩形、菱形、正方形的轴对称和中心对称找条件,以求的问题的解决。
2. 对于旋转、折叠的图形要注意找准图形变化后的等量关系。
3. 重视全等三角形、相似三角形等基本知识的运用。
反馈测评:
1、正方形ABCD边长为2,等边△BCP边与正方形边BC重合,连DP,则S△CDP = 。
(1) (3)
2、正方形ABCD对角线交与点O,设有下列条件:
①AB=AD②∠DAB=900 ③BO=DO AO=CO
④矩形ABCD ⑤菱形ABCD ⑥正方形ABCD。则下列推理中不成立的是:
A ①④ ⑥ B ①③ ⑤ C①② ⑥ D②③ ④
3直角三角形中,∠A=90°,AB=4,AC=3,D在BC上运动(不与B、C重合),过D点分别向AB、AC作垂线,垂足分别为E、F,则矩形AEDF的面积的最大值是 。
4如图, 正方形ABCD内有一边长与正方形边长相等的正三角形ABP,如果让正方形方框在射线AE上翻滚,正三角形也在正方形内翻滚,规定沿顺时针方向每旋转90°为一次翻滚,那么翻滚 次后,可以回到初始状态?
5如图,正方形边长为2, 每个正方形都经过另一个正方形的中心
则S阴= 。
6正方形ABCD边长为12,将顶点A折
叠至DC边上的点E,使DE=5折痕为
PQ,则PQ= 。
7如图,AD平分∠BAC,DE∥AC,DF∥AB,求证:四边形AEDF是菱形
证明:∵ AD平分∠BAC∴
∴ ∠1=∠2
∵ DE∥AC
∴ ∠2=∠3
∴ ∠1=∠3
∴ AE=DE
同理可证 AF=DF
∴ 四边形AEDF是菱形
老师说小林证明有错误
(1) 请你指出他的错误,并说明理由。
(2) 请你帮小林做出正确解答。
(7) (8)
8已知∠AOB,OA=OB,点E在OB边上,四边形AEBF是矩形,请你只用无刻度的直尺在图中作出∠AOB的平分线。(保留作图痕迹)
9矩形ABCD中,AD=4,AB=10,按如图方式折叠,使点B与点D重合,折痕为EF,则DE=
10、菱形ABCD的对角线的长分别为2和5,P是对角线BD上任一点(点P不与点B、D重合),且PE∥BC交CD于E,PF∥CD交AD于F,连接EF交PD于G,则阴影部分的面积
(9) (10)
11、如图,正方形ABCD中,E是CD边中点,AC与BE交于点F,连接DF。
(1)在不增加点和线的前提下,直接写出图中所有的全等三角形;
(2)连接AE, 试判断AE与DF的位置关系,并证明你的结论;
(3)延长DF交BC于点M,试判断BM与MC得数量关系。(直接写出结论)
12、梯形ABCD中,AD∥BC,AD﹥CD,将纸片沿过点D的直线折叠,使点C落在AD上的点C′处,折痕DE交BC与点E,连接C′E。
(1)求证:四边形CDC′E是菱形;
(2)若BC=CD+AD,试判断四边形ABED的形状,并加以证明。
(11) (12)
思考题:如图①,在正方形ABCD中,点E、F分别为BC、CD的中点,AF、DE相交于点G,则有结论①AF=DE;②AF⊥DE。(不必证明)(1)如图②若点E、F不是正方形ABCD边BC、CD的中点,但满足CE=DF。则上面结论①②仍然成立吗?(请直接回答“成立|或不成立)(2)如图③若点E、F分别在正方形ABCD的边CB的延长线和边DC的延长线上,且满足CE=DF,此时上面结论①②仍然成立吗?若成立,请写出证明过程,若不成立,请说明理由;(3)如图④,在(2)的基础上,连接AE、EF,若点M、N、P、Q分别为AE、EF、FD、DA的中点,请判断四边形MNPQ是“矩形、菱形、正方形、等腰梯形中的哪一种?并写出证明过程。
特殊平行四边形答案
变式训练:
1. 邻边相等的矩形是正方形 2. 3. 1
4. B 5. 6. C 7. 12
8. 5
反馈测评:
1. 1 2. C 3. 3 4. 12
5. 4 6. 13 7. 略 8. 略
9 . 5.8 10. 11. (1) 略 (2) AE⊥DF (3) BM=CM 12. 略
思考题:⑴ 成立 ⑵ 成立 ,证明略 ⑶ 正方形,证明略
思考条
一个角90°
一组邻边相等
邻边相等
一个角90°
判定
性质
矩形四个角都是直角
矩形
菱形
矩形对角线相等
菱形四条边相等
菱形对角线互相垂直平分,且每条对角线平分一组对角。
正方形
G
F
D
C
B
A
E
1
2
B
A
C
⑸
⑸题题
C
D
A
B
P
⑷
E
⑹
C
E
B
A
D
C′
A
B
C
D
A
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
特殊平行四边形
课标要求: 1. 掌握几种特殊平行四边形的概念和性质.,以及四边形是矩形、菱形、正方形的条件,了解几种特殊四边形之间的关系。
2. 探索几种特殊平行四边形的轴对称及中心对称的特点
复习重点: 矩形、菱形、正方形的性质及判别方法的灵活运用。
考点热点: 与特殊平行四边形相关的证明计算,几何动态问题、数形结合问题、探索性问题等。
归纳结构:
典例示范:
例1.正方形ABCD中,点E为对角线BD上一点,作EF⊥BC,EG⊥DC,垂足分别F、G,连接AE、FG,求证;AE=FG。
例2.一等腰直角三角尺GEF的两条直角边与正方形ABCD的两条边分别重合在一起,现正方形ABCD 保持不动,将三角尺GEF绕斜边EF的中点O(O也是BD 的中点)按顺时针方向旋转。
(1):如图①,当EF与AB相交于M,GF与BD相交于点N时,通过观察或测量BM、FN的长度,猜想BM、FN满足的数量关系,并证明你的猜想;
(2):若三角尺GEF旋转到图③所示位置时,线段FE的延长线与AB的延长线相交于点M,线段BD的延长线与GF的延长线相交于点N,此时,(1)中的猜想还成立吗?若成立请证明;若不成立,请说明理由。
变式训练:
1、一张矩形纸片,要叠出一个最大正方形,如图将一个角沿折痕AE翻折上去,使AB与AD边上的AF重合。则ABEF是最大正方形。它的判定方法是 。
2、正方形ABCD中,E、F分别为AB、BC中点,如图AO:DO= 。
3、菱形ABCD中,边长为1,M、N分别为AB、BC中点,P为对角线AC上一点,则PM+PN 的最小值为 。
(1) (2) (3)
4、如图折叠矩形,EM、FM为折痕,则∠EMF= 。
A、85° B、90° C、85° D100°
5、直线L过正方形顶点B,点A、C到直线L的距离分别是1和2,则正方形边长
为
(4)
6、下列错误的是:
A、两组对边分别相等的四边形是平行四边形。
B、对角线互相平分且相等的四边形是矩形。
C 对角线垂直且相等四边形是菱形。
D、菱形的对角线分别平分两组对角。
7、如图折叠矩形ABCD,已知△ECF周长为3,△AFD周长为9,则矩形ABCD周长为 。
8如图,矩形ABCD中,EF∥AB,GH∥BC,EF,GH的交点P在BD上,则面积相等的四边形有 对.
总结规律: (7) (8)
1. 要善于灵活运用矩形、菱形、正方形的轴对称和中心对称找条件,以求的问题的解决。
2. 对于旋转、折叠的图形要注意找准图形变化后的等量关系。
3. 重视全等三角形、相似三角形等基本知识的运用。
反馈测评:
1、正方形ABCD边长为2,等边△BCP边与正方形边BC重合,连DP,则S△CDP = 。
(1) (3)
2、正方形ABCD对角线交与点O,设有下列条件:
①AB=AD②∠DAB=900 ③BO=DO AO=CO
④矩形ABCD ⑤菱形ABCD ⑥正方形ABCD。则下列推理中不成立的是:
A ①④ ⑥ B ①③ ⑤ C①② ⑥ D②③ ④
3直角三角形中,∠A=90°,AB=4,AC=3,D在BC上运动(不与B、C重合),过D点分别向AB、AC作垂线,垂足分别为E、F,则矩形AEDF的面积的最大值是 。
4如图, 正方形ABCD内有一边长与正方形边长相等的正三角形ABP,如果让正方形方框在射线AE上翻滚,正三角形也在正方形内翻滚,规定沿顺时针方向每旋转90°为一次翻滚,那么翻滚 次后,可以回到初始状态?
5如图,正方形边长为2, 每个正方形都经过另一个正方形的中心
则S阴= 。
6正方形ABCD边长为12,将顶点A折
叠至DC边上的点E,使DE=5折痕为
PQ,则PQ= 。
7如图,AD平分∠BAC,DE∥AC,DF∥AB,求证:四边形AEDF是菱形
证明:∵ AD平分∠BAC∴
∴ ∠1=∠2
∵ DE∥AC
∴ ∠2=∠3
∴ ∠1=∠3
∴ AE=DE
同理可证 AF=DF
∴ 四边形AEDF是菱形
老师说小林证明有错误
(1) 请你指出他的错误,并说明理由。
(2) 请你帮小林做出正确解答。
(7) (8)
8已知∠AOB,OA=OB,点E在OB边上,四边形AEBF是矩形,请你只用无刻度的直尺在图中作出∠AOB的平分线。(保留作图痕迹)
9矩形ABCD中,AD=4,AB=10,按如图方式折叠,使点B与点D重合,折痕为EF,则DE=
10、菱形ABCD的对角线的长分别为2和5,P是对角线BD上任一点(点P不与点B、D重合),且PE∥BC交CD于E,PF∥CD交AD于F,连接EF交PD于G,则阴影部分的面积
(9) (10)
11、如图,正方形ABCD中,E是CD边中点,AC与BE交于点F,连接DF。
(1)在不增加点和线的前提下,直接写出图中所有的全等三角形;
(2)连接AE, 试判断AE与DF的位置关系,并证明你的结论;
(3)延长DF交BC于点M,试判断BM与MC得数量关系。(直接写出结论)
12、梯形ABCD中,AD∥BC,AD﹥CD,将纸片沿过点D的直线折叠,使点C落在AD上的点C′处,折痕DE交BC与点E,连接C′E。
(1)求证:四边形CDC′E是菱形;
(2)若BC=CD+AD,试判断四边形ABED的形状,并加以证明。
(11) (12)
思考题:如图①,在正方形ABCD中,点E、F分别为BC、CD的中点,AF、DE相交于点G,则有结论①AF=DE;②AF⊥DE。(不必证明)(1)如图②若点E、F不是正方形ABCD边BC、CD的中点,但满足CE=DF。则上面结论①②仍然成立吗?(请直接回答“成立|或不成立)(2)如图③若点E、F分别在正方形ABCD的边CB的延长线和边DC的延长线上,且满足CE=DF,此时上面结论①②仍然成立吗?若成立,请写出证明过程,若不成立,请说明理由;(3)如图④,在(2)的基础上,连接AE、EF,若点M、N、P、Q分别为AE、EF、FD、DA的中点,请判断四边形MNPQ是“矩形、菱形、正方形、等腰梯形中的哪一种?并写出证明过程。
特殊平行四边形答案
变式训练:
1. 邻边相等的矩形是正方形 2. 3. 1
4. B 5. 6. C 7. 12
8. 5
反馈测评:
1. 1 2. C 3. 3 4. 12
5. 4 6. 13 7. 略 8. 略
9 . 5.8 10. 11. (1) 略 (2) AE⊥DF (3) BM=CM 12. 略
思考题:⑴ 成立 ⑵ 成立 ,证明略 ⑶ 正方形,证明略
思考条
一个角90°
一组邻边相等
邻边相等
一个角90°
判定
性质
矩形四个角都是直角
矩形
菱形
矩形对角线相等
菱形四条边相等
菱形对角线互相垂直平分,且每条对角线平分一组对角。
正方形
G
F
D
C
B
A
E
1
2
B
A
C
⑸
⑸题题
C
D
A
B
P
⑷
E
⑹
C
E
B
A
D
C′
A
B
C
D
A
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
同课章节目录
