2015年秋湘教版八年级数学上册课件3.2 立方根(共14张PPT)
文档属性
| 名称 | 2015年秋湘教版八年级数学上册课件3.2 立方根(共14张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 822.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-09-22 10:48:03 | ||
图片预览



文档简介
课件14张PPT。3.2 立方根 如图1-7,一个正方体的体积为8cm3,它的棱长是多少?棱长是 cm.? 如何计算正方体的棱长呢? 正方体的体积 = 棱长×棱长×棱长 由于23=8,容易知道体积为8cm3的正方体,它的棱长为2cm. 这个例子表明,在实际问题中我们常常遇到,要找一个数,使它的立方等于给定的数.由此我们抽象出下述概念: 如果有一个数b,使得b3=a,那么我们把b叫作a的立方根. a的立方根记作 ,读作“立方根号a”或“三次根号a” 分别说出27,-27,125,-125的立方根是多少? 27的立方根是3,
-27的立方根是-3.125的立方根是5,
-125的立方根是-5. 例1 求下列各数的立方根:
1, ,0,-0.064举
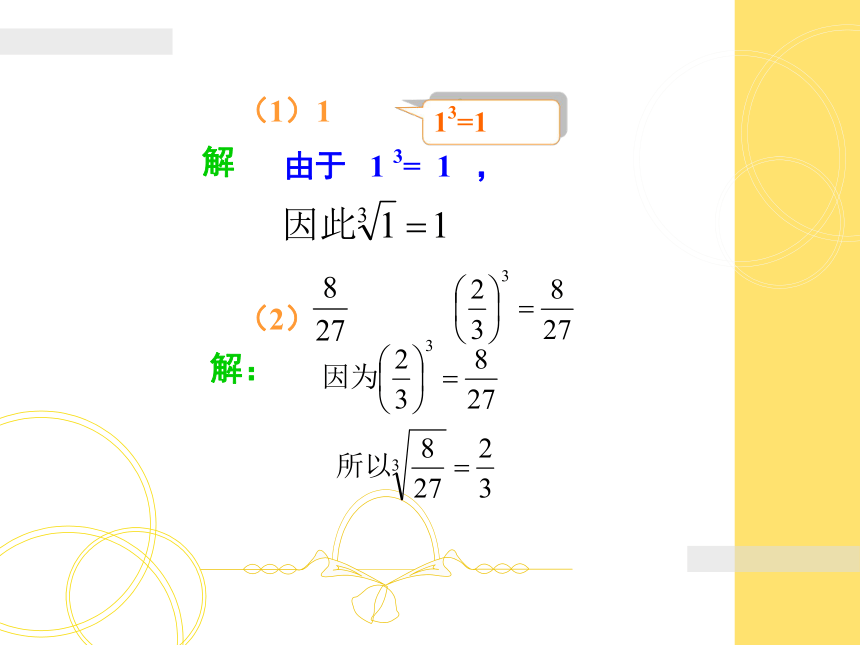
例(1)1 由于 1 3= 1 ,13=1(2) 解解:(3)0 由于 0 3= 0 ,03=0 因此 .(4)-0.064 由于 (-0.4 )3= - 0.064 ,(-0.4)3= -0.064解解1. 求下列各数的立方根:
0.064, -0.001 .3. 计算:例1 一个数的平方等于64,则这个数的立方根是 .±2例2 有下列说法: ①有理数和数轴上的点一一对应;②不带根号的数一定是有理数;③负数没有立方根;④ 是17的平方根.其中正确的有( )
A.0个 B.1个 C.2个 D.3个B例3 下列算式: ① ; ② ;③ ; ④ . 其中正确的有 ( )
A.0个 B.1个 C.2个 D.3个A
-27的立方根是-3.125的立方根是5,
-125的立方根是-5. 例1 求下列各数的立方根:
1, ,0,-0.064举
例(1)1 由于 1 3= 1 ,13=1(2) 解解:(3)0 由于 0 3= 0 ,03=0 因此 .(4)-0.064 由于 (-0.4 )3= - 0.064 ,(-0.4)3= -0.064解解1. 求下列各数的立方根:
0.064, -0.001 .3. 计算:例1 一个数的平方等于64,则这个数的立方根是 .±2例2 有下列说法: ①有理数和数轴上的点一一对应;②不带根号的数一定是有理数;③负数没有立方根;④ 是17的平方根.其中正确的有( )
A.0个 B.1个 C.2个 D.3个B例3 下列算式: ① ; ② ;③ ; ④ . 其中正确的有 ( )
A.0个 B.1个 C.2个 D.3个A
同课章节目录
