平行四边形
图片预览

文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
平行四边形
课标要求: ①掌握平行四边形的概念和性质,了解平行四边形的不稳定性。
②探索并掌握平行四边形的有关性质和平行四边形的判定条件
③探索并掌握平行四边形的重心及物理意义,了解平行四边形是中心对称图形。
复习重点 : 平行四边形的性质与判定.
考点热点: 运用平行四边形性质与判定,结合相似与全等考查对图形的理解.
归纳结构:
典例示范:
例1:如图:已知在平行四边形ABCD中,E、F是对角线BD上的两点,BE=DF,点G、H分别在BA和DC的延长线上,且AG=CH,连接GE、EH、HF、FG.
求证:四边形GEHF是平行四边形.
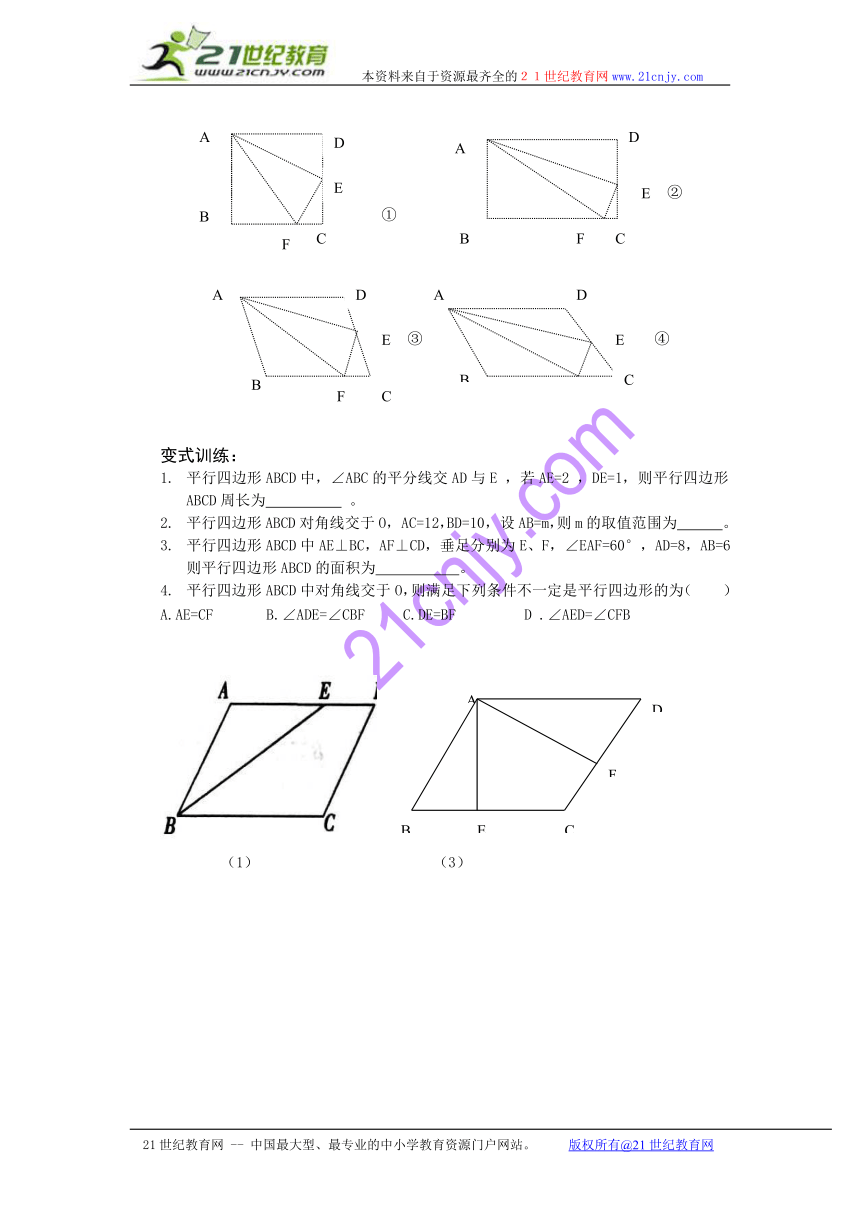
例2:如图①,小明在研究正方形ABCD的有关问题时,得出“在正方形ABCD中,如果点E是CD的中点,点F是BC边上的一点,且∠FAE=∠EAD,那么EF⊥AE”.它又将“正方形”改为“矩形”、“菱形”和“任意平行四边形”(如图②、图③、图④),其他条件不变,发现仍然有“EF⊥AE”的结论.
你同意小明的观点吗?若同意,请结合图④加以证明;若不同意,请说明理由
变式训练:
1. 平行四边形ABCD中,∠ABC的平分线交AD与E ,若AE=2 ,DE=1,则平行四边形ABCD周长为 。
2. 平行四边形ABCD对角线交于O, AC=12,BD=10, 设AB=m,则m的取值范围为 。
3. 平行四边形ABCD中AE⊥BC,AF⊥CD,垂足分别为E、F,∠EAF=60°,AD=8,AB=6则平行四边形ABCD的面积为 。
4. 平行四边形ABCD中对角线交于O,则满足下列条件不一定是平行四边形的为( )
A.AE=CF B.∠ADE=∠CBF C.DE=BF D .∠AED=∠CFB
(1) (3)
(4)
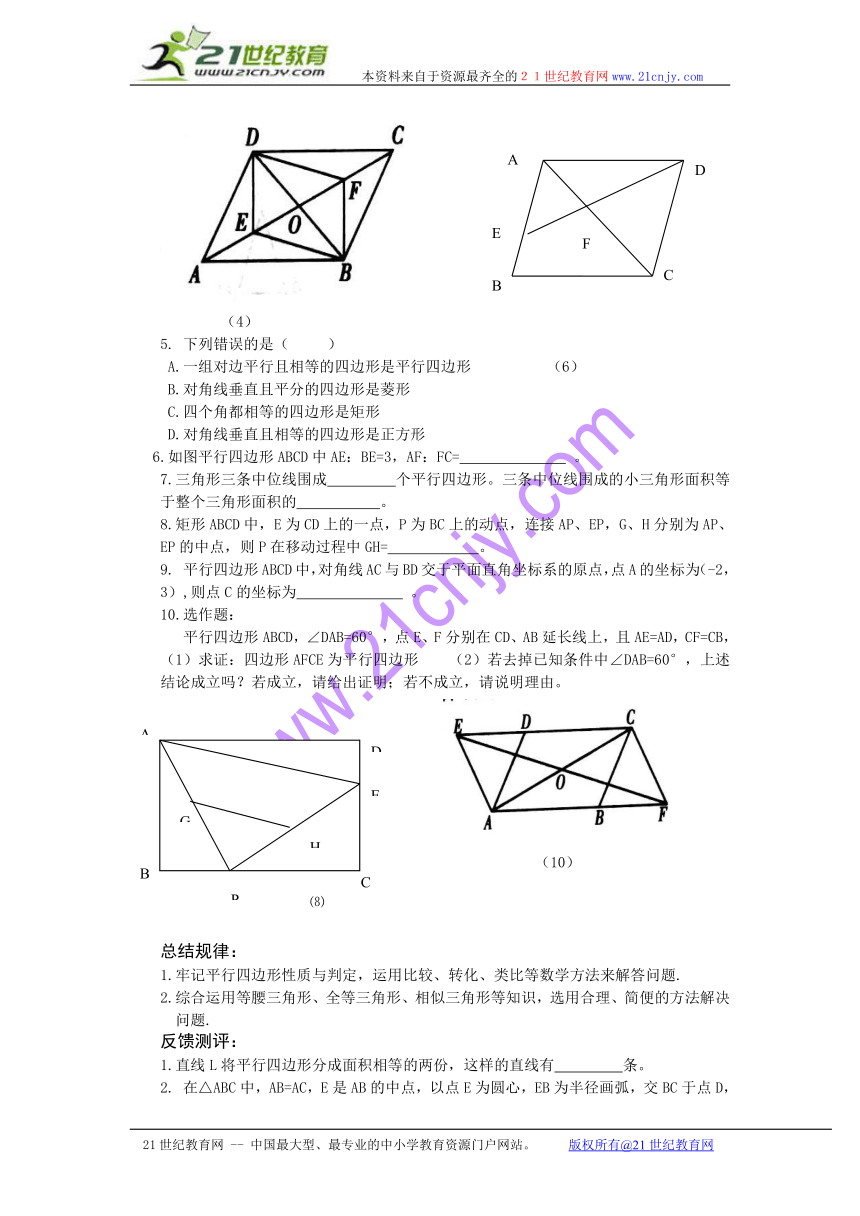
5. 下列错误的是( )
A.一组对边平行且相等的四边形是平行四边形 (6)
B.对角线垂直且平分的四边形是菱形
C.四个角都相等的四边形是矩形
D.对角线垂直且相等的四边形是正方形
6.如图平行四边形ABCD中AE:BE=3,AF:FC= 。
7.三角形三条中位线围成 个平行四边形。三条中位线围成的小三角形面积等于整个三角形面积的 。
8.矩形ABCD中,E为CD上的一点,P为BC上的动点,连接AP、EP,G、H分别为AP、EP的中点,则P在移动过程中GH= 。
9. 平行四边形ABCD中,对角线AC与BD交于平面直角坐标系的原点,点A的坐标为(-2,3),则点C的坐标为 。
10.选作题:
平行四边形ABCD,∠DAB=60°,点E、F分别在CD、AB延长线上,且AE=AD,CF=CB,(1)求证:四边形AFCE为平行四边形 (2)若去掉已知条件中∠DAB=60°,上述结论成立吗?若成立,请给出证明;若不成立,请说明理由。
(10)
总结规律:
1.牢记平行四边形性质与判定,运用比较、转化、类比等数学方法来解答问题.
2.综合运用等腰三角形、全等三角形、相似三角形等知识,选用合理、简便的方法解决问题.
反馈测评:
1.直线L将平行四边形分成面积相等的两份,这样的直线有 条。
2. 在△ABC中,AB=AC,E是AB的中点,以点E为圆心,EB为半径画弧,交BC于点D,连接ED并延长到点F,使DF=DE,连接FC,若∠B=70°,则∠F= 度。
3.已知:M是平行四边形ABCD的AB边中点,CM交BD于E,则图中阴影部分的面积与平行四边形ABCD的面积比是 。
4.平行四边形ABCD ,∠DAE=20°,∠AED=90°,则∠ B= 度;若EC:AB=1:3
AD=4,则CF=
(2) (3)
5.平行四边形ABCD,对角线相交与点O,EF过点O分别与AD 、BC交于E、F,则图中全等三角形有 对。
6.平行四边形ABCD对角线交于O ,过O作OM⊥AC,交AD与M,如果△CDM周长为a,平行四边形ABCD的周长为 。
7.点P为x轴正半轴上一个动点,过P做x轴的垂线,与双曲线y= 于点A,连接OA,并延长与双曲线的另一个交点为F, FH垂直与x轴,垂足为H,则四边形APFH的面积为 .
(5) (6) (7)
8.平行四边形ABCD-中,M、N分别是AB、CD的中点,DB分别交AN、CM与点P、Q,下列结论:
①.DP=PQ=QB;②.AP=CQ ③.CQ=2MQ
④.S△ADP=SABCD,其中正确结论是:( )
A.①②③④ B。.①②③ C. ③④ D. ①
9. 某广场有一形状为平行四边形的花坛,分别种有红、黄、蓝、绿、橙、紫六种颜色的花,如果有AB∥EF∥DC,BC∥GH∥AD,则下列错误是( )
A..红、绿花种植面积一定相等
B.紫、橙花种植面积一定相等
C.红、蓝花种植面积一定相等
D.蓝、黄花种植面积一定相等
10.平行四边形纸条ABCD中,E,F分别是边AD、BC的中点,张老师请同学将纸条
的下半部分平行四边形ABFE沿EF翻折,得到了V字形图案。
(1)请你在原图中画出 翻折后的图形ABFE
(用尺规 作图,保留 作图痕迹,不写作法。)
(2)已知∠A=63°,求∠BFC的大小。
(9) (10)
11.如图,已知直线L及L外一点A,只用圆规在直线外画出一点P,使得点A、P所在直线与直线L平行。
12.在下列直角坐标系中,(1)请写出在平行四边形内(不包括边界)横、纵坐标均为整数,且和为零的点的坐标;(2)在平行四边形内(不包括边界)任取一个横、纵坐标均为整数的点,求该点的横、纵坐标之和为零的概率。
13. 已知:任意四边形ABCD,且线段AB、BC、CD、DA、AC、BD的中点分别是E、F、F、G、H、P、Q。
(1)若四边形ABCD如图①,判断下列结论是否正确,(分别打“√”或“×”。)
甲:顺次连接EF、FG、GH、HE一定得到平行四边形.( )
乙:顺次连接EQ、QG、GP、PE一定得到平行四边形. ( )
(2)请选择甲、乙中的一个,证明你对它的判断.
(3)若四边形ABCD如图2,请判断(1)中的两个结论是否成立.
思考题:我们给出以下定义:若一个四边形的两条对角线相等,则称这个四边形为等对角线四边形。请解答下列问题:(1)写出你学过的等对角线四边形的名称。(2)探究:当等对角线四边形中两条对角线所夹锐角为60°时,这对60°角所对的两边之和与其中一条对角线的大小关系,并证明你的结论。
平行四边形答案:
变式训练:
1.10 2.1﹤m﹤11 3. 4.C
5.D 6.3:4 7.3, 8.AE
9(2,-3)
反馈测评
1.无数条 2. 40°, 1:3 3 6 4 70° 2
5. 6 6. 2a 7. 2 8. B
9. C 10. (1) 略 (2) 54° 11. 略
12.①(-1,1) (1,-1) (0,0) ② 13. (1)√ (2)√ (3) 略
思考题:⑴ 等腰梯形 矩形 正方形 ⑵ 等对角线四边形中,两条对角线所夹锐角为60°时,这对60°角所对的两边之和,大于或等于其中一条对角线长。
⑧
⑦
①
②
③
④
⑤
⑥
F
F
C
B
A
F
D
E
B
C
D
E
A
D
E
A
D
E
A
C
B
B
C
①
②
③
④
F
E
D
C
B
A
D
C
B
A
E
F
⑻
E
P
D
C
B
A
H
G
E
D
FF
C
B
A
(4)
L
.
A
E
D
C
B
A
O
F
D
E
C
B
A
F
O
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
平行四边形
课标要求: ①掌握平行四边形的概念和性质,了解平行四边形的不稳定性。
②探索并掌握平行四边形的有关性质和平行四边形的判定条件
③探索并掌握平行四边形的重心及物理意义,了解平行四边形是中心对称图形。
复习重点 : 平行四边形的性质与判定.
考点热点: 运用平行四边形性质与判定,结合相似与全等考查对图形的理解.
归纳结构:
典例示范:
例1:如图:已知在平行四边形ABCD中,E、F是对角线BD上的两点,BE=DF,点G、H分别在BA和DC的延长线上,且AG=CH,连接GE、EH、HF、FG.
求证:四边形GEHF是平行四边形.
例2:如图①,小明在研究正方形ABCD的有关问题时,得出“在正方形ABCD中,如果点E是CD的中点,点F是BC边上的一点,且∠FAE=∠EAD,那么EF⊥AE”.它又将“正方形”改为“矩形”、“菱形”和“任意平行四边形”(如图②、图③、图④),其他条件不变,发现仍然有“EF⊥AE”的结论.
你同意小明的观点吗?若同意,请结合图④加以证明;若不同意,请说明理由
变式训练:
1. 平行四边形ABCD中,∠ABC的平分线交AD与E ,若AE=2 ,DE=1,则平行四边形ABCD周长为 。
2. 平行四边形ABCD对角线交于O, AC=12,BD=10, 设AB=m,则m的取值范围为 。
3. 平行四边形ABCD中AE⊥BC,AF⊥CD,垂足分别为E、F,∠EAF=60°,AD=8,AB=6则平行四边形ABCD的面积为 。
4. 平行四边形ABCD中对角线交于O,则满足下列条件不一定是平行四边形的为( )
A.AE=CF B.∠ADE=∠CBF C.DE=BF D .∠AED=∠CFB
(1) (3)
(4)
5. 下列错误的是( )
A.一组对边平行且相等的四边形是平行四边形 (6)
B.对角线垂直且平分的四边形是菱形
C.四个角都相等的四边形是矩形
D.对角线垂直且相等的四边形是正方形
6.如图平行四边形ABCD中AE:BE=3,AF:FC= 。
7.三角形三条中位线围成 个平行四边形。三条中位线围成的小三角形面积等于整个三角形面积的 。
8.矩形ABCD中,E为CD上的一点,P为BC上的动点,连接AP、EP,G、H分别为AP、EP的中点,则P在移动过程中GH= 。
9. 平行四边形ABCD中,对角线AC与BD交于平面直角坐标系的原点,点A的坐标为(-2,3),则点C的坐标为 。
10.选作题:
平行四边形ABCD,∠DAB=60°,点E、F分别在CD、AB延长线上,且AE=AD,CF=CB,(1)求证:四边形AFCE为平行四边形 (2)若去掉已知条件中∠DAB=60°,上述结论成立吗?若成立,请给出证明;若不成立,请说明理由。
(10)
总结规律:
1.牢记平行四边形性质与判定,运用比较、转化、类比等数学方法来解答问题.
2.综合运用等腰三角形、全等三角形、相似三角形等知识,选用合理、简便的方法解决问题.
反馈测评:
1.直线L将平行四边形分成面积相等的两份,这样的直线有 条。
2. 在△ABC中,AB=AC,E是AB的中点,以点E为圆心,EB为半径画弧,交BC于点D,连接ED并延长到点F,使DF=DE,连接FC,若∠B=70°,则∠F= 度。
3.已知:M是平行四边形ABCD的AB边中点,CM交BD于E,则图中阴影部分的面积与平行四边形ABCD的面积比是 。
4.平行四边形ABCD ,∠DAE=20°,∠AED=90°,则∠ B= 度;若EC:AB=1:3
AD=4,则CF=
(2) (3)
5.平行四边形ABCD,对角线相交与点O,EF过点O分别与AD 、BC交于E、F,则图中全等三角形有 对。
6.平行四边形ABCD对角线交于O ,过O作OM⊥AC,交AD与M,如果△CDM周长为a,平行四边形ABCD的周长为 。
7.点P为x轴正半轴上一个动点,过P做x轴的垂线,与双曲线y= 于点A,连接OA,并延长与双曲线的另一个交点为F, FH垂直与x轴,垂足为H,则四边形APFH的面积为 .
(5) (6) (7)
8.平行四边形ABCD-中,M、N分别是AB、CD的中点,DB分别交AN、CM与点P、Q,下列结论:
①.DP=PQ=QB;②.AP=CQ ③.CQ=2MQ
④.S△ADP=SABCD,其中正确结论是:( )
A.①②③④ B。.①②③ C. ③④ D. ①
9. 某广场有一形状为平行四边形的花坛,分别种有红、黄、蓝、绿、橙、紫六种颜色的花,如果有AB∥EF∥DC,BC∥GH∥AD,则下列错误是( )
A..红、绿花种植面积一定相等
B.紫、橙花种植面积一定相等
C.红、蓝花种植面积一定相等
D.蓝、黄花种植面积一定相等
10.平行四边形纸条ABCD中,E,F分别是边AD、BC的中点,张老师请同学将纸条
的下半部分平行四边形ABFE沿EF翻折,得到了V字形图案。
(1)请你在原图中画出 翻折后的图形ABFE
(用尺规 作图,保留 作图痕迹,不写作法。)
(2)已知∠A=63°,求∠BFC的大小。
(9) (10)
11.如图,已知直线L及L外一点A,只用圆规在直线外画出一点P,使得点A、P所在直线与直线L平行。
12.在下列直角坐标系中,(1)请写出在平行四边形内(不包括边界)横、纵坐标均为整数,且和为零的点的坐标;(2)在平行四边形内(不包括边界)任取一个横、纵坐标均为整数的点,求该点的横、纵坐标之和为零的概率。
13. 已知:任意四边形ABCD,且线段AB、BC、CD、DA、AC、BD的中点分别是E、F、F、G、H、P、Q。
(1)若四边形ABCD如图①,判断下列结论是否正确,(分别打“√”或“×”。)
甲:顺次连接EF、FG、GH、HE一定得到平行四边形.( )
乙:顺次连接EQ、QG、GP、PE一定得到平行四边形. ( )
(2)请选择甲、乙中的一个,证明你对它的判断.
(3)若四边形ABCD如图2,请判断(1)中的两个结论是否成立.
思考题:我们给出以下定义:若一个四边形的两条对角线相等,则称这个四边形为等对角线四边形。请解答下列问题:(1)写出你学过的等对角线四边形的名称。(2)探究:当等对角线四边形中两条对角线所夹锐角为60°时,这对60°角所对的两边之和与其中一条对角线的大小关系,并证明你的结论。
平行四边形答案:
变式训练:
1.10 2.1﹤m﹤11 3. 4.C
5.D 6.3:4 7.3, 8.AE
9(2,-3)
反馈测评
1.无数条 2. 40°, 1:3 3 6 4 70° 2
5. 6 6. 2a 7. 2 8. B
9. C 10. (1) 略 (2) 54° 11. 略
12.①(-1,1) (1,-1) (0,0) ② 13. (1)√ (2)√ (3) 略
思考题:⑴ 等腰梯形 矩形 正方形 ⑵ 等对角线四边形中,两条对角线所夹锐角为60°时,这对60°角所对的两边之和,大于或等于其中一条对角线长。
⑧
⑦
①
②
③
④
⑤
⑥
F
F
C
B
A
F
D
E
B
C
D
E
A
D
E
A
D
E
A
C
B
B
C
①
②
③
④
F
E
D
C
B
A
D
C
B
A
E
F
⑻
E
P
D
C
B
A
H
G
E
D
FF
C
B
A
(4)
L
.
A
E
D
C
B
A
O
F
D
E
C
B
A
F
O
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
同课章节目录
