多边形和梯形
图片预览
文档简介
多边形和梯形
课标要求: 1. 探索并了解多边形内角和及外角和公式 ,了解正多边形概念。
2 . 探索并了解等腰梯形的性质和四边形是等腰梯形的条件。
3. 通过探索平面图形镶嵌知道任意一个三角形和四边形或正六边形可以镶嵌,并能运用这几种图形进行简单镶嵌设计。
4.了解等腰梯形 和正多边形的轴对称性及相关性质。
复习重点:与梯形相关的证明和计算。
考点热点:多边形内角和外角和,梯形的证明及计算,梯形与函数结合的题型。
归纳结构:
定义 多边形
正多边形
多边形 内角和
性质
外角和
一般梯形
梯形
特殊梯形
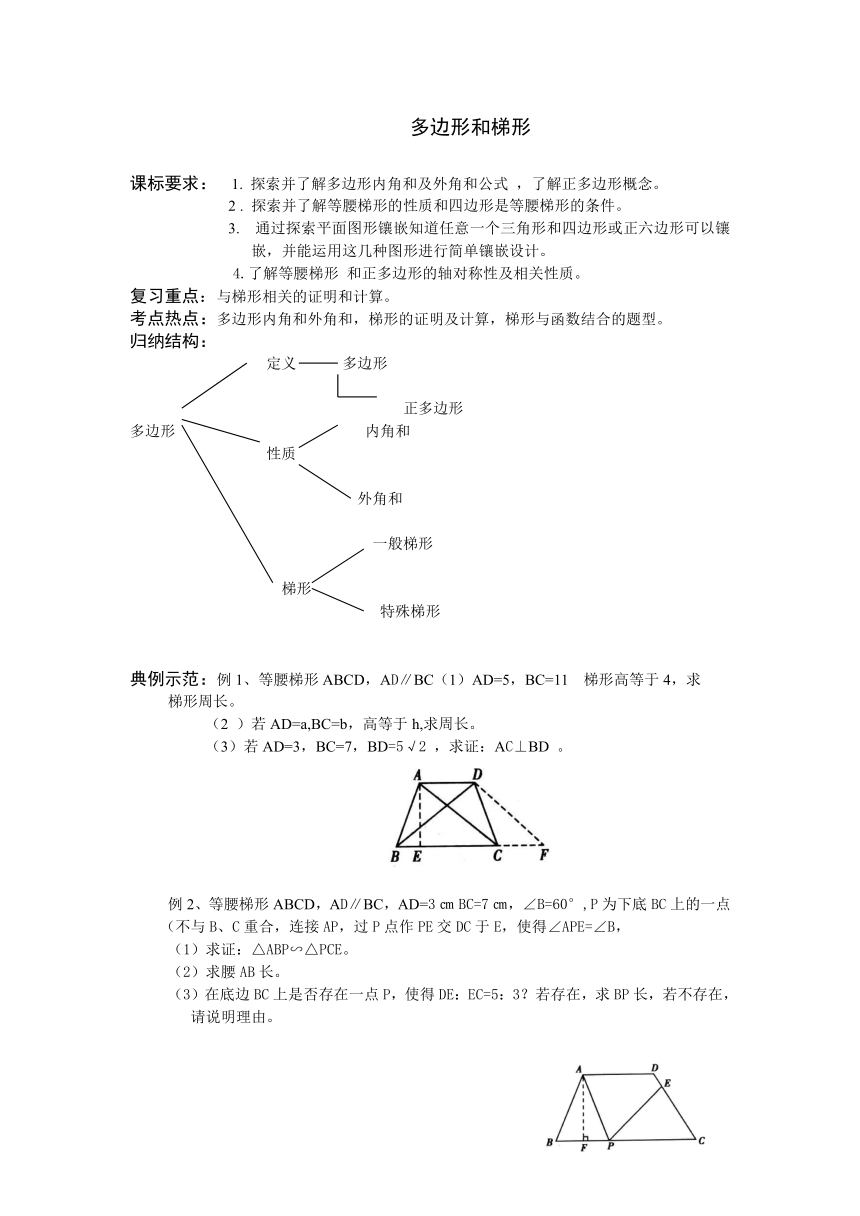
典例示范:例1、等腰梯形ABCD,AD∥BC(1)AD=5,BC=11 梯形高等于4,求
梯形周长。
(2 )若AD=a,BC=b,高等于h,求周长。
(3)若AD=3,BC=7,BD=5√2 ,求证:AC⊥BD 。
例2、等腰梯形ABCD,AD∥BC,AD=3㎝BC=7㎝,∠B=60°,P为下底BC上的一点(不与B、C重合,连接AP,过P点作PE交DC于E,使得∠APE=∠B,
(1)求证:△ABP∽△PCE。
(2)求腰AB长。
(3)在底边BC上是否存在一点P,使得DE:EC=5:3?若存在,求BP长,若不存在,请说明理由。
变式训练:
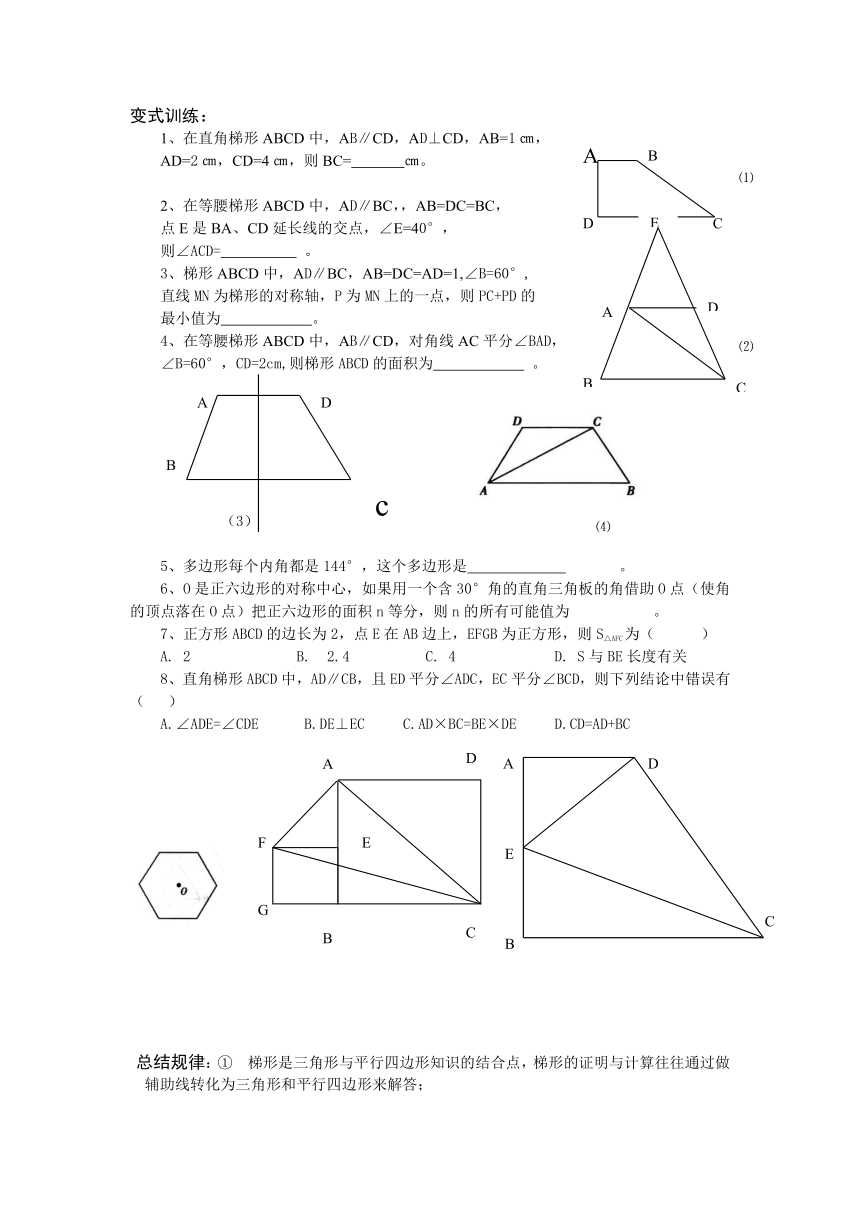
1、在直角梯形ABCD中,AB∥CD,AD⊥CD,AB=1㎝,
AD=2㎝,CD=4㎝,则BC= ㎝。
2、在等腰梯形ABCD中,AD∥BC,,AB=DC=BC,
点E是BA、CD延长线的交点,∠E=40°,
则∠ACD= 。
3、梯形ABCD中,AD∥BC,AB=DC=AD=1,∠B=60°,
直线MN为梯形的对称轴,P为MN上的一点,则PC+PD的
最小值为 。
4、在等腰梯形ABCD中,AB∥CD,对角线AC平分∠BAD,
∠B=60°,CD=2cm,则梯形ABCD的面积为 。
(3)
5、多边形每个内角都是144°,这个多边形是 。
6、O是正六边形的对称中心,如果用一个含30°角的直角三角板的角借助O点(使角的顶点落在O点)把正六边形的面积n等分,则n的所有可能值为 。
7、正方形ABCD的边长为2,点E在AB边上,EFGB为正方形,则S△AFC为( )
A. 2 B. 2.4 C. 4 D. S与BE长度有关
8、直角梯形ABCD中,AD∥CB,且ED平分∠ADC,EC平分∠BCD,则下列结论中错误有( )
A.∠ADE=∠CDE B.DE⊥EC C.AD×BC=BE×DE D.CD=AD+BC
总结规律:① 梯形是三角形与平行四边形知识的结合点,梯形的证明与计算往往通过做辅助线转化为三角形和平行四边形来解答;
② 梯形辅助线的做法;
③ 重视相似三角形、外角等知识的综合运用。
反馈测评:
1.多边形的内角和为外角和的3倍,则这个多边形为 边形。
2.如图,∠BOA=45°,过OA上到点O的距离分别是1、3、5、7、9……点作OA垂线与OB相交,得到并标出一组黑色梯形,它们的面积分别为S1、S2、S3、S4……,观察图中规律求出第10个黑色梯形面积S10= 。
3.梯形ABCD中,AD∥BC,AB=DC,且AC⊥BD,AC=6,则梯形的高DE= (不取近似值)。
4.四边形ABCD中,E、F、G、H分别为四边形个边上的中点,顺次连接EF、FG、GH、HE,则SEFGH:SABCD= 。
(3)
5.阳光中学用正三角形、正方形两种砖镶嵌地面,在每个顶点的周围正方形、正三角形地砖块数可以分别是( )
A. 2,2 B.2,3 C.1,2 D.2,1
6梯形ABCD中,AD∥BC,AB=AD=DC,点E为底边BC的中点,且DE∥AB,是判断△ADE形状,并给出证明。
7梯形ABCD中,AD∥BC,CA平分∠BCD,DE∥AC,交BC延长线与E,∠B=2∠E,①求证AB=DC;②若tanB=2, AB=,求边BC长。
(6) (7)
8小文将两个长度相等的木条AC、BD相交摆放,并使BD与AC分别与水平线的夹角∠1、∠2相等,且OD不等于OB,然后在交点处钉一钉子固定,再用一根彩带将AD、DC、CB、BA围起来,能得到一个等腰梯形吗?请说明理由。
9.梯形ABCD,AD∥BC,AB=DC=AD=6,ABC=60°,点E.F分别在线段AD.DC上,(点E不与AD重合),且∠BEF=120°,设AE=xDF=y,①求x、y函数表达式;②当x为何值时,y有最大值,并求出y的最大值。
(9) (10)
10 等腰△ABC中,AB=AC,BD⊥AC,CE⊥AB求证:四边形BCDE是等腰梯形。
11梯形ABCD中,AB∥CD,DA⊥AB,,∠B=45°延长CD到E,使DE=DA,连AE,(1)求证:AE∥BC;(2)若AB=3,CD=1,求四边形ABCE的面积。
12.直角梯形ABCD,∠B=90°,AD=3,BC=4 ,折叠梯形使点C 与点A重合,(1).求证:AECD是菱形。(2).求梯形ABCD面积
(11) (12)
梯形答案:
变式训练:
1. 2. 15° 3. 4.
5. 十 6. 12, 6,4,3,2 7. A 8. C
反馈测评:
1. 8 2. 76 3. 4. 1:2
5 B 6. 略 7.(1) 略 (2)
8 略 9.
10. 略 11. (1) 略 (2) 6 12(1). 略,(2)
C
B
A
C
B
D
E
D
A
B
A
D
E
F
G
A
B
C
D
E
A
B
C
D
E
E
D
C
F
B
A
c
A
B
C
D
B
O
A
D
C
B
A
E
⑴
⑵
⑷
⑵
⑻
课标要求: 1. 探索并了解多边形内角和及外角和公式 ,了解正多边形概念。
2 . 探索并了解等腰梯形的性质和四边形是等腰梯形的条件。
3. 通过探索平面图形镶嵌知道任意一个三角形和四边形或正六边形可以镶嵌,并能运用这几种图形进行简单镶嵌设计。
4.了解等腰梯形 和正多边形的轴对称性及相关性质。
复习重点:与梯形相关的证明和计算。
考点热点:多边形内角和外角和,梯形的证明及计算,梯形与函数结合的题型。
归纳结构:
定义 多边形
正多边形
多边形 内角和
性质
外角和
一般梯形
梯形
特殊梯形
典例示范:例1、等腰梯形ABCD,AD∥BC(1)AD=5,BC=11 梯形高等于4,求
梯形周长。
(2 )若AD=a,BC=b,高等于h,求周长。
(3)若AD=3,BC=7,BD=5√2 ,求证:AC⊥BD 。
例2、等腰梯形ABCD,AD∥BC,AD=3㎝BC=7㎝,∠B=60°,P为下底BC上的一点(不与B、C重合,连接AP,过P点作PE交DC于E,使得∠APE=∠B,
(1)求证:△ABP∽△PCE。
(2)求腰AB长。
(3)在底边BC上是否存在一点P,使得DE:EC=5:3?若存在,求BP长,若不存在,请说明理由。
变式训练:
1、在直角梯形ABCD中,AB∥CD,AD⊥CD,AB=1㎝,
AD=2㎝,CD=4㎝,则BC= ㎝。
2、在等腰梯形ABCD中,AD∥BC,,AB=DC=BC,
点E是BA、CD延长线的交点,∠E=40°,
则∠ACD= 。
3、梯形ABCD中,AD∥BC,AB=DC=AD=1,∠B=60°,
直线MN为梯形的对称轴,P为MN上的一点,则PC+PD的
最小值为 。
4、在等腰梯形ABCD中,AB∥CD,对角线AC平分∠BAD,
∠B=60°,CD=2cm,则梯形ABCD的面积为 。
(3)
5、多边形每个内角都是144°,这个多边形是 。
6、O是正六边形的对称中心,如果用一个含30°角的直角三角板的角借助O点(使角的顶点落在O点)把正六边形的面积n等分,则n的所有可能值为 。
7、正方形ABCD的边长为2,点E在AB边上,EFGB为正方形,则S△AFC为( )
A. 2 B. 2.4 C. 4 D. S与BE长度有关
8、直角梯形ABCD中,AD∥CB,且ED平分∠ADC,EC平分∠BCD,则下列结论中错误有( )
A.∠ADE=∠CDE B.DE⊥EC C.AD×BC=BE×DE D.CD=AD+BC
总结规律:① 梯形是三角形与平行四边形知识的结合点,梯形的证明与计算往往通过做辅助线转化为三角形和平行四边形来解答;
② 梯形辅助线的做法;
③ 重视相似三角形、外角等知识的综合运用。
反馈测评:
1.多边形的内角和为外角和的3倍,则这个多边形为 边形。
2.如图,∠BOA=45°,过OA上到点O的距离分别是1、3、5、7、9……点作OA垂线与OB相交,得到并标出一组黑色梯形,它们的面积分别为S1、S2、S3、S4……,观察图中规律求出第10个黑色梯形面积S10= 。
3.梯形ABCD中,AD∥BC,AB=DC,且AC⊥BD,AC=6,则梯形的高DE= (不取近似值)。
4.四边形ABCD中,E、F、G、H分别为四边形个边上的中点,顺次连接EF、FG、GH、HE,则SEFGH:SABCD= 。
(3)
5.阳光中学用正三角形、正方形两种砖镶嵌地面,在每个顶点的周围正方形、正三角形地砖块数可以分别是( )
A. 2,2 B.2,3 C.1,2 D.2,1
6梯形ABCD中,AD∥BC,AB=AD=DC,点E为底边BC的中点,且DE∥AB,是判断△ADE形状,并给出证明。
7梯形ABCD中,AD∥BC,CA平分∠BCD,DE∥AC,交BC延长线与E,∠B=2∠E,①求证AB=DC;②若tanB=2, AB=,求边BC长。
(6) (7)
8小文将两个长度相等的木条AC、BD相交摆放,并使BD与AC分别与水平线的夹角∠1、∠2相等,且OD不等于OB,然后在交点处钉一钉子固定,再用一根彩带将AD、DC、CB、BA围起来,能得到一个等腰梯形吗?请说明理由。
9.梯形ABCD,AD∥BC,AB=DC=AD=6,ABC=60°,点E.F分别在线段AD.DC上,(点E不与AD重合),且∠BEF=120°,设AE=xDF=y,①求x、y函数表达式;②当x为何值时,y有最大值,并求出y的最大值。
(9) (10)
10 等腰△ABC中,AB=AC,BD⊥AC,CE⊥AB求证:四边形BCDE是等腰梯形。
11梯形ABCD中,AB∥CD,DA⊥AB,,∠B=45°延长CD到E,使DE=DA,连AE,(1)求证:AE∥BC;(2)若AB=3,CD=1,求四边形ABCE的面积。
12.直角梯形ABCD,∠B=90°,AD=3,BC=4 ,折叠梯形使点C 与点A重合,(1).求证:AECD是菱形。(2).求梯形ABCD面积
(11) (12)
梯形答案:
变式训练:
1. 2. 15° 3. 4.
5. 十 6. 12, 6,4,3,2 7. A 8. C
反馈测评:
1. 8 2. 76 3. 4. 1:2
5 B 6. 略 7.(1) 略 (2)
8 略 9.
10. 略 11. (1) 略 (2) 6 12(1). 略,(2)
C
B
A
C
B
D
E
D
A
B
A
D
E
F
G
A
B
C
D
E
A
B
C
D
E
E
D
C
F
B
A
c
A
B
C
D
B
O
A
D
C
B
A
E
⑴
⑵
⑷
⑵
⑻
同课章节目录
