三角形(一)
图片预览

文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
三角形(一)
一、课标要求
1、了解三角形有关概念,会画出任意三角形的角平分线、中线和高,了解三角形的稳定性。
2、探索并掌握三角形中位线的性质。
3、了解等腰三角形的有关概念,探索并掌握等腰三角形的性质和一个三角形是等腰三角形的条件,了解等边三角形的概念并探索其性质。
4、了解直角三角形的概念,探索并掌握直角三角形的性质和一个三角形是直角三角形的条件。
5、体验勾股定理的探索过程,会运用勾股定理解决简单问题,会用勾股定理的逆定理判定直角三角形。
二、复习重点
1、等腰等边三角形的性质和判定。
2、直角三角形的性质和判定。
3、勾股定理的运用。
三、知识结构
主要线段:角平分线、中线、高线、中位线
边:两边之和大于第三边;两边之差小于第三边
性质
三角形 角:内角和为180°、 一个外角大于不相邻两个内角和
等腰三角形 等边三角形(三线和一)
勾股定理
特殊三角形
30°角所对的直角边等于斜边的一半
直角三角形
两锐角互余
斜边上的中线等于斜边的一半
四、考点热点
1、三角形的分类。 2、三角形的边角关系。 3、三角形中线、角平分线、高线。
4、三角形的中位线。 5、等腰三角形 6、等边三角形 7、直角三角形
五、典例示范
1、三角形两边的长分别是8和6,第三边的长是一元二次方程x-16x+60=0的一个实数根,则该三角形的面积是 ( )
A.24 B.24或8 C.48 D. 8
2、等腰三角形两边长分别是2㎝和5㎝,则这个三角形周长是( )
A.9㎝ B.12㎝ C. 9㎝ 或12㎝ D.14㎝
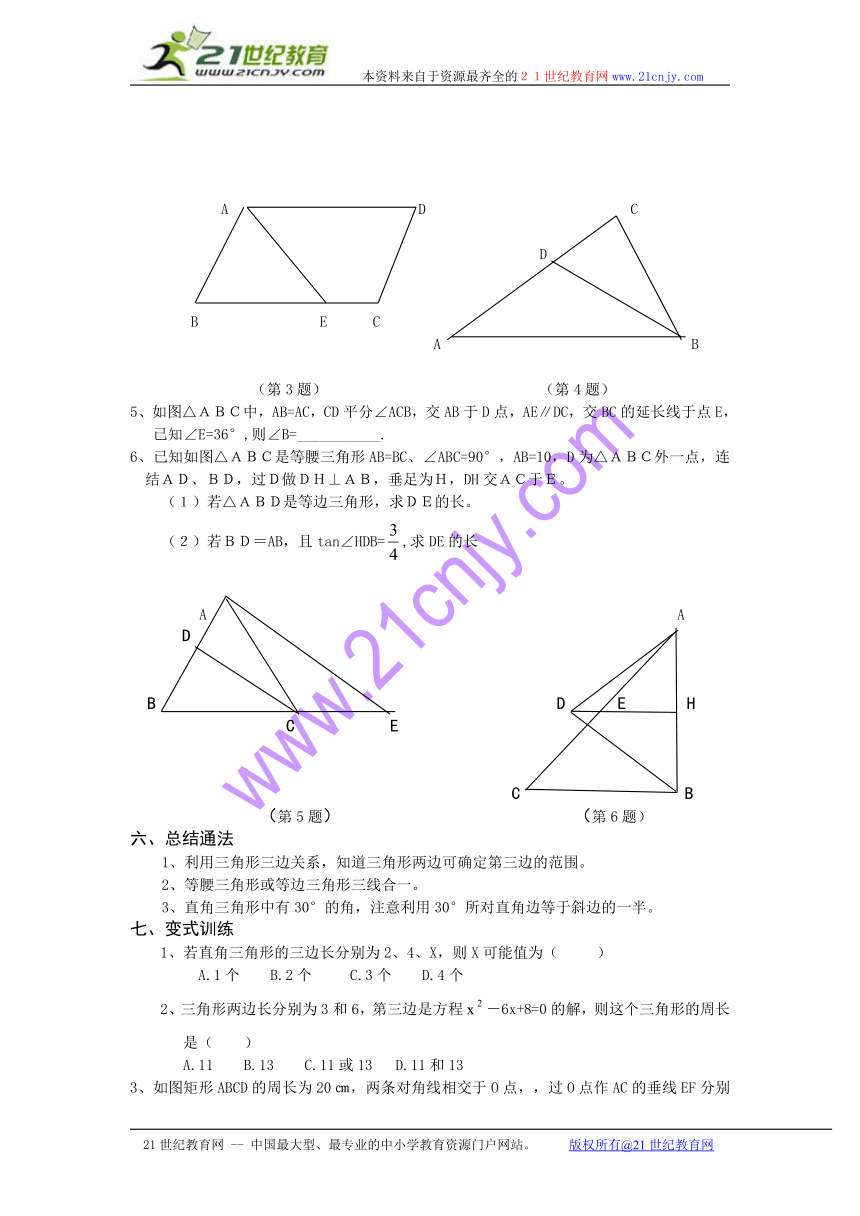
3、如图在平行四边形ABCD中,已知AD=5cm,AB=3cm ,AE平分∠BAD交 BC边于点E、则EC等于 ( )
A.1cm B.2cm C.3cm D.4cm
4、如图△ABC中,∠C=90°,∠ABC=60°,BD平分∠ABC,若AD=6,则CD=______.
A D C
D
B E C
A B
(第3题) (第4题)
5、如图△ABC中,AB=AC,CD平分∠ACB,交AB于D点,AE∥DC,交BC的延长线于点E,已知∠E=36°,则∠B=___________.
6、已知如图△ABC是等腰三角形AB=BC、∠ABC=90°,AB=10,D为△ABC外一点,连结AD、BD,过D做DH⊥AB,垂足为H,DH交AC于E。
(1)若△ABD是等边三角形,求DE的长。
(2)若BD=AB,且tan∠HDB=,求DE的长
A A
D
B D E H
C E
C B
(第5题) (第6题)
六、总结通法
1、利用三角形三边关系,知道三角形两边可确定第三边的范围。
2、等腰三角形或等边三角形三线合一。
3、直角三角形中有30°的角,注意利用30°所对直角边等于斜边的一半。
七、变式训练
1、若直角三角形的三边长分别为2、4、X,则X可能值为( )
A.1个 B.2个 C.3个 D.4个
2、三角形两边长分别为3和6,第三边是方程x-6x+8=0的解,则这个三角形的周长是( )
A.11 B.13 C.11或13 D.11和13
3、如图矩形ABCD的周长为20㎝,两条对角线相交于O点,,过O点作AC的垂线EF分别交AD、BC与E、F点,连结CE,则△CDE的周长为( )
A.5㎝ B.8㎝ C.9㎝ D.10㎝
A
A E D
O
E
B F C B C
D
(第3题) (第4题)
4、如图△ABC中,BC=AC,∠C=90°,AD是△ABC的角平分线,DE⊥AB,垂足为E,已知CD=4㎝,则AC=___㎝.
5、等腰三角形腰上的高是腰长的一半,则这个等腰三角形底角为______.
6、如图将纸片ABC沿DE折叠点A落在A‵处,已知∠1+∠2=100°则∠A =____
A
D E
α
1 2
A‵
B C
(第6题) (第7题)
7、如图把一副三角尺叠放在一起,∠α的度数是______.
8、如图点O是等边三角形内一点,∠AOB=110°,∠BOC=α,将△BOC绕点C按顺时针方向旋转60度,得△ADC,连结OD。
(1)求证△COD是等边三角形。
(2)当∠α=150度,试判断△AOD的形状,并说明理由。
(3)探究当α为多少度时△AOD是等腰三角形。
A
D
110° O
α
B C
(第8题)
八、反馈测试
1、小芳要画一个有两边长分别为5㎝和6㎝的等腰三角形,则这个等腰三角形的周长是( )
A.16㎝ B.17㎝ C.16㎝或17㎝ D.11㎝
2、如图在等腰三角形ABC中,AB=AC,∠A=44°,CD⊥AB于D,则∠DCB=( )
A. 44° B.68° C. 46° D. 22°
A C′
A D
D
B C
B C E
(第2题) (第3题)
3、将一张矩形纸片ABCD如图折起来,使定点C落在C处,其中AB=4,若∠CED=30°,则折痕ED的长为( )
A.4 B.4 C.8 D. 5
4、如图将一个等腰直角三角形按图示方式依次翻折,若DE=a,则①DC‵平分∠BDE。②BC长为(+2)a ③△BCD是等腰三角形 ④△CED的周长等于BC的长,其中正确的有( ) A.1个 B.2个 C.3个 D.4个
A A
D D
B C B E C B C′ E C
(第4题)
5、如图在梯形ABCD中,AD∥BC,BC=BD,AB=AD,∠A=120°,则∠C=_________°
A D A
E
B C
C D B
(第5题) (第6题)
6、如图在三角形ABC中,AC=BC=2, ∠ACB=90°,D是BC边上的中点,点E是AB上的一动点,则EC+ED的最小值是 _________
7、如图在三角形ABC中,BC=5㎝,BP、CP分别是∠ACB和∠ABC的角平分线,且PD∥AB,PE∥AC,则△PDE的周长是_________㎝.
A A
D
P
B D E C B C E
(第7题) (第8题)
8、如图在三角形ABC中,BD平分∠ABC,CD平分∠ACE,请你写出∠A与∠D的关系是__________.
9、将一根25㎝的细木棒放入长、宽、高分别为8㎝、6㎝、和10㎝的长方体无盖盒子中,则细木棒露在盒外面的最短长度是___________________.
10、如图在三角形ABC中,∠C=2∠B,D是BC上的一点,且AD⊥AB,点E是BD的中点,连结AE。
(1)求证∠AEC=∠C
(2)求证BD=2AC
(3)若AE=6.5,AD=5,求三角形ABE的周长。
A
B E D C
(第10题)
参考答案 1C 2D 3C 4B 5、 75° 6、+1 7、5 8 ∠A=2∠D 9、5cm
10①证明∵AE=BE ∴∠AEC=2∠B 又∵∠C=2∠B ∴∠AEC=∠C
②证明∵△ABD是直角三角形、E是BD的中点∴BD=2AE 又∵∠AEC=∠C
∴AE=AC ∴BD=2AC
③ 30
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
三角形(一)
一、课标要求
1、了解三角形有关概念,会画出任意三角形的角平分线、中线和高,了解三角形的稳定性。
2、探索并掌握三角形中位线的性质。
3、了解等腰三角形的有关概念,探索并掌握等腰三角形的性质和一个三角形是等腰三角形的条件,了解等边三角形的概念并探索其性质。
4、了解直角三角形的概念,探索并掌握直角三角形的性质和一个三角形是直角三角形的条件。
5、体验勾股定理的探索过程,会运用勾股定理解决简单问题,会用勾股定理的逆定理判定直角三角形。
二、复习重点
1、等腰等边三角形的性质和判定。
2、直角三角形的性质和判定。
3、勾股定理的运用。
三、知识结构
主要线段:角平分线、中线、高线、中位线
边:两边之和大于第三边;两边之差小于第三边
性质
三角形 角:内角和为180°、 一个外角大于不相邻两个内角和
等腰三角形 等边三角形(三线和一)
勾股定理
特殊三角形
30°角所对的直角边等于斜边的一半
直角三角形
两锐角互余
斜边上的中线等于斜边的一半
四、考点热点
1、三角形的分类。 2、三角形的边角关系。 3、三角形中线、角平分线、高线。
4、三角形的中位线。 5、等腰三角形 6、等边三角形 7、直角三角形
五、典例示范
1、三角形两边的长分别是8和6,第三边的长是一元二次方程x-16x+60=0的一个实数根,则该三角形的面积是 ( )
A.24 B.24或8 C.48 D. 8
2、等腰三角形两边长分别是2㎝和5㎝,则这个三角形周长是( )
A.9㎝ B.12㎝ C. 9㎝ 或12㎝ D.14㎝
3、如图在平行四边形ABCD中,已知AD=5cm,AB=3cm ,AE平分∠BAD交 BC边于点E、则EC等于 ( )
A.1cm B.2cm C.3cm D.4cm
4、如图△ABC中,∠C=90°,∠ABC=60°,BD平分∠ABC,若AD=6,则CD=______.
A D C
D
B E C
A B
(第3题) (第4题)
5、如图△ABC中,AB=AC,CD平分∠ACB,交AB于D点,AE∥DC,交BC的延长线于点E,已知∠E=36°,则∠B=___________.
6、已知如图△ABC是等腰三角形AB=BC、∠ABC=90°,AB=10,D为△ABC外一点,连结AD、BD,过D做DH⊥AB,垂足为H,DH交AC于E。
(1)若△ABD是等边三角形,求DE的长。
(2)若BD=AB,且tan∠HDB=,求DE的长
A A
D
B D E H
C E
C B
(第5题) (第6题)
六、总结通法
1、利用三角形三边关系,知道三角形两边可确定第三边的范围。
2、等腰三角形或等边三角形三线合一。
3、直角三角形中有30°的角,注意利用30°所对直角边等于斜边的一半。
七、变式训练
1、若直角三角形的三边长分别为2、4、X,则X可能值为( )
A.1个 B.2个 C.3个 D.4个
2、三角形两边长分别为3和6,第三边是方程x-6x+8=0的解,则这个三角形的周长是( )
A.11 B.13 C.11或13 D.11和13
3、如图矩形ABCD的周长为20㎝,两条对角线相交于O点,,过O点作AC的垂线EF分别交AD、BC与E、F点,连结CE,则△CDE的周长为( )
A.5㎝ B.8㎝ C.9㎝ D.10㎝
A
A E D
O
E
B F C B C
D
(第3题) (第4题)
4、如图△ABC中,BC=AC,∠C=90°,AD是△ABC的角平分线,DE⊥AB,垂足为E,已知CD=4㎝,则AC=___㎝.
5、等腰三角形腰上的高是腰长的一半,则这个等腰三角形底角为______.
6、如图将纸片ABC沿DE折叠点A落在A‵处,已知∠1+∠2=100°则∠A =____
A
D E
α
1 2
A‵
B C
(第6题) (第7题)
7、如图把一副三角尺叠放在一起,∠α的度数是______.
8、如图点O是等边三角形内一点,∠AOB=110°,∠BOC=α,将△BOC绕点C按顺时针方向旋转60度,得△ADC,连结OD。
(1)求证△COD是等边三角形。
(2)当∠α=150度,试判断△AOD的形状,并说明理由。
(3)探究当α为多少度时△AOD是等腰三角形。
A
D
110° O
α
B C
(第8题)
八、反馈测试
1、小芳要画一个有两边长分别为5㎝和6㎝的等腰三角形,则这个等腰三角形的周长是( )
A.16㎝ B.17㎝ C.16㎝或17㎝ D.11㎝
2、如图在等腰三角形ABC中,AB=AC,∠A=44°,CD⊥AB于D,则∠DCB=( )
A. 44° B.68° C. 46° D. 22°
A C′
A D
D
B C
B C E
(第2题) (第3题)
3、将一张矩形纸片ABCD如图折起来,使定点C落在C处,其中AB=4,若∠CED=30°,则折痕ED的长为( )
A.4 B.4 C.8 D. 5
4、如图将一个等腰直角三角形按图示方式依次翻折,若DE=a,则①DC‵平分∠BDE。②BC长为(+2)a ③△BCD是等腰三角形 ④△CED的周长等于BC的长,其中正确的有( ) A.1个 B.2个 C.3个 D.4个
A A
D D
B C B E C B C′ E C
(第4题)
5、如图在梯形ABCD中,AD∥BC,BC=BD,AB=AD,∠A=120°,则∠C=_________°
A D A
E
B C
C D B
(第5题) (第6题)
6、如图在三角形ABC中,AC=BC=2, ∠ACB=90°,D是BC边上的中点,点E是AB上的一动点,则EC+ED的最小值是 _________
7、如图在三角形ABC中,BC=5㎝,BP、CP分别是∠ACB和∠ABC的角平分线,且PD∥AB,PE∥AC,则△PDE的周长是_________㎝.
A A
D
P
B D E C B C E
(第7题) (第8题)
8、如图在三角形ABC中,BD平分∠ABC,CD平分∠ACE,请你写出∠A与∠D的关系是__________.
9、将一根25㎝的细木棒放入长、宽、高分别为8㎝、6㎝、和10㎝的长方体无盖盒子中,则细木棒露在盒外面的最短长度是___________________.
10、如图在三角形ABC中,∠C=2∠B,D是BC上的一点,且AD⊥AB,点E是BD的中点,连结AE。
(1)求证∠AEC=∠C
(2)求证BD=2AC
(3)若AE=6.5,AD=5,求三角形ABE的周长。
A
B E D C
(第10题)
参考答案 1C 2D 3C 4B 5、 75° 6、+1 7、5 8 ∠A=2∠D 9、5cm
10①证明∵AE=BE ∴∠AEC=2∠B 又∵∠C=2∠B ∴∠AEC=∠C
②证明∵△ABD是直角三角形、E是BD的中点∴BD=2AE 又∵∠AEC=∠C
∴AE=AC ∴BD=2AC
③ 30
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
同课章节目录
