四年级下册数学人教版三角形的内角和课件(共19张PPT)
文档属性
| 名称 | 四年级下册数学人教版三角形的内角和课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-24 07:38:26 | ||
图片预览



文档简介
(共19张PPT)
三角形的内角和
R·四年级下册
第五单元 三角形
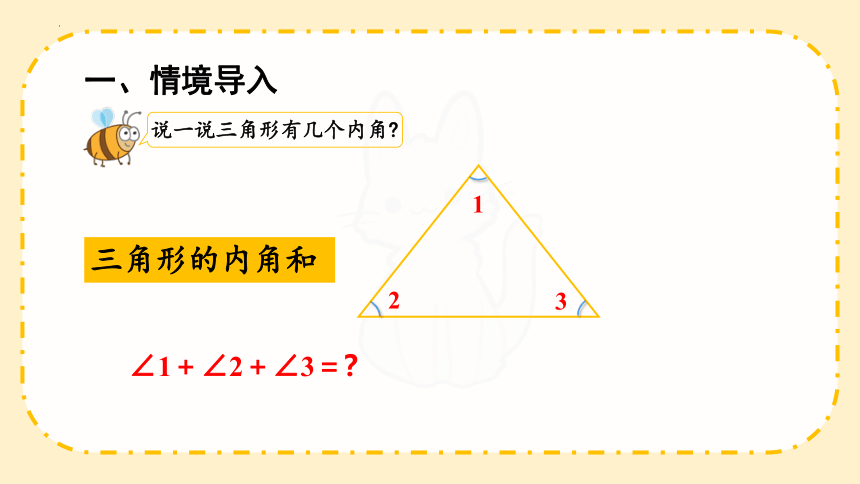
一、情境导入
说一说三角形有几个内角
1
2
3
∠1+∠2+∠3=?
三角形的内角和
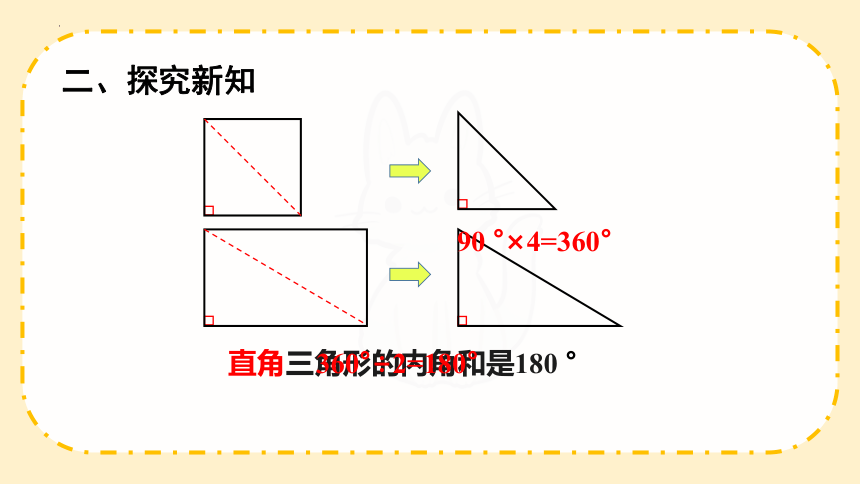
二、探究新知
直角三角形的内角和是180 °
90 °×4=360°
360°÷2=180°
思考:是不是任意三角形的内角和都是180°呢?
一起来探究任意三角形的内角和
画几个不同类型的三角形。量一量,算一算,三角形的3个内角的和各是多少度。
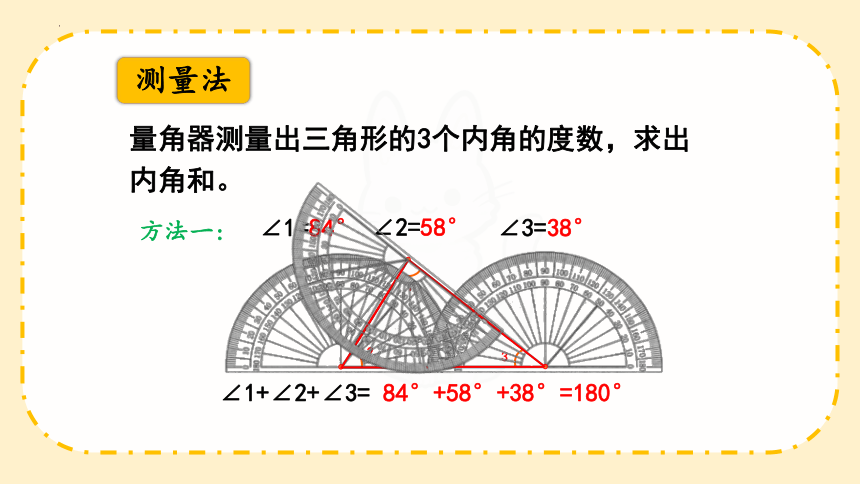
测量法
量角器测量出三角形的3个内角的度数,求出内角和。
2
1
3
∠1+∠2+∠3= 84°+58°+38°=180°
方法一:
∠1=84°
∠2=58°
∠3=38°
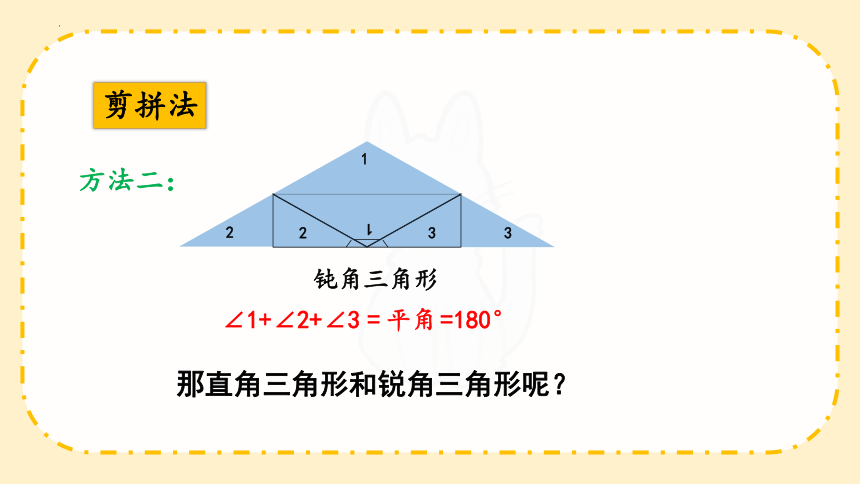
剪拼法
1
2
2
3
3
钝角三角形
1
∠1+∠2+∠3
=
平角
=180°
方法二:
那直角三角形和锐角三角形呢?
折一折
2
2
1
1
3
3
折成了一个平角。
转化法
1
4
2
3
1
4
2
3
三角形的内角和是180度。
三、巩固练习
1.在右图中, ∠1=140°,
∠3=25°。求∠2的度数。
答: ∠2的度数是15°。
180 °-(140°+25°)=
15°
2.把下面这个三角形沿虚线剪成两个小三角形,每个小三角形的内角和是多少度
因为:三角形的内角和是180°,
所以:这个三角形沿虚线剪成两个小三角形,
每个小三角形的内角和也是180°。
3.判断题
(1)锐角三角形的内角和小于直角三角形的内角和。
( )
(3)等腰三角形都是锐角三角形。 ( )
(4)等腰三角形都是等边三角形。 ( )
×
×
×
(2)三角形内角和等于180度。 ( )
√
180°-65°-37°
=78°
180°-90°-30°
=60°
180°-20°-25°
=135°
4.算出下面各个未知角的度数。
【选自教材P67 练习十六 第1题】
5.求出下列三角形各个角的度数。
(1)一个等边三角形。
(2)一个等腰三角形,顶角是96°。
(3)一个直角三角形,其中一个锐角是40°。
每个角都是60°。
顶角是96°,两个底角都是(180° - 96°)÷2=42°。
一个锐角是40°,另一个锐角是90°-40°=50°,还有一个角是90°。
【选自教材P67 练习十六 第2题】
∠A=180°-75°-60°=45°
6.在三角形ABC 中,如果∠B =75°,∠C =60°,那么∠A 是多少度?
1.填空。
(1)三角形的内角和是( )。
(2)一个三角形中,一个角是80°,另一个角是50°,第三个角是( )°, 按边分,这是一个( )三角形。
180°
50
等腰
备选练习
(3)等边三角形的三个内角都是( )°。
60
四、课堂总结
同学们,这节课你们都学会了哪些知识?
任意三角形的内角和是180°。
测量法
剪拼法
折一折
转化法
六、作业布置
完成相关练习
三角形的内角和
R·四年级下册
第五单元 三角形
一、情境导入
说一说三角形有几个内角
1
2
3
∠1+∠2+∠3=?
三角形的内角和
二、探究新知
直角三角形的内角和是180 °
90 °×4=360°
360°÷2=180°
思考:是不是任意三角形的内角和都是180°呢?
一起来探究任意三角形的内角和
画几个不同类型的三角形。量一量,算一算,三角形的3个内角的和各是多少度。
测量法
量角器测量出三角形的3个内角的度数,求出内角和。
2
1
3
∠1+∠2+∠3= 84°+58°+38°=180°
方法一:
∠1=84°
∠2=58°
∠3=38°
剪拼法
1
2
2
3
3
钝角三角形
1
∠1+∠2+∠3
=
平角
=180°
方法二:
那直角三角形和锐角三角形呢?
折一折
2
2
1
1
3
3
折成了一个平角。
转化法
1
4
2
3
1
4
2
3
三角形的内角和是180度。
三、巩固练习
1.在右图中, ∠1=140°,
∠3=25°。求∠2的度数。
答: ∠2的度数是15°。
180 °-(140°+25°)=
15°
2.把下面这个三角形沿虚线剪成两个小三角形,每个小三角形的内角和是多少度
因为:三角形的内角和是180°,
所以:这个三角形沿虚线剪成两个小三角形,
每个小三角形的内角和也是180°。
3.判断题
(1)锐角三角形的内角和小于直角三角形的内角和。
( )
(3)等腰三角形都是锐角三角形。 ( )
(4)等腰三角形都是等边三角形。 ( )
×
×
×
(2)三角形内角和等于180度。 ( )
√
180°-65°-37°
=78°
180°-90°-30°
=60°
180°-20°-25°
=135°
4.算出下面各个未知角的度数。
【选自教材P67 练习十六 第1题】
5.求出下列三角形各个角的度数。
(1)一个等边三角形。
(2)一个等腰三角形,顶角是96°。
(3)一个直角三角形,其中一个锐角是40°。
每个角都是60°。
顶角是96°,两个底角都是(180° - 96°)÷2=42°。
一个锐角是40°,另一个锐角是90°-40°=50°,还有一个角是90°。
【选自教材P67 练习十六 第2题】
∠A=180°-75°-60°=45°
6.在三角形ABC 中,如果∠B =75°,∠C =60°,那么∠A 是多少度?
1.填空。
(1)三角形的内角和是( )。
(2)一个三角形中,一个角是80°,另一个角是50°,第三个角是( )°, 按边分,这是一个( )三角形。
180°
50
等腰
备选练习
(3)等边三角形的三个内角都是( )°。
60
四、课堂总结
同学们,这节课你们都学会了哪些知识?
任意三角形的内角和是180°。
测量法
剪拼法
折一折
转化法
六、作业布置
完成相关练习
